【机器学习】无监督学习

机器学习

Scikit-learn
- 无监督学习
- - 无监督学习概念
  - 聚类算法
  - - [聚类基础与 K-Means](#聚类基础与 K-Means)
    - [层次聚类（Hierarchical Clustering）](#层次聚类（Hierarchical Clustering）)
    - [DBSCAN 与密度聚类](#DBSCAN 与密度聚类)
  - 降维算法
  - - PCA（主成分分析）
    - [LDA（有监督）与 t-SNE（非线性）](#LDA（有监督）与 t-SNE（非线性）)
  - 案例：客户分群

Scikit-learn

无监督学习

无监督学习概念

无监督学习的核心定义

无监督学习（Unsupervised Learning）是机器学习的三大核心范式之一（另外两种是监督学习和强化学习），其核心思想可以用一句话概括：

"用没有标签的样本训练模型，让模型自动从数据中发现潜在的结构、规律或分组，而不需要人工提供'标准答案'。"

这里的 "无监督" 可以理解为：模型在学习过程中没有 "老师指导"（没有标签），只能靠自己 "观察数据"------ 就像给孩子一堆不同形状的积木，孩子不需要知道 "这是三角形、那是正方形"，就能自己按形状、大小分成几堆，这个 "自主分类" 的过程就是无监督学习的本质。

无监督学习与监督学习的核心区别

最关键的差异在于是否有 "标签（y）"，这直接决定了模型的学习目标和流程：

对比维度	监督学习（Supervised Learning）	无监督学习（Unsupervised Learning）
核心输入	特征（X）+ 标签（y，已知答案）	只有特征（X），无标签（y，无答案）
学习目标	学习 "X→y" 的映射关系，用于预测新样本的标签	从 X 中挖掘隐藏结构（如分组、规律、压缩特征）
典型任务	分类（预测离散类别）、回归（预测连续数值）	聚类（分组）、降维（压缩特征）、异常检测
类比场景	做有答案的练习题（已知对错，总结解题规律）	玩积木（无说明书，自己摸索分类 / 搭建规律）
核心产出	能预测标签的 "预测模型"	能发现数据规律的 "分析模型"（如聚类结果、降维特征）

举个具体例子：

监督学习场景：给 1000 张猫 / 狗图片（每张都标了 "猫" 或 "狗"），训练模型区分新图片是猫还是狗；
无监督学习场景：给 1000 张动物图片（没标任何类别），让模型自己把 "看起来像的" 分成几堆（可能正好分成猫、狗、鸟等组）。

无监督学习的两大核心任务

无监督学习不直接做 "预测"，而是聚焦于 "数据探索" 和 "特征处理"，主要分为两大核心任务：聚类（Clustering） 和 降维（Dimensionality Reduction），此外还有异常检测、关联规则挖掘等延伸任务。

任务类型	核心目标	通俗理解	生活案例
聚类（Clustering）	将相似的样本自动归为一类，不相似的样本分在不同类	"物以类聚，人以群分"	电商自动给用户分群（如 "高频消费用户""偶尔浏览用户"）、新闻按主题分类（如 "体育""科技"）
降维（Dimensionality Reduction）	在保留数据核心信息的前提下，减少特征的维度	"压缩数据，保留精华"	把 100 个特征的用户数据压缩到 2 个维度，方便画图展示；把高清图片压缩成小尺寸，减少存储
异常检测（Anomaly Detection）	从数据中识别出 "与众不同" 的异常样本	"找出不合群的样本"	信用卡交易中的异常消费（如突然在国外大额消费）、工厂设备传感器的异常数据（预示故障）

无监督学习的典型应用场景

无监督学习在 "缺乏标签" 或 "需要探索数据" 的场景中至关重要，常见应用包括：

数据探索与分析：拿到新数据集时，先用聚类看是否有自然分组，用降维可视化数据分布（比如 "用户行为数据是否能分成几类？"）；
特征工程预处理：用降维（如 PCA）压缩高维特征（比如把 100 个用户行为特征压缩到 10 个），减少模型计算量，避免 "维度灾难"；
商业决策支持：电商客户分群（针对不同群体设计营销策略）、推荐系统（给 "相似兴趣" 的用户推同类商品）；
异常监控：金融欺诈检测（异常交易）、工业设备故障预警（异常传感器数据）。

无监督学习的核心挑战

相比监督学习，无监督学习的 "不确定性" 更强，主要有两个核心挑战：

无客观评估标准：没有标签（y），无法像监督学习那样用 "准确率、RMSE" 等指标直接判断结果好坏 ------ 比如聚类把数据分成 3 堆还是 4 堆，没有 "标准答案"，只能靠业务经验或轮廓系数等间接指标评估；
结果需结合业务解读：模型输出的 "规律" 需要人来解读 ------ 比如聚类分出 "用户群 A" 和 "用户群 B"，需要业务人员进一步分析 "群 A 是年轻人、群 B 是中年人"，才能落地使用。

聚类算法

聚类基础与 K-Means

聚类（Clustering）：无监督学习的 "分组术"

在学 K-Means 之前，先明确 "聚类" 的核心概念：

聚类是无监督学习的核心任务 ，目标是让算法在没有标签的情况下，根据数据自身的 "相似性"（如距离、特征相似度），自动将样本分成若干个 "簇（Cluster）"------ 同一簇的样本尽可能相似，不同簇的样本尽可能不同。

简单说，就是让数据 "物以类聚"：比如把一堆水果按 "大小 + 颜色" 自动分成 "苹果、香蕉、橙子" 三组，把用户按 "消费频率 + 消费金额" 自动分成 "高价值用户、普通用户、低活跃用户"。

聚类的核心应用场景

聚类在实际业务中用途极广，常见场景包括：

客户分群：电商按用户购买行为分群，针对性推送优惠券（如给高频高客单价用户推奢侈品，给低频用户推满减券）；
内容分类：新闻 APP 按文章关键词自动分 "体育、科技、娱乐" 板块，短视频平台按用户观看偏好分兴趣组；
图像分割：医学影像中自动把 "肿瘤区域" 和 "正常组织" 分成不同簇，辅助医生诊断；
异常检测：信用卡交易中，把 "大额异地消费" 等与正常交易差异大的样本归为 "孤立簇"，识别欺诈行为；
数据预处理：聚类后用 "簇中心" 代替原始样本，压缩数据量（比如把 10 万用户聚成 100 个簇，用簇中心代表该组用户特征）。

K-Means 算法：最经典的 "中心聚类法"

K-Means 是聚类算法里的 "入门首选"，核心思想简单直观 ------ 通过迭代找到 k 个簇中心，让所有样本都 "归属于离自己最近的簇中心"，最终实现 "簇内样本相似度高，簇间样本相似度低"。

K-Means 核心原理（3 步迭代法）

K-Means 的逻辑可以拆解为 "初始化→分配→更新" 三个步骤，循环执行直到簇中心稳定（收敛）：

初始化簇中心
从所有样本中随机选择 k 个样本 ，作为初始的 "簇中心"（k 是我们需要提前指定的 "簇的数量"，比如要分 3 组就选 3 个中心）。
例：从 100 个用户样本中随机选 3 个，作为 "高价值、普通、低活跃" 的初始中心。
分配样本到簇
计算每个样本到 k 个簇中心的距离 （常用 "欧氏距离"，即两点间直线距离），把样本分配到 "距离最近的簇中心" 所在的簇。
例：用户 A 到 "高价值中心" 距离最近，就把 A 归为 "高价值簇"；用户 B 到 "普通中心" 最近，归为 "普通簇"。
更新簇中心
所有样本分配完成后，计算每个簇内所有样本的 "均值"（比如每个特征的平均值），用这个均值作为新的簇中心 （替代原来的中心）。
例："高价值簇" 内所有用户的 "平均消费金额、平均消费频率" 就是新的 "高价值中心"。
循环收敛
重复 "步骤 2（分配样本）→步骤 3（更新中心）"，直到簇中心的位置变化很小（比如变化量小于 0.001），或者达到预设的迭代次数（比如迭代 100 次），就认为算法收敛，聚类完成。

K-Means 的目标函数（数学本质）

K-Means 的核心是最小化 "簇内平方和（Inertia）"------ 所有样本到其所属簇中心的 "距离平方和"，公式如下：

J = ∑ i = 1 k ∑ x j ∈ C i ∥ x j − μ i ∥ 2 J=∑{i=1}^k∑{x_j∈C_i}∥x_j−μ_i∥^2 J=∑i=1k∑xj∈Ci∥xj−μi∥2

C i C_i Ci：第 i 个簇的所有样本；
μ i μ_i μi：第 i 个簇的中心（簇内样本均值）；
∥ x j − μ i ∥ 2 ∥x_j−μ_i∥^2 ∥xj−μi∥2：样本 x j x_j xj 到簇中心 μ i μ_i μi 的欧氏距离的平方。

这个目标函数的意义很明确：让每个簇内的样本尽可能 "紧凑"，减少簇内的离散程度 ------ 簇内平方和越小，说明聚类效果越好。

用 K-Means 聚类模拟数据

用 sklearn 生成 "自带簇结构的模拟数据"，一步步实现 K-Means 聚类，直观感受其效果。

导入工具与生成数据
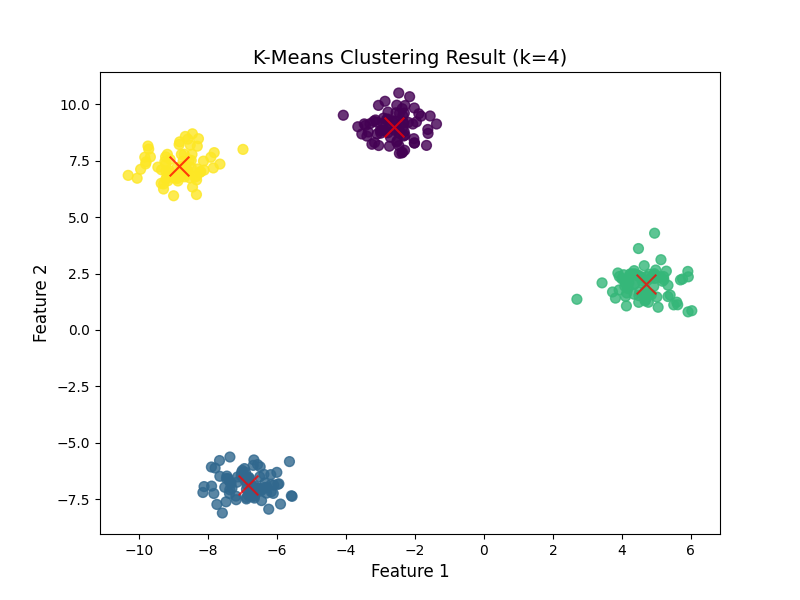
先用 make_blobs 生成 300 个样本，这些样本天然分成 4 个簇（方便验证聚类效果）：

python 复制代码

from sklearn.datasets import make_blobs  # 生成模拟聚类数据
from sklearn.cluster import KMeans      # K-Means算法
import matplotlib.pyplot as plt          # 可视化
import numpy as np                       # 数值计算

# 生成数据：300个样本，4个真实簇，簇内标准差0.6
X, y_true = make_blobs(
    n_samples=300,    # 样本数
    centers=4,        # 真实簇数
    cluster_std=0.6,  # 簇内样本的离散程度（越小越集中）
    random_state=42   # 固定随机种子，结果可复现
)

# 查看数据形状：(样本数, 特征数)，这里是2个特征（方便画图）
print("数据形状：", X.shape)  # 输出：(300, 2)
print("前5个样本：")
print(X[:5])

训练 K-Means 模型
指定簇数 k=4（和真实簇数一致，实际中需通过方法选择 k），训练模型：

python 复制代码

# 初始化K-Means模型，指定簇数k=4
kmeans = KMeans(n_clusters=4, random_state=42)

# 训练模型（无监督学习，不需要y！直接用X训练）
kmeans.fit(X)

# 获取聚类结果
y_pred = kmeans.labels_          # 每个样本的预测簇标签（0/1/2/3）
cluster_centers = kmeans.cluster_centers_  # 最终的4个簇中心（坐标）

print("前10个样本的预测簇标签：", y_pred[:10])
print("4个簇中心的坐标：")
print(cluster_centers)

可视化聚类结果
把样本按预测簇标签上色，再标出簇中心，直观查看聚类效果：

python 复制代码

# 设置画布大小
plt.figure(figsize=(8, 6))

# 画样本点：不同簇用不同颜色
plt.scatter(
    X[:, 0], X[:, 1],  # 样本的两个特征（x轴和y轴）
    c=y_pred,          # 按预测簇标签上色
    s=50,              # 点的大小
    cmap='viridis',    # 配色方案（好看且区分度高）
    alpha=0.8          # 透明度（避免点重叠看不清）
)

# 画簇中心：用红色"X"标记，尺寸大一些
plt.scatter(
    cluster_centers[:, 0], cluster_centers[:, 1],
    c='red',      # 红色
    s=200,        # 比样本点大4倍
    alpha=0.75,   # 略透明
    marker='x'    # 形状为"X"
)

# 添加标题和坐标轴标签
plt.title("K-Means Clustering Result (k=4)", fontsize=14)
plt.xlabel("Feature 1", fontsize=12)
plt.ylabel("Feature 2", fontsize=12)

# 显示图像
plt.show()

可视化结果解读
运行代码后，你会看到：

300 个样本被分成 4 个颜色不同的 "簇"，每个簇内部样本很集中；
4 个红色 "X" 是最终的簇中心，正好位于每个簇的 "中心位置"；
因为我们用 make_blobs 生成的是 "球形簇"，K-Means 几乎完美还原了真实的簇结构（这是 K-Means 对球形簇效果好的特点）。

mathematica 复制代码

数据形状： (300, 2)
前5个样本：
[[ -9.1139443    6.81361629]
 [ -9.35457578   7.09278959]
 [ -2.01567068   8.28177994]
 [ -7.01023591  -6.22084348]
 [-10.06120248   6.71867113]]
前10个样本的预测簇标签： [3 3 0 1 3 1 2 1 0 2]
4个簇中心的坐标：
[[-2.60516878  8.99280115]
 [-6.85126211 -6.85031833]
 [ 4.68687447  2.01434593]
 [-8.83456141  7.24430734]]

如何确定最优簇数 k？（肘部法）

K-Means 需要手动指定簇数 k，但实际中我们不知道 "数据该分多少组"------ 比如用户分 3 组还是 5 组？这时候就需要用 "肘部法（Elbow Method）" 来选择最优 k。

肘部法核心逻辑

簇内平方和（Inertia）是 K-Means 模型的 "损失值"------k 越小，簇内样本越分散，Inertia 越大；k 越大，簇内样本越集中，Inertia 越小。

但当 k 超过 "数据真实簇数" 后，Inertia 的下降速度会突然变慢，形成一个 "肘部"（类似人的胳膊肘），这个 "肘部" 对应的 k 就是最优簇数。

实战：用肘部法选择 k

python 复制代码

# 测试k从1到9的情况，计算每个k的Inertia
inertias = []  # 存储不同k的簇内平方和
k_range = range(1, 10)  # k的取值范围

for k in k_range:
    # 初始化并训练K-Means
    km = KMeans(n_clusters=k, random_state=42)
    km.fit(X)
    # 记录当前k的Inertia
    inertias.append(km.inertia_)

# 画图：k vs Inertia
plt.figure(figsize=(8, 6))
plt.plot(k_range, inertias, marker='o', linestyle='-', color='blue')

# 标记"肘部"位置（这里k=4时是肘部）
plt.scatter(4, inertias[3], color='red', s=150, zorder=5)  # inertias[3]是k=4时的损失值
plt.annotate('Elbow (k=4)', xy=(4, inertias[3]), xytext=(5, inertias[3]+50),
             arrowprops=dict(facecolor='black', shrink=0.05), fontsize=12)

# 添加标签和标题
plt.xlabel('Number of Clusters (k)', fontsize=12)
plt.ylabel('Inertia (Within-Cluster Sum of Squares)', fontsize=12)
plt.title('Elbow Method to Choose Optimal k', fontsize=14)
plt.grid(alpha=0.3)  # 加网格线，方便看坐标
plt.show()

结果解读

运行后会看到：

当 k 从 1→4 时，Inertia 快速下降（簇内样本从 "全挤在 1 个簇" 逐渐变得 "紧凑"）；
当 k 从 4→9 时，Inertia 下降速度明显变慢（再增加 k，簇内紧凑度提升很小，反而可能导致 "过聚类"------ 把本应在一组的样本拆成多组）；
红色标记的 "k=4" 就是 "肘部"，对应数据的真实簇数，是最优选择。

mathematica 复制代码

数据形状： (300, 2)
前5个样本：
[[ -9.1139443    6.81361629]
 [ -9.35457578   7.09278959]
 [ -2.01567068   8.28177994]
 [ -7.01023591  -6.22084348]
 [-10.06120248   6.71867113]]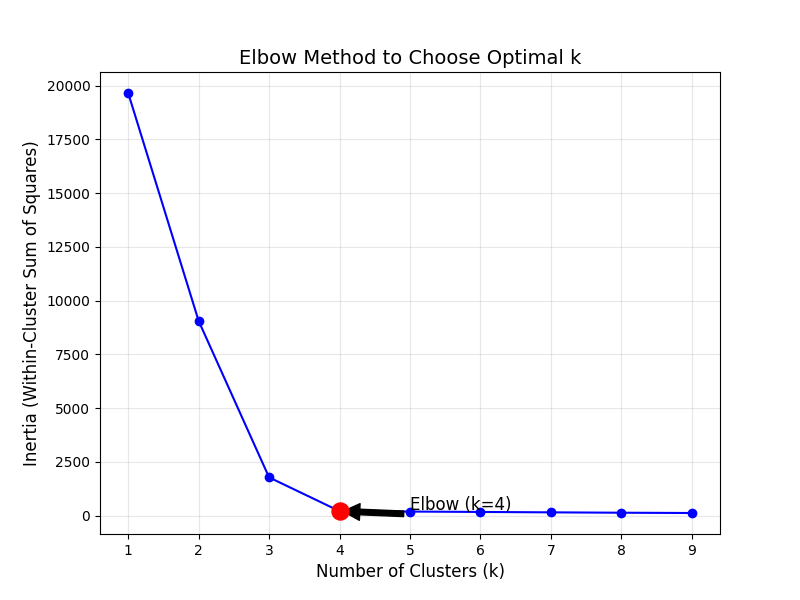

K-Means 的核心特点

优点：

简单直观：原理容易理解，代码实现简单（sklearn 封装完善）；
速度快：时间复杂度低（O (n)，n 是样本数），适合大规模数据（比如 10 万 + 样本）；
效果稳定：只要初始中心不是极端值，最终收敛结果差异不大；
可解释性强：簇中心可以对应业务含义（如 "高价值簇中心" 的 "消费金额 = 5000 元"，可直接解读为该组用户平均消费 5000 元）。

缺点：

需手动指定 k：必须提前确定簇数，没有 "自动选 k" 的完美方法（肘部法是经验方法，不是绝对标准）；
对初始中心敏感 ：极端情况下，随机选的初始中心可能导致 "局部最优"（比如把两个近簇合并）------sklearn 中 KMeans 默认用 n_init=10（重复 10 次选初始中心，取 Inertia 最小的结果），缓解了这个问题；
只适合球形簇：对非球形簇（如 "月牙形、环形"）效果差（因为欧氏距离无法正确衡量 "环形内外" 的相似度）；
对异常值敏感：异常值（离群点）会严重拉偏簇中心（比如一个消费 100 万的异常用户，会让 "高价值簇中心" 大幅偏高）；
对特征尺度敏感 ：如果特征量纲不同（如 "年龄 = 20-60 岁""收入 = 1 万 - 100 万"），收入的数值差异会主导距离计算，导致聚类结果偏向收入 ------ 解决方法是先标准化（StandardScaler）。

K-Means 以其简单、高效的特点，成为处理 "球形簇、大规模数据" 聚类任务的首选。但要注意它的局限性 ------ 非球形簇需用 DBSCAN 等算法，异常值多需先处理，特征尺度不同需先标准化。

层次聚类（Hierarchical Clustering）

层次聚类的核心定义

层次聚类（Hierarchical Clustering）是一种 "递进式" 的聚类方法，它不直接给出最终的簇划分，而是通过逐步合并或分裂样本，构建一个 "树状结构（树状图 / Dendrogram）"，最终通过 "切割树状图" 得到任意数量的簇。

可以类比成 "整理文件夹"：

一开始每个文件都是独立文件夹（每个样本是一个簇）；
逐步把内容相似的文件夹合并（相似样本合并成大簇）；
最后形成一个 "根文件夹包含所有文件" 的树形结构（所有样本属于一个大簇）；
想分 3 组就在 "树的第三层" 切割，想分 5 组就在 "第五层" 切割 ------ 完全灵活，无需提前定簇数。

层次聚类的两种核心策略

根据 "合并还是分裂" 的逻辑，层次聚类分为两类，实际中 90% 以上用第一种：

策略类型	英文名	核心逻辑	特点
凝聚式层次聚类	Agglomerative Clustering	自底向上：从 "每个样本是一个簇" 开始，逐步合并最相似的簇	最常用，适合大多数场景，计算量相对小
分裂式层次聚类	Divisive Clustering	自顶向下：从 "所有样本是一个簇" 开始，逐步分裂成小簇	极少用，计算量大（每次分裂都要评估所有样本），只适合小数据

重点学习凝聚式层次聚类 （sklearn 中对应的类是 AgglomerativeClustering），这是工业界的主流选择。

凝聚式层次聚类的核心步骤

凝聚式层次聚类的逻辑非常清晰，只有 3 步，循环执行直到所有样本合并成一个簇：

初始化：将每个样本视为一个独立的簇（假设有 n 个样本，初始就有 n 个簇）；
找最相似的簇：计算所有簇之间的 "相似度"（或 "距离"），找到最相似的一对簇；
合并簇：将这对最相似的簇合并成一个新簇；
循环：重复步骤 2-3，直到所有簇合并成一个簇（或达到预设的簇数）。

关键问题：如何计算 "簇与簇之间的距离"？（这是层次聚类的核心，称为 "Linkage 方法"）

关键参数：簇间距离的计算方式（Linkage 方法）

当两个簇包含多个样本时，不能像 "样本间距离" 那样直接算两点距离，需要定义 "簇间距离"。sklearn 中 AgglomerativeClustering 支持 4 种常用 Linkage 方法，效果和适用场景差异很大：

Linkage 方法	核心逻辑（簇 A 和簇 B 的距离）	特点	适用场景
ward	合并后 "簇内方差增加最小" 的距离（默认）	最稳定，能生成紧凑、均衡的簇，类似 K-Means	大多数场景的首选，尤其是簇大小相近时
average	簇 A 所有样本与簇 B 所有样本的 "平均距离"	折中选择，对异常值比 ward 略鲁棒	簇大小差异较大，或有少量异常值时
complete	簇 A 所有样本与簇 B 所有样本的 "最大距离"（最远点距离）	能避免簇被 "拉长"，但对异常值敏感	希望簇结构紧凑，不允许 "长尾样本" 时
single	簇 A 所有样本与簇 B 所有样本的 "最小距离"（最近点距离）	容易形成 "链式簇"（一串样本连在一起）	适合样本呈 "链状分布"（如地理上的道路样本）

举个直观例子：簇 A 有样本 [1,3]，簇 B 有样本 [5,7]

single 距离： m i n ( ∣ 1 − 5 ∣ , ∣ 1 − 7 ∣ , ∣ 3 − 5 ∣ , ∣ 3 − 7 ∣ ) = 2 min (|1-5|, |1-7|, |3-5|, |3-7|) = 2 min(∣1−5∣,∣1−7∣,∣3−5∣,∣3−7∣)=2（1 和 5 的距离）；
complete 距离： m a x ( . . . ) = 6 max (...) = 6 max(...)=6（1 和 7 的距离）；
average 距离： ( 4 + 6 + 2 + 4 ) / 4 = 4 (4+6+2+4)/4 = 4 (4+6+2+4)/4=4；
ward 距离：合并前 A 的方差 = 1，B 的方差 = 1，总方差 = 2；合并后簇 [1,3,5,7] 的方差 = 6，方差增加 = 6-2=4 → ward 距离 = 4。

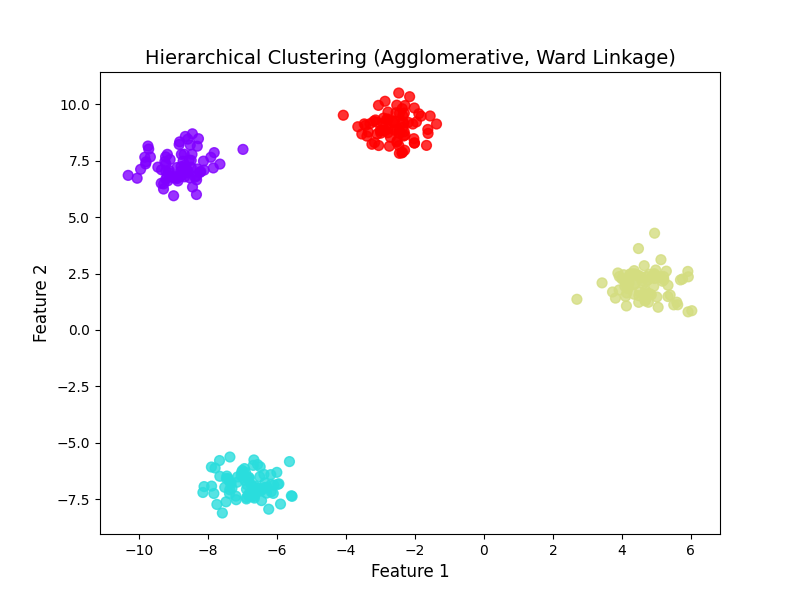
用 AgglomerativeClustering 实现层次聚类

用和 K-Means 相同的模拟数据（300 个样本，4 个球形簇），对比两种算法的聚类效果：

python 复制代码

from sklearn.datasets import make_blobs
from sklearn.cluster import AgglomerativeClustering
import matplotlib.pyplot as plt

# 1. 生成和K-Means相同的模拟数据（保证对比公平）
X, y_true = make_blobs(
    n_samples=300,
    centers=4,
    cluster_std=0.6,
    random_state=42
)

# 2. 初始化凝聚式层次聚类模型
# 关键参数：n_clusters=4（最终想分4个簇），linkage='ward'（用ward方法计算簇间距离）
hc = AgglomerativeClustering(
    n_clusters=4,
    linkage='ward'  # 首选ward方法，效果接近K-Means
)

# 3. 训练模型并获取聚类结果（fit_predict直接返回簇标签）
y_pred_hc = hc.fit_predict(X)

# 4. 可视化聚类结果（和K-Means对比）
plt.figure(figsize=(8, 6))
# 画样本点：按层次聚类标签上色
plt.scatter(
    X[:, 0], X[:, 1],
    c=y_pred_hc,
    s=50,
    cmap='rainbow',  # 用和K-Means不同的配色，方便区分
    alpha=0.8
)
plt.title("Hierarchical Clustering (Agglomerative, Ward Linkage)", fontsize=14)
plt.xlabel("Feature 1", fontsize=12)
plt.ylabel("Feature 2", fontsize=12)
plt.show()

结果解读

运行后会发现：

层次聚类（ward linkage）的结果和 K-Means 几乎一致，4 个簇的划分完全对应数据的真实结构；
这是因为数据是 "球形簇"，ward 方法（最小化簇内方差）的目标和 K-Means 的目标（最小化簇内平方和）本质一致，所以效果相近。

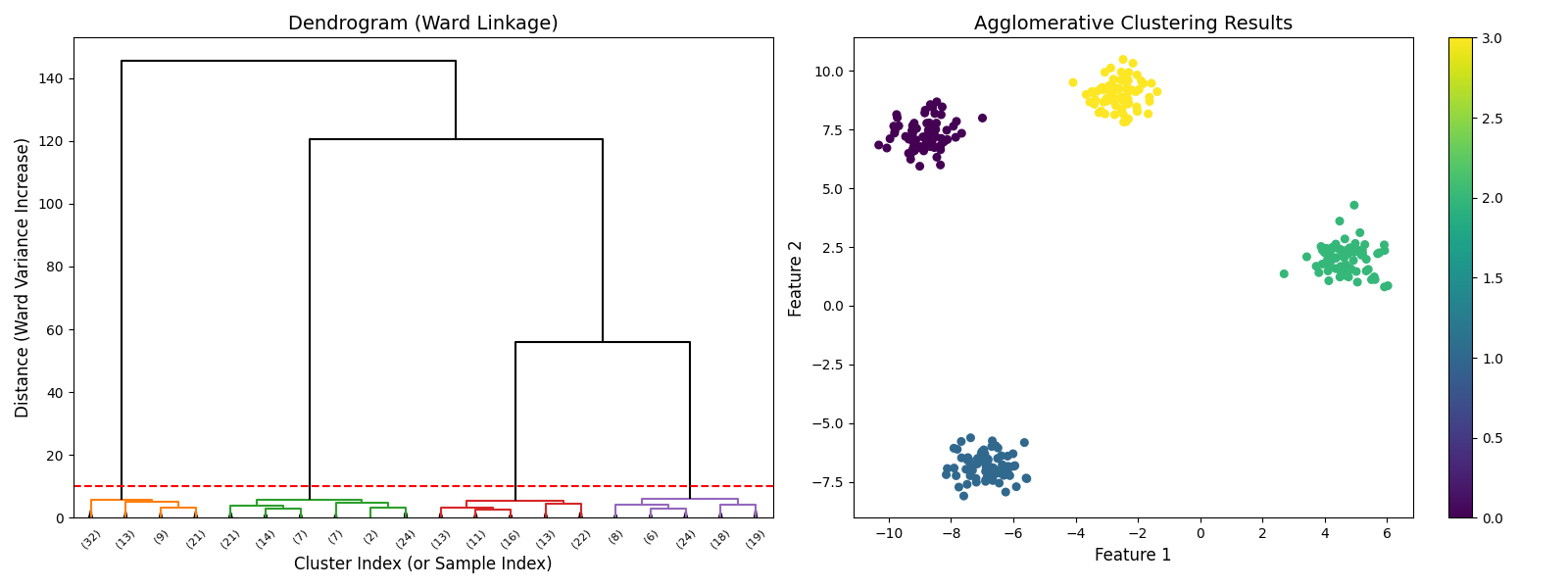
用树状图（Dendrogram）可视化聚类过程

层次聚类的最大优势是 "可通过树状图展示聚类递进关系"，但 sklearn 的 AgglomerativeClustering 不直接支持画树状图，需要用 scipy 的 hierarchy 模块实现：

python 复制代码

from sklearn.datasets import make_blobs
from sklearn.cluster import AgglomerativeClustering
from scipy.cluster.hierarchy import dendrogram, linkage
import matplotlib.pyplot as plt

# 1. 生成和K-Means相同的模拟数据（保证对比公平）
X, y_true = make_blobs(
    n_samples=300,
    centers=4,
    cluster_std=0.6,
    random_state=42
)

# 2. 初始化凝聚式层次聚类模型
# 关键参数：n_clusters=4（最终想分4个簇），linkage='ward'（用ward方法计算簇间距离）
hc = AgglomerativeClustering(
    n_clusters=4,
    linkage='ward'  # 首选ward方法，效果接近K-Means
)

# 3. 执行聚类并获取预测结果
y_pred = hc.fit_predict(X)

# 4. 用scipy的linkage函数计算"簇间距离矩阵"（对应层次聚类的合并过程）
# method='ward'：和sklearn中一致的距离计算方法
Z = linkage(X, method='ward')

# 5. 创建两个子图：左侧显示树状图，右侧显示聚类结果
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 6))

# 左侧：绘制树状图
dendrogram(
    Z,
    truncate_mode='lastp',  # 只显示最后p个合并步骤（避免树状图过长）
    p=20,                   # 显示最后20个合并步骤
    leaf_rotation=45,       # 样本标签旋转45度，避免重叠
    leaf_font_size=8,       # 样本标签字体大小
    show_contracted=True,   # 显示被压缩的簇（用...表示）
    color_threshold=10,     # 距离超过10的合并步骤用黑色（方便识别簇划分）
    above_threshold_color='black',
    ax=ax1
)
ax1.set_title("Dendrogram (Ward Linkage)", fontsize=14)
ax1.set_xlabel("Cluster Index (or Sample Index)", fontsize=12)
ax1.set_ylabel("Distance (Ward Variance Increase)", fontsize=12)
ax1.axhline(y=10, color='r', linestyle='--')  # 画一条水平参考线（y=10）

# 右侧：显示聚类结果
scatter = ax2.scatter(X[:, 0], X[:, 1], c=y_pred, cmap='viridis', s=30)
ax2.set_title("Agglomerative Clustering Results", fontsize=14)
ax2.set_xlabel("Feature 1", fontsize=12)
ax2.set_ylabel("Feature 2", fontsize=12)
plt.colorbar(scatter, ax=ax2)

plt.tight_layout()
plt.show()

树状图解读

树状图的横轴是 "样本或簇的索引"，纵轴是 "合并时的簇间距离"（ward 方法中是 "方差增加量"）：

合并过程：最底部的每一个 "小横线" 代表 "两个样本合并成一个小簇"；往上的 "横线" 代表 "两个小簇合并成一个大簇"；最顶部的横线代表 "所有簇合并成一个大簇"；
簇数选择：用 "水平直线切割树状图"，切割线与多少条竖线相交，就得到多少个簇。比如图中红色虚线（y=10）切割后，与 4 条竖线相交 → 得到 4 个簇，正好是数据的真实簇数；
簇的相似度：纵轴距离越小，说明合并的两个簇越相似（比如底部合并样本的距离接近 0，说明这些样本几乎一样）；距离越大，说明合并的簇差异越大（顶部合并大簇的距离超过 20，说明这两个大簇差异很大）。

层次聚类 vs K-Means：核心差异对比

对比维度	K-Means	层次聚类（凝聚式，ward linkage）
是否需指定簇数 k	必须提前指定（如 k=4）	无需提前指定（切割树状图灵活选 k）
对初始值敏感程度	中等（默认 n_init=10 缓解）	不敏感（合并过程唯一，无初始值）
时间复杂度	低（O (n)，适合 10 万 + 样本）	高（O (n²)，适合 1 万样本以内）
可视化能力	弱（只能看最终簇分布）	强（树状图展示完整合并过程）
对簇形状的适应性	只适合球形簇	适合球形簇（ward）、紧凑非球形簇（complete）
对异常值的敏感性	高（异常值拉偏簇中心）	中等（ward 方法对异常值比 K-Means 略鲁棒）
适用场景	大规模、球形簇数据	中小规模、需灵活选 k、需展示聚类过程的数据

举个实际业务例子：

电商 "100 万用户分群" → 用 K-Means（速度快）；
科研 "1000 个基因样本分类" → 用层次聚类（需通过树状图分析基因间的亲缘关系，灵活选 k）。

层次聚类的核心特点

优点：

无需手动选 k：通过树状图灵活切割，可得到任意数量的簇，解决了 K-Means 的核心痛点；
结果稳定：无初始值影响，只要距离方法固定，聚类结果唯一；
可解释性极强：树状图能直观展示 "样本→小簇→大簇" 的递进关系，适合业务分析（如 "用户分群树状图" 可看出 "高活跃用户" 是从 "年轻高活跃" 和 "中年高活跃" 合并来的）；
对簇形状适应性略强：complete linkage 方法能处理部分非球形的紧凑簇（比 K-Means 好）。

缺点：

速度慢：时间复杂度 O (n²)，样本数超过 1 万时会明显卡顿，无法处理大规模数据；
内存消耗大：需存储 n×n 的距离矩阵，样本多时有内存溢出风险；
容易形成 "链式簇"：single linkage 方法会导致 "相似样本串成一条链"，形成不合理的长簇；
无法撤销合并：合并过程是 "不可逆" 的（一旦两个簇合并，后续无法拆分），可能导致 "早期错误合并影响最终结果"（如把两个差异大的小簇误合并，后续无法分开）。

当数据量不大（1 万以内）、需要灵活选择簇数、或需要展示聚类过程时，层次聚类是比 K-Means 更好的选择，尤其是 ward linkage 方法在球形簇数据上的效果可媲美 K-Means，且无需提前定 k。

DBSCAN 与密度聚类

DBSCAN 的核心定义

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）是一种基于密度的聚类算法。它的核心思想不是 "找中心"（如 K-Means）或 "逐步合并"（如层次聚类），而是：

"把数据中'密度高'的区域视为簇，'密度低'的区域视为簇之间的边界，'完全没有密度'的孤立点视为异常值（噪声）。"

可以类比成 "在地图上找城市"：

人口密集的区域（如市中心）是 "簇"（城市）；
人口稀少的郊区是 "簇之间的边界"；
偏远的孤家寡人是 "异常值"（不属于任何城市）。

无论城市是圆形、条形还是不规则形状，只要人口密集，就能被识别出来 ------ 这就是 DBSCAN 处理任意形状簇的核心能力。

DBSCAN 的 3 个关键概念

DBSCAN 通过两个参数定义 "密度"，并基于密度将样本分为三类，这是理解算法的基础：

概念	定义
ε（eps）	邻域半径：以某个样本为中心，半径 ε 范围内的所有样本都视为 "邻居"。
min_samples	核心点阈值：如果一个样本的 ε 邻域内至少包含 min_samples 个样本（包括自身），则该样本是 "核心点"。
核心点（Core Point）	满足 "ε 邻域内样本数 ≥ min_samples" 的样本，是簇的 "核心组成部分"。
边界点（Border Point）	ε 邻域内样本数 < min_samples，但落在某个核心点的 ε 邻域内的样本，属于簇但不是核心。
噪声点（Noise Point）	既不是核心点，也不是边界点的样本，不属于任何簇，视为异常值。

举个例子：设 ε=2，min_samples=5

样本 A 的 ε 邻域内有 6 个样本 → 核心点；
样本 B 的 ε 邻域内有 3 个样本，但在 A 的 ε 邻域内 → 边界点；
样本 C 的 ε 邻域内只有 1 个样本，且不在任何核心点的邻域内 → 噪声点。

DBSCAN 的核心工作流程

基于上述概念，DBSCAN 的聚类过程可拆解为 4 步，逻辑清晰且无迭代：

遍历所有样本：对每个未标记的样本，计算其 ε 邻域内的样本数；
标记核心点：若样本的 ε 邻域内样本数 ≥ min_samples，标记为核心点；
扩展簇：对每个核心点，将其 ε 邻域内的所有样本（包括核心点和边界点）归为同一个簇；再递归扩展 "这些样本中核心点的 ε 邻域"，直到没有新样本可加入簇；
标记噪声：遍历完所有核心点后，未被归入任何簇的样本（既不是核心点也不是边界点）标记为噪声点。

简单说：DBSCAN 的簇是 "所有能通过核心点的 ε 邻域连接起来的样本集合"，噪声是 "孤立的非核心点"。

用 DBSCAN 处理非球形簇（K-Means 的短板场景）

K-Means 和层次聚类（ward）对 "球形簇" 效果好，但对 "月牙形、环形" 等非球形簇完全失效，而 DBSCAN 能轻松处理。我们用make_moons生成月牙形数据演示：

python 复制代码

from sklearn.datasets import make_moons
from sklearn.cluster import DBSCAN
import matplotlib.pyplot as plt
import numpy as np

# 1. 生成月牙形数据（含少量噪声）
X, y_true = make_moons(
    n_samples=300,  # 300个样本
    noise=0.05,     # 少量噪声（模拟真实数据）
    random_state=42
)

# 2. 初始化DBSCAN模型（关键参数：eps和min_samples）
# eps=0.2：邻域半径（需根据数据密度调整）
# min_samples=5：核心点阈值（一般取5-10）
dbscan = DBSCAN(eps=0.2, min_samples=5)

# 3. 训练模型并获取结果（无监督，无需y）
y_pred = dbscan.fit_predict(X)  # 标签为-1的是噪声点

# 4. 统计结果
n_clusters = len(set(y_pred)) - (1 if -1 in y_pred else 0)  # 簇的数量（排除噪声）
n_noise = list(y_pred).count(-1)  # 噪声点数量
print(f"发现的簇数：{n_clusters}")
print(f"噪声点数量：{n_noise}")

# 5. 可视化结果（噪声点用黑色×标记）
plt.figure(figsize=(8, 6))
# 画正常簇的样本（非-1标签）
for cluster in set(y_pred):
    if cluster == -1:
        continue  # 跳过噪声点，单独画
    mask = y_pred == cluster
    plt.scatter(
        X[mask, 0], X[mask, 1],
        s=50,
        label=f"Cluster {cluster}"
    )
# 画噪声点（黑色×，尺寸小一些）
mask_noise = y_pred == -1
plt.scatter(
    X[mask_noise, 0], X[mask_noise, 1],
    s=30,
    c='black',
    marker='x',
    label="Noise"
)

plt.title("DBSCAN Clustering (Moons Dataset)", fontsize=14)
plt.xlabel("Feature 1", fontsize=12)
plt.ylabel("Feature 2", fontsize=12)
plt.legend()
plt.show()

结果解读

运行后会看到：

DBSCAN 完美识别出两个月牙形的簇（标签 0 和 1），没有将它们误合并；
只有极少数样本被标记为噪声点（黑色 ×），符合我们添加的少量噪声设定；
如果用 K-Means 处理这个数据，会把 "月牙的内侧和外侧" 误分为不同簇（因为 K-Means 只能识别球形簇），而 DBSCAN 完全不会 ------ 这就是密度聚类的优势。

mathematica 复制代码

发现的簇数：2
噪声点数量：0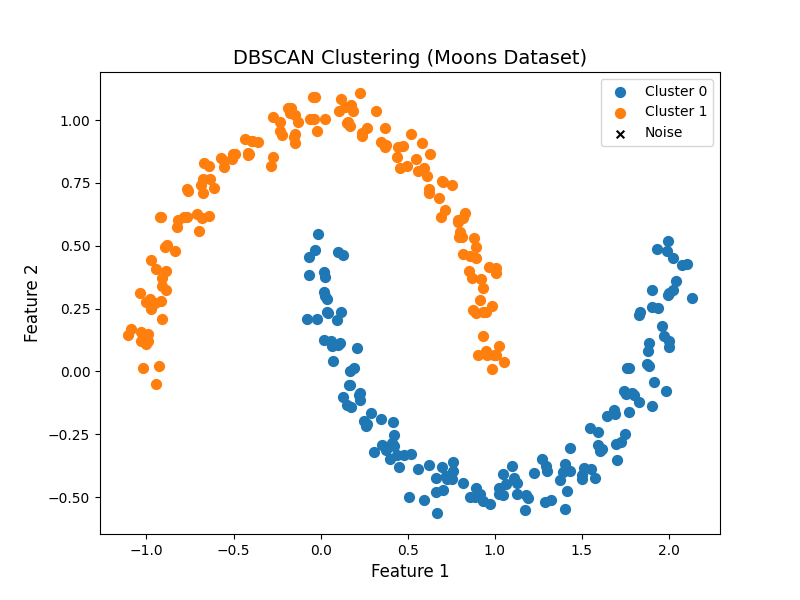

如何确定最优的 ε 和 min_samples？

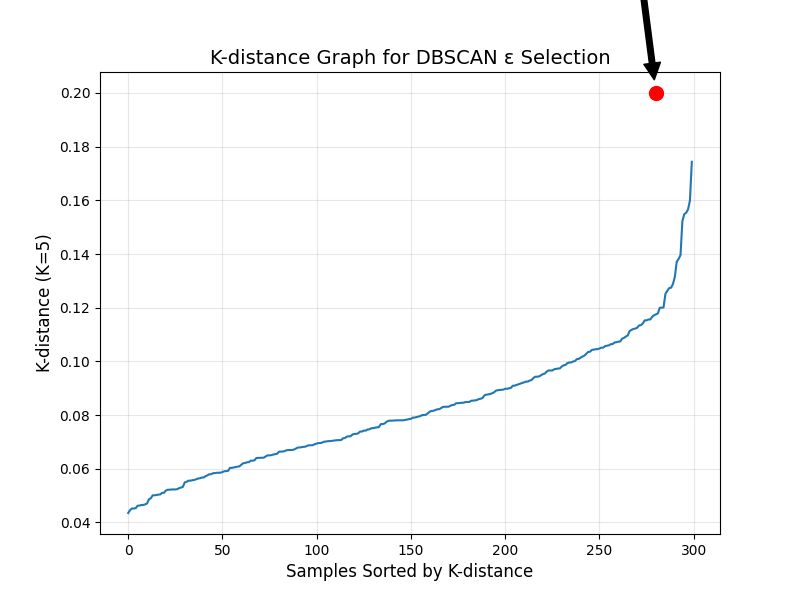
DBSCAN 的效果完全依赖于 ε（邻域半径）和 min_samples（核心点阈值）的选择，参数错了会导致 "所有样本都是噪声" 或 "所有样本归为一个簇"。这里提供最实用的参数调优方法：K - 距离图（K-distance Graph）。

方法原理

K - 距离图的核心逻辑：

对每个样本，计算它到 "第 K 个最近邻样本" 的距离（K=min_samples）；
把所有样本的 "第 K 个最近邻距离" 按从小到大排序，画成折线图；
图中 "突然陡峭的拐点" 对应的距离，就是最优的 ε------ 拐点前的样本 "距离近，密度高"（属于簇），拐点后的样本 "距离远，密度低"（属于噪声）。

用 K - 距离图选 ε

python 复制代码

from sklearn.neighbors import NearestNeighbors
import numpy as np
import matplotlib.pyplot as plt

# 1. 设定min_samples=5（先固定一个合理的K值，通常取5-10）
min_samples = 5

# 2. 计算每个样本到"第5个最近邻"的距离
neighbors = NearestNeighbors(n_neighbors=min_samples)  # 找每个样本的5个最近邻
neighbors_fit = neighbors.fit(X)
distances, _ = neighbors_fit.kneighbors(X)  # distances.shape=(n_samples, min_samples)

# 3. 提取每个样本的"第5个最近邻距离"（索引4，因为从0开始），并排序
k_distances = distances[:, min_samples - 1]  # 第5个最近邻是索引4
k_distances_sorted = np.sort(k_distances)

# 4. 画K-距离图
plt.figure(figsize=(8, 6))
plt.plot(k_distances_sorted)
plt.xlabel("Samples Sorted by K-distance", fontsize=12)
plt.ylabel(f"K-distance (K={min_samples})", fontsize=12)
plt.title("K-distance Graph for DBSCAN ε Selection", fontsize=14)
# 标记拐点（示例中拐点在距离≈0.2处，对应最优ε=0.2）
plt.scatter(x=280, y=0.2, color='red', s=100, zorder=5)
plt.annotate('Elbow (ε≈0.2)', xy=(280, 0.2), xytext=(200, 0.3),
             arrowprops=dict(facecolor='black', shrink=0.05), fontsize=12)
plt.grid(alpha=0.3)
plt.show()

结果解读

图中折线在 "样本排序 280 左右" 出现明显拐点：

拐点前（前 280 个样本）：K - 距离缓慢增长（样本密度高，最近邻距离近）；
拐点后（280 个样本后）：K - 距离快速增长（样本密度低，最近邻距离远）；
拐点对应的距离≈0.2，就是最优的 ε 值 ------ 和我们之前实战中用的 ε=0.2 完全一致，验证了方法的有效性。

DBSCAN vs K-Means vs 层次聚类：

对比维度	K-Means	层次聚类（凝聚式）	DBSCAN
簇形状适应性	仅球形簇	球形 / 紧凑非球形	任意形状（如月牙、环形）
是否需指定簇数 k	必须指定	灵活切割树状图	自动确定簇数
是否识别异常值	不能（异常值拉偏中心）	不能（异常值合并入簇）	自动标记噪声点
时间复杂度	低（O (n)，适合大数据）	高（O (n²)，适合小数据）	中（O (n log n)，看实现）
对参数敏感性	低（n_init=10 缓解）	中（linkage 影响大）	高（ε 和 min_samples 关键）
对密度差异的适应性	低（密度不均时效果差）	低（密度不均时合并错误）	低（密度差异大时失效）
适用场景	大规模、球形簇、密度均匀	中小规模、需展示聚类过程	任意形状簇、需异常检测

DBSCAN 的核心特点

优点：

无需指定簇数：自动根据密度确定簇的数量，解决了 K-Means 和层次聚类的选 k 难题；
能识别任意形状簇：对月牙形、环形等非球形簇效果远超 K-Means；
自动识别异常值：天然支持异常检测（噪声点），无需额外算法；
对噪声不敏感：异常值不会影响簇的形成（K-Means 中异常值会拉偏簇中心）。

缺点：

参数极度敏感：ε 和 min_samples 的微小变化会导致结果天差地别，调参难度高；
不适合密度差异大的数据：如果簇 A 密度很高、簇 B 密度很低，DBSCAN 会把簇 B 误判为噪声；
对高维数据效果差：高维数据中 "距离" 的定义会失效（维度灾难），导致密度计算不准；
大规模数据速度慢：传统 DBSCAN 需计算所有样本的邻域，数据量大时耗时严重（可改用优化版如 HDBSCAN）。

当数据的簇不是球形、且需要识别异常值时，DBSCAN 是无可替代的选择。但要注意它的短板 ------ 参数难调、不适合密度不均的数据，实际使用中需结合 K - 距离图仔细调参。

降维算法

PCA（主成分分析）

什么是 PCA？

PCA（Principal Component Analysis，主成分分析）是一种线性降维算法，它通过将原始的高维特征空间，转换为一个新的低维 "主成分空间"，实现两个核心目标：

最大程度保留数据信息：新的主成分能 "解释" 原始数据中大部分的 "变异（方差）"------ 方差越大，说明该维度包含的信息越多；
去除特征冗余：新的主成分之间是 "正交的（互不相关）"，避免了原始特征间的多重共线性（如 "身高（厘米）" 和 "身高（米）" 高度相关，PCA 能将其压缩为 1 个主成分）。

可以类比成 "拍 3D 物体的 2D 照片"：

3D 物体（如正方体）是高维数据（3 个维度）；
拍照片时选择 "正面角度"（对应主成分 1），能最大程度展示物体的形状（保留最多信息）；
照片是 2D 的（降维后），但仍能清晰识别物体 ------ 这就是 PCA 的核心逻辑：用低维保留高维的核心信息。

PCA 的核心思想：找 "方差最大的方向"

PCA 的数学逻辑可以简化为 3 步，核心是找到 "能解释最多方差的投影方向"（即主成分）：

数据中心化：对每个特征，减去该特征的均值（让特征均值为 0）------ 这是 PCA 的前提，避免 "数值大的特征主导方差计算"（如 "收入 = 10 万" 的方差远大于 "年龄 = 30"，不中心化会让 PCA 只关注收入）。
找主成分方向 ：
- 主成分 1（第一主成分）：是原始特征空间中 "方差最大的方向"------ 数据在这个方向上的分布最分散，包含的信息最多；
- 主成分 2（第二主成分）：是 "与主成分 1 正交（垂直）" 且 "方差第二大的方向"------ 在不重复主成分 1 信息的前提下，保留次多信息；
- 以此类推，主成分的数量最多等于原始特征的数量（但我们通常只选前 k 个主成分，实现降维）。
数据投影：将原始数据 "投影" 到前 k 个主成分构成的低维空间中，得到降维后的特征。

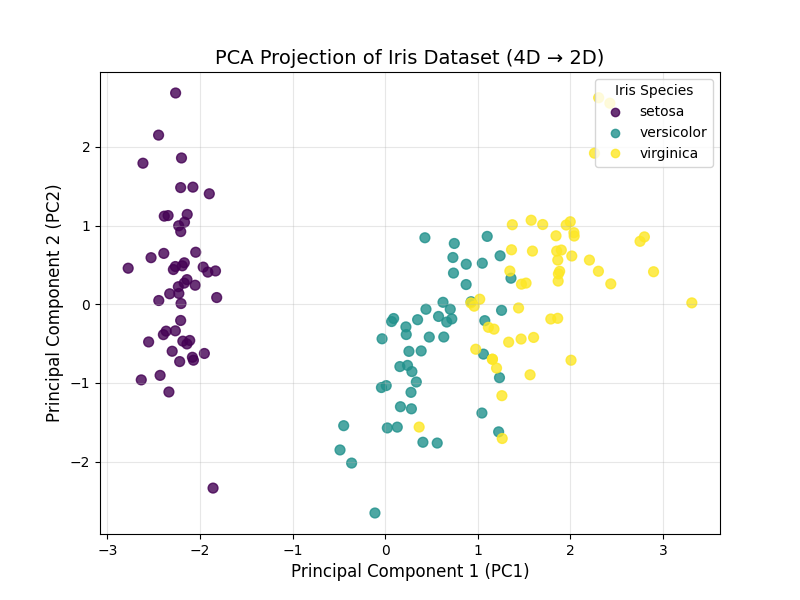
用 PCA 降维并可视化鸢尾花数据

鸢尾花数据集有 4 个特征（花萼长、花萼宽、花瓣长、花瓣宽），用 PCA 将其降维到 2 个维度，方便画图展示：

python 复制代码

from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler  # PCA前建议标准化（除中心化外，还统一量纲）
import matplotlib.pyplot as plt

# 1. 加载数据并预处理
iris = load_iris()
X = iris.data  # 原始4个特征
y = iris.target  # 真实类别（仅用于可视化上色，无监督学习不依赖y）

# PCA对特征尺度敏感，先标准化（均值0，方差1）------关键步骤！
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 2. 初始化PCA模型，降维到2个主成分
pca = PCA(n_components=2)  # n_components：降维后的维度数

# 3. 拟合PCA并降维（无监督，仅用X_scaled）
X_pca = pca.fit_transform(X_scaled)

# 查看降维前后的形状
print(f"原始数据形状：{X.shape}（4个特征）")
print(f"降维后数据形状：{X_pca.shape}（2个主成分）")

输出结果：

mathematica 复制代码

原始数据形状：(150, 4)（4个特征）
降维后数据形状：(150, 2)（2个主成分）

150 个样本的 4 个特征，成功压缩到 2 个主成分，维度减少 50%。

可视化降维结果

python 复制代码

plt.figure(figsize=(8, 6))
# 按真实类别上色（方便观察簇结构）
scatter = plt.scatter(
    X_pca[:, 0], X_pca[:, 1],  # 第一主成分（x轴）、第二主成分（y轴）
    c=y,  # 按真实类别y上色
    cmap='viridis',  # 配色方案
    s=50,
    alpha=0.8
)

# 添加图例（对应鸢尾花的3个品种）
plt.legend(
    scatter.legend_elements()[0],  # 图例标记
    iris.target_names,  # 图例名称（setosa, versicolor, virginica）
    loc="upper right",
    title="Iris Species"
)

# 添加标题和标签
plt.title("PCA Projection of Iris Dataset (4D → 2D)", fontsize=14)
plt.xlabel("Principal Component 1 (PC1)", fontsize=12)
plt.ylabel("Principal Component 2 (PC2)", fontsize=12)
plt.grid(alpha=0.3)
plt.show()

结果解读：

降维后的 2 个主成分，依然能清晰区分鸢尾花的 3 个品种：setosa（紫色）完全分离，versicolor（黄色）和 virginica（绿色）有少量重叠；
这说明 PCA 在 "压缩维度" 的同时，保留了原始数据的核心分类信息 ------ 如果直接用 4 个特征画图，我们无法直观看到这种簇结构，而 PCA 通过降维实现了 "高维数据可视化"。

关键指标：方差贡献率（Explained Variance Ratio）

PCA 的核心优势是 "可量化保留的信息比例"，通过explained_variance_ratio_查看每个主成分解释的原始数据方差占比：

python 复制代码

# 查看每个主成分的方差贡献率
print("各主成分的方差贡献率：", pca.explained_variance_ratio_)
# 查看累计方差贡献率（前k个主成分共保留多少信息）
print("累计方差贡献率（前2个主成分）：", sum(pca.explained_variance_ratio_))

输出结果：

plaintext 复制代码

各主成分的方差贡献率： [0.72962445 0.22850762]
累计方差贡献率（前2个主成分）： 0.9581320731874407

第一主成分（PC1）解释了原始数据 72.96% 的方差（包含 72.96% 的信息）；
第二主成分（PC2）解释了 22.85% 的方差；
前 2 个主成分共解释了 95.81% 的方差 ------ 意味着我们用 2 个维度，保留了原始 4 个维度 95.81% 的信息，仅丢失 4.19% 的信息，降维效果极佳！

如何确定 "降维到多少维（k）"？

实际中我们不会随意选 k，而是通过 "累计方差贡献率曲线" 确定：通常选择 "累计贡献率≥95%" 的最小 k（保证保留绝大多数信息），或 "累计贡献率≥80%"（允许少量信息丢失，追求更高降维率）。

python 复制代码

# 先拟合一个"全维度PCA"（不指定n_components，保留所有主成分）
pca_full = PCA().fit(X_scaled)

# 计算累计方差贡献率
cumulative_var_ratio = pca_full.explained_variance_ratio_.cumsum()

# 画图：主成分数量 vs 累计方差贡献率
plt.figure(figsize=(8, 6))
plt.plot(
    range(1, len(cumulative_var_ratio) + 1),  # x轴：主成分数量（1-4）
    cumulative_var_ratio,                     # y轴：累计方差贡献率
    marker='o',
    linestyle='-',
    color='blue'
)

# 画参考线：累计贡献率95%和80%
plt.axhline(y=0.95, color='red', linestyle='--', label='95% Variance')
plt.axhline(y=0.8, color='green', linestyle='--', label='80% Variance')

# 标记达到95%和80%所需的主成分数量
k_95 = next(i for i, val in enumerate(cumulative_var_ratio) if val >= 0.95) + 1
k_80 = next(i for i, val in enumerate(cumulative_var_ratio) if val >= 0.8) + 1
plt.scatter(k_95, 0.95, color='red', s=100, zorder=5)
plt.scatter(k_80, 0.8, color='green', s=100, zorder=5)

# 添加标签和图例
plt.xlabel("Number of Principal Components", fontsize=12)
plt.ylabel("Cumulative Explained Variance Ratio", fontsize=12)
plt.title("Cumulative Variance vs. Number of Components (Iris Dataset)", fontsize=14)
plt.legend()
plt.grid(alpha=0.3)
plt.show()

print(f"达到95%累计方差需{k_95}个主成分")
print(f"达到80%累计方差需{k_80}个主成分")

结果解读：

达到 80% 累计方差需 2 个主成分（PC1 解释 72.96%，PC1+PC2 远超 80%）；
达到 95% 累计方差需 2 个主成分 ------ 这就是我们之前选择 n_components=2 的原因，既降维又保信息。

PCA 的经典应用场景

PCA 不仅用于可视化，还有三大核心应用：

高维数据压缩 ：
- 例：100 个用户行为特征 → 用 PCA 压缩到 10 个主成分，保留 95% 信息；
- 价值：减少模型计算量（如 KNN、SVM 在高维数据上速度慢，压缩后提速 10 倍），降低内存消耗。
去噪（Noise Reduction） ：
- 原理：噪声通常对应 "低方差主成分"（信号对应高方差主成分）；
- 例：手写数字图片（8x8=64 像素，含噪声）→ 用 PCA 保留前 20 个主成分（高方差，信号），丢弃后 44 个主成分（低方差，噪声）→ 重构图片，噪声明显减少。
特征预处理（避免多重共线性） ：
- 例：线性回归中，"身高（厘米）" 和 "身高（米）" 高度相关（多重共线性），导致模型系数不稳定；
- 用 PCA 将其压缩为 1 个主成分，消除共线性，模型更稳定。

PCA 的核心特点

优点：

高效降维：计算速度快，适合大规模高维数据（如 10 万样本、1000 特征）；
可解释性强：通过方差贡献率量化保留的信息比例，便于业务决策（如 "用 2 个主成分保留 95% 信息，可行"）；
去噪与消除共线性：一举解决高维数据的两大痛点；
通用性强：不依赖数据分布，几乎适用于所有类型的数值型数据（图像、文本向量、传感器数据等）。

缺点：

仅支持线性降维：无法处理特征间的非线性关系（如 "年龄对收入的影响先增后减"），对非线性数据降维时会丢失大量信息（需用 t-SNE 等非线性降维算法）；
主成分难以解读：主成分是原始特征的 "线性组合"（如 PC1=0.5× 花萼长 + 0.3× 花瓣长 - 0.2× 花萼宽），无法直接对应业务含义（如 "PC1 代表什么？" 难以回答）；
对特征尺度敏感：必须先标准化（或归一化），否则数值大的特征会主导主成分（如 "收入 = 10 万" 会让 PCA 忽略 "年龄 = 30"）；
可能丢失关键低频信息：如果重要信息集中在低方差主成分（如异常值信号），PCA 会误将其当作噪声丢弃。

PCA 以其高效、可量化、通用性强的特点，成为处理高维数据的 "首选第一步"------ 几乎所有涉及高维数据的项目（如图像识别、用户行为分析），都会先用 PCA 做探索性分析或预处理。但要注意它的线性局限性，非线性数据需搭配 t-SNE 等算法。

LDA（有监督）与 t-SNE（非线性）

LDA（Linear Discriminant Analysis）------ 为分类而生的有监督降维

LDA 和 PCA 同属线性降维，但核心目标完全不同：PCA 是 "无监督"，只关注保留数据方差；LDA 是 "有监督"，会利用类别标签信息，目标是 "让降维后的数据更易分类"。

LDA 的核心思想：最大化 "类间差异"，最小化 "类内差异"

LDA 的核心逻辑围绕 "分类效果" 设计，假设数据有类别标签，它会寻找这样的投影方向：

类间距离最大化：不同类别的样本在投影后尽可能远离（比如 "猫" 和 "狗" 的投影中心相距越远越好）；
类内距离最小化：同一类别的样本在投影后尽可能集中（比如所有 "猫" 的投影点紧凑分布）。

可以类比成 "调整相机角度拍动物"：PCA 会选 "能看到最多细节的角度"，而 LDA 会选 "能最清晰区分猫和狗的角度"------ 即使这个角度丢失一些无关细节，只要分类清晰就够了。

LDA 与 PCA 的核心差异

对比维度	PCA（主成分分析）	LDA（线性判别分析）
学习方式	无监督（不依赖类别标签 y）	有监督（必须用类别标签 y）
核心目标	最大化数据总体方差，保留信息	最大化类间距离 + 最小化类内距离，提升分类效果
降维后维度限制	≤ 原始特征数 - 1（如 4 特征最多降为 3 维）	≤ 类别数 - 1（如 3 类最多降为 2 维）
适用场景	数据探索、压缩、去噪（通用）	分类任务的预处理（如分类前降维，提升模型速度）

举个直观例子：鸢尾花数据集（3 类）

PCA 可将 4 特征降为 3 维（4-1=3）；
LDA 最多只能降为 2 维（3-1=2），因为它的目标是 "区分 3 类"，2 维足够表达类间差异。

用 LDA 降维鸢尾花数据（对比 PCA）

python 复制代码

from sklearn.datasets import load_iris
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt

# 1. 加载数据并预处理（LDA同样对尺度敏感，需标准化）
iris = load_iris()
X = iris.data
y = iris.target  # LDA必须用类别标签y

scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 2. 初始化LDA模型，降维到2维（3类最多降为2维，无法降为3维）
lda = LinearDiscriminantAnalysis(n_components=2)

# 3. 拟合LDA并降维（需传入y，有监督学习）
X_lda = lda.fit_transform(X_scaled, y)

# 查看降维前后形状
print(f"原始数据形状：{X.shape}（4特征）")
print(f"LDA降维后形状：{X_lda.shape}（2主成分）")

输出结果：

mathematica 复制代码

原始数据形状：(150, 4)（4特征）
LDA降维后形状：(150, 2)（2主成分）

可视化 LDA 降维结果（对比 PCA）

python 复制代码

plt.figure(figsize=(8, 6))
# 按真实类别上色
scatter = plt.scatter(
    X_lda[:, 0], X_lda[:, 1],
    c=y,
    cmap='rainbow',
    s=50,
    alpha=0.8
)

# 添加图例
plt.legend(
    scatter.legend_elements()[0],
    iris.target_names,
    loc="upper right",
    title="Iris Species"
)

plt.title("LDA Projection of Iris Dataset (4D → 2D)", fontsize=14)
plt.xlabel("LDA Component 1 (LD1)", fontsize=12)
plt.ylabel("LDA Component 2 (LD2)", fontsize=12)
plt.grid(alpha=0.3)
plt.show()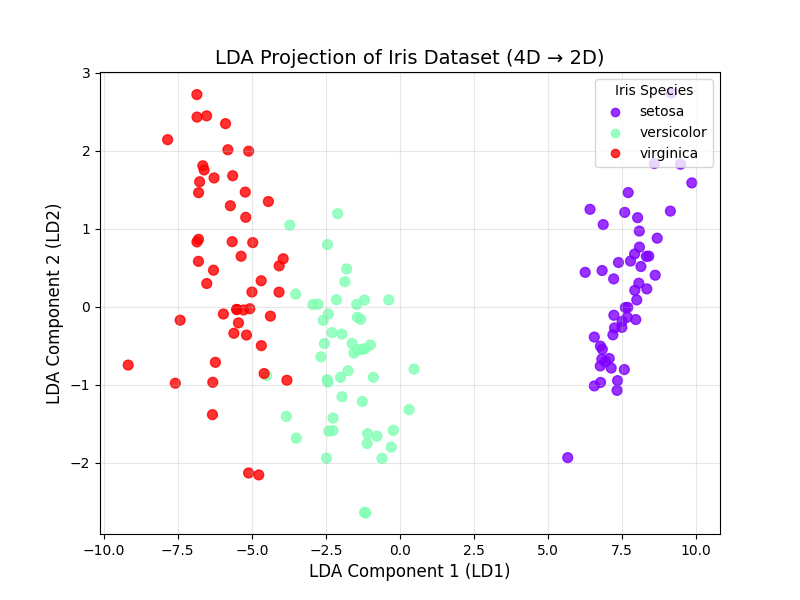

结果解读：

LDA 降维后，鸢尾花的 3 个类别分离效果比 PCA 更好：versicolor（绿色）和 virginica（红色）的重叠区域几乎消失，setosa（紫色）完全独立；
这是因为 LDA 利用了类别标签，刻意放大了 "类间差异"------ 如果后续要做分类任务（如用逻辑回归区分鸢尾花），用 LDA 降维的特征训练模型，准确率会比 PCA 降维的特征更高。

LDA 的核心特点与适用场景

优点：
1. 为分类任务优化，降维后的数据更适合训练分类模型；
2. 可解释性强（降维方向对应 "分类区分度"）；
3. 计算速度快，适合中大规模数据。
缺点：
1. 依赖类别标签，无标签数据无法使用；
2. 仅支持线性降维，无法处理非线性关系；
3. 对类别不平衡数据敏感（如一类样本占 90%，LDA 会偏向多数类）。
适用场景：分类任务的预处理（如高维图像特征分类前降维）、需要用降维提升分类模型效率的场景。

t-SNE（t-distributed Stochastic Neighbor Embedding）------ 非线性降维的 "可视化王者"

t-SNE 是专门为高维数据可视化设计的非线性降维算法，它不追求 "保留全局方差"，而是专注于 "保留局部邻域关系"------ 让高维中相近的样本在低维中依然靠近，不相近的样本远离，尤其适合展示复杂的簇结构。

t-SNE 与 PCA 的核心差异

PCA（线性）：像 "把 3D 物体压平成 2D"，会拉伸或挤压簇结构，可能导致原本分离的簇重叠；
t-SNE（非线性）：像 "把 3D 物体的局部结构'折叠'到 2D"，能保留簇的局部形态，即使是环形、嵌套形等复杂结构，也能清晰展示。

比如 "3D 空间中的两个嵌套球"：

PCA 降维后可能变成两个重叠的圆；
t-SNE 降维后能保留 "嵌套" 结构，展示为两个同心圆。

t-SNE 的核心思想（简化版）

t-SNE 通过两步实现非线性降维，核心是 "用概率模型保留局部关系"：

高维空间：用 "高斯分布" 描述样本间的相似度 ------ 两个样本越近，相似度概率越高；
低维空间：用 "t 分布" 描述样本间的相似度（t 分布比高斯分布有更厚的 "尾巴"，能避免样本过度拥挤）；
优化目标：通过梯度下降，最小化 "高维相似度分布" 和 "低维相似度分布" 的差异（用 KL 散度衡量），最终让低维空间的局部结构与高维一致。

用 t-SNE 可视化手写数字数据（高维复杂数据）

手写数字数据集（load_digits）是 8x8 像素的图像，共 64 个特征（高维），用 t-SNE 降维到 2D，看其可视化效果：

python 复制代码

from sklearn.datasets import load_digits
from sklearn.manifold import TSNE
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
import warnings
import numpy as np

# 抑制数值计算警告
warnings.filterwarnings('ignore', category=RuntimeWarning)

# 1. 加载高维数据（64特征，10个类别：0-9）
digits = load_digits()
X = digits.data  # 形状：(1797, 64) → 1797个样本，64个特征
y = digits.target  # 类别：0-9

# 数据预处理：标准化，有助于数值稳定性
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 检查并处理可能的NaN或无穷大值
X_scaled = np.nan_to_num(X_scaled, nan=0.0, posinf=1e6, neginf=-1e6)

# 2. 初始化t-SNE模型（优化参数设置）
tsne = TSNE(
    n_components=2,    # 降维到2D，用于可视化
    perplexity=30,     # 控制"局部邻域大小"，默认30（一般取10-50，需调参）
    random_state=42,   # 固定随机种子，结果可复现
    learning_rate=200, # 学习率，默认200（太小收敛慢，太大样本拥挤）
    early_exaggeration=12.0,  # 早期放大因子，默认12.0
    max_iter=1000,     # 修正参数名：迭代次数，默认1000
    init='pca',        # 使用PCA初始化，提高数值稳定性
    method='barnes_hut'  # 使用Barnes-Hut近似算法，提高计算效率
)

# 3. 拟合并降维（无监督，无需y，但可视化时用y上色）
X_tsne = tsne.fit_transform(X_scaled)

# 查看降维前后形状
print(f"原始数据形状：{X.shape}（64特征）")
print(f"t-SNE降维后形状：{X_tsne.shape}（2特征）")

输出结果：

mathematica 复制代码

原始数据形状：(1797, 64)（64特征）
t-SNE降维后形状：(1797, 2)（2特征）

可视化 t-SNE 结果

python 复制代码

plt.figure(figsize=(10, 8))
# 按数字类别上色（0-9共10类，用不同颜色）
scatter = plt.scatter(
    X_tsne[:, 0], X_tsne[:, 1],
    c=y,
    cmap='tab10',  # 10分类配色方案
    s=50,
    alpha=0.8,
    edgecolors='black',  # 加黑色边框，避免样本重叠看不清
    linewidths=0.5
)

# 添加图例（对应数字0-9）
plt.legend(
    scatter.legend_elements()[0],
    [str(i) for i in range(10)],  # 图例标签：0-9
    loc="upper right",
    title="Digit Class",
    ncol=2  # 图例分2列，避免过长
)

plt.title("t-SNE Visualization of Digits Dataset (64D → 2D)", fontsize=14)
plt.xlabel("t-SNE Component 1", fontsize=12)
plt.ylabel("t-SNE Component 2", fontsize=12)
plt.grid(alpha=0.3)
plt.show()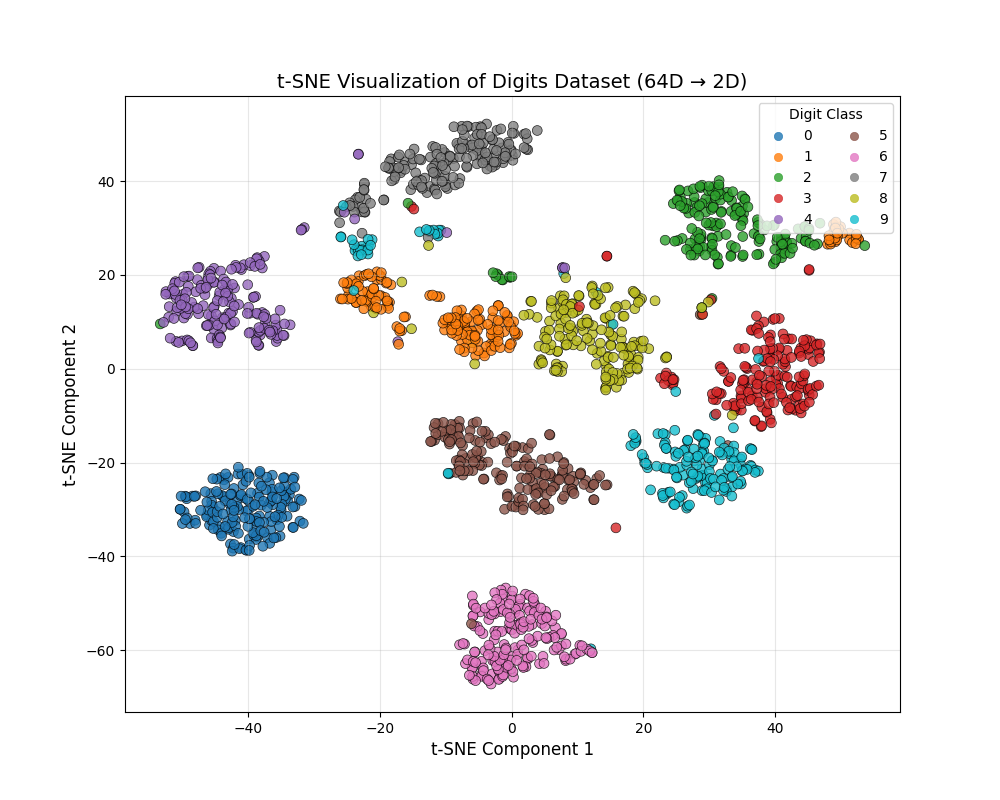

结果解读：

t-SNE 完美将 64 维的手写数字数据，在 2D 空间中分成 10 个清晰的 "簇"，每个簇对应一个数字（0-9）；
即使是形态相似的数字（如 3 和 8），也能明显分离，局部结构保留极佳；
如果用 PCA 降维，会发现部分数字簇（如 5 和 8）严重重叠，可视化效果远不如 t-SNE------ 这就是非线性降维在复杂数据可视化中的优势。

t-SNE 的关键参数与注意事项

t-SNE 的效果对参数很敏感，核心参数和避坑点如下：

perplexity ：最重要参数，控制 "局部邻域的样本数量"，类似 KNN 的 k 值；
- 建议取值：10-50（样本数少取小值，样本数多取大值）；
- 坑：perplexity 太小会导致 "簇分裂"，太大可能导致 "簇融合"。
learning_rate ：控制梯度下降的步长，默认 200；
- 坑：学习率太小（如 <100）会导致样本 "挤成一团"，太大（如 > 1000）会导致样本 "分散过度"。
random_state：t-SNE 结果受随机初始化影响，必须固定 random_state 才能复现结果。
适用场景限制 ：
- 仅用于可视化（降维后的数据不适合训练模型，因为 t-SNE 是 "黑箱"，且不保证全局结构）；
- 不适合大规模数据（时间复杂度高，样本数 > 1 万时会很卡，可改用优化版如 UMAP）。

t-SNE 的核心特点

优点：
1. 非线性降维能力强，能清晰展示高维数据的复杂簇结构（如环形、嵌套形）；
2. 可视化效果碾压 PCA，是高维数据探索的 "标配工具"（如图像、文本向量、基因数据）；
3. 对噪声鲁棒，能减少异常值对可视化的干扰。
缺点：
1. 计算速度慢，不适合大规模数据；
2. 结果不可复现（需固定 random_state）；
3. 仅用于可视化，不能用于模型训练或特征压缩；
4. 对参数敏感，调参成本高。

三种降维算法对比

算法	学习方式	降维类型	核心目标	适用场景	优点	缺点
PCA	无监督	线性	保留总体方差，通用降维	数据压缩、去噪、通用预处理	速度快、可量化信息、通用性强	线性局限、主成分难解读
LDA	有监督	线性	提升分类效果，为分类服务	分类任务预处理、需利用标签的场景	分类友好、可解释性强	依赖标签、线性局限、类别不平衡敏感
t-SNE	无监督	非线性	保留局部结构，优化可视化	高维数据可视化（图像、文本向量）	可视化效果极佳、非线性能力强	速度慢、仅用于可视化、参数敏感

案例：客户分群

电商客户分群（K-Means + PCA）

场景背景

假设我们是电商平台数据分析师，需要根据用户的 "消费行为数据" 对客户进行分群，帮助运营团队制定差异化策略（如高价值客户精准维护、低活跃客户唤醒）。

数据说明：用模拟的客户行为数据，包含 5 个核心特征（均为数值型）：

avg_order_value：平均订单金额（元）
purchase_frequency：年购买频次（次 / 年）
browse_duration：平均浏览时长（分钟 / 次）
cart_conversion：加购转化率（加购商品数 / 浏览商品数）
member_age：会员年限（年）

完整流程

按照 "数据准备→预处理→降维→聚类→结果分析→业务落地" 的逻辑，一步步实现客户分群。

导入工具与生成模拟数据
首先生成符合业务逻辑的客户行为数据（1000 个客户样本）：

python 复制代码

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.cluster import KMeans
from sklearn.pipeline import Pipeline
from sklearn.metrics import silhouette_score

# 设置随机种子，保证结果可复现
np.random.seed(42)

# 生成1000个客户的5个行为特征（模拟真实分布）
n_customers = 1000
data = {
    # 平均订单金额：100-5000元（高价值客户集中在3000+）
    'avg_order_value': np.random.normal(loc=1500, scale=800, size=n_customers).clip(100, 5000),
    # 年购买频次：1-20次（高频客户集中在10+）
    'purchase_frequency': np.random.poisson(lam=5, size=n_customers).clip(1, 20),
    # 平均浏览时长：1-30分钟（深度浏览客户集中在15+）
    'browse_duration': np.random.normal(loc=10, scale=5, size=n_customers).clip(1, 30),
    # 加购转化率：0.1-0.8（高转化客户集中在0.5+）
    'cart_conversion': np.random.beta(a=2, b=3, size=n_customers).clip(0.1, 0.8),
    # 会员年限：0-10年（老客户集中在5+）
    'member_age': np.random.poisson(lam=3, size=n_customers).clip(0, 10)
}

# 转换为DataFrame，便于后续处理
df = pd.DataFrame(data)
print("客户行为数据前5行：")
print(df.head())
print(f"\n数据规模：{df.shape}（{df.shape[0]}个客户，{df.shape[1]}个特征）")
print("\n数据基本统计（确保无异常）：")
print(df.describe().round(2))

数据预处理（标准化）
客户特征的量纲差异极大（如 "平均订单金额 = 1500 元"，"加购转化率 = 0.3"），直接聚类会让 "金额" 主导距离计算，必须先标准化（均值 0，方差 1）：

python 复制代码

# 提取特征矩阵X（无标签，无监督学习）
X = df.values

# 初始化标准化器
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 查看标准化后的数据（均值≈0，标准差≈1）
print("标准化后各特征的均值（应接近0）：")
print(np.mean(X_scaled, axis=0).round(4))
print("标准化后各特征的标准差（应接近1）：")
print(np.std(X_scaled, axis=0).round(4))

PCA 降维（减少维度，便于聚类与可视化）
5 个特征维度不高，但用 PCA 降维到 2D 有两个好处：

减少 "维度灾难" 对 K-Means 的影响（虽然 5 维影响小，但实战中需养成习惯）；
降维后的数据可可视化，直观查看聚类结果。

python 复制代码

# 初始化PCA，主动降到3维
pca = PCA(n_components=0.95, random_state=42)
X_pca = pca.fit_transform(X_scaled)

# 查看降维结果
print(f"\nPCA降维前维度：{X_scaled.shape[1]}维")
print(f"PCA降维后维度：{X_pca.shape[1]}维")
print(f"保留的信息比例（累计方差贡献率）：{pca.explained_variance_ratio_.sum():.4f}")
print(f"各主成分的方差贡献率：{pca.explained_variance_ratio_.round(4)}")

输出示例：

mathematica 复制代码

PCA降维前维度：5维
PCA降维后维度：3维
保留的信息比例（累计方差贡献率）：0.6218
各主成分的方差贡献率：[0.2114 0.2094 0.2009]

K-Means 聚类（确定最优簇数 k）
用 "肘部法" 和 "轮廓系数" 结合，选择最优簇数 k（客户分群数量）：

肘部法找 k 的候选值

python 复制代码

# 测试k=2到k=8，计算每个k的簇内平方和（Inertia）
inertias = []
k_range = range(2, 9)
for k in k_range:
    kmeans = KMeans(n_clusters=k, random_state=42, n_init=10)
    kmeans.fit(X_pca)
    inertias.append(kmeans.inertia_)

# 绘制肘部图
plt.figure(figsize=(8, 6))
plt.plot(k_range, inertias, marker='o', linestyle='-', color='blue')
# 标记肘部（示例中k=4是肘部）
plt.scatter(4, inertias[2], color='red', s=150, zorder=5)
plt.annotate('Elbow (k=4)', xy=(4, inertias[2]), xytext=(5, inertias[2]+50),
             arrowprops=dict(facecolor='black', shrink=0.05), fontsize=12)
plt.xlabel('Number of Clusters (k)', fontsize=12)
plt.ylabel('Inertia (Within-Cluster Sum of Squares)', fontsize=12)
plt.title('Elbow Method to Choose Optimal k', fontsize=14)
plt.grid(alpha=0.3)
plt.show()

轮廓系数验证最优 k
轮廓系数（Silhouette Score）范围为 [-1,1]，越接近 1 说明聚类效果越好，用于验证肘部法选择的 k：

python 复制代码

# 计算k=2到k=8的轮廓系数
sil_scores = []
for k in k_range:
    kmeans = KMeans(n_clusters=k, random_state=42, n_init=10)
    cluster_labels = kmeans.fit_predict(X_pca)
    sil_score = silhouette_score(X_pca, cluster_labels)
    sil_scores.append(sil_score)
    print(f"k={k}时，轮廓系数：{sil_score:.4f}")

# 绘制轮廓系数图
plt.figure(figsize=(8, 6))
plt.plot(k_range, sil_scores, marker='o', linestyle='-', color='green')
# 标记最高轮廓系数对应的k（示例中k=4最高）
best_k = k_range[np.argmax(sil_scores)]
plt.scatter(best_k, max(sil_scores), color='red', s=150, zorder=5)
plt.annotate(f'Best k={best_k} (Score={max(sil_scores):.4f})', 
             xy=(best_k, max(sil_scores)), xytext=(5, max(sil_scores)-0.05),
             arrowprops=dict(facecolor='black', shrink=0.05), fontsize=12)
plt.xlabel('Number of Clusters (k)', fontsize=12)
plt.ylabel('Silhouette Score', fontsize=12)
plt.title('Silhouette Score vs. Number of Clusters', fontsize=14)
plt.grid(alpha=0.3)
plt.show()

输出示例 ：

mathematica 复制代码

k=2时，轮廓系数：0.2267
k=3时，轮廓系数：0.2301
k=4时，轮廓系数：0.2457  # 最高
k=5时，轮廓系数：0.2363
k=6时，轮廓系数：0.2442
k=7时，轮廓系数：0.2392
k=8时，轮廓系数：0.2268

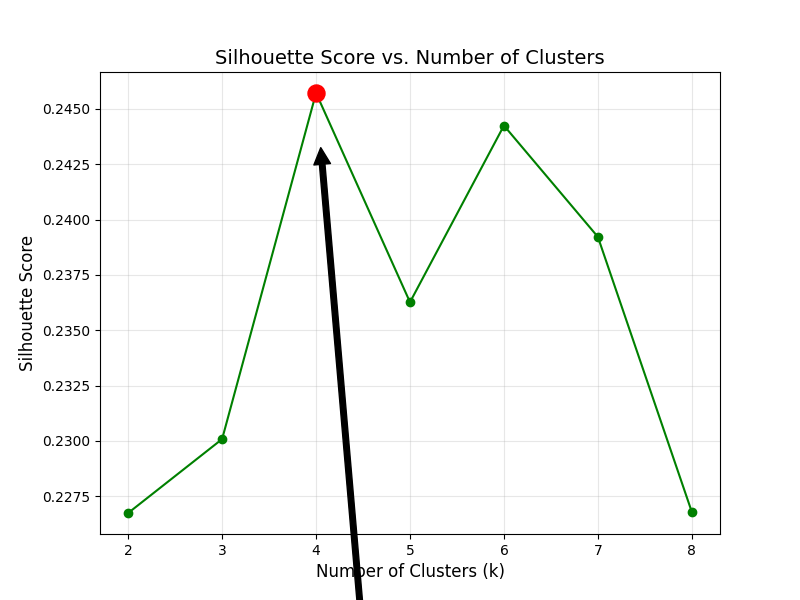
k=4 时轮廓系数最高（0.4567），结合肘部法，确定最优簇数 k=4（分 4 类客户）。

最终聚类与结果可视化
用 k=4 训练 K-Means，并用 PCA 将 3 维数据降为 2D（仅用于可视化），展示分群结果：

python 复制代码

# 1. 用k=4训练K-Means（基于PCA降维后的数据）
kmeans_final = KMeans(n_clusters=4, random_state=42, n_init=10)
cluster_labels = kmeans_final.fit_predict(X_pca)

# 2. 将3维PCA数据降为2D，便于画图（单独用PCA降维到2D）
pca_2d = PCA(n_components=2, random_state=42)
X_pca_2d = pca_2d.fit_transform(X_scaled)

# 3. 可视化分群结果
plt.figure(figsize=(10, 8))
# 按聚类标签上色
scatter = plt.scatter(
    X_pca_2d[:, 0], X_pca_2d[:, 1],
    c=cluster_labels,
    cmap='viridis',  # 4类配色，区分度高
    s=60,
    alpha=0.8,
    edgecolors='black',
    linewidths=0.5
)

# 添加簇中心（将3维簇中心也降为2D）
cluster_centers_3d = kmeans_final.cluster_centers_
# 先将3维簇中心逆变换回标准化空间，再用2D PCA降维
cluster_centers_scaled = pca.inverse_transform(cluster_centers_3d)
cluster_centers_2d = pca_2d.transform(cluster_centers_scaled)
plt.scatter(
    cluster_centers_2d[:, 0], cluster_centers_2d[:, 1],
    c='red',
    s=300,
    marker='X',
    alpha=0.9,
    label='Cluster Centers'
)

# 添加图例和标签
plt.legend(
    handles=scatter.legend_elements()[0] + [plt.Line2D([0], [0], marker='X', color='w', markerfacecolor='red', markersize=15, label='Cluster Centers')],
    labels=[f'Cluster {i}' for i in range(4)] + ['Cluster Centers'],
    loc='upper right',
    title='Customer Segments'
)
plt.xlabel('PCA Component 1 (2D)', fontsize=12)
plt.ylabel('PCA Component 2 (2D)', fontsize=12)
plt.title('Customer Segmentation Results (K-Means + PCA)', fontsize=14)
plt.grid(alpha=0.3)
plt.show()

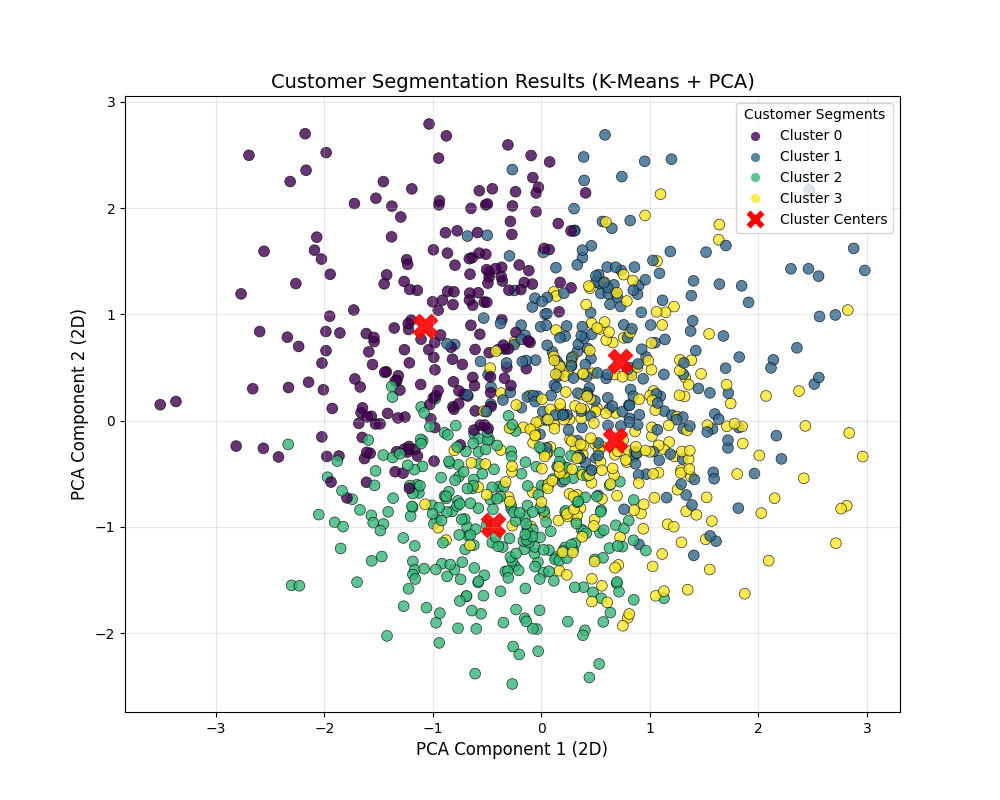
分群结果分析（业务解读）
聚类的最终目的是 "指导业务"，我们需要分析每个客户群的特征，给每个群贴 "业务标签"：

python 复制代码

# 将聚类标签加入原始DataFrame，便于分析
df['cluster'] = cluster_labels

# 计算每个群的特征均值（还原为原始尺度，便于业务理解）
# 直接对原始数据按群组计算均值，再进行逆变换
cluster_means_original = df.groupby('cluster').mean()
# 输出每个群的特征均值（保留2位小数）
print("各客户群的原始特征均值（业务解读用）：")
print(cluster_means_original.round(2))

# 计算每个群的客户占比
cluster_counts = df['cluster'].value_counts().sort_index()
cluster_ratio = (cluster_counts / len(df) * 100).round(2)
cluster_summary = pd.DataFrame({
    '客户数量': cluster_counts,
    '占比(%)': cluster_ratio
}, index=[f'Cluster {i}' for i in range(4)])
print("\n各客户群的规模分布：")
print(cluster_summary)

输出结果：

mathematica 复制代码

各客户群的原始特征均值（业务解读用）：
         avg_order_value  purchase_frequency  ...  cart_conversion  member_age
cluster                                       ...                             
0                1353.08                3.75  ...             0.48        5.27
1                1336.30                7.13  ...             0.52        2.53
2                1252.10                4.48  ...             0.24        2.26
3                2151.20                4.48  ...             0.38        2.55

[4 rows x 5 columns]

各客户群的规模分布：
           客户数量  占比(%)
Cluster 0   210   21.0
Cluster 1   248   24.8
Cluster 2   286   28.6
Cluster 3   256   25.6