CNN(卷积神经网络)和 RNN(循环神经网络)是深度学习中两种针对不同数据类型设计的网络结构
CNN(卷积神经网络)
核心机制:通过卷积操作和池化操作处理数据,依赖局部感受野(局部感受野,Local Receptive Field)和参数共享
卷积层:用卷积核提取局部特征(如图像中的边缘、纹理),每个卷积核只关注输入的局部区域(局部感受野),且同一卷积核在输入上滑动时参数复用(参数共享),大幅减少计算量
池化层:对特征图降维,保留关键信息,增强平移不变性(如图像中物体轻微移动不影响识别)
数据假设:输入数据具有空间局部相关性(如像素相邻的图像、网格结构的音频频谱图),且元素顺序对局部特征影响不大(如图像中 "左上角像素" 和 "右上角像素" 无强依赖)
RNN(循环神经网络)
核心机制:通过循环连接处理数据,依赖时序记忆
网络中包含 "循环单元"(如 Simple RNN、LSTM、GRU),每个时刻的输出不仅依赖当前输入,还依赖上一时刻的隐藏状态(即 "记忆")
例如,处理句子 "我喜欢吃____" 时,"喜欢吃" 的信息会被保存在隐藏状态中,帮助预测最后一个词(如 "苹果")
数据假设:输入数据是序列结构(如文本、时间序列),元素顺序至关重要(如 "我爱你" 和 "你爱我" 语义完全不同),且存在长距离时序依赖(如文本中前文对后文的语义影响)
关键区别
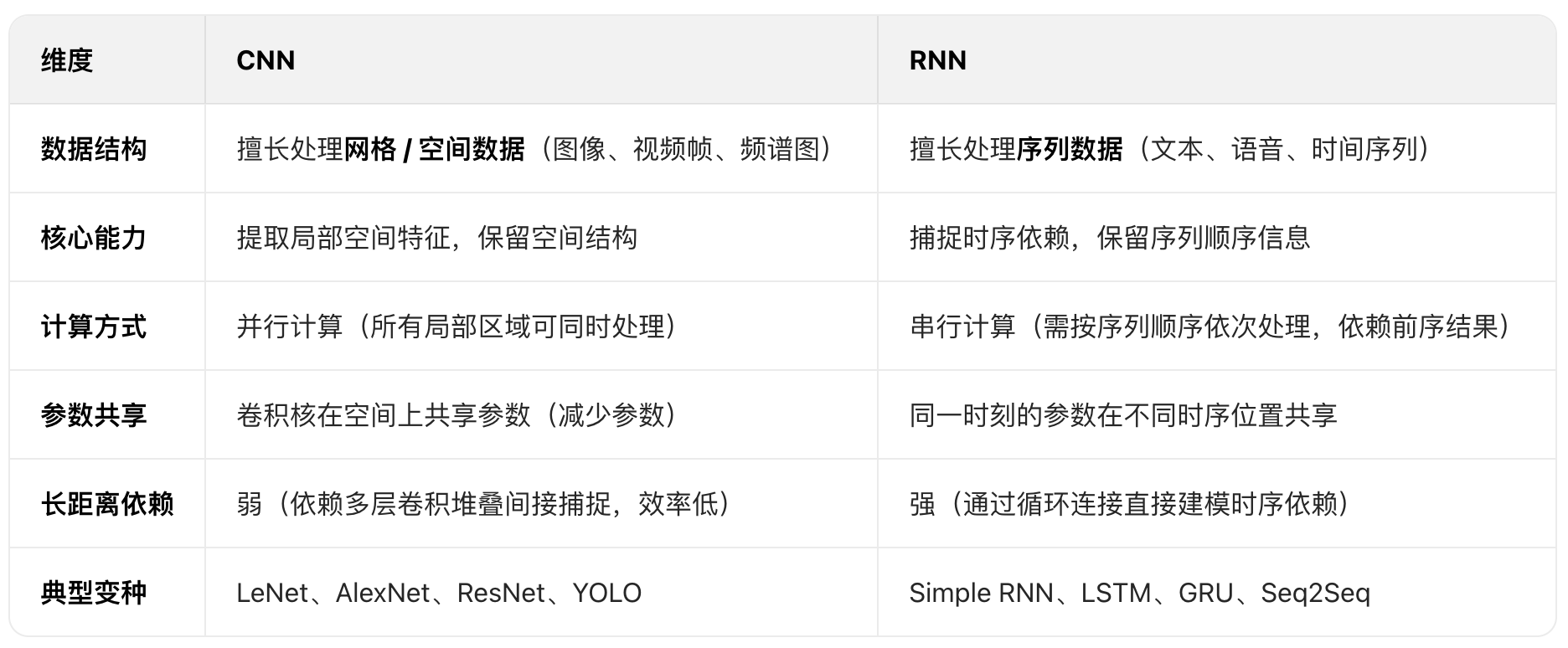
举例说明
CNN 的典型应用:图像分类(以识别 "猫" 为例)
输入:一张 224×224 的 RGB 图像(张量形状 (1, 224, 224, 3))
处理过程:
第一层卷积:用多个 3×3 卷积核提取边缘特征(如猫的轮廓边缘、耳朵边缘),输出特征图(每个通道对应一种边缘)。
池化层:对特征图降维(如 2×2 最大池化,尺寸变为 112×112),保留最强边缘信息。
深层卷积:堆叠更多卷积层,逐步提取复杂特征(如猫的眼睛、鼻子、毛发纹理),最终通过全连接层输出 "是否为猫" 的分类结果。
为何用 CNN:图像的像素具有局部相关性(相邻像素构成边缘 / 纹理),CNN 的局部感受野能高效捕捉这些特征,且参数共享大幅降低计算量。
RNN 的典型应用:文本情感分析(判断句子 "这部电影太精彩了!" 的情感)
输入:
分词后的序列 ["这部", "电影", "太", "精彩", "了", "!"]
每个词转为词向量,张量形状 (1, 6, d_model),d_model 为词向量维度
处理过程:
初始隐藏状态 h0 为全 0 向量
第一个词 "这部" 输入 RNN 单元,结合 h0 计算隐藏状态 h1(记录 "这部" 的信息)
第二个词 "电影" 输入,结合 h1 计算 h2(记录 "这部电影" 的信息)
依次处理后续词,最终隐藏状态 h6 融合了整个句子的信息,通过全连接层输出 "正面情感" 的结果
为何用 RNN:
文本的语义依赖词的顺序("精彩" 是关键词,且需结合前文 "电影" 才能判断情感)
RNN 的循环连接能记住前序词的信息,捕捉这种时序依赖
总结
CNN 是 "空间特征提取器":适合处理图像、视频等具有局部空间相关性的数据,通过卷积和池化高效提取层次化特征
RNN 是 "时序记忆器":适合处理文本、语音等序列数据,通过循环连接捕捉时序依赖,记住前序信息
实际应用两者可结合(如视频分析:用 CNN 提取每一帧的图像特征,再用 RNN 处理帧序列的时序关系)
局部感受野(Local Receptive Field)
定义
是指卷积核在输入张量上每次操作时所覆盖的局部区域
它是 CNN 高效提取局部特征的核心机制,类比于生物视觉系统中单个神经元仅对视野中局部区域刺激产生反应的特性。
卷积核的尺寸直接决定了局部感受野的大小。例如:
- 一个 3×3 的卷积核,其局部感受野就是 3×3 的区域(每次滑动时覆盖输入的 3 行 3 列像素)
- 一个 5×5 的卷积核,局部感受野则是 5×5 的区域
多层CNN网络的感受野扩张
在深层 CNN 中,随着卷积层的堆叠,单个输出特征的感受野会逐渐扩大。例如:
- 第一层 3×3 卷积的感受野是 3×3
- 第二层 3×3 卷积的感受野会扩展到 5×5(因为它的输入是第一层的 3×3 特征图,相当于覆盖了原始输入的 5×5 区域)
- 以此类推,深层特征可以捕捉更大范围的上下文信息
每个卷积层的输出特征,本质是对前一层特征的局部聚合;而前一层的特征又对应更前一层的局部区域
因此,深层特征的每个点,会间接关联到原始输入中更大的区域,这个区域就是它的 "感受野"
逐层推导(以 3×3 卷积核、步长 = 1、无填充为例)
假设输入是一张 10×10 的原始图像(简化为单通道),堆叠 3 层 3×3 卷积,看看每层输出特征的感受野如何变化
第 1 层卷积(Conv1):感受野 = 3×3
输入:10×10 的原始图像(记为 Input)
卷积核:3×3(每次覆盖 Input 的 3×3 区域)
输出:8×8 的特征图(Conv1_out,因为 10-3+1=8)
感受野计算:
Conv1_out 上的每个点,只由 Input 中 3×3 的区域计算得到(比如 Conv1_out 的 (0,0) 点,对应 Input 的 (0,0)~(2,2) 区域)Conv1 的感受野 = 3×3
第 2 层卷积(Conv2):感受野 = 5×5
输入:Conv1_out(8×8 的特征图,每个点对应 Input 的 3×3 区域)
卷积核:3×3(每次覆盖 Conv1_out 的 3×3 区域)
输出:6×6 的特征图(Conv2_out,8-3+1=6)
感受野计算:
Conv2_out 上的每个点,是对 Conv1_out 中 3×3 的点进行聚合
而这 3×3 的每个点,又分别对应 Input 中 3×3 的区域
例如:Conv2_out 的 (0,0) 点,来自 Conv1_out 的 (0,0)、(0,1)、(0,2)、(1,0)、(1,1)、(1,2)、(2,0)、(2,1)、(2,2) 这 9 个点
这 9 个点在 Input 中对应的区域是:
(0,0)~(2,2)(来自 Conv1_out (0,0))
(0,1)~(2,3)(来自 Conv1_out (0,1))
...
(2,2)~(4,4)(来自 Conv1_out (2,2))
这些区域合并后,覆盖 Input 的 (0,0)~(4,4)(共 5×5)
Conv2 的感受野 = 5×5
第 3 层卷积(Conv3):感受野 = 7×7
输入:Conv2_out(6×6 的特征图,每个点对应 Input 的 5×5 区域)
卷积核:3×3(每次覆盖 Conv2_out 的 3×3 区域)
输出:4×4 的特征图(Conv3_out,6-3+1=4)
感受野计算:
Conv3_out 的每个点,是对 Conv2_out 中 3×3 的点聚合。而这 3×3 的每个点,对应 Input 的 5×5 区域。合并后,覆盖 Input 的 (0,0)~(6,6)(共 7×7)
Conv3 的感受野 = 7×7
规律总结:
每增加一层 3×3 卷积(步长 = 1),感受野的边长会增加 2(即 3→5→7→...)
公式:第 n 层 3×3 卷积的感受野边长 = 1 + 2×n(n 为层数)
这就是为什么 "深层特征能捕捉更大范围的上下文信息":
- 浅层(如第 1 层)只能看到图像的局部细节(如边缘、纹理)
- 深层(如第 3 层)能看到更大的区域(如物体的一部分)
- 堆叠更多层后,感受野可覆盖整个图像,从而理解全局语义(如 "这是一只猫")
形象类比
想象站在高楼里看地面:
1 楼(浅层):只能看到窗外 3×3 米的地砖
2 楼(中层):能看到 5×5 米的区域(包括楼下看到的地砖和旁边的区域)
10 楼(深层):能看到整个小区的布局
每层 "视野"(感受野)的扩大,就是因为 "站在下层的视野上" 再往外看,这和 CNN 堆叠卷积层的原理完全一致
为什么说像素相邻的图像、网格结构的音频频谱图具有空间局部相关性
这个问题问到了 CNN 能高效处理这类数据的核心逻辑 ------"空间局部相关性" 本质是指数据在空间(或网格)上相邻的元素,其语义或特征高度相关,而非相邻元素的关联性较弱。我们可以通过图像和音频频谱图两个具体例子,拆解这种相关性的来源:
先理解 "空间局部相关性" 的核心:相邻元素 "同属一个特征"
无论是图像的像素还是音频频谱图的网格点,它们的 "空间位置" 不是随机的
相邻的点往往共同构成一个有意义的局部特征
距离远的点则属于不同特征
就像拼图:相邻的拼图块共同组成图案的一部分,远的拼图块则属于完全不同的区域
举例 1:图像的像素为何有空间局部相关性?
图像的本质是 "光信号的空间分布",人眼能识别的特征(边缘、纹理、形状)都是由相邻像素共同构成的
具体体现在 3 个方面:
边缘特征依赖相邻像素比如一张 "黑色背景上的白色直线" 图像:
直线边缘处的像素,左边是白色(像素值 255)、右边是黑色(像素值 0)------ 这两个相邻像素的差异,正是 "边缘" 的定义。如果这两个像素不相邻(比如中间隔了多个灰色像素),就无法形成清晰的边缘。
结论:"边缘" 这个局部特征,必须由相邻像素的明暗差异来体现,非相邻像素(如直线左边和背景右边的像素)毫无关联。
纹理特征依赖相邻像素比如 "草地" 的纹理:相邻的像素都是绿色(只是深浅略有差异),共同构成 "草地" 的局部质感;而草地旁边 "天空" 的像素是蓝色,相邻的蓝色像素共同构成 "天空" 的质感。
结论:"纹理" 是相邻像素颜色 / 亮度的规律变化,远的像素(如草地和天空的像素)颜色差异大,无关联。
物体形状依赖相邻像素比如 "圆形苹果":苹果边缘的像素会形成连续的曲线 ------ 每个像素的位置都和旁边的像素紧密衔接,共同构成 "圆形" 的轮廓;而苹果内部的像素都是红色 / 黄色,相邻像素颜色一致,共同构成 "苹果主体"。
结论:"形状" 是相邻像素空间位置的连续排列,远的像素(如苹果和桌子的像素)属于不同物体,无关联。
举例 2:音频频谱图的网格为何有空间局部相关性?
音频频谱图是 "声音信号的时空 - 频率网格",先理解它的结构:
横轴:时间(从左到右是声音的流逝)
纵轴:频率(从下到上是声音的高低,比如低音到高音)
像素值:声音的强度(颜色越深,声音越大)
它的空间局部相关性来自 "声音的物理特性"------相邻时间、相邻频率的声音,往往属于同一个音素 / 音符
具体体现在 2 个方面:
同一音符的频率集中在相邻网格比如钢琴弹一个 "中央 C"(频率约 261.6Hz):这个音符的能量不会只集中在 261.6Hz 这一个频率点,而是会扩散到相邻的频率(如 250Hz~270Hz)
这些相邻的频率网格点,共同构成 "中央 C" 这个音符的频谱特征。→ 结论:"单个音符" 的能量分布在相邻的频率网格,远的频率(如 261.6Hz 和 1000Hz)属于不同音符,无关联。
同一音素的时间集中在相邻网格比如人说 "啊" 这个音素:
发音持续 0.5 秒,在频谱图上就是横轴上连续 0.5 秒的网格点
这些相邻时间的网格点,都呈现 "低频能量强、高频能量弱" 的特征,共同构成 "啊" 的声音特征;0.5 秒后说的 "哦",时间上不相邻,频谱特征完全不同。
结论:"单个音素" 的特征分布在相邻的时间网格,远的时间(如 "啊" 和 "哦" 的时间点)属于不同音素,无关联。
总结
正是因为 "空间局部相关性"------ 相邻元素共同构成局部特征,CNN 的局部感受野(卷积核只覆盖相邻元素)才能精准捕捉这些特征:
- 对图像:用 3×3 卷积核覆盖相邻像素,直接提取边缘、纹理
- 对音频频谱图:用 3×3 卷积核覆盖 "相邻时间 + 相邻频率" 的网格,直接提取音符、音素
如果用 "全局感受野"(如全连接层)处理,会把 "相邻的相关元素" 和 "远的无关元素" 混在一起计算,既浪费算力,又会提取到错误的特征(比如把苹果和桌子的像素强行关联)