文章目录
- 一、数组
-
- [ 1、数组:](# 1、数组:)
- [ 2、、数组的顺序存储](# 2、、数组的顺序存储)
-
- [ 1)、一维数组的存储与地址计算](# 1)、一维数组的存储与地址计算)
- [ 2)、二维数组的存储与地址计算](# 2)、二维数组的存储与地址计算)
- [ 3)、三维数组的存储与地址计算](# 3)、三维数组的存储与地址计算)
- [ 4)、N维数组的通用地址公式](# 4)、N维数组的通用地址公式)
- 二、矩阵
-
- [ 1、矩阵](# 1、矩阵)
- [ 2、特殊矩阵](# 2、特殊矩阵)
-
- [ 对称矩阵:](# 对称矩阵:)
- [ 上(下)三角矩阵:](# 上(下)三角矩阵:)
- [ 三对角矩阵:](# 三对角矩阵:)
- [ 3、稀疏矩阵:](# 3、稀疏矩阵:)
-
- [ 稀疏矩阵:](# 稀疏矩阵:)
- [ 三元组表示法:](# 三元组表示法:)
- [ 邻接表表示法:](# 邻接表表示法:)
- [ 十字链表表示法:](# 十字链表表示法:)
- 三、广义表
-
- [ 1、相关概念](# 1、相关概念)
- [ 2、广义表的实例](# 2、广义表的实例)
- [ 3、广义表的存储结构](# 3、广义表的存储结构)
-
- [ 头尾链表存储结构:](# 头尾链表存储结构:)
- [ 扩展线性表存储结构:](# 扩展线性表存储结构:)
一、数组
1、数组:
数组是存储在连续内存空间中的相同类型元素的集合。
维度: 数组可以是一维(如列表)、二维(如表格)、三维或更高维。
索引: 每个元素通过下标(索引)访问,如 A[i](一维)、B[i][j](二维)。
2、、数组的顺序存储
1)、一维数组的存储与地址计算
存储方式:
一维数组在内存中是连续存放的。
例如:int A[5] = {10, 20, 30, 40, 50} 的内存布局如下:
地址: A+0 A+4 A+8 A+12 A+16
值: [10] [20] [30] [40] [50]
地址计算
元素 A[i] 的地址公式:
address(A[i]) = 基地址 + i × 元素大小
基地址:数组首元素地址(如 A 或 A+0)。
i:索引(从0开始)。
元素大小:如 int 为4字节,double 为8字节。
例子:
A[2] 的地址 = A + 2×4 = A + 8(对应值30)。
2)、二维数组的存储与地址计算
存储方式
二维数组有两种存储方式:
行优先(Row-major):
先存第一行,再存第二行...(C/C++、Python默认)。
列优先(Column-major):
先存第一列,再存第二列...(Fortran、MATLAB默认)。
以 int B[3][4] 为例:
行优先存储:
B[0][0], B[0][1], B[0][2],B[0][3],B[1][0], B[1][1], ..., B[2][3]
列优先存储:
B[0][0], B[1][0], B[2][0],B[0][1], B[1][1], ..., B[2][3]
行优先地址计算
元素 B[i][j] 的地址公式:
address(B[i][j]) = 基地址 + (i × 列数 + j) × 元素大小
列数:第二维的大小(如 B[3][4] 的列数是4)。
列优先地址计算
元素 B[i][j] 的地址公式:
address(B[i][j]) = 基地址 + (j × 行数 + i) × 元素大小
行数:第一维的大小(如 B[3][4] 的行数是3)。
3)、三维数组的存储与地址计算
以 int C[2][3][4] 为例(维度:2×3×4)。
行优先存储
内存顺序:
C[0][0][0], C[0][0][1], ..., C[0][0][3],
C[0][1][0], ..., C[0][2][3],
C[1][0][0], ..., C[1][2][3]
地址计算
元素 C[i][j][k] 的地址公式:
address(C[i][j][k]) = 基地址 + (i×3×4 + j×4 + k) × 元素大小
i:第一维索引。
j:第二维索引。
k:第三维索引。
3×4:第二维和第三维的乘积(即一个 i 的偏移量)。
例子:
C[1][2][3] 的地址 = C + (1×12 + 2×4 + 3)×4 = C + (12+8+3)×4 = C + 92。
4)、N维数组的通用地址公式
对于N维数组 A[d1][d2][d3]...[dn],元素 A[i1][i2][i3]...[in] 的地址:
行优先存储
address = 基地址 + (i1×d2×d3×...×dn + i2×d3×...×dn + ... + in-1×dn + in) × 元素大小。
规律:
第一维 i1 乘以后面所有维度大小的乘积(d2×d3×...×dn)。
第二维 i2 乘以后面所有维度大小的乘积(d3×...×dn)。
最后一维 in 直接相加。
列优先存储
address = 基地址 + (in×d1×d2×...×dn-1 + ... + i2×d1 + i1) × 元素大小
(与行优先相反,从最后一维开始计算)
二、矩阵
1、矩阵
由 m × n 个数aij排成的m行n列的数表称为m行n列的矩阵,简称m × n矩阵。

2、特殊矩阵
对称矩阵:
矩阵中的元素满足 A(i,j)=A(j,i),的矩阵称之为对称矩阵(矩阵必须是方阵)。

上(下)三角矩阵:
三角矩阵是方形矩阵的一种,因其非零系数的排列呈三角形状而得名。
三角矩阵分上三角矩阵和下三角矩阵两种。

三对角矩阵:
非零元素仅出现在主对角线及其紧邻的上下两条对角线(即"次对角线")上,其他所有位置的元素均为零的矩阵。

3、稀疏矩阵:
稀疏矩阵:
矩阵中绝大多数元素都为零的矩阵。

三元组表示法:
三元组表示法是使用一个三元组 (i, j, value)单位,表示一个稀疏矩阵。
其中 i表示非零元素所在的行号,j表示其列号,value是该元素的值 。
通常,所有非零元素的三元组会按照行优先的顺序存储在一个一维数组或列表中。

第一行为非零元素个数,第二为行数,第三为列数。

邻接表表示法:

十字链表表示法:
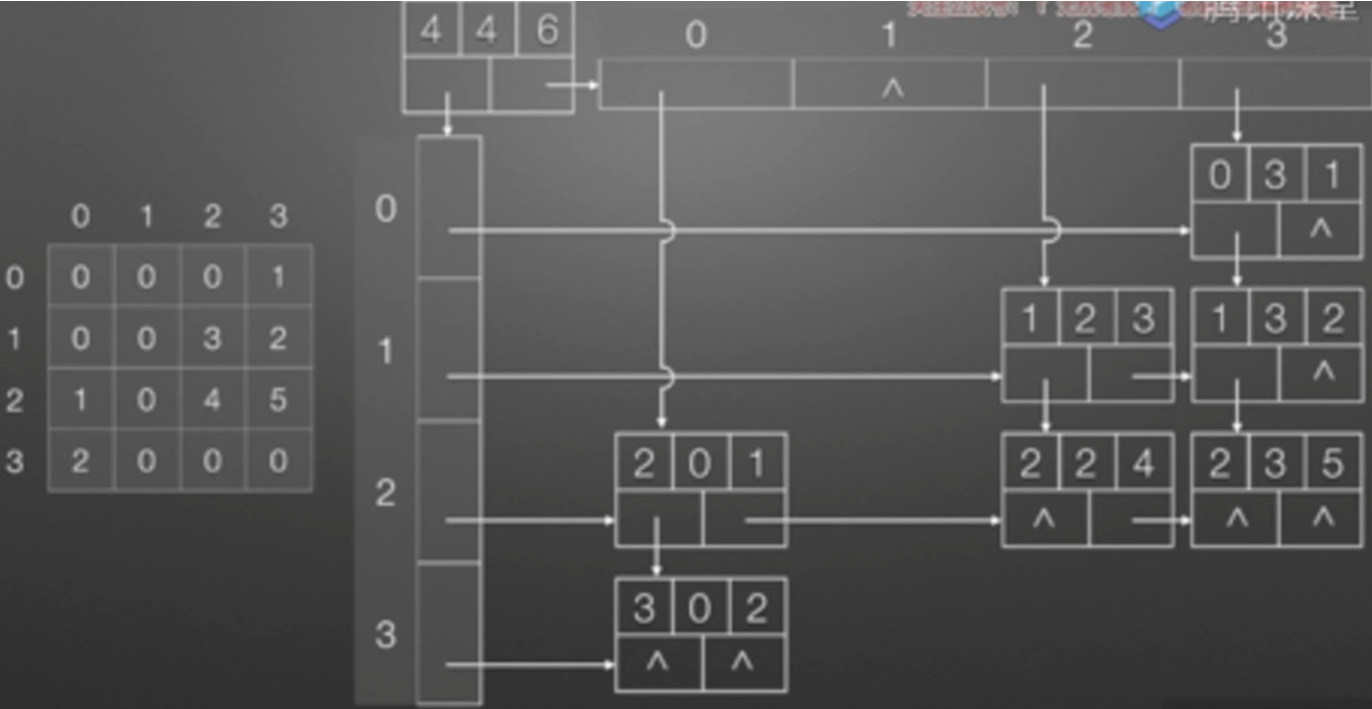
三、广义表
1、相关概念
广义表:n个表元素组成的有限序列,GL = (d0, d1, ..., dn-1) GL是表名,d为表元素。
表头(head):表中第一个元素,GetHead()取表头 。
表尾(tail):表中最后一个元素,GetTail()取表尾。
长度:最外层包含元素的个数。
深度:最大所含括弧的重数。

2、广义表的实例
A=(),A是一个空表,长度为0,深度为1.
B=(d,e),B的元素全是原子,d和e,长度为2,深度为1。
C=(b,(c.d)),C有两个元素,分别是原子b 和另一个广义表(c.d),长度为2,深度为2。
D=(B,C),D的元素全是广义表,B和C,长度为2,深度为3,由此可见一个广义表的子表可以是其他已经定义的广义表的引用。
E=(a,E),E有两个元素,原子a和它本身,长度为2,由此可见一个广义表可以是递归定义的。展开E可以得到(a,(a,(a,(a,.)))),是一个无限深的广义表。
3、广义表的存储结构
头尾链表存储结构:
A=():
A=NULL;
B=(d,e):
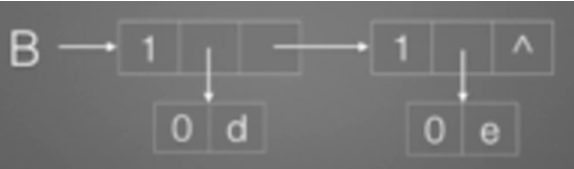
C=(b,(c.d)):
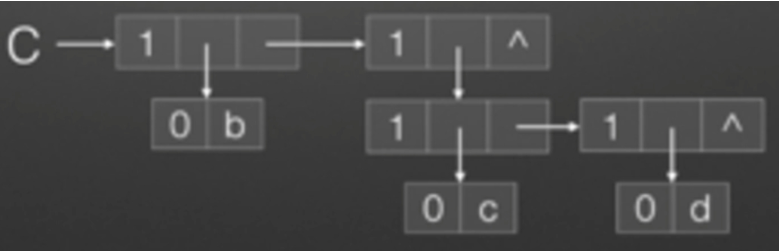
D=(B,C):
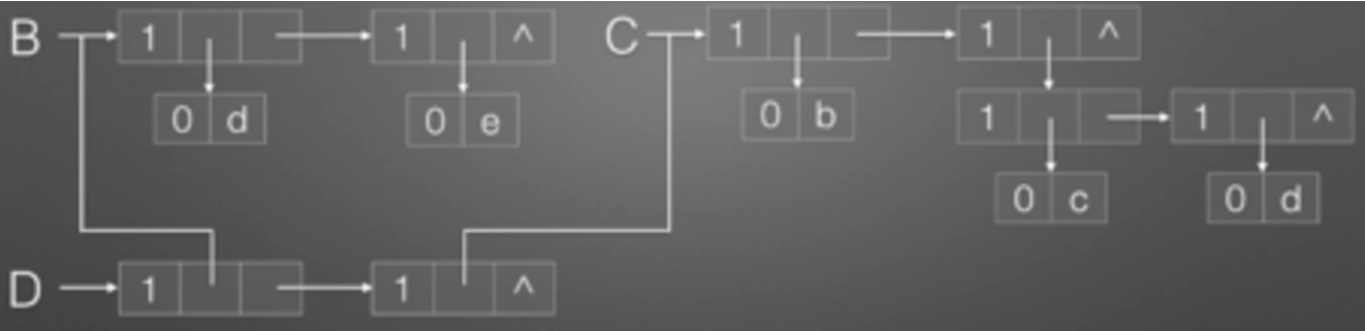
E=(a,E):
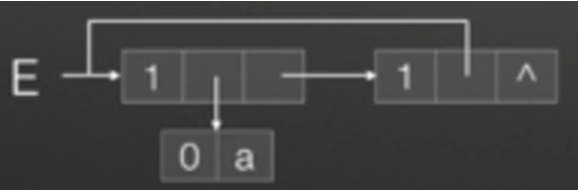
扩展线性表存储结构:
A=():

B=(d,e):

C=(b,(c.d)):

D=(B,C):
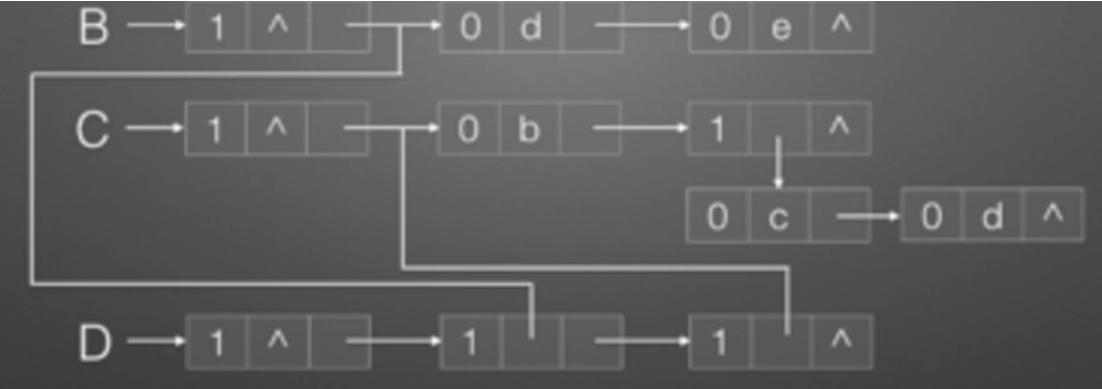
E=(a,E):
