代码随想录 701.二叉搜索树中的插入操作

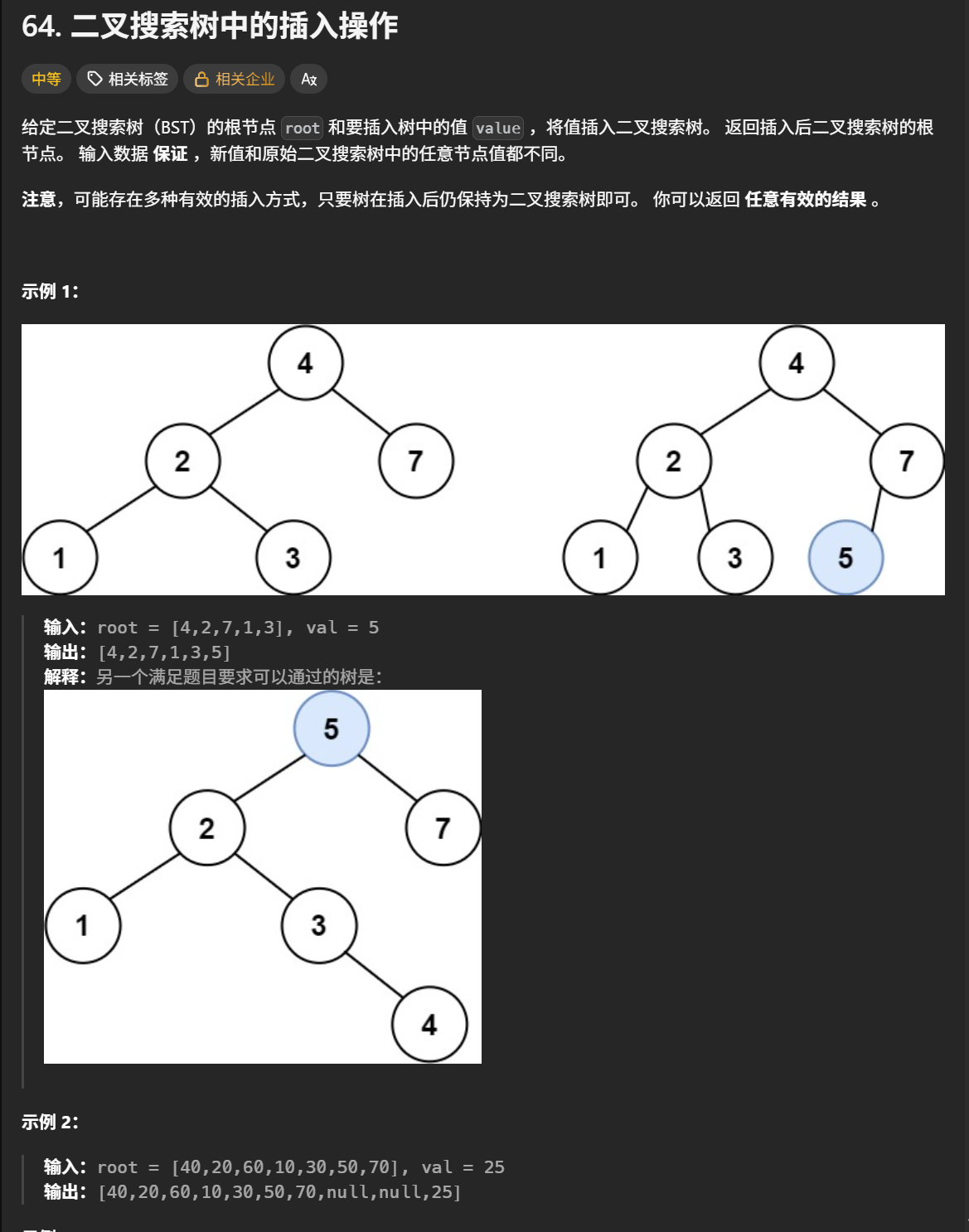
思路：二叉搜索树的插入操作无需重构二叉树，只要遍历二叉搜索树，找到空节点插入元素就可以了(创建子树)。

方法一：递归。

1.确定递归函数的参数和返回值：

（1）参数：根节点和要插入的元素。

（2）返回值：返回值类型为TreeNode，返回值用于实现新加入的节点与其父节点的赋值操作。

java 复制代码

public TreeNode insertIntoBST(TreeNode root, int val)

2.确定终止条件：当找到遍历的节点为null的时候，就找到了要插入节点的位置，把插入的节点返回给上一层（完成父子节点的赋值操作）。

java 复制代码

            if (root == null) // 如果当前节点为空，也就意味着val找到了合适的位置，此时创建节点直接返回。
            return new TreeNode(val);

3.确定单层递归的逻辑：因为本题的树是二叉搜索树，所以可利用其有序性质，而无需遍历整棵树，根据插入元素的数值大小与根节点数值大小的关系，决定递归方向（下一层已经将加入节点返回，这一层用root.left或root.right将其接住）。

java 复制代码

        if (root.val < val){
            root.right = insertIntoBST(root.right, val); // 递归创建右子树
        }else if (root.val > val){
            root.left = insertIntoBST(root.left, val); // 递归创建左子树
        }
        return root;

附代码：

java 复制代码

    class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if (root == null) // 如果当前节点为空，也就意味着val找到了合适的位置，此时创建节点直接返回。
            return new TreeNode(val);
            
        if (root.val < val){
            root.right = insertIntoBST(root.right, val); // 递归创建右子树
        }else if (root.val > val){
            root.left = insertIntoBST(root.left, val); // 递归创建左子树
        }
        return root;
    }
}

方法二：迭代。

思路：在迭代法遍历的过程中，需要记录当前遍历节点的父节点，这样才能做插入节点的操作。

java 复制代码

    class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if (root == null) return new TreeNode(val);
        TreeNode newRoot = root;
        //需要记录上一个节点，否则无法赋值新节点
        TreeNode pre = root;
        while (root != null) {
            pre = root;
            if (root.val > val) {
                root = root.left;
            } else if (root.val < val) {
                root = root.right;
            } 
        }
        //用父节点进行赋值
        if (pre.val > val) {
            pre.left = new TreeNode(val);
        } else {
            pre.right = new TreeNode(val);
        }

        return newRoot;
    }
}