目录
摘要
今天的学习让我对机器学习中的偏差和方差有了更清晰的认识。通过分析不同多项式阶数d对模型性能的影响,我理解了高偏差对应训练误差和验证误差都较高,而高方差则表现为验证误差远大于训练误差。正则化参数λ的选择同样关键:λ过大会导致欠拟合,λ过小则容易过拟合。交叉验证集帮助我们找到合适的λ值,从而平衡模型的复杂度和泛化能力。最后,我还学习了如何通过对比人类表现或基准算法来判断模型是否需要改进,这为实际应用中诊断模型问题提供了系统方法。
Abstract
Today's study delved into bias and variance diagnostics in machine learning. I learned to identify high bias (underfitting) and high variance (overfitting) by examining training error and cross-validation error. The choice of polynomial degree d and regularization parameter λ significantly impacts model performance---extreme values of either lead to poor generalization. Using cross-validation to select λ helps strike a balance. Additionally, establishing a performance baseline (e.g., human-level accuracy) provides context for evaluating whether errors stem from bias or variance, guiding further improvements.
一、偏差诊断和方差
开发机器学习系统的典型工作是我们有一个想法,我们几乎总会发现它的效果没你期待的那么号,所以构建机器学习系统的关键是如何决策接下来做什么,以提高其性能。
让我们回顾一下第一次上课举的例子
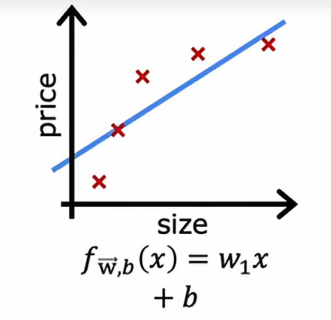
给定这个数据集,如果我们用一条直线拟合它,效果并不好,我们说这个算法有高偏差,或者它对这个数据集欠拟合,如果我们用四阶多项式拟合
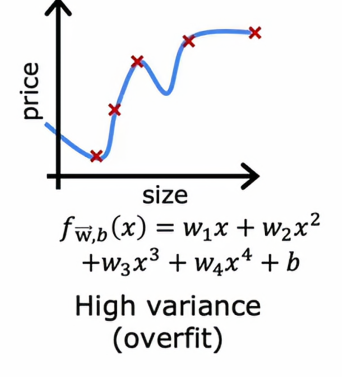
那么它有高方差,或者说它过拟合
如果我们用二次多项式拟合
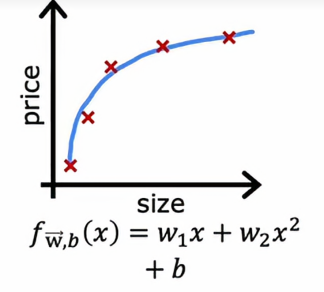
效果看起来相当不错,我们说这样刚刚好,因为这是一个只有单个特征x的问题,我们可以绘制函数f并像这样查看它,但如果我们有更多特征,我们无法绘制f并轻松可视化它是否表现良好,所以与其试图查看这样的图,更系统的方法来诊断或找出你的算法是高偏差还是高方差是查看我们的算法在训练集和交叉验证集上的表现
以上面欠拟合的情况为例,如果我们计算jtrain,算法在训练集上的表现如何呢,答案是表现并不好,所以我会说Jtrain在这里会很高,因为示例和实际之间存在相当大的错误,因此如果我们有一些新的例子Jcv,这些是算法以前没见过的样子,表现同样不好,所以Jcv也会很高,所以可以看出,高偏差的模型具有一个普遍的特征就是它在训练集上的表现不好
让我们再看向过拟合的情况为例,如果我们计算Jtrain,Jtrain会很低,说明它在训练集上表现的相当不错,非常适合训练数据,但是如果我们在训练集中没有出现过的其他例子上评估这个模型,那么我们会发现Jcv会很高,因此高方差的典型特征就是Jcv很高,高于Jtrain,换句话说,它在见过的数据上表现得比在没见过得数据上好得多
所以我们所作得重点就是通过计算Jtrain和Jcv看看Jtrain是否高或Jcv是否远高于Jtrain,这给了我们一种灵感,即使我们无法绘制出函数f,也能判断出我们的算法是高偏差还是高方差
最后我们再来看下最后一个情况,我们发现,在这种情况下,Jtrain和Jcv都很低,这说明它不仅在训练集上的表现良好、它在交叉训练集上的表现也很好,这说明该模型不仅能够很好的拟合现有的数据,也能很好地拟合之后从未出现过的数据
1、d值与Jcv和Jtrain的关系
我们再画一张图,其中图的横轴是我们拟合到数据的多项式的阶数,左边对应的是较小的d值,右边对应的是较大的d值,所以如果我们要绘制Jtrain作为多项式阶数函数的图像
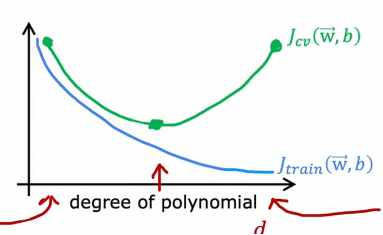
我们会发现随着我们拟合更高阶的多项式(这里我们假设没有用到正则化参数),因为当我们有一个非常简单的线性函数,即d值很小的函数,它总是与训练数据的拟合效果不是很好,当我们拟合一个三阶或四阶函数,它在训练集上的拟合程度会慢慢变好,所以一开始Jtrain很高,随着d增大,Jtrain的值慢慢变小
Jcv代表的是交叉训练集的误差,依据上面我们分析的三张图,我们发现,在d很小的时候,Jcv很大,说明算法不能很好低拟合之前没见过的新数据,但是当d很大的时候,Jcv也很大,解释的原因是因为这个算法过于拟合现有的数据,导致我们不能很好地推广到新数据当中,而直到d不大也不小的时候,Jcv才达到最小值,这也就是为什么,我们例子当中的二次多项式有着最小的Jcv和较小的Jtrain,这样的性能才是最好的
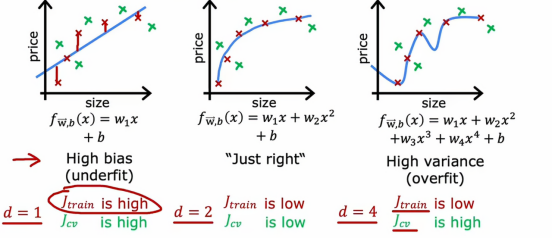
总结一下,如何诊断学习算法中的偏差和方差,如果我们的学习算法有高偏差或欠拟合数据,关键指标是Jtrain很高,这对应曲线的最左边,且通常Jtrain和Jcv很接近,高方差的关键指标是Jcv远大于Jtrain,即曲线最右边,实际上,还可能出现高偏差和高方差同时出现的情况,它的表现是Jtrain会很高并且Jcv会远大于Jtrain
二、正则化与偏差和方差
在上一个小节中,我们看到不同的多项式d如何影响模型的偏差和方差,在本节中,让我们看看正则化如何影响,特别是正则化参数λ的选择如何偏差和方差,因此影响整个算法的性能
在这个例子中,我们将使用一个四阶多项式,但我们会使用正则化来拟合这个模型
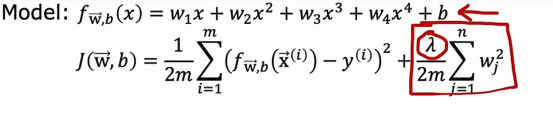
但这里的λ是控制我们在保持参数w小与拟合训练数据好之间权衡的正则化参数
让我们从将λ设置一个非常大的值开始
1、当λ很大时
如果我们设置λ = 10000时,我们会得到一个这样的图
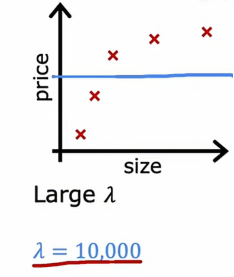
因为如果λ非常非常大,那么算法会非常倾向于保持这些参数w非常小,这样的话,w1、w2、w3、w4都几乎为0,所以该函数就近似于常数b,这就是为什么是图片上表现的常函数,这个模型很明显有很高的偏差,并且对数据欠拟合
2、当λ很小时
如果我们设置λ = 0,我们会得到一个这样的图
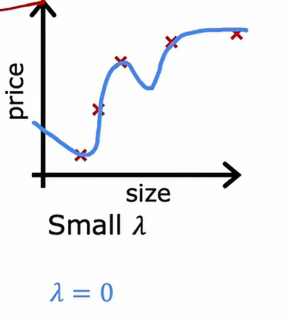
其实就相当于没有正则化参数,跟之前的图没有任何区别,它表现出的时高方差和过拟合
3、合适的λ值
如果我们选择了一个较为合适λ值(合适的λ值是根据具体情况去界定的),那么图看起来是这样的
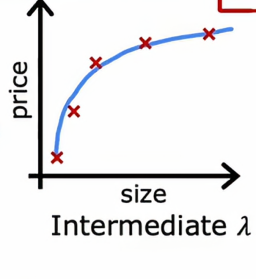
这样既能很好地拟合数据同时Jtrain和Jcv都很小
所以如果我们在决定使用什么样的λ作为正则化参数,交叉验证提供了一种方式,让我们看看怎么做,需要提醒的是,我们现在正在解决的问题是,如果我们在拟合一个四次多项式,并且我们正在使用正则化,这将类似与我们使用交叉验证选择多项式阶数d的程序

假设我们尝试使用λ等于0来拟合模型,我们会通过该λ来最小化成本函数,并得到一些参数w1、b1,然后计算Jcv,随着我们尝试的λ越多,我们得到Jcv就越来越多,使用这些不同的正则化参数拟合参数,然后评估它们在交叉验证集上的表现,我们可以尝试选择出最好的正则化参数,然后我们纵览全部Jcv,我们发现w5、b5的Jcv最小,那么我们会选择这个λ值,最后,如果我们想要报告一个泛化误差的估计值,我们会报告测试集误差,我们可以计算w5、b5的Jtest
为了进一步理解这个算法在做什么,让我们看看训练误差和交叉验证误差如何随着参数λ变化而变化,所以在下面图中,我们再次更改了x轴,这里的x轴代表的是正则化参数λ的值,上面我们说到,当λ很小的时候,会出现过拟合和高方差的情况,即Jtrain很小、但Jcv会很大,当λ很大的时候,会出现欠拟合和高偏差的情况,即Jtrain很大,Jcv也很大。
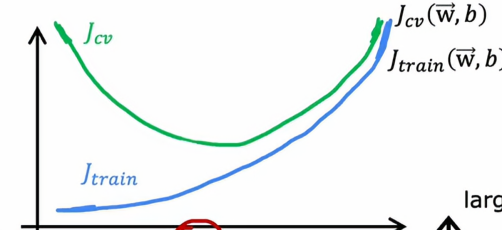
三、建立表现基准
让我们看一些具体的例子,来判断Jtrain和Jcv如何判断一个学习算法,这次让我们把目光放到语音识别上

我们让用户有时候可以用语音输入,这样我们得到训练失误的概率是10.8%,这说明机器有10.8%概率判断失败,并且我们还要测量语音识别算法在单独的交叉验证集上的表现,假设它的错误率是14.8%,乍一看感觉机器的出错的概率好像还很高,但是实际上人类出错的概率为10.6%,我们发现人和机器的差别好像很小,在现实生活中,如果训练误差和人类现有水平差别不大的话,就说明机器在方面表现还是出色的,但是这里我们发现一个问题,就是Jcv和Jtrain的差距很大,按照我们上一节的知识来判断,这应该属于的时方差问题而不是偏差问题
所以判断训练误差是否偏高时,通常建立一个基线水平的表现是有用的,通俗来说,就是我们合理期望我们的学习算法最终达到的错误水平是多少,一种常见的办法就是测量人类在这项任务上表现有多好,因为人类非常擅长理解语音数据,另一种估算基线方法看看是否有一些竞争算法,可能是别人实现过的早期版本或者现有版本。
当我们评估一个算法是否有高偏差或高方差时,我们可以查看基线水平的表现,测量的两个关键量是训练误差与基线水平之间的差异,然后我们还要看训练误差和交叉验证误差之间的差距。
总结
今天的学习让我掌握了诊断机器学习模型偏差和方差的方法。通过绘制不同d值对应的训练误差和验证误差曲线,我直观地看到了欠拟合和过拟合的表现特征。正则化参数λ的调节过程也让我意识到平衡拟合程度的重要性------λ太大模型会过于简单,λ太小又容易过度复杂。交叉验证集在模型选择中起到了关键作用,帮助我避免了对测试集的误用。最后,引入人类表现作为基准让我明白了如何客观评估模型性能,判断改进方向。这些知识让我对优化模型有了更清晰的思路,尤其是在实际项目中如何系统性地解决欠拟合或过拟合问题。