机器学习-KNN算法实战及模型评估可视化(C++/Python实现)

目录

一、前言

实现环境

二、KNN算法讲解

[2.1 算法原理](#2.1 算法原理)

[2.2 算法优缺点](#2.2 算法优缺点)

[2.2.1 优点](#2.2.1 优点)

[2.2.2 缺点](#2.2.2 缺点)

三、评估标准介绍

[3.1 ROC曲线](#3.1 ROC曲线)

[3.1.1 基本原理](#3.1.1 基本原理)

[3.1.2 计算公式](#3.1.2 计算公式)

[3.2 AUC](#3.2 AUC)

四、实战例题分析

[4.1 问题导入](#4.1 问题导入)

[4.1.1 问题](#4.1.1 问题)

[4.1.2 数据集类型](#4.1.2 数据集类型)

[4.2 问题分析](#4.2 问题分析)

[4.3 实现流程](#4.3 实现流程)

[4.3.1 流程示意图](#4.3.1 流程示意图)

[4.3.2 实现步骤讲解](#4.3.2 实现步骤讲解)

[4.3.2.1 导入数据](#4.3.2.1 导入数据)

[4.3.2.2 预处理](#4.3.2.2 预处理)

[4.3.2.3 最佳K值的选择](#4.3.2.3 最佳K值的选择)

[4.3.2.4 计算FPR和TPR、AUC并可视化ROC曲线](#4.3.2.4 计算FPR和TPR、AUC并可视化ROC曲线)

[4.3.2.5 计算特征混淆矩阵并可视化热力图（可选）](#4.3.2.5 计算特征混淆矩阵并可视化热力图（可选）)

五、C++实现

[5.1 环境准备](#5.1 环境准备)

[5.1.1 环境选择和参考文献](#5.1.1 环境选择和参考文献)

[5.1.1.1 gnuplot下载](#5.1.1.1 gnuplot下载)

[5.1.1.2 matplot++下载](#5.1.1.2 matplot++下载)

[5.1.1.3 参考文献](#5.1.1.3 参考文献)

[5.1.2 VS2022环境搭建](#5.1.2 VS2022环境搭建)

[5.1.2.1 文件管理](#5.1.2.1 文件管理)

[5.1.2.2 配置调整](#5.1.2.2 配置调整)

[5.1.2.3 premake配置（可以代替5.1.2.2）](#5.1.2.3 premake配置（可以代替5.1.2.2）)

[5.2 代码实现](#5.2 代码实现)

[5.2.1 使用的头文件](#5.2.1 使用的头文件)

[5.2.2 使用结构体](#5.2.2 使用结构体)

[5.2.3 导入数据](#5.2.3 导入数据)

[5.2.4 预处理](#5.2.4 预处理)

[5.2.4.1 归一化](#5.2.4.1 归一化)

[5.2.4.2 洗牌](#5.2.4.2 洗牌)

[5.2.5 选择最佳k值](#5.2.5 选择最佳k值)

[5.2.5.1 计算欧几里得距离](#5.2.5.1 计算欧几里得距离)

[5.2.5.2 获取邻居各类别的数量](#5.2.5.2 获取邻居各类别的数量)

[5.2.5.3 选择出现最多的类别作为预测结果](#5.2.5.3 选择出现最多的类别作为预测结果)

[5.2.5.4 使用k折交叉验证计算准确率和三分类混淆矩阵](#5.2.5.4 使用k折交叉验证计算准确率和三分类混淆矩阵)

[5.2.5.5 网格搜索](#5.2.5.5 网格搜索)

[5.2.6 计算FPR和TPR](#5.2.6 计算FPR和TPR)

[5.2.6.1 将多类型数量转换为概率](#5.2.6.1 将多类型数量转换为概率)

[5.2.6.2 计算某一类型作为正例时单个点的FPR和TPR](#5.2.6.2 计算某一类型作为正例时单个点的FPR和TPR)

[5.2.6.3 将某一类别所有点数据整理补全起来](#5.2.6.3 将某一类别所有点数据整理补全起来)

[5.2.7 计算AUC](#5.2.7 计算AUC)

[5.2.8 可视化](#5.2.8 可视化)

[5.2.9 mian函数调用](#5.2.9 mian函数调用)

[5.3 运行结果展示](#5.3 运行结果展示)

六、Python实现

[6.1 环境准备](#6.1 环境准备)

[6.1.1 在虚拟环境中配置环境](#6.1.1 在虚拟环境中配置环境)

[6.1.2 配置Pycharm](#6.1.2 配置Pycharm)

[6.2 代码实现](#6.2 代码实现)

[6.3 运行效果展示](#6.3 运行效果展示)

七、总结

---

一、前言

本系列诞生的原因是小编被学校老师布置了作业，但既然要写成博客，那就不能敷衍了事，小编花了很多时间研究如何让KNN算法的时间、空间开销降低下来，努力了快一周了，还是没有成效，不过实战的代码实现都被打磨过，还是勉强能用的。

实现环境

C++：集成开发环境------VS2022，可视化库------matplot++

python：集成开发环境------Pycharm，数学库------numpy，可视化库------matplotlib

二、KNN算法讲解

2.1 算法原理

KNN，中文全称K近邻算法 ，是监督学习 的一种算法，通过计算待测样本与已知样本之间的距离 ，选择距离最近的k个 邻居，将出现最多的类别作为预测的类别。通常用于解决分类问题 ，也可以用作解决回归问题 ，将k个邻居的数值平均值作为预测结果。总之，就是通过预测点周围的点决定这个点的性质 ，数据集本身就是一个模型。实现起来比较简单，适合刚入门机器学习的读者。

但是这样讲还是太抽象了，下面直接结合着图片讲解。

假设图中蓝点圈起来的点都是某个k下的邻居，此时，我们不难看到，圈中红叉比黑叉多 ，此时蓝点选择红叉对应的类别作为预测蓝点类别的结果。

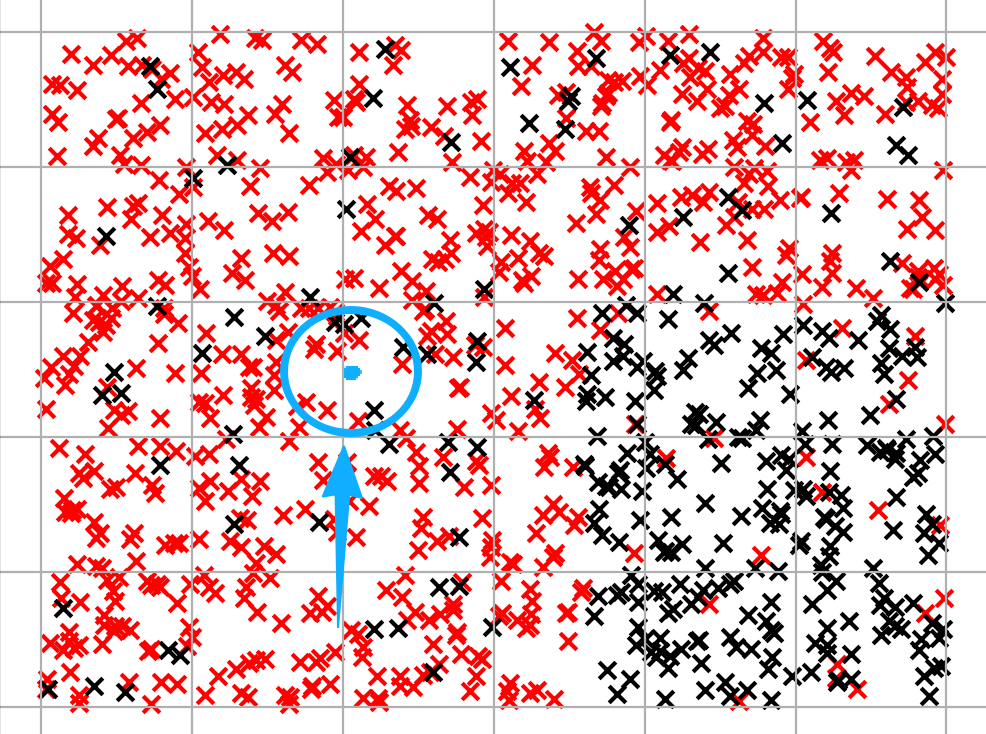
图2-1

2.2 算法优缺点

在利用机器学习解决事情时，算法的选择是必不可少的一个过程。只有选择了较为合适的算法去解决问题，才能更高效地处理问题。所以，下面介绍这个算法的优缺点，方便选择利用。

2.2.1 优点

1. 这个算法是懒惰的，相较于其他的机器学习算法，不用做什么复杂的训练，不用去使用什么高深的数学公式，实现简单，逻辑上更贴近人类直觉；
2. 不用像其他算法需要训练模型，耗时较小，容易得到结果；
3. 既能解决回归问题，也能解决分类问题，适用性强；
4. 当有新的样本进入数据集后，无需更新模型，因为数据集本身就是模型，可以直接用来预测。

2.2.2 缺点

1. 每次使用时，都需要将所有数据导入内存，内存开销大；
2. 预测时需要对预测点的k个邻居求距离，如果k设置的比较大，预测阶段可能会比较慢；
3. 对K的设置敏感（如下图，随着K的变化，准确率不停上下波动），需要使用合适的算法确定K这个超参（在模型外人工设置的参数）；
4. 在多个维度，对特征敏感，有的特征在上千的数量级波动，有的特征在几十、零点几的数量级波动，这时候直接计算距离会导致上千数量级的特征影响很大，需要进行预处理。

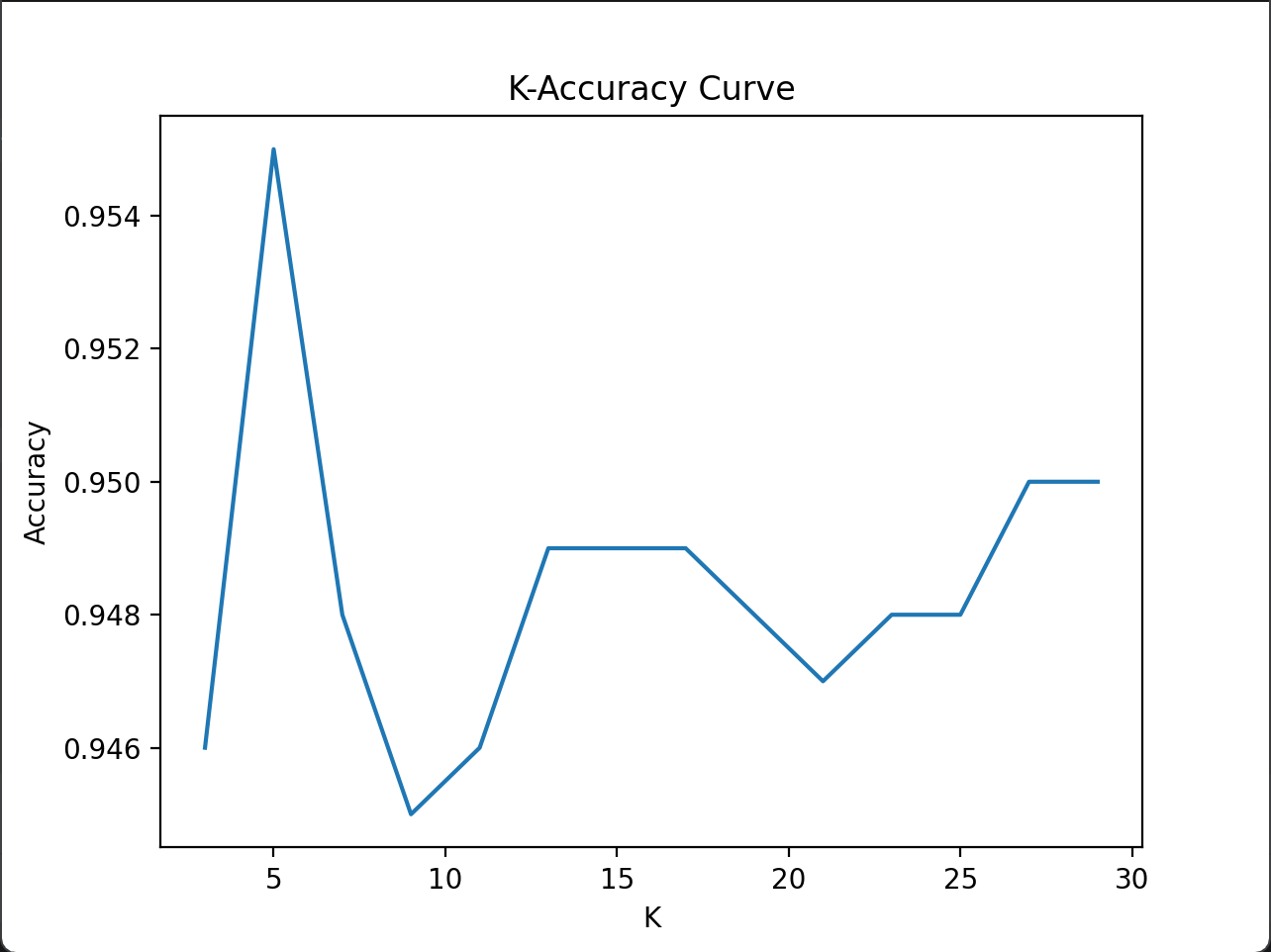
图2-2

三、评估标准介绍

本文使用的评估是ROC曲线及其对应的AUC值。

3.1 ROC曲线

ROC曲线，即受试者工作特征曲线，用于**衡量二分类模型的"区分能力"**的，就是说，ROC曲线适用于解决分类问题的模型的评估，本文的实战是个分类问题，可以使用这种评估标准评估。

3.1.1 基本原理

获取模型预估某个预测点的概率，通过连续的单向调整的置信度（从1到0或从0到1，单向是为了减少数据处理，可选 ），获得一连串FPR和TPR值。其中，FPR值是所有反例 中被错误当作正例 的比例，TPR值是所有正例 中正确识别出来 的正例 的比例，换句话说，当模型正确识别正例的能力越高、错误识别正例的能力越低 ，这个模型的分类能力就越强。

FPR和TPR的具体解释：

FPR (False Positive Rate)，即假正确率，是用来描述模型中反例被误识别为正例的比例，分母就是所有反例，比例越低 ，即越难误识别，模型分类能力越强。
TPR (True Positive Rate)，即真正确率，也叫召回率，是用来描述模型中正例被正确识别的比例，分母是所有正例，比例越高，即越容易区分出正例，模型分类能力越强。

3.1.2 计算公式

那么FPR和TPR怎么计算？

这里涉及到四个数据：TP(真正例)、FP(假正例)、FN(假反例)、TN(真反例)

这里的真假 ，是判断预测结果是否符合实际 ，预测为正例而实际为反例，就是假；

后面的正反 ，是预测的结果

|------|---------|---------|
| | 实际正例 | 实际反例 |
| 预测正例 | TP(真正例) | FP(假正例) |
| 预测反例 | FN(假反例) | TN(真反例) |

FPR计算公式：

TPR计算公式：

然而，当出现图3-1的情况时，两条曲线很接近，我们没办法通过肉眼判断那个模型分类效果好，这时候就要使用新的依据了。看图3-2，这时候，我们会怎么判断哪条曲线的模型分类能力更好呢？根据前面说的"正确识别正例的能力越高、错误识别正例的能力越低**"** ，我们可以很快地判断出橙色的曲线模型分类效果好。我们不难发现，曲线在越左上方，效果越好 ，这一点可以使用曲线下方围成的面积来描述。

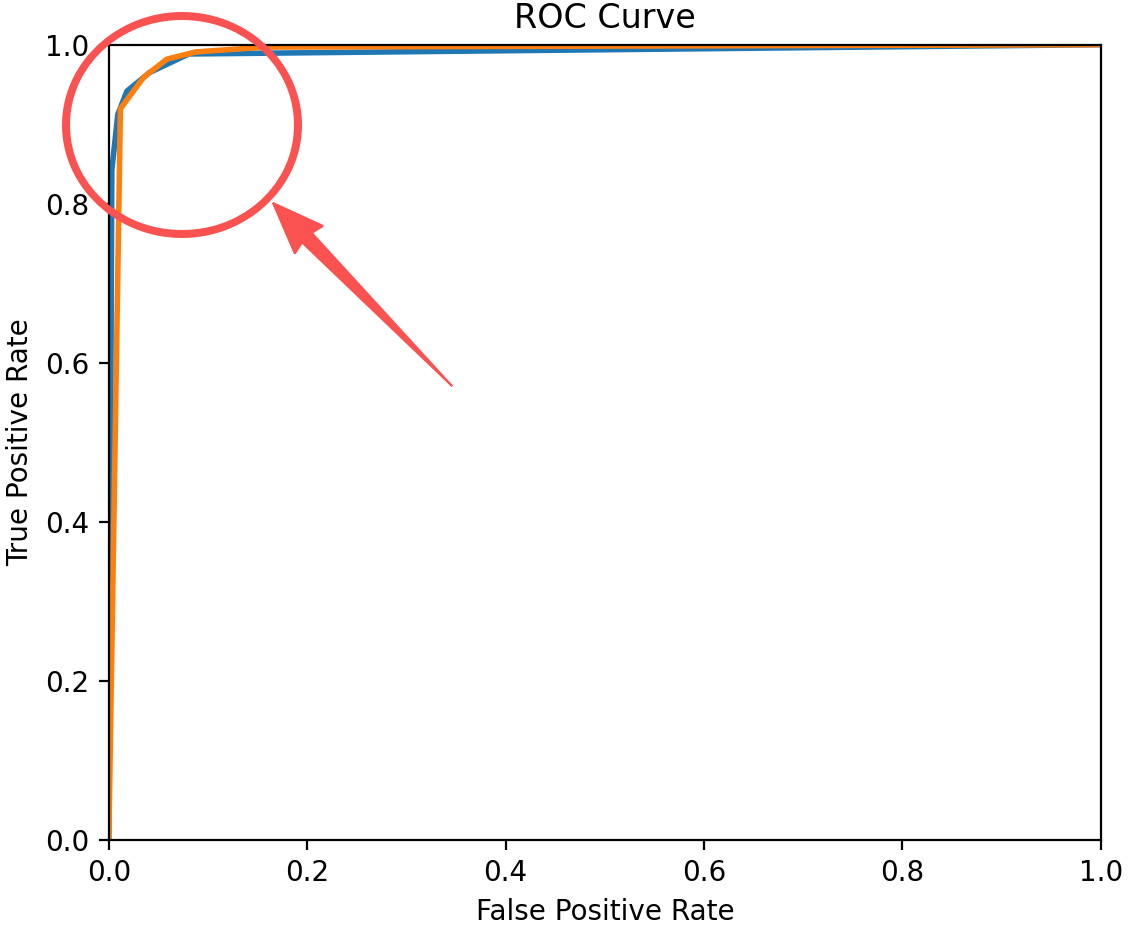
图3-1

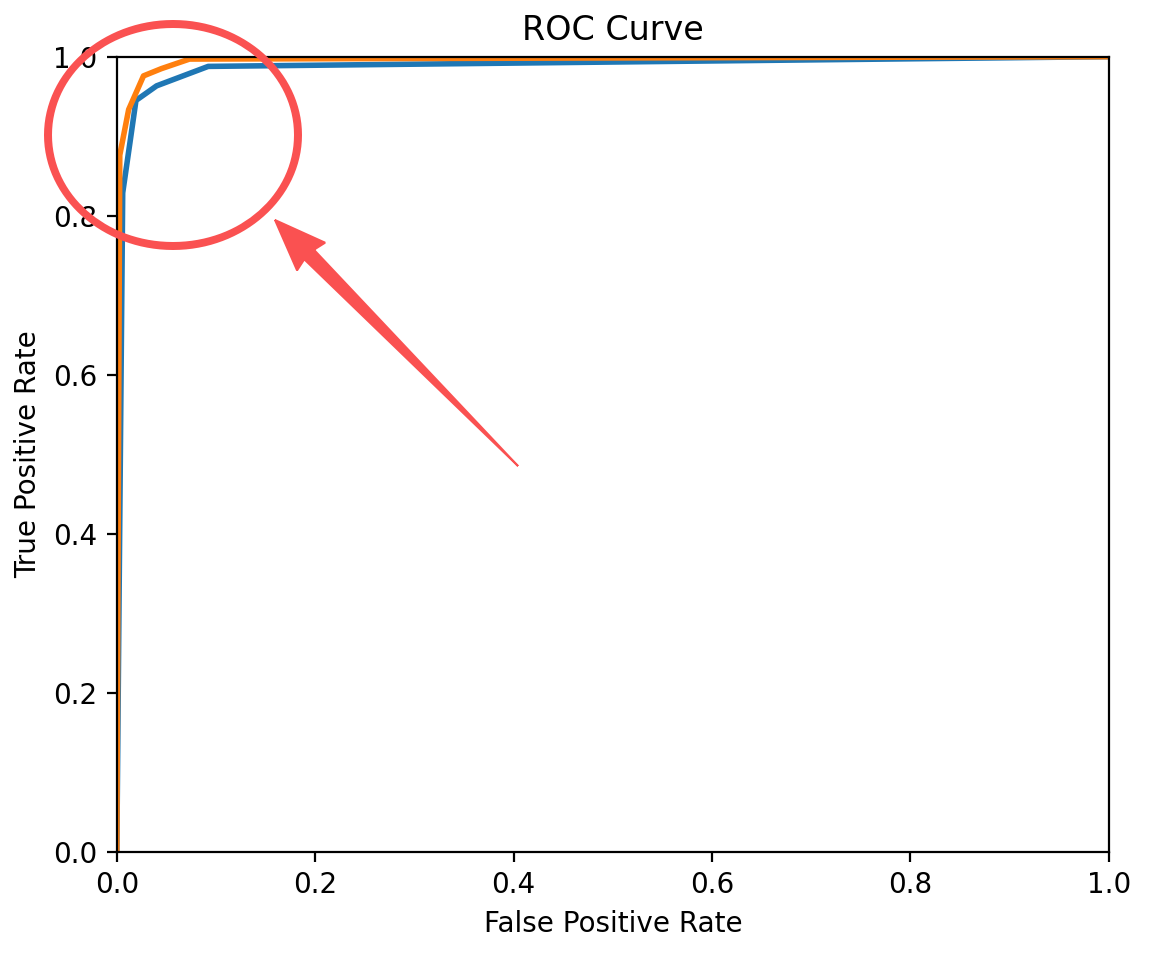
图3-2

3.2 AUC

AUC(Area Under ROC Curve)，ROC曲线下方的面积。正如上面所说的，为了对模型分类能力有更标准的衡量，我们引入了AUC的概念。曲线越接近左上方，AUC围的面积就越接近1，所以，我们希望AUC的数值能越靠近1越好。

本文的特殊计算方式

本文采用梯形法计算，将每个小段的auc累加起来，对应的公式：

四、实战例题分析

4.1 问题导入

4.1.1 问题

海伦一直使用在线约会网站寻找适合自己的约会对象。她曾交往过三种类型的人：

• 不喜欢的人
• 一般喜欢的人
• 非常喜欢的人

这些人包含以下三种特征：

• 每年获得的飞行常客里程数
• 玩视频游戏所耗时间百分比
• 每周消费的冰淇淋公升数

该网站现在需要尽可能向海伦推荐她喜欢的人，需要我们设计一个分类器，根据用户的以上三种特征，识别出是否该向海伦推荐。

4.1.2 数据集类型

|---|--------------|--------------|--------------|------|
| | 每年获得的飞行常客里程数 | 玩视频游戏所耗时间百分比 | 每周消费的冰淇淋的公升数 | 样本分类 |
| 1 | 400 | 0.8 | 0.5 | 1 |
| 2 | 134000 | 12 | 0.9 | 3 |
| 3 | 20000 | 0 | 1.1 | 2 |
| 4 | 32000 | 67 | 0.1 | 2 |

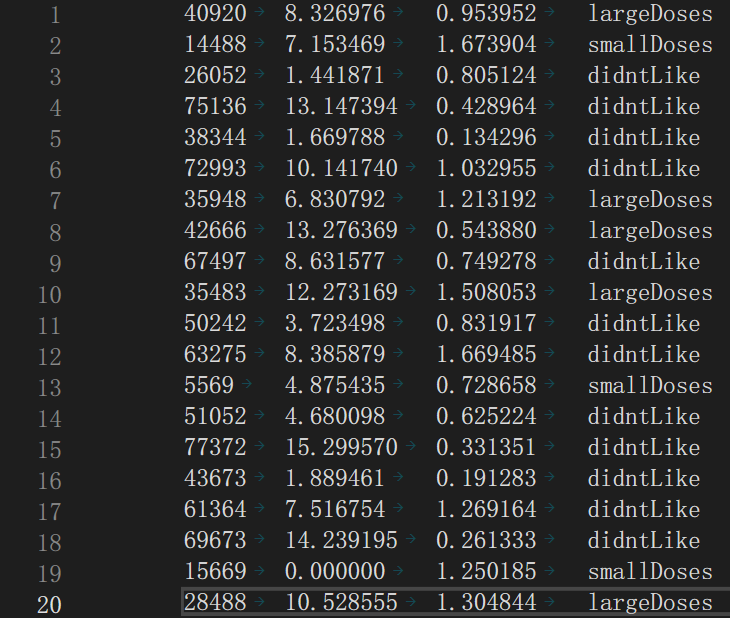
图4-1

4.2 问题分析

题目给出了三个特征维度，通过观察，我们可以发现，"每年获得的飞行常客里程数"这一特征维度的数据比另外两个大了2-3个数量级 ，我们还选择了欧几里得距离作为距离标准，所以需要对数据进行预处理 ，让每个特征维度的权重基本一致。

正如数据集类型表格给的样本分类，我们需要在导入图中数据时，将这些字符串转换为整型数据，方便使用。（largeDoses -- 0, smallDoses -- 1, didntLike -- 2，这里和表中不一样是为了方便后续处理）

4.3 实现流程

4.3.1 流程示意图

不是流程图，以为没有按流程图的标准画，"计算特征混淆矩阵"和"可视化热力图"可选

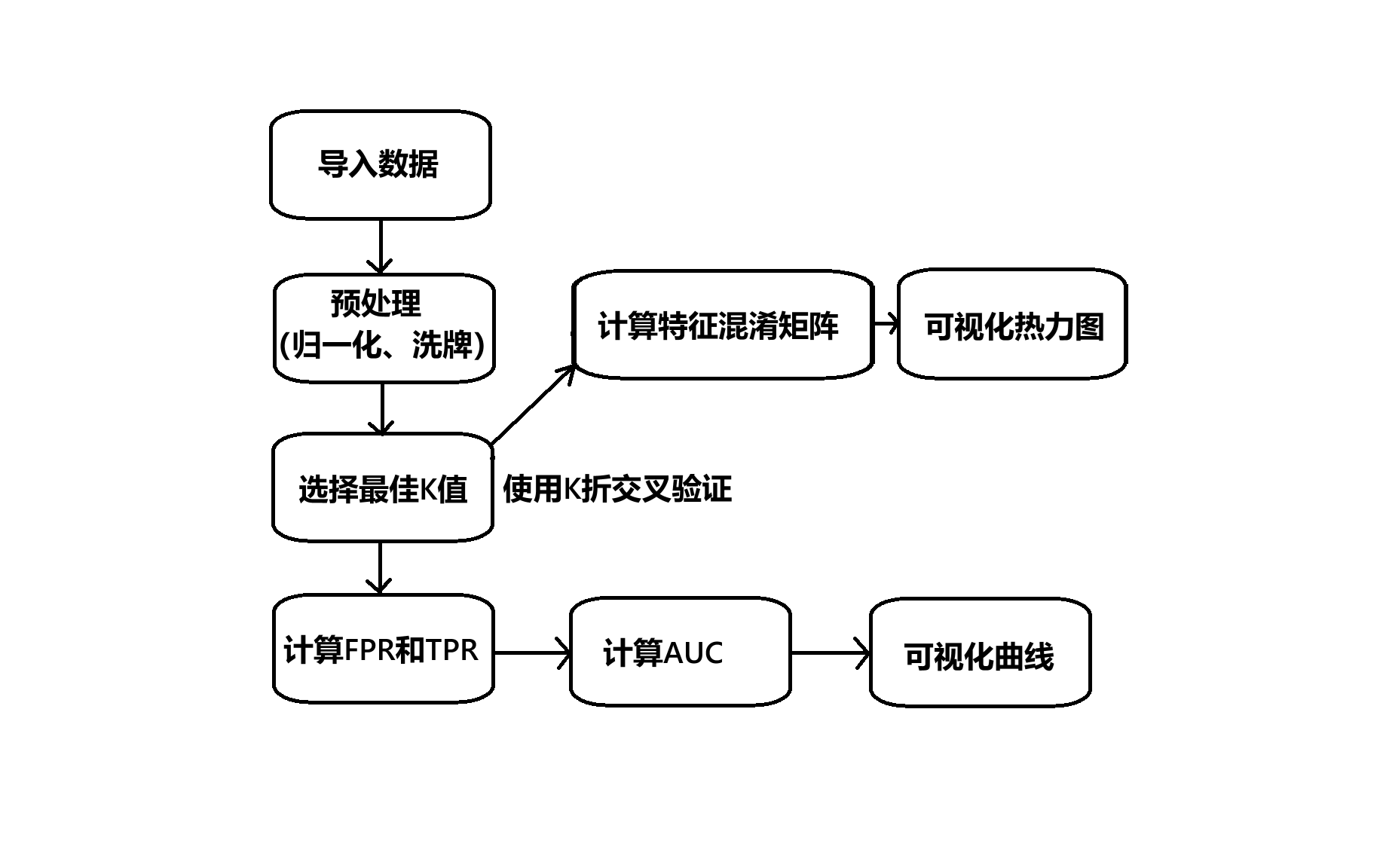
图4-2

4.3.2 实现步骤讲解

4.3.2.1 导入数据

这个是根据数据集的类型和维度数量等等决定的，前面也有具体分析了，这里就不赘述，可以看后面的代码实现部分。

4.3.2.2 预处理

归一化 ：将所有数据按原范围大小，均匀压缩到0-1的范围内，如25、50、75、125，原范围25-125，对应0-1范围0、0.25、0.50、1。给出公式：

洗牌 ：数据集的数据可能呈现出部分特征集中在某一特定位置，这就好比我们吃拌面时，厨师往往只负责将酱料撒在一个区域，我们需要搅拌面来让酱均匀地分布在每个地方，不然吃起来会一部分味道寡淡一部分很浓。对于数据集而言，遇到这种情况是会影响生成的模型的能力的，所以我们需要把原来的数据集打乱 ，让某些过于集中的特征分散开来，提高模型预测的准确性。

4.3.2.3 最佳K值的选择

正如前面2.2.2中说的，k的选取是很重要的，常见的选择方法有经验值法 （直接设置参数）和交叉验证法（网格搜索+交叉验证）。

网格搜索 ：实际上就是穷举所有可能的情况，比较每个情况的效果（在这里是准确率），十分简单暴力，但是时间、空间开销大。
交叉验证：假设有个交叉验证是m次n折交叉验证，将数据集分成n份，从1-n份，每次一小份作为测试集，其他作为验证集，计算准确率，重复m次。

在本文的实战中，还涉及到了距离的计算，常见的距离计算有两种：欧几里得距离 和曼哈顿距离

欧几里得距离计算公式（x和y是同一特征维度的，i表示不同的特征维度）：

曼哈顿距离计算公式（和上面的变量一个含义）：

距离公式的选择

从公式上看，我们可以发现欧几里得距离的计算成本比较高 ，需要平方 ，而曼哈顿距离计算只有加减法和绝对值 ，而且如果我们使用欧几里得距离作为计算标准，是必须要对数据进行归一化 的；但是我们的实战数据量只有一千个多个，计算成本的影响较小 ，且我们需要全局的评估，欧几里得距离的"全局相似性"表达更好，所以选择欧几里得距离

4.3.2.4 计算FPR和TPR、AUC并可视化ROC曲线

前面提到过，这里就不展开了。

4.3.2.5 计算特征混淆矩阵并可视化热力图（可选）

这一步主要是查看我们的分类器模型分类的结果，使用热力图直观地查看结果，方便我们优化程序。特征混淆矩阵，是基于特征预测的类别和实际类别进行分类。就像下面的这张表

|----------------|----------------|----------------|---------------|
| | largeDoses(实际) | smallDoses(实际) | didntLike(实际) |
| largeDoses(预测) | | | |
| smallDoses(预测) | | | |
| didntLike(预测) | | | |

五、C++实现

5.1 环境准备

我们只需要一个额外的第三方库，C++社区有很多可视化第三方库，这里我们选择matplot++

5.1.1 环境选择和参考文献

5.1.1.1 gnuplot下载

官方链接：我选择的是5.4.6版本的，和我版本不一样可能有些代码会报错

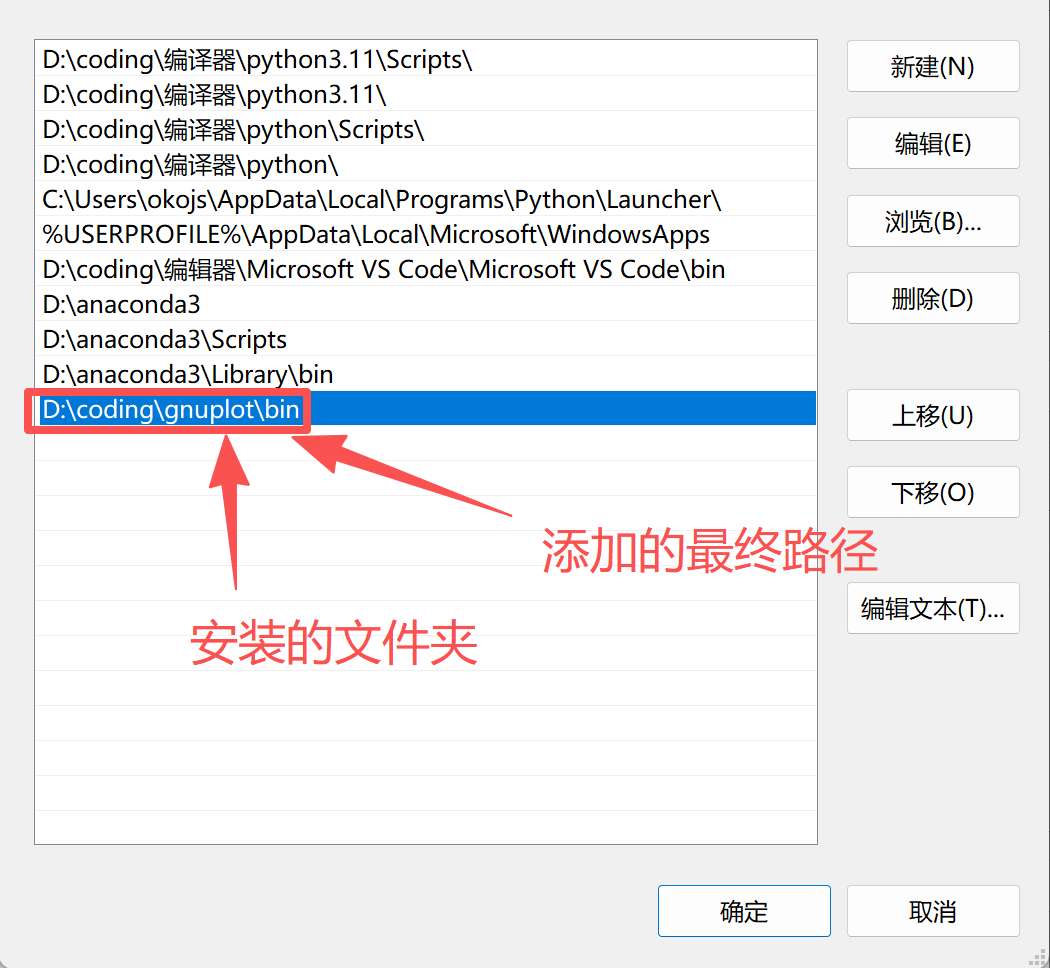
需要添加环境变量，上一篇文章有提到过，这里不赘述了，添加下图圈起来的那行就可以了，不要直接抄，除非你和我安的地方一样。添加这一行是为了能正常使用matplot++

验证：在终端输入gnuplot，出现下面的情况就添加成功了

gnuplot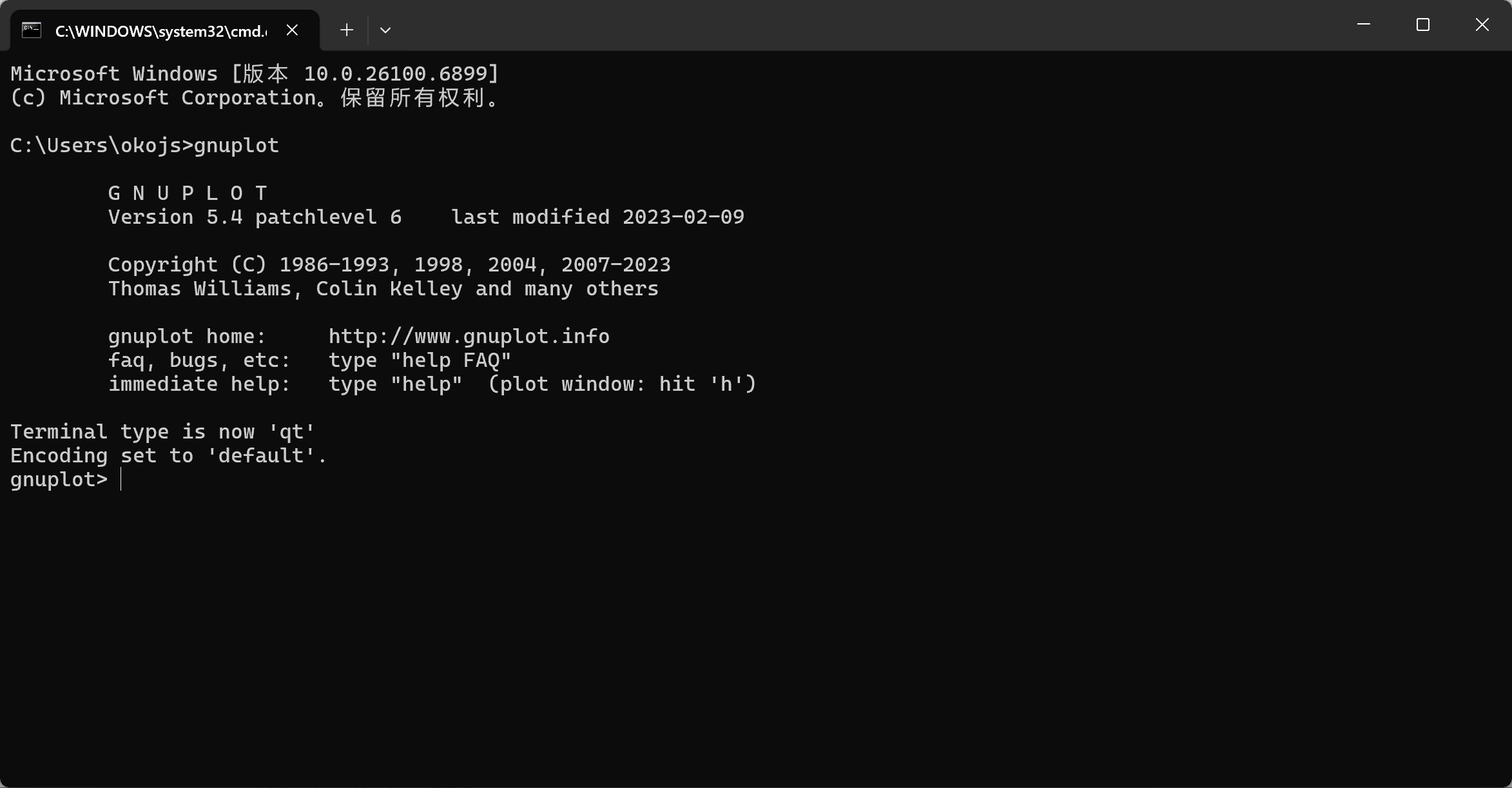

5.1.1.2 matplot++下载

官方链接：matplot++发行版，由于下面的两个参考文献是直接引用发行版的静态库的，所以我只能选择1.2.0版本的，gnup也降到发行这个版本之前的版本

5.1.1.3 参考文献

晓程序员介绍的安装教程
这位大佬的补充

5.1.2 VS2022环境搭建

5.1.2.1 文件管理

我把matplot++放到了我建立的解决方案的其中一个项目的目录下

E:\code\CML\KNN_Project1\KNN_Project1\vendor\Matplot++ 1.2.0

5.1.2.2 配置调整

下面直接放我的配置，tips：一定要把配置改成release，不然会报错

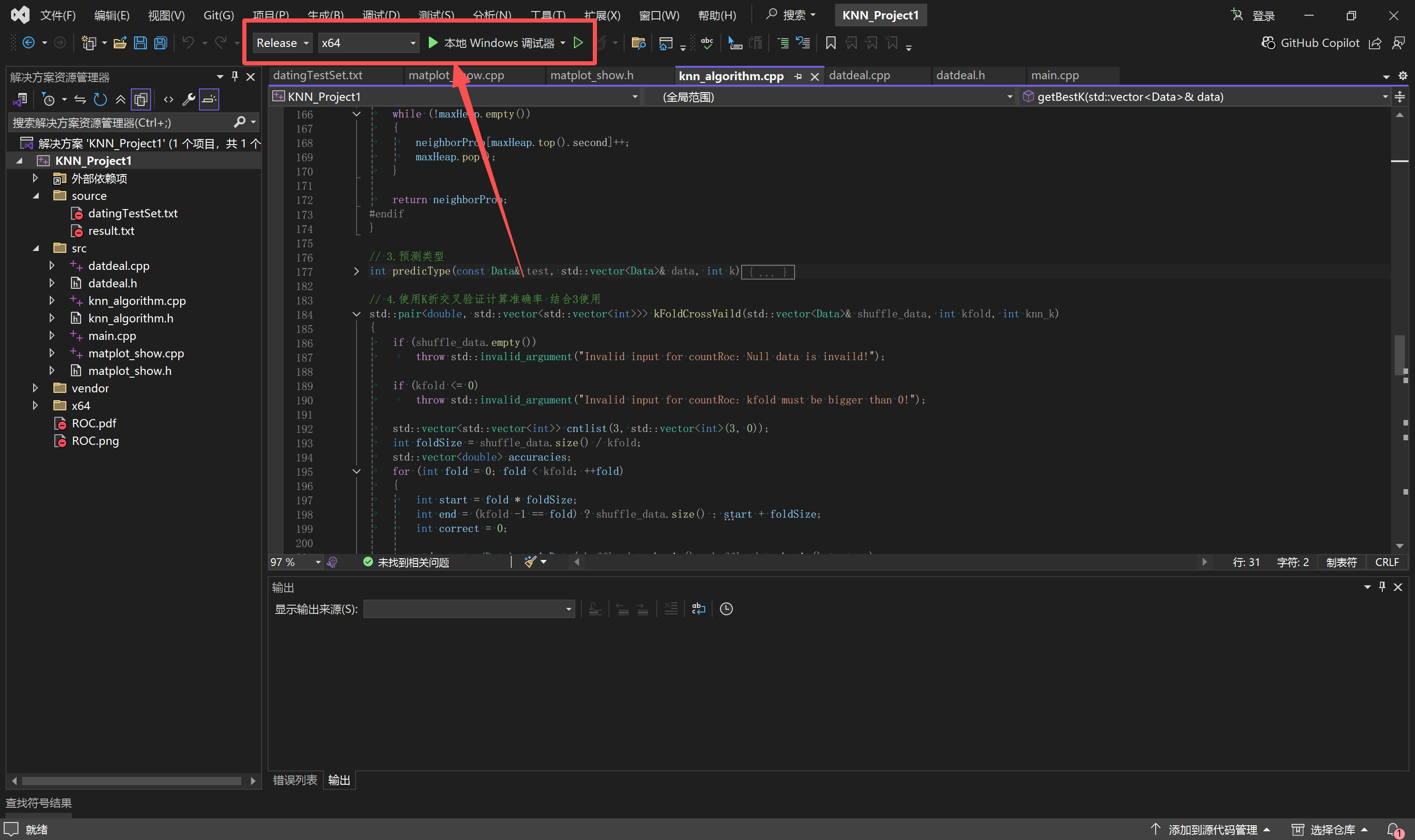
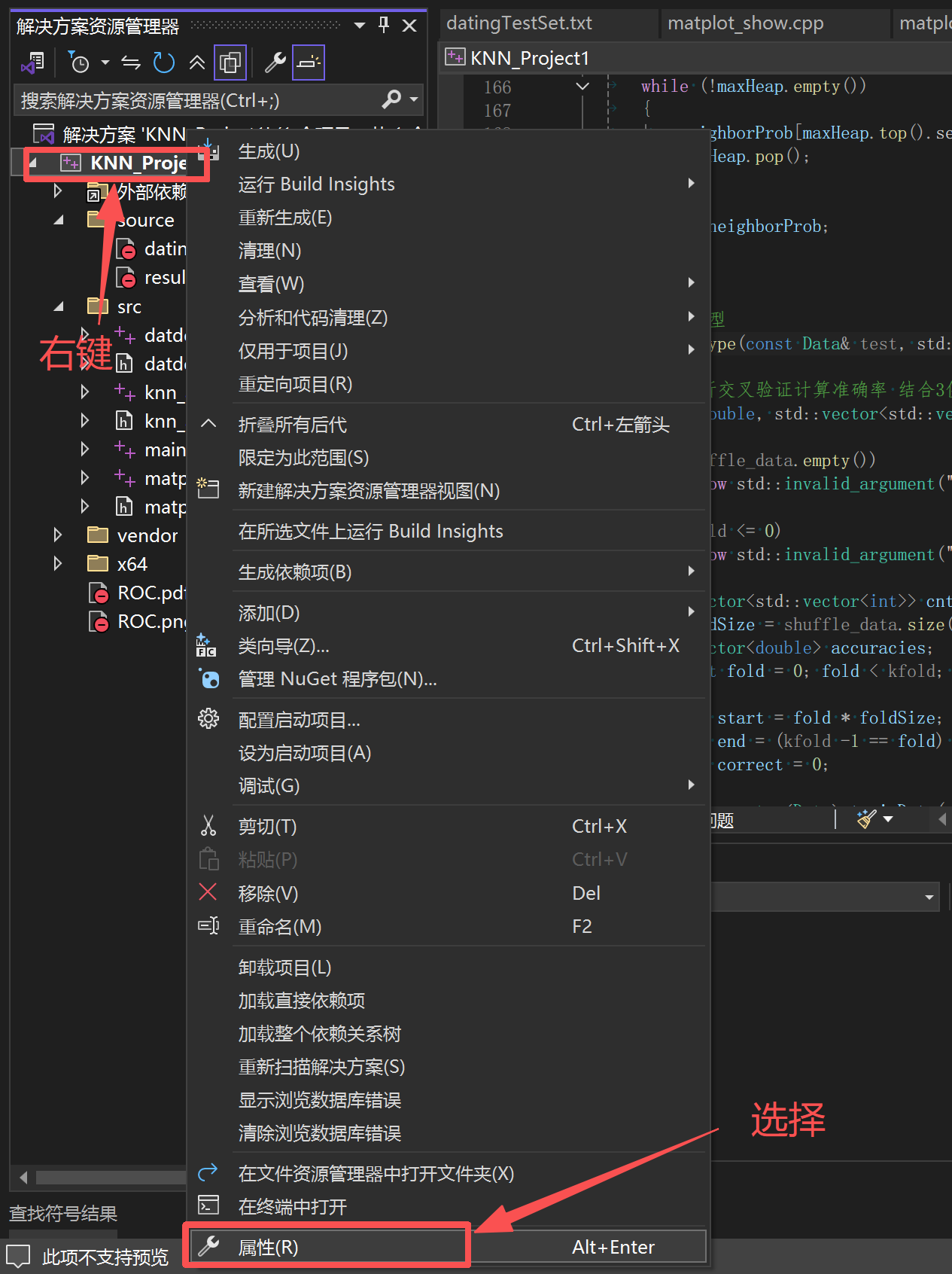
右键项目，选择"属性"

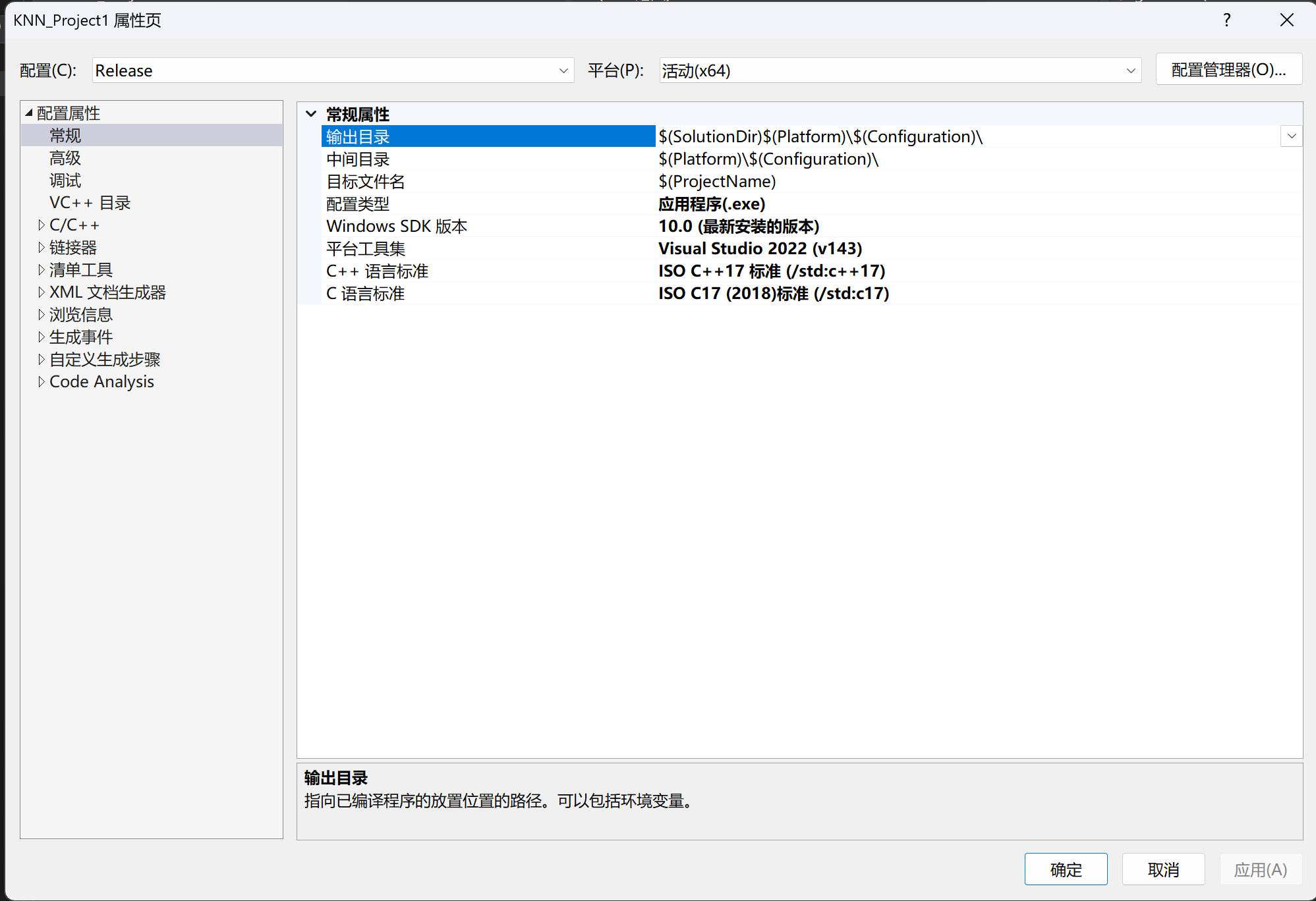
接下来一系列的配置图片，路径是跟着解决方案的，只要把本文上的项目修改你自己命名的项目名即可使用

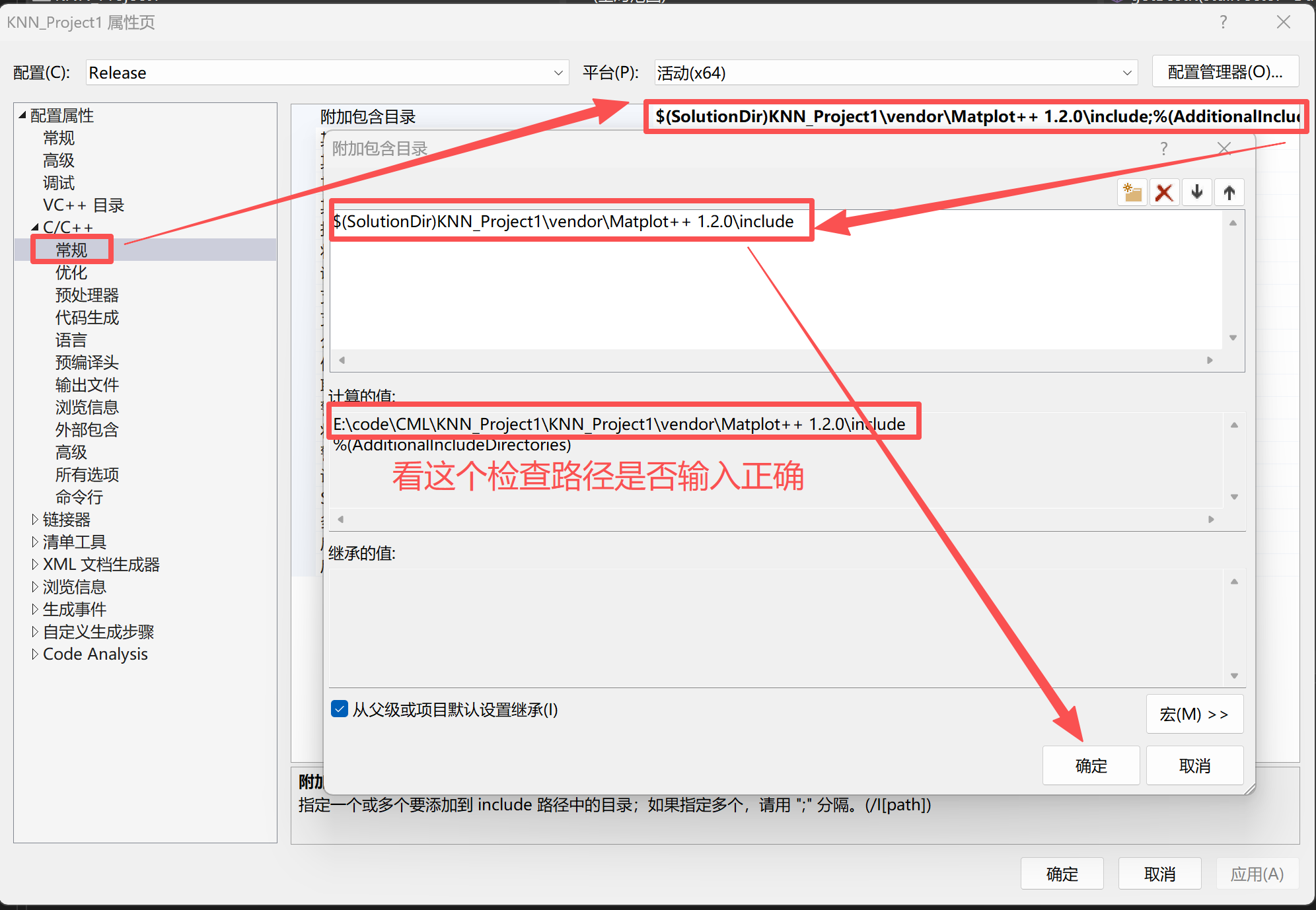
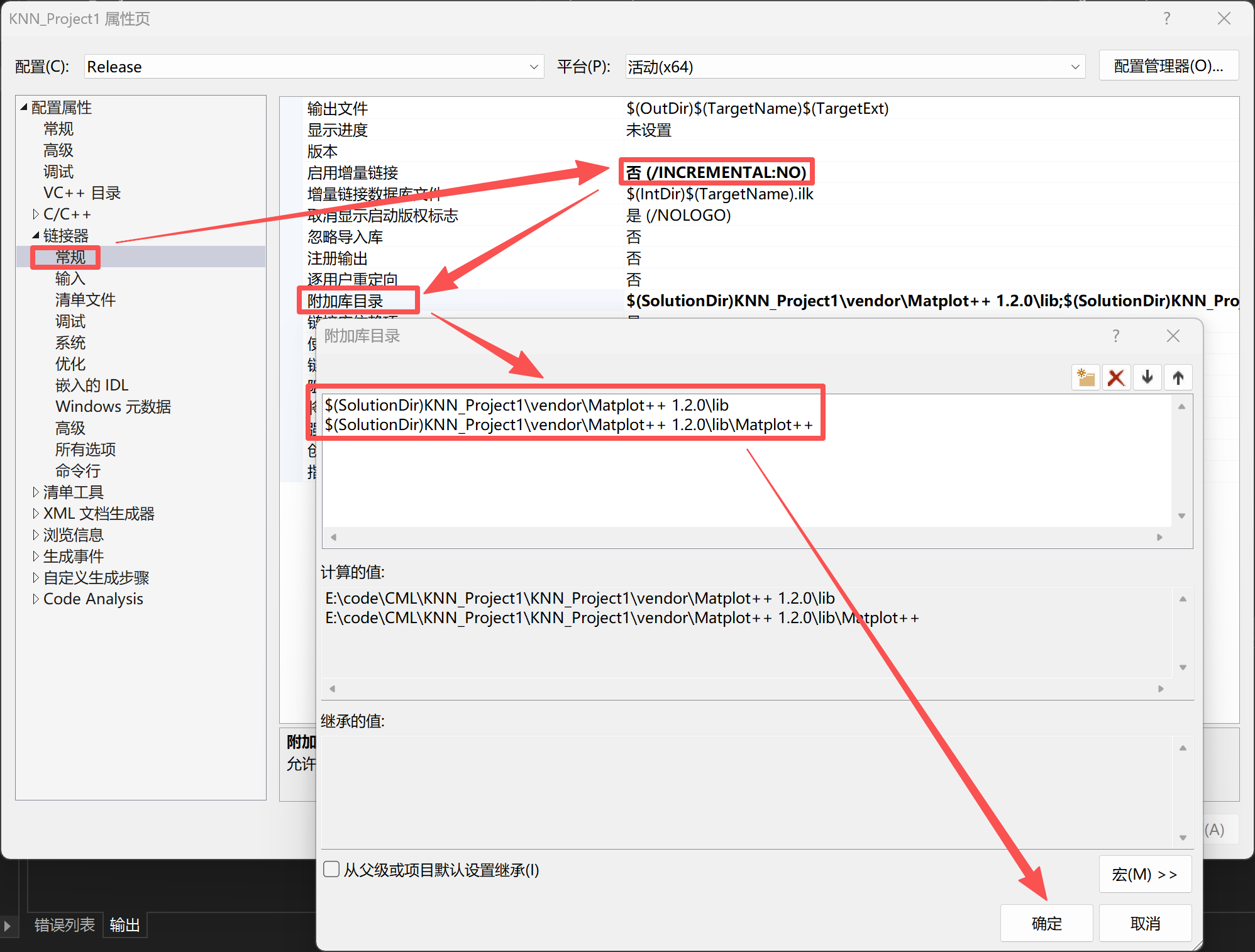
附加包含目录有个选框，选择"编辑"就得到最上层的这个窗口，记得点击确认保存，下面出现这样的图片同理

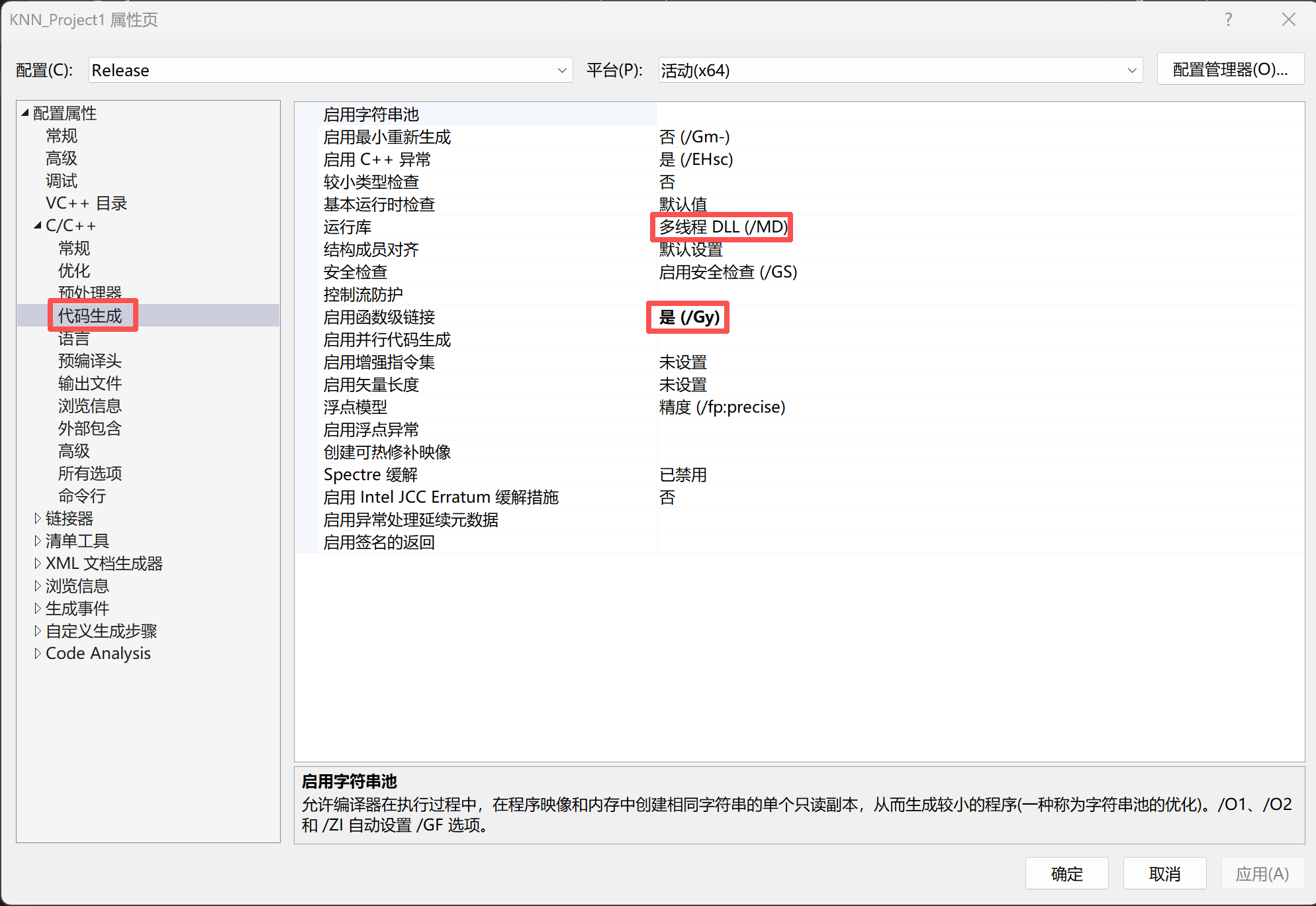
matplot++的两个静态库，可根据实际位置调整，一般都是一个在lib里，一个在lib\Matplot++里。在链接器中链接：

nodesoup.lib

matplot.lib

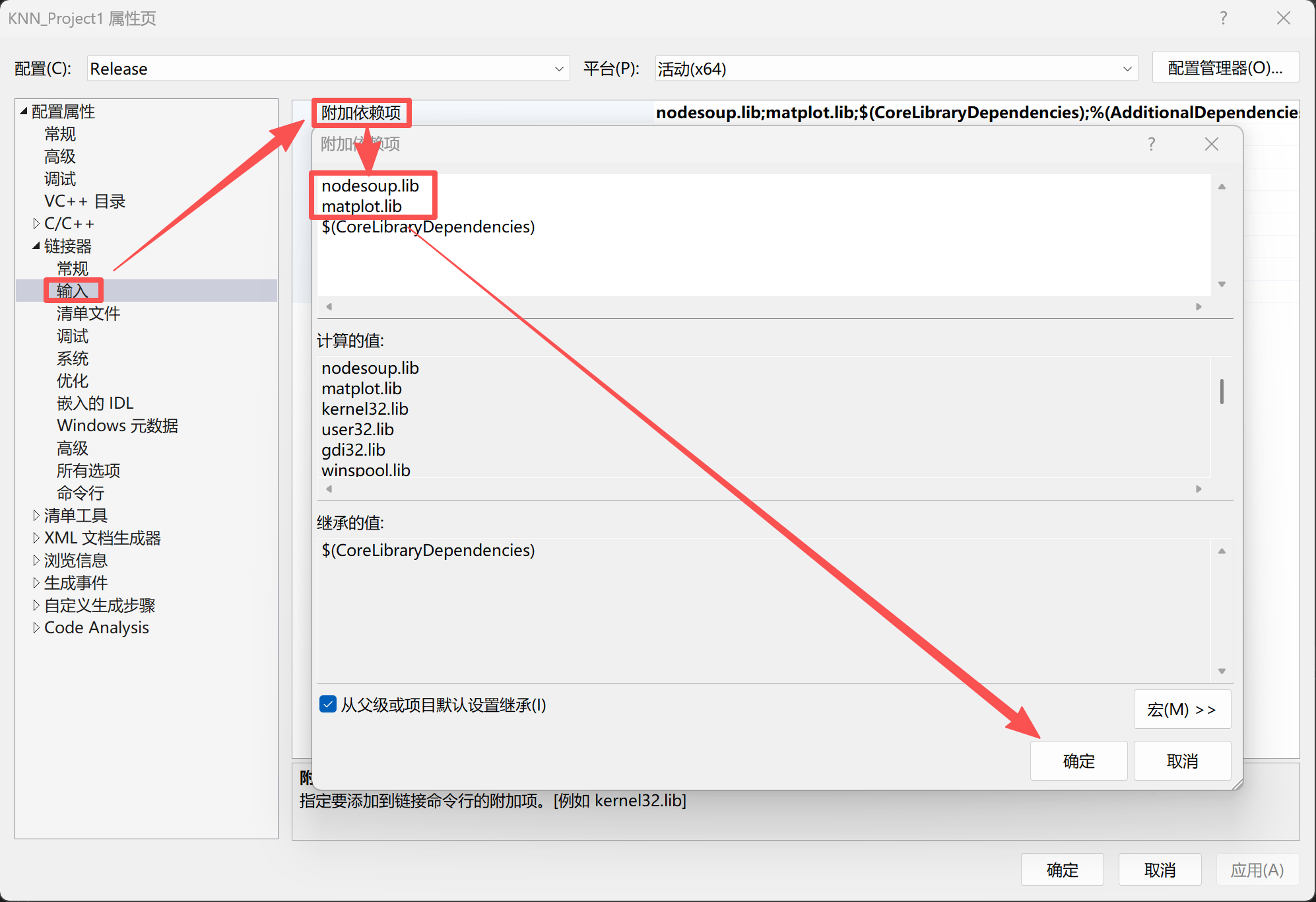
到这里配置完毕

5.1.2.3 premake配置（可以代替5.1.2.2）

可以使用别人写好的premake5.exe文件执行lua文件，帮助我们快速稳定的配置，内容比较多，这里就不展开讲了，有兴趣的读者可以自己去研究一下。

5.2 代码实现

5.2.1 使用的头文件

#include <iostream>
#include <fstream>
#include <vector>
#include <memory>
#include <functional>
#include <algorithm>
#include <unordered_map>
#include <random>
#include <numeric>
#include <queue>
#include <matplot/matplot.h>

tips：不要使用using namespace std; ，因为matplot.h里面也有std作用域，会起冲突。

5.2.2 使用结构体

C++里面也有类，但是这个项目太小了，而且因为C语言太底层了，所以被迫使用C++来写，用STL来加速实现，更主要的是，它是从汇编层面优化的速度，就算小编把C语言和数据结构、算法利用到极限，也很难比拟，所以只能使用C++了。

struct Data
{
	// 为什么不用vector<double>，KNN算法需要频繁访问内存的，使用vector管理反而更慢
	double length;
	double game_time;
	double ice_crime_eating;
	int type;
};

Data结构体的前三个成员均为double类型，为什么不用vector管理呢？

vector是将数据分散存储到堆区，类似链表结构体，到时候我们需要频繁地访问这些数据 ，需要不停使用指针访问内存，会让访问效率下降。

5.2.3 导入数据

std::vector<Data> loadData(const std::string& filepath)
{
	std::ifstream ifs;
	ifs.open(filepath, std::ios::in);
	if (!ifs.is_open())
		throw std::invalid_argument("Failed to open file: " + filepath);

	std::vector<Data> datalist;
	double trail, game, eating;
	std::string tag;

	std::vector<std::string> searchlist =
	{
		"largeDoses",
		"smallDoses",
		"didntLike"
	};

	while (ifs >> trail >> game >> eating >> tag)
	{
		int type = -1;
		for (int i = 0; i < searchlist.size(); ++i)
		{
			if (searchlist[i] == tag)
			{
				type = i;
				break;
			}
		}
		datalist.push_back({ trail, game, eating, type });
	}
	ifs.close();

	return datalist;
}

上文说过，匹配类别对应的字符串，转换成整型数据管理。

5.2.4 预处理

5.2.4.1 归一化

// 更新归一化数据
void calculate(std::vector<double>& feature)
{
	double max = *max_element(feature.begin(), feature.end());
	double min = *min_element(feature.begin(), feature.end());

	double range = max - min;
	for (double& val : feature)
		val = (val - min) / range;
}

// 归一化
void normalized(std::vector<Data>& data)
{
	if (data.empty())
	{
		std::cout << "nullptr doesn't normalized!" << std::endl;
		__debugbreak();
		return;
	}

	std::vector<std::pair<
		std::function<double(const Data&)>,
		std::function<void(Data&, double)>
		>> field =
	{
		{
			[](const Data& d) {return d.game_time; },
			[](Data& d, double val) {d.game_time = val; }
		},
		{
			[](const Data& d) {return d.ice_crime_eating; },
			[](Data& d, double val) {d.ice_crime_eating = val; }
		},
		{
			[](const Data& d) {return d.length; },
			[](Data& d, double val) {d.length = val; }
		}
	};

	for (auto& f : field)
	{
		auto& getVal = f.first;
		auto& setVal = f.second;

		std::vector<double> values;
		for (const auto& d : data)
			values.push_back(getVal(d));

		calculate(values);
		for (int i = 0; i < data.size(); ++i)
			setVal(data[i], values[i]);
	}
}

这里是使用了lamda来简化三个特征维度的归一化实现。

5.2.4.2 洗牌

// 打乱数据
std::vector<Data> shuffleData(std::vector<Data>& data)
{
	auto shuffle_data = std::vector<Data>(data.begin(), data.end());
	std::random_device rd;
	std::mt19937 g(rd());
	std::shuffle(shuffle_data.begin(), shuffle_data.end(), g);

	return shuffle_data;
}

随机生成伪随机数种子，使用shuffle洗牌。

5.2.5 选择最佳k值

5.2.5.1 计算欧几里得距离

// 计算欧几里得距离
double eucliDistance(Data x, Data y)
{
	double trail = x.length - y.length;
	double play = x.game_time - y.game_time;
	double eating = x.ice_crime_eating - y.ice_crime_eating;

	return trail * trail + play * play + eating * eating;
}

5.2.5.2 获取邻居各类别的数量

std::vector<int> getKNeighborProb(const Data& test, const std::vector<Data>& trains, int k)
{
	if (trains.empty() || k <= 0)
		throw std::invalid_argument("Invalid input for getNeighborProb!");
	std::priority_queue<std::pair<double, int>> maxHeap; // 使用最大堆存储
	for (const auto& d : trains)
	{
		double dist = eucliDistance(test, d);
		if (maxHeap.size() < k)
			maxHeap.emplace(dist, d.type);
		else if (maxHeap.top().first > dist)
		{
			maxHeap.pop();
			maxHeap.emplace(dist, d.type);
		}
	}

	std::vector<int> neighborProb(3, 0);
	while (!maxHeap.empty())
	{
		neighborProb[maxHeap.top().second]++;
		maxHeap.pop();
	}

	return neighborProb;
}

由于最大的k个邻居与他们的位置无关 ，我们只需要使用最大堆 把最大的k个邻居和它们的类别存起来，统计最大堆前k个最大邻居出现的类别的数量即可。这里的neighborProb的下标还藏着类别的信息，所以直接算对应下标对应的数量，就能达到目的。

5.2.5.3 选择出现最多的类别作为预测结果

// 预测类型
int predicType(const Data& test, std::vector<Data>& data, int k)
{
	auto vote = getKNeighborProb(test, data, k);
	return max_element(vote.begin(), vote.end()) - vote.begin();
}

找到最大值的下标，减去最小的下标算出偏移量

5.2.5.4 使用k折交叉验证计算准确率和三分类混淆矩阵

// 使用K折交叉验证计算准确率
std::pair<double, std::vector<std::vector<int>>> kFoldCrossVaild(std::vector<Data>& shuffle_data, int kfold, int knn_k)
{
	if (shuffle_data.empty())
		throw std::invalid_argument("Invalid input for countRoc: Null data is invaild!");

	if (kfold <= 0)
		throw std::invalid_argument("Invalid input for countRoc: kfold must be bigger than 0!");

	std::vector<std::vector<int>> cntlist(3, std::vector<int>(3, 0));
	int foldSize = shuffle_data.size() / kfold;
	std::vector<double> accuracies;
	for (int fold = 0; fold < kfold; ++fold)
	{
		int start = fold * foldSize;
		int end = (kfold -1 == fold) ? shuffle_data.size() : start + foldSize;
		int correct = 0;

		std::vector<Data> trainData(shuffle_data.begin(), shuffle_data.begin() + start);
		trainData.insert(trainData.end(), shuffle_data.begin() + end, shuffle_data.end());
		for(int i = start; i < end; ++i)
		{
			auto t = shuffle_data[i];
			int res = predicType(t, trainData, knn_k);
			cntlist[t.type][res]++;
			correct += (res == t.type);
		}
		double accuracy = static_cast<double>(correct) / foldSize;
		accuracies.push_back(accuracy);
	}

	return std::make_pair(std::accumulate(accuracies.begin(), accuracies.end(), 0.0) / kfold , cntlist);
}

统计正确被预测的测试集数量，除以总量获得准确率

5.2.5.5 网格搜索

// 获取最佳的K值
std::pair<int, std::vector<std::vector<int>>> getBestK(std::vector<Data>& data)
{
	if (data.empty())
		throw std::invalid_argument("Invalid input for getBestK: data is null");

	std::vector<double> k;
	std::vector<std::vector<std::vector<int>>> lst;
	for (int i = 3; i < sqrt(data.size()); i += 2)
	{
		auto [res, list] = kFoldCrossVaild(data, 10, i);
		k.push_back(res);
		lst.push_back(list);
	}
	int offset = max_element(k.begin(), k.end()) - k.begin();
	int knn_k = offset * 2 + 3;
	std::cout << "k = " << knn_k << " accuracy = " << k[offset] << std::endl;

	return std::make_pair(knn_k, lst[offset]);
}

从3开始，跳过偶数，偶数可能会平票，所以步长为2，取数据集总量的开方，减少不必要的计算成本。将得到的准确率和混淆矩阵存起来（被迫的空间开销），跑完网格搜素后寻找最大的准确率，换算k值，返回k和混淆矩阵。

5.2.6 计算FPR和TPR

5.2.6.1 将多类型数量转换为概率

// 计算测试集在训练集上的多类型概率
std::vector<double> predicProb(const Data& test, std::vector<Data>& data, int k)
{
	auto vote = getKNeighborProb(test, data, k);
	std::vector<double> appearance(3, 0);
	for (int i = 0; i < appearance.size(); ++i)
		appearance[i] = static_cast<double>(vote[i]) / k;

	return appearance;
}

遍历vector容器，将所有数据除以k

5.2.6.2 计算某一类型作为正例时单个点的FPR和TPR

// 使用K折交叉验证，计算ROC图数据
std::pair<double, double> countRoc(std::vector<Data>& shuffle_data, int kfold, int knn_k, double confd, int genre)
{
	if (shuffle_data.empty())
		throw std::invalid_argument("Invalid input for countRoc: Null data is invaild!");

	if (kfold <= 0)
		throw std::invalid_argument("Invalid input for countRoc: kfold must be bigger than 0!");

	int foldSize = shuffle_data.size() / kfold;
	int TP = 0, FP = 0, FN = 0, TN = 0;
	for (int fold = 0; fold < kfold; ++fold)
	{
		int start = fold * foldSize;
		int end = (kfold - 1 == fold) ? shuffle_data.size() : start + foldSize;
		int correct = 0;

		std::vector<Data> trainData;
		trainData.reserve(shuffle_data.size() - foldSize);
		trainData.assign(shuffle_data.begin(), shuffle_data.begin() + start);
		trainData.insert(trainData.end(), shuffle_data.begin() + end, shuffle_data.end());

		for (int i = start; i < end; ++i)
		{
			auto t = shuffle_data[i];
			std::vector<double> res = predicProb(t, trainData, knn_k);
			bool isPred = (res[genre] >= confd);
			bool isTrue = (genre == t.type);
			TP += isPred && isTrue;
			FP += isPred && (!isTrue);
			FN += (!isPred) && isTrue;
			TN += (!isPred) && (!isTrue);
		}
	}
	
	double TPR = ( TP+FN == 0 ? 0.0 : static_cast<double>(TP) / (TP + FN));
	double FPR = ( FP+TN == 0 ? 0.0 : static_cast<double>(FP) / (FP + TN));

	return { TPR, FPR };
}

5.2.6.3 将某一类别所有点数据整理补全起来

// 组织ROC图数据并补全
std::pair<std::vector<double>, std::vector<double>> getROC(std::vector<Data>& data, int kfold, int knn_k, int genre)
{
	std::vector<double> tprlist;
	std::vector<double> fprlist;
	for (double confd = 1.0; confd > 0; confd -= 0.05)
	{
		auto [tpr, fpr] = countRoc(data, kfold, knn_k, confd, genre);
		tprlist.push_back(tpr);
		fprlist.push_back(fpr);
	}
	if (!(tprlist.front() == 0 && fprlist.front() == 0))
	{
		tprlist.insert(tprlist.begin(), 0);
		fprlist.insert(fprlist.begin(), 0);
	}
	if (!(tprlist.back() == 1 && fprlist.back() == 1))
	{
		tprlist.push_back(1);
		fprlist.push_back(1);
	}

	return { fprlist, tprlist };
}

为什么需要补全？

可能出现FPR不为0和不为1的情况，这样面积就可能会少算一部分（最小FPR的左边区域和最大FPR的右边区域）。

5.2.7 计算AUC

// 累加AUC得到最终值 结合8使用 data十分有序，无需处理即可使用
double getAUC(std::pair<std::vector<double>, std::vector<double>>& data)
{
	double auc = 0.0;

	auto& fprs = data.first;
	auto& tprs = data.second;
	for (int i = 0; i < fprs.size()-1; ++i)
	{
		auc += (fprs[i + 1] - fprs[i]) * (tprs[i + 1] + tprs[i]) / 2;
	}

	std::cout << auc << std::endl;
	return auc;
}

由于我们的getROC函数输入了一连串单向降低的置信度，所以得到的点集是有序的，无需担心不是FPR轴相近的两个点算AUC，且置信度从1到0的过程中，FPR和TPR都是单调递增的，公式不用取绝对值。

5.2.8 可视化

void plotEvalution(std::vector<std::pair<std::vector<double>, std::vector<double>>> data, std::vector<double> aucs, std::vector<std::vector<int>>& list)
{
    using namespace matplot;
    std::vector<std::string> colorList({ "blue", "yellow", "green", "red" });
    std::vector<std::string> tagName({ "largeDoses", "smallDoses", "didntLike", "Random Guess" });

    auto fig = figure(true); // 设置为true是能正常使用figure的关键
    fig->size(2560, 1000);

    subplot(1, 2, 1);
    hold(on);
    for (int i = 0; i < data.size(); ++i)
    {
        plot(data[i].first, data[i].second)->line_width(2).line_style("-").color(colorList[i]);
    }
    plot(std::vector{ 0,1 }, std::vector{ 0,1 })->line_width(1).line_style("--").color(colorList[3]);
    hold(off);

    xlabel("False Positive Rate");
    ylabel("True Positive Rate");
    title("ROC");
    xlim({ 0, 1 });
    ylim({ 0, 1 });

    for (int i = 0; i < aucs.size(); ++i)
        text(0.02, 0.1 - i * 0.025, tagName[i] + " AUC: " + std::to_string(aucs[i]))->font_size(8);
    auto l = ::matplot::legend(tagName);
    l->location(legend::general_alignment::bottomright);
    l->num_rows(2);
    l->font_size(5);

    subplot(1, 2, 2);
    heatmap(list)->normalization(matrix::color_normalization::columns);
    title("Three distribution");
    auto ax = gca();
    ax->x_axis().ticklabels({ "largeDoses", "smallDoses" , "didntLike" });
    ax->y_axis().ticklabels({ "largeDoses", "smallDoses" , "didntLike" });
    ax->x_axis().label_font_size(5);
    ax->y_axis().label_font_size(5);

    //save("ROC.png");
    show();
}

suplot(1, 2, 1)下面的是ROC曲线可视化

suplot(1, 2, 2)下面的是热力图可视化

我就不详细讲解matplot++函数的使用了。可参考官网

5.2.9 mian函数调用

int main()
{
	auto data = loadData("source\\datingTestSet.txt");
	normalized(data);
	auto shuffle_Data = shuffleData(data);
	auto [best_k, list] = getBestK(data);

	std::vector<std::pair<std::vector<double>, std::vector<double>>> results;
	std::vector<double> AUCs;
	for (int i = 0; i < 3; ++i)
	{
		auto res = getROC(shuffle_Data, 10, best_k, i);
		auto auc = getAUC(res);
		results.push_back(res);
		AUCs.push_back(auc);
	}
	plotEvalution(results, AUCs, list);

	return 0;
}

这里有三个类别，也就是可以有三个模型，需要使用循环生成评估数据。

5.3 运行结果展示

六、Python实现

Python的可视化明显比C++第三方库好用多了，我没一两个小时就研究出来怎么可视化了

而且配置环境也简单很多

6.1 环境准备

6.1.1 在虚拟环境中配置环境

在你的新的虚拟环境中，安装numpy和matplotlib

conda install numpy
conda install matplotlib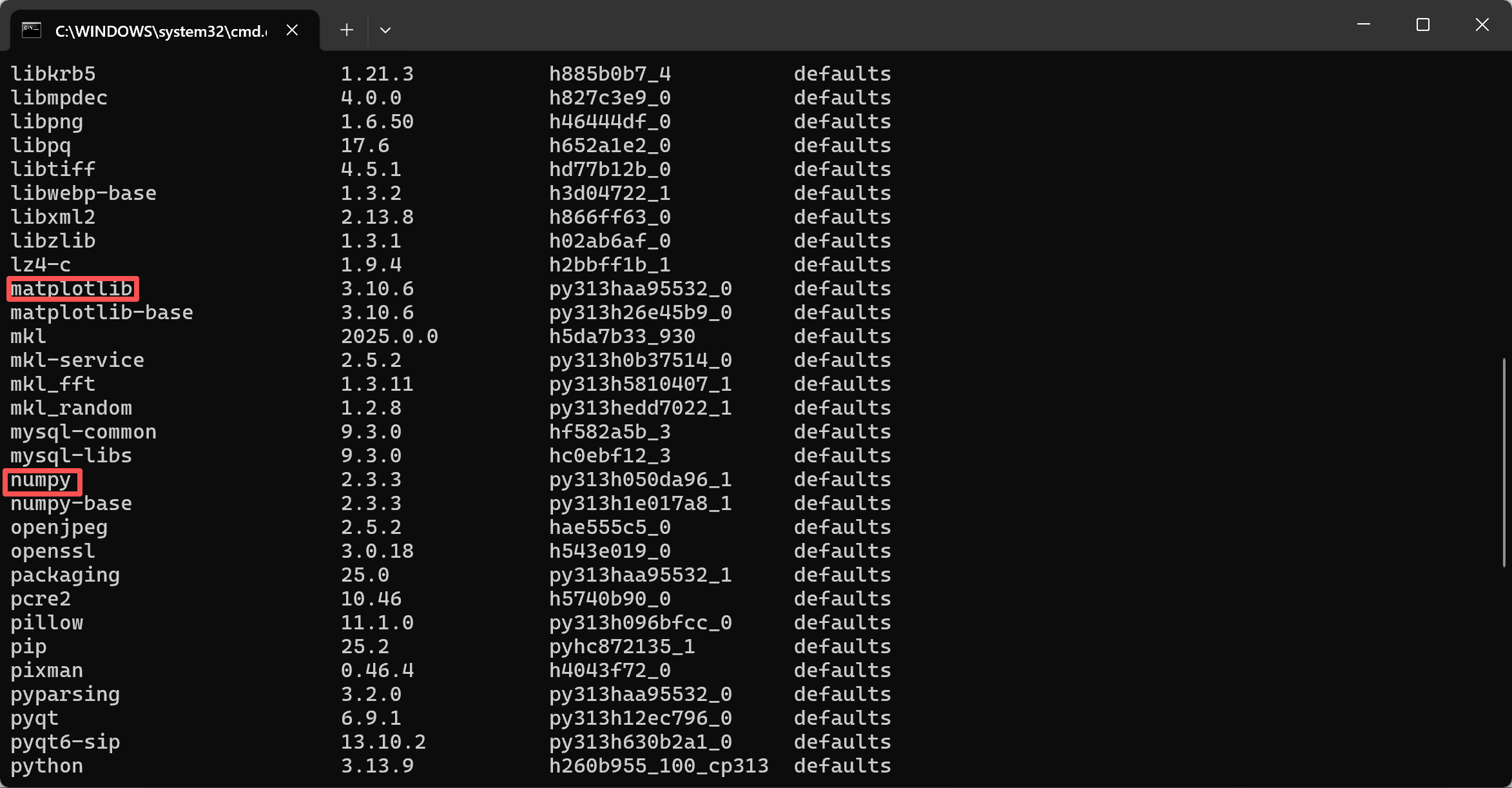

6.1.2 配置Pycharm

创建时选择conda环境，到你的anaconda的文件夹中找到虚拟环境对应的python.exe

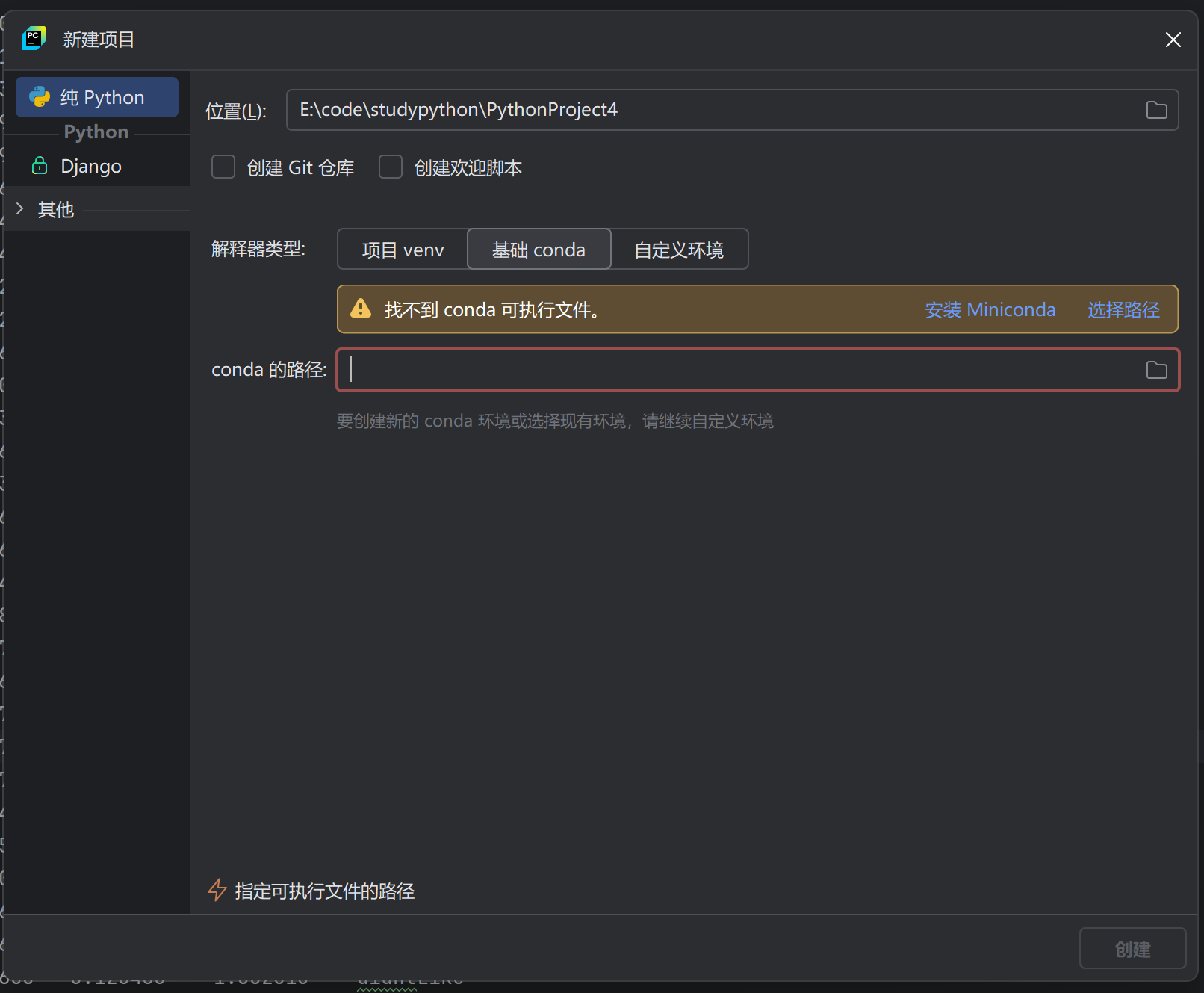
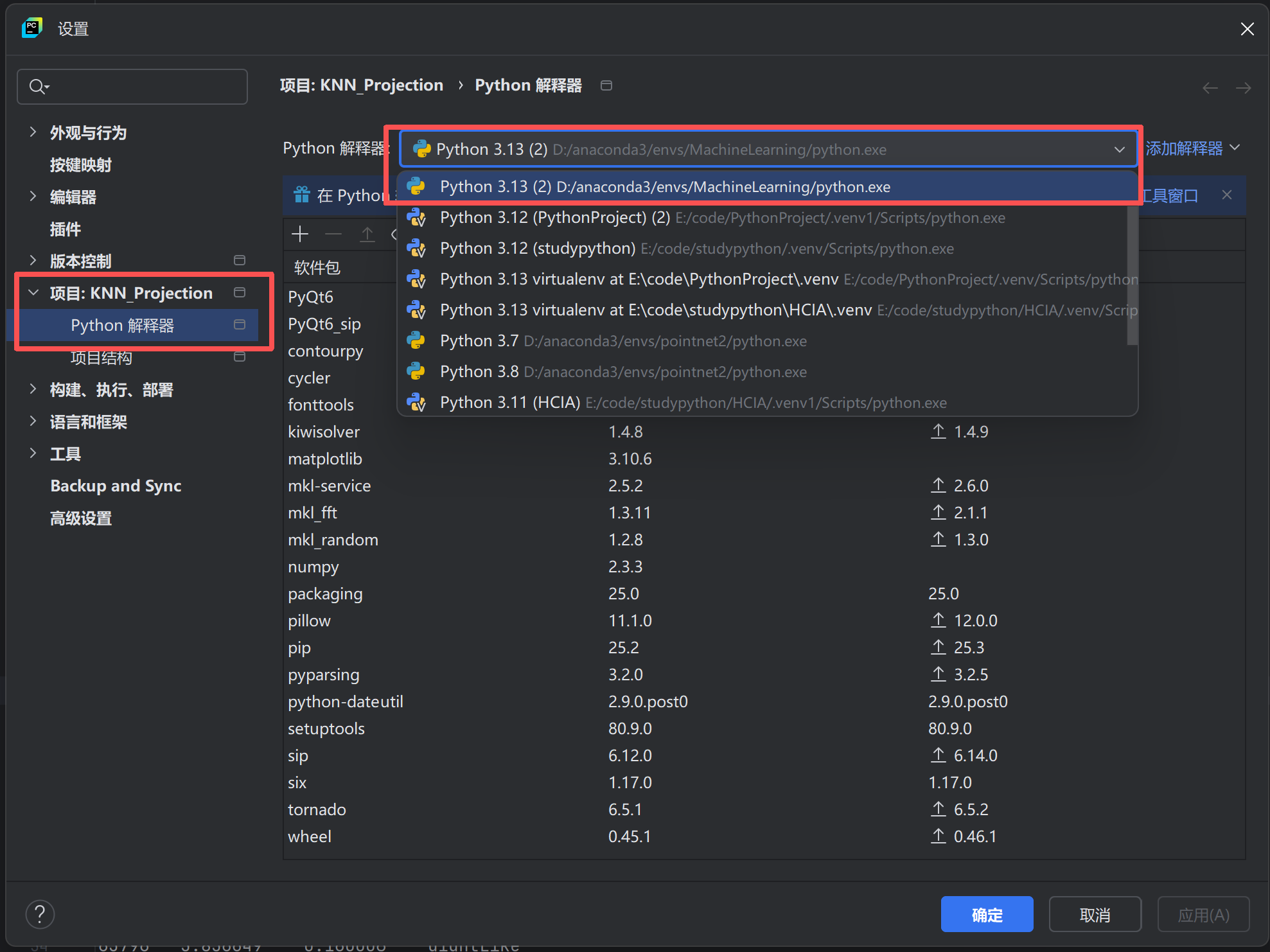
6.2 代码实现

import numpy as np
import matplotlib.pyplot as plt

tag_map = {
    "largeDoses": 0,
    "smallDoses": 1,
    "didntLike": 2
}

# 导入数据
def load_data(filepath):
    # 读取数据
    data = []
    with open(filepath, 'r', encoding="utf-8") as f:
        for line in f:
            line = line.strip()
            if not line:
                continue
            parts = line.split('\t')
            if len(parts) != 4:
                print(f"特征数据无法转换：{line}")
                continue
            tag = parts[3]
            data.append({
                "feature": [parts[0], parts[1], parts[2]],
                "tag": tag_map[tag]
            })

    return data

# 归一化 利用numpy的广播机制
def normalized(features: np.ndarray):
    # 获取每一列的最大值和最小值
    max_val = features.max(axis=0)
    min_val = features.min(axis=0)

    ranges = max_val-min_val
    ranges[ranges < 1e-9] = 1.0 # 比较每个列的相减结果，排除0的情况

    return (features-min_val)/ranges

# 计算欧式距离
def euclidean_dist(test, train):
    return np.sum((test - train) ** 2, axis=1)

# 计算各类标签的概率
def predict_prob(test, train_data, k):
    train_features = train_data[:,:3]
    dist = euclidean_dist(test, train_features)
    k_indices = np.argpartition(dist, k)[:k] # 完成一次快速排序
    k_tags = train_data[k_indices, 3].astype(int)
    prob = np.bincount(k_tags, minlength=3) / k
    return prob

# 选择最大概率作为当前测试样本的预测类型
def predict_type(test, train_data, k):
    return max(enumerate(predict_prob(test, train_data, k)), key=lambda x:x[1])[0]

# 使用k折交叉验证，计算准确率和三分类特征混淆矩阵
def k_folds_cross_valid_acc(features: np.ndarray, k, k_fold):
    # 计算每一折的大小
    fold_size = int(len(features)/k_fold)
    fold_accuracies = 0.0
    confusion_mat = np.zeros([3,3], dtype=np.int32)

    for i in range(k_fold):
        start = i*fold_size
        # 防止最后一折不够一折的大小
        end = start+fold_size if i != k_fold-1 else len(features)
        train_data = np.concatenate([features[:start], features[end:]])
        correct = 0
        test_data = features[start:end]
        for t in test_data:
            pred_type = predict_type(t[:3], train_data, k)
            if pred_type == t[3]:
                correct += 1
            confusion_mat[int(t[3])][pred_type] += 1
        fold_accuracies += correct/fold_size
    return fold_accuracies/k_fold, confusion_mat

# 计算模型roc曲线的单个点
def count_roc(features: np.ndarray, k_fold, k_neighbor, confidence, genre):
    fold_size = int(len(features)/k_fold)
    tp, tn, fp, fn = 0, 0, 0, 0

    for i in range(k_fold):
        start = i*fold_size
        end = start+fold_size if i != k_fold-1 else len(features)
        train_data = np.concatenate([features[:start], features[end:]])
        test_data = features[start:end]
        for t in test_data:
            prob = predict_prob(t[:3], train_data, k_neighbor)
            if genre == t[3] and prob[genre] >= confidence:
                tp += 1
            elif genre != t[3] and prob[genre] < confidence:
                tn += 1
            elif genre != t[3] and prob[genre] >= confidence:
                fp += 1
            elif genre == t[3] and prob[genre] < confidence:
                fn += 1

    tpr = tp / (tp+fn) if (tp+fn) else 0.0
    fpr = fp / (fp+tn) if (fp+tn) else 0.0

    return fpr, tpr

# 整理并补全roc曲线的两个点集
def get_roc(features: np.ndarray, k_fold, k_neighbor, genre):
    # 生成1到0步长为-0.05的列表
    confidence = np.arange(1.0, 0, -0.05)
    fpr_list = list()
    tpr_list = list()
    for conf in confidence:
        fpr, tpr = count_roc(features, k_fold, k_neighbor, conf, genre)
        fpr_list.append(fpr)
        tpr_list.append(tpr)

    if fpr_list[0] != 0.0:
        fpr_list.insert(0, 0.0)
        tpr_list.insert(0, 0.0)
    if fpr_list[len(fpr_list)-1] != 1.0:
        fpr_list.append(1.0)
        tpr_list.append(1.0)

    return [fpr_list, tpr_list]

# 获取AUC
def get_auc(result):
    auc = 0.0
    fpr_list, tpr_list = result
    if len(fpr_list) < 2:
        return 0.0
    for i in range(len(fpr_list)-1):
        # 梯形法算AUC面积
        auc += (fpr_list[i+1]-fpr_list[i])*(tpr_list[i]+tpr_list[i+1])/2
    return auc

# 通过值寻找键列表
def get_value(dictionary: dict, target_value: int):
    return [key for key, value in dictionary.items() if value == target_value]

# 绘制roc曲线
def plot_roc(results, ax):
    class_names = list(tag_map.keys())
    for i in range(len(results)):
        ax.plot(results[i][0], results[i][1], linewidth=2, label=f"{class_names[i]} AUC: {results[i][2]:0.5f}")
    ax.plot((0, 1), (0, 1), "--", linewidth=1, label="predicted line")

    ax.legend(loc="lower right")
    ax.set_title("ROC Curve")
    ax.set_xlabel("False Positive Rate")
    ax.set_ylabel("True Positive Rate")
    ax.set_xlim(0,1)
    ax.set_ylim(0,1)

# 绘制热力图
def plot_heatmap(heat_conf, ax):
    class_names = list(tag_map.keys())
    im = ax.imshow(heat_conf)
    ax.set_xticks(range(len(class_names)))
    ax.set_xticklabels(labels=tag_map.keys(), rotation=45, ha="right", rotation_mode="anchor")
    ax.set_yticks(range(len(class_names)))
    ax.set_yticklabels(labels=tag_map.keys())
    ax.set_title("Three Distribution")

    for i in range(len(tag_map)):
        for j in range(len(tag_map)):
            value = heat_conf[i, j]
            # 提高可视化观感
            text_color = "black" if im.norm(value) > 0.5 else "white"
            ax.text(j, i, value, ha="center", va="center", color=text_color, fontweight="bold")

    cbar = plt.colorbar(im, ax=ax)
    cbar.set_label("Sample Count")


if __name__ == "__main__":
    # 导入数据
    dataset = load_data("datingTestSet.txt")
    # 检查数据是否导入
    if not dataset:
        print("没有有效数据")
        exit()

    # 创建numpy数组
    feature_list = np.array([d["feature"] for d in dataset], dtype=np.float64)
    tag_list = np.array([d["tag"] for d in dataset], dtype=np.int32)

    # 归一化数组
    normalized_feature = normalized(feature_list)

    # 将特征和标签拼接
    tag_list = tag_list.reshape(-1, 1) # 将numpy数组转置
    feature_tag = np.hstack((normalized_feature, tag_list))

    # 洗牌
    np.random.seed(42)
    np.random.shuffle(feature_tag)

    # 选择最大准确率，选择最佳k值，并计算出最佳k值下的三分类特征混淆矩阵
    best_k = 0
    best_acc = 0
    best_confusion = np.zeros([3, 3], dtype=np.int32)
    for i in range(3, int(np.sqrt(len(feature_tag))), 2):
        acc, confusion = k_folds_cross_valid_acc(feature_tag, i, 10)
        if best_acc < acc:
            best_k = i
            best_acc = acc
            best_confusion = confusion
    print(f"十折交叉验证的最佳k值为：{best_k}，对应的准确率为：{best_acc:0.5f}")

    # 评估模型：获取ROC曲线和AUC值
    results = list()
    for i in range(3):
        res = get_roc(feature_tag, 10, best_k, i)
        auc = get_auc(res)
        results.append([*res, auc])

    # 评估数据可视化
    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
    plot_roc(results, ax1)
    plot_heatmap(best_confusion, ax2)

    plt.tight_layout()
    plt.show()

由于算法实现和C++版的类似，且小编给出的代码注释清晰，在一些函数边上也有注释使用原因，所以不再赘述。

matplotlib官方使用说明
numpy官方使用说明

6.3 运行效果展示

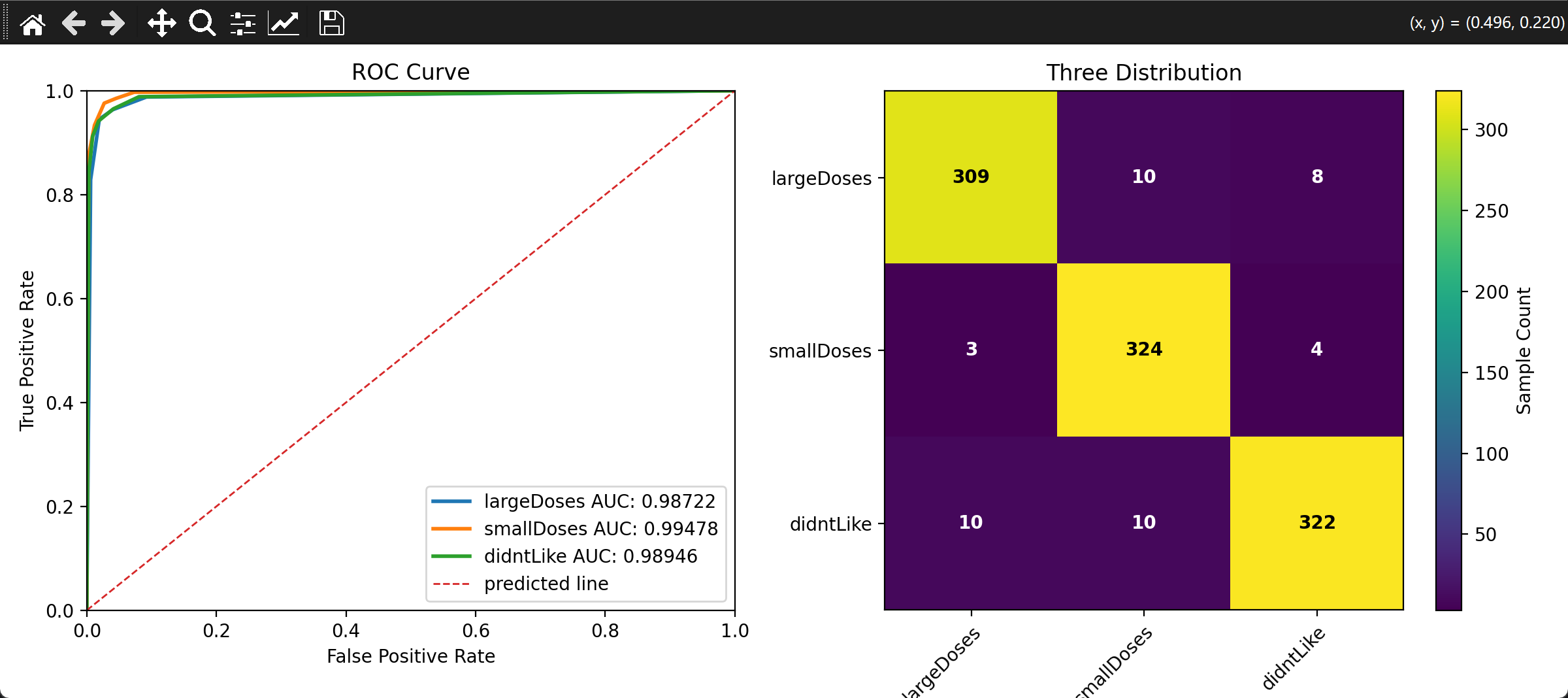
七、总结

通过实现C++，我们可以更加深刻的了解KNN算法的原理；

通过实现Python，我们可以更明白为什么Python更适合做与人工智能相关的工作；

通过实现本文的内容，我对C++配置文件的理解更加深刻了；

相信读者也能从这么一篇详细的博客学到点东西。