C++：红黑树

红黑树

一.初识红黑树
- 1.红黑树的概念
- 2.红黑树的核心规则
- 3.说明
- 4.红黑树的效率分析
二.红黑树的简单模拟实现
- 1.红黑树节点结构
- - 代码解释
- 2.红黑树的插入
- - （1）空树处理
  - （2）二叉搜索树插入逻辑
  - （3）插入后平衡调整（核心）
  - - 场景1：父节点是祖父节点的左孩子（`grandfather->_left == parent`）
    - - 子场景1.1：叔叔存在且为红色（`uncle && uncle->_col == RED`）
      - 子场景1.2：叔叔不存在或为黑色（`!uncle || uncle->_col == BLACK`）
    - 场景2：父节点是祖父节点的右孩子（`grandfather->_right == parent`）
  - （4）最终保证根节点为黑色
  - 总结
- 2.红黑树的查找
- - 2.1 功能
  - 2.2 实现逻辑
- 3.检查红黑树是否平衡
- - 3.1 功能
  - 3.2 实现逻辑
- 1. 红黑树的基础操作封装（节点总数、高度与中序遍历）
- - 4.1 功能
  - 4.2 实现逻辑
- 5.红黑树的递归工具函数（节点总数与高度计算）
- - 5.1 函数功能与实现
- 6.测试代码
- - 测试说明：
  - 预期结果：

一.初识红黑树

1.红黑树的概念

红黑树是一种自平衡的二叉搜索树，其每个结点除了存储数据外，还增加一个额外的存储位表示颜色（红色或黑色）。通过对结点颜色的约束，红黑树能保证从根到任意叶子的路径长度差不超过两倍，从而维持近似平衡的状态，避免二叉搜索树在极端情况下退化为链表（如有序插入时），确保增删查改操作的时间复杂度稳定在O(log n)。

2.红黑树的核心规则

红黑树的平衡通过以下5条规则严格约束（整合经典定义，明确空结点处理）：

颜色约束：每个结点要么是红色，要么是黑色。
根结点特性：根结点必须是黑色。
红结点子结点约束：若一个结点是红色，则其两个子结点必须是黑色（即不存在连续的红色结点）。
黑路径平衡 ：从任意结点到其所有空子孙结点（NIL结点） 的每条简单路径上，包含的黑色结点数量相同（称为"黑高"相等）。
空结点颜色：所有空结点（NIL，即叶子的子结点，非传统意义上的叶子）均视为黑色。

3.说明

规则5中提到的"NIL结点"是逻辑上的空结点（可理解为"哨兵结点"），目的是统一路径的终点判定，简化规则4的验证（确保每条路径的黑结点计数起点和终点一致）。实际实现中，有时会省略显式的NIL结点，仅通过逻辑判断处理，但规则的约束本质不变。
这些规则共同保证了红黑树的"近似平衡"：最长路径（红黑交替）不会超过最短路径（全黑）的2倍，从而维持高效的操作性能。

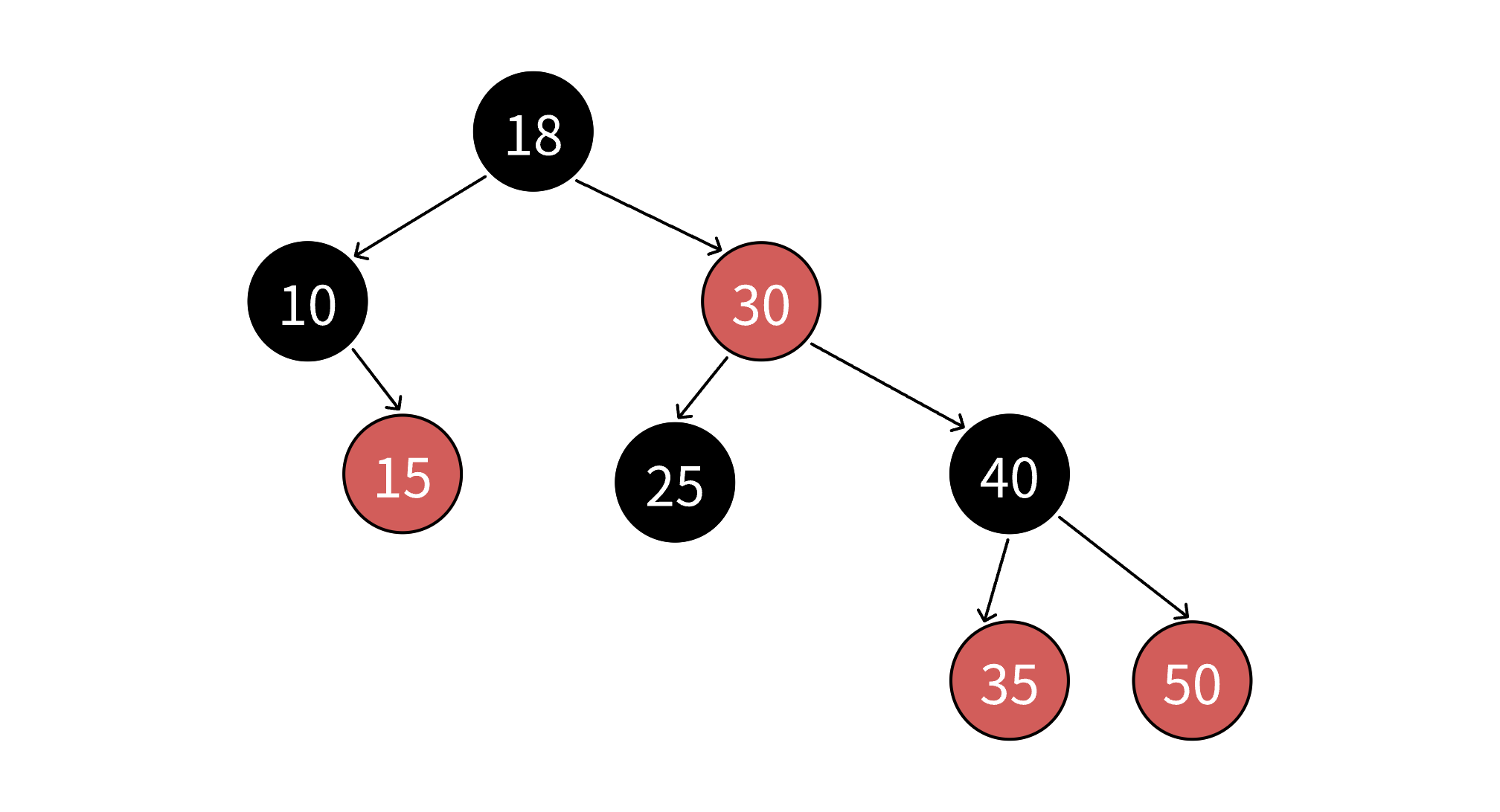
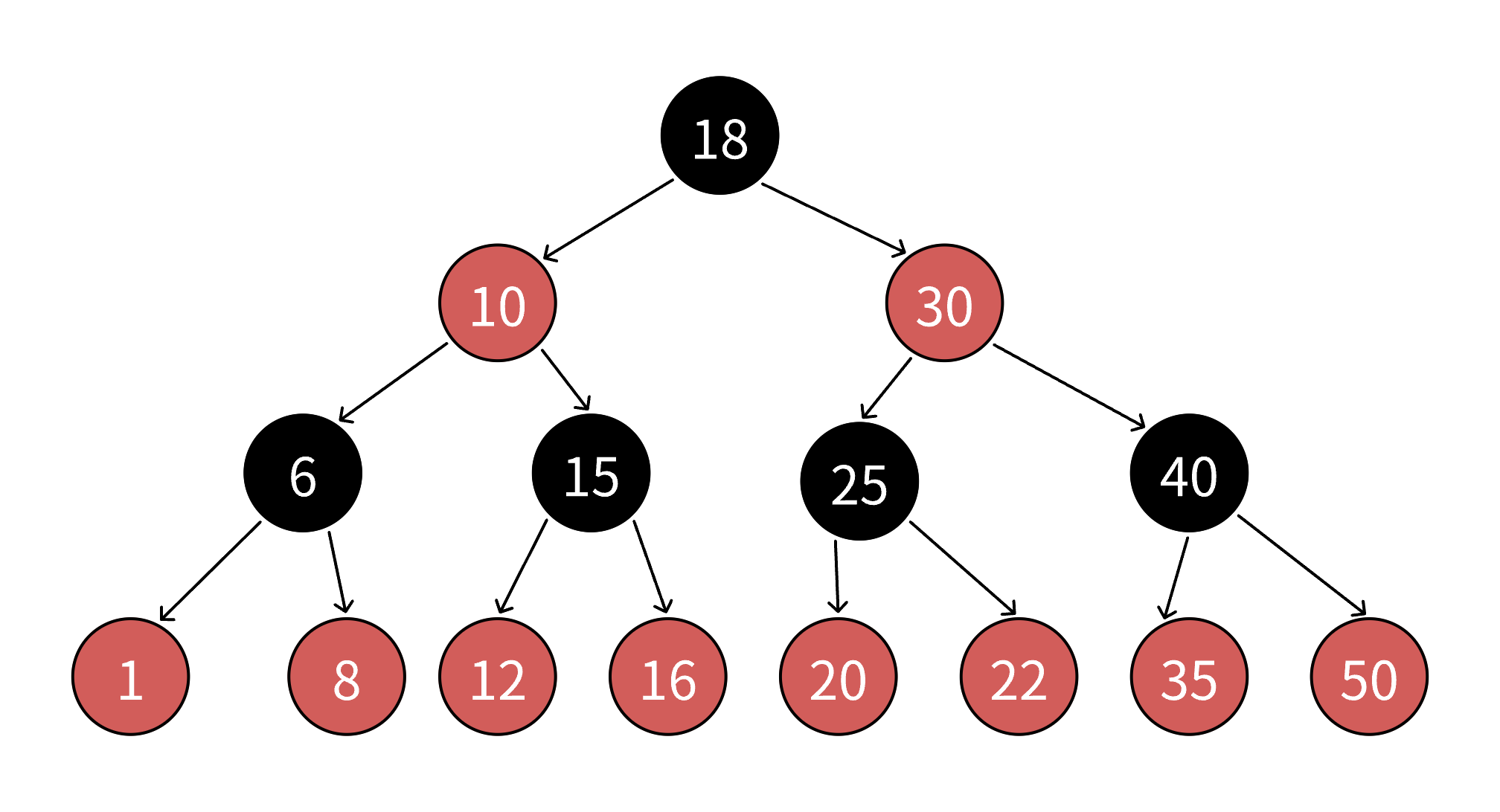
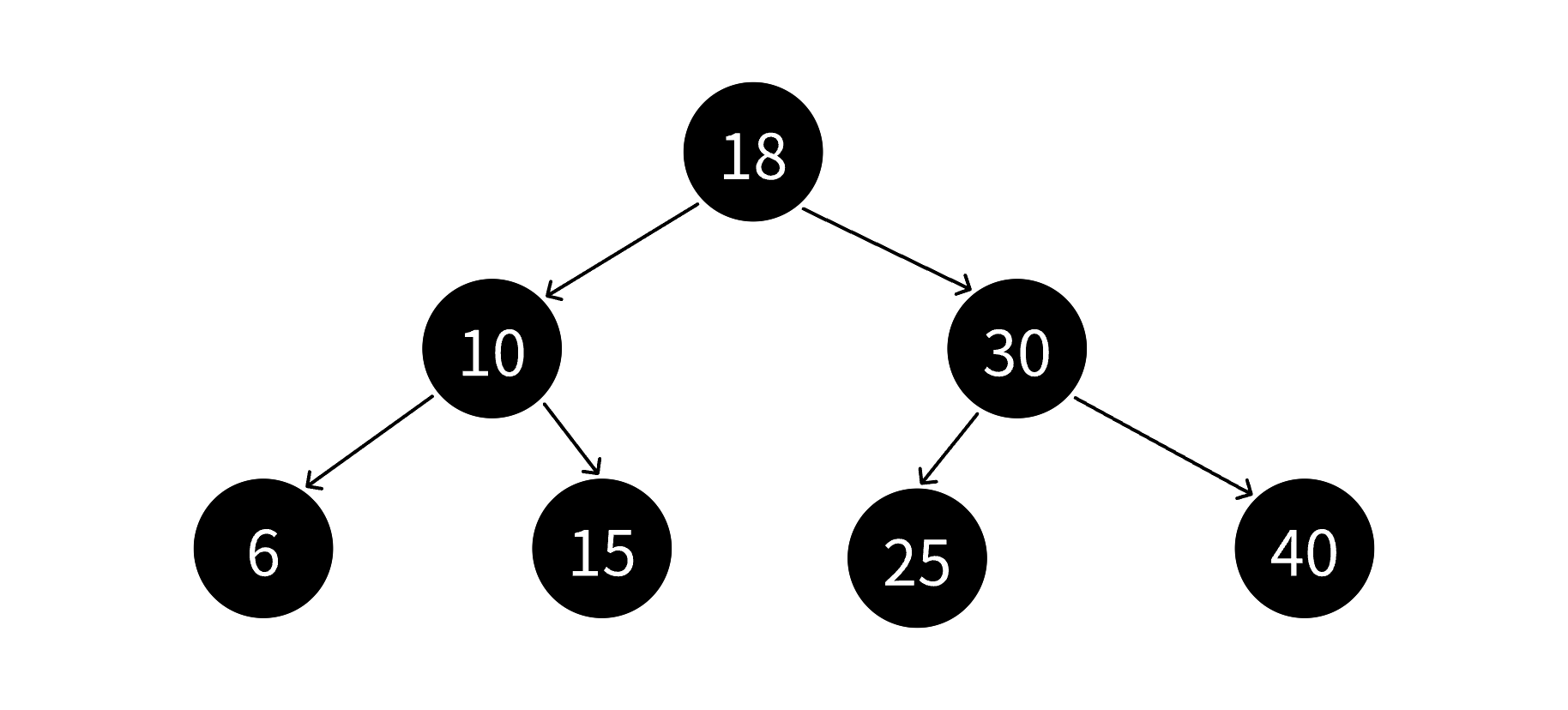
4.红黑树的效率分析

红黑树的核心优势在于通过颜色约束实现近似平衡，从而保证操作的高效性。假设树中节点总数为 ( N )，最短路径（全黑节点构成）的长度为 ( h )（即黑高），可推导出以下关系：

最短路径（全黑节点）的节点数为 ( h )，对应节点总数下限：( N \geq 2^h - 1 )（满二叉树情形）。
最长路径（红黑交替）的节点数不超过 ( 2h )（红色节点最多与黑色节点数量相等），对应节点总数上限：( N < 2^{2h} - 1 )。

由此可推得 ( h \approx \log_2 N )，因此最长路径长度不超过 ( 2\log_2 N )。这意味着红黑树中任意操作（增、删、查、改）的最坏时间复杂度均为 ( O(\log N) )，与完全平衡的二叉树效率同级。

二.红黑树的简单模拟实现

1.红黑树节点结构

cpp 复制代码

#pragma once
#include<iostream>
using namespace std;

// 节点颜色枚举：红色/黑色
enum Color {
	RED,
	BLACK
};

// 红黑树节点模板结构
template<typename K,typename V>
struct RBTreeNode {
	pair<K, V> _kv;               // 存储键值对
	RBTreeNode <K, V>* _left;     // 左子节点指针
	RBTreeNode <K, V>* _right;    // 右子节点指针
	RBTreeNode <K, V>* _parent;   // 父节点指针（红黑树调整需父子关系）
	Color _col;                   // 节点颜色

	// 构造函数：初始化键值对，子节点及父节点指针默认为空
	RBTreeNode(const pair<K, V>& kv)
		:_kv(kv)
		,_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
	{}
};

代码解释

颜色枚举 ：定义了Color枚举类型，包含RED（红色）和BLACK（黑色）两种颜色，用于标识红黑树节点的颜色。
红黑树节点模板结构（RBTreeNode） ：
- 成员变量：包含存储键值对的_kv（类型为pair<K, V>）、指向左子节点的_left、指向右子节点的_right、指向父节点的_parent，以及表示节点颜色的_col。
- 构造函数：接收一个pair<K, V>类型的引用参数，初始化_kv，并将_left、_right、_parent初始化为nullptr。

2.红黑树的插入

cpp 复制代码

template<typename K, typename V>
class RBTree{
typedef RBTreeNode<K, V> Node;
public:
	bool Insert(const pair<K, V>& kv)
	{
		if (!_root)//AVL树为空树的情况
		{
			_root = new Node(kv);
			_root->_col = BLACK;
			return true;
		}
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else return false;
		}
		//走到空位置
		cur = new Node(kv);
		
		if (parent->_kv.first > kv.first) parent->_left = cur;
		else if (parent->_kv.first < kv.first) parent->_right = cur;
		cur->_parent = parent;

		//分情况进行插入调整，变色或旋转
		while (parent && parent->_col == RED)
		{
			Node* grandfather = parent->_parent;  // 获取祖父节点（必存在，否则父红违反规则）

			// 父节点是祖父的左孩子
			if (grandfather->_left == parent)
			{
				Node* uncle = grandfather->_right;  // 叔叔节点（祖父的右孩子）

				// 叔叔存在且为红色（变色处理）
				if (uncle && uncle->_col == RED) 
				{
					parent->_col = uncle->_col = BLACK;  // 父、叔变黑色
					grandfather->_col = RED;             // 祖父变红色

					cur = grandfather;       // 继续向上检查
					parent = cur->_parent;
				}
				// 叔叔不存在或为黑色（旋转处理）
				else
				{
					// 当前节点是父节点的左孩子（右单旋）
					if (cur == parent->_left)
					{
						RotateRight(grandfather);  // 以祖父为轴右旋
						parent->_col = BLACK;      // 父节点变黑
						grandfather->_col = RED;   // 原祖父变红
					}
					// 当前节点是父节点的右孩子（左右双旋）
					else
					{
						RotateLeftRight(grandfather);  // 以祖父为轴左右双旋
						cur->_col = BLACK;             // 当前节点变黑
						grandfather->_col = RED;       // 原祖父变红
					}
					break;  // 旋转后已平衡，退出循环
				}
				 if (grandfather->_right == parent)  // 父节点是祖父节点的右孩子
				{
					Node* uncle = grandfather->_left;  // 叔叔节点为祖父节点的左孩子
					if (uncle && uncle->_col)  // 叔叔节点存在且为红色
					{
						parent->_col = uncle->_col = BLACK;  // 父和叔叔设为黑色
						grandfather->_col = RED;  // 祖父设为红色

						cur = grandfather;  // 继续向上调整
						parent = cur->_parent;
					}
					else  // 叔叔节点不存在或为黑色
					{
						if (cur == parent->_right)  // 当前节点是父节点的右孩子（右右情况）
						{
							RotateLeft(grandfather);  // 左旋转祖父节点
							parent->_col = BLACK;     // 父节点设为黑色
							grandfather->_col = RED;  // 原祖父节点设为红色
						}
						else  // 当前节点是父节点的左孩子（右左情况）
						{
							RotateRightLeft(grandfather);  // 先右旋转父节点，再左旋转祖父节点
							cur->_col = BLACK;             // 当前节点设为黑色
							grandfather->_col = RED;       // 原祖父节点设为红色
						}
						break;  // 调整完成，退出循环
					}
				}
			}
		}
		_root->_col = BLACK;
			return true;
		}

template<typename K, typename V> class RBTree：红黑树类模板，键类型为K，值类型为V。
typedef RBTreeNode<K, V> Node：简化节点类型名，Node即红黑树节点结构（包含键值对、左右子节点、父节点指针及颜色）。

（1）空树处理

若树为空（_root为nullptr），直接创建新节点作为根，并将根节点颜色设为黑色（符合红黑树规则2：根为黑色）。

（2）二叉搜索树插入逻辑

非空树时，先通过二叉搜索树规则查找插入位置：
从根节点_root出发，用cur遍历，parent记录cur的父节点。
- 若cur->_kv.first > kv.first：向左子树查找；
- 若cur->_kv.first < kv.first：向右子树查找；
- 若相等：插入失败（键值唯一）。
找到空位置后，创建新节点cur，根据键值大小设为parent的左/右孩子，并绑定parent指针（新节点默认颜色为红色，代码未显式写但红黑树插入新节点通常为红色，因红色对平衡影响更小）。

（3）插入后平衡调整（核心）

新节点为红色，若其父节点parent为黑色，无需调整（不违反规则）；若parent为红色（违反规则3：连续红色节点），则需进入循环调整，直到不违反规则。

循环条件：parent && parent->_col == RED（父节点存在且为红色，需调整）。

调整逻辑分两大场景（父节点是祖父节点的左/右孩子，对称处理）：

场景1：父节点是祖父节点的左孩子（`grandfather->_left == parent`）

祖父节点grandfather：必存在且为黑色（因父节点为红色，若祖父为红则违反规则3，故祖父一定是黑）。
叔叔节点uncle：祖父的右孩子（与父节点对称）。

子场景1.1：叔叔存在且为红色（`uncle && uncle->_col == RED`）

调整方式：变色。
- 父节点parent和叔叔uncle改为黑色；
- 祖父节点grandfather改为红色（维持黑高平衡：原祖父为黑，父和叔为红，变色后黑节点数量不变）。
继续向上检查：将cur更新为祖父，parent更新为祖父的父节点，重复循环（因祖父变红色后，可能与曾祖父形成连续红色）。

子场景1.2：叔叔不存在或为黑色（`!uncle || uncle->_col == BLACK`）

调整方式：旋转+变色（因叔叔无法通过变色分担红色，需旋转重构树结构）。
- 子场景1.2.1：cur是父节点的左孩子（左左结构）：
  
  执行右旋转 （以祖父为轴），旋转后父节点成为新的子树根；
  
  父节点改为黑色，原祖父改为红色（消除连续红色，维持黑高）。
- 子场景1.2.2：cur是父节点的右孩子（左右结构）：
  
  执行左右双旋 （先左旋父节点，再右旋祖父），旋转后cur成为新的子树根；
  cur改为黑色，原祖父改为红色（消除连续红色，维持黑高）。
- 旋转后局部已平衡，break退出循环。

场景2：父节点是祖父节点的右孩子（`grandfather->_right == parent`）

逻辑与场景1对称，区别在于：
- 叔叔节点uncle是祖父的左孩子；
- 旋转方向相反（左旋转、右左双旋），变色规则一致。

（4）最终保证根节点为黑色

无论调整过程如何，最后强制将根节点设为黑色（确保符合规则2）。

总结

该函数通过"二叉搜索树插入+红黑规则校验+变色/旋转调整"，实现了红黑树的插入操作，确保插入后仍满足红黑树的5条规则，维持近似平衡，保证操作效率为O(log n)。

2.红黑树的查找

注：红黑树的查找和AVL树，二叉平衡搜索树的查找一致

cpp 复制代码

		// 查找键对应节点，返回节点指针（未找到返回nullptr）
		Node* Find(const K& key)
		{
			Node* cur = _root;
			while (cur)
			{
				if (cur->_kv.first > key)  // 键值小于当前节点，向左查找
				{
					cur = cur->_left;
				}
				else if (cur->_kv.first < key)  // 键值大于当前节点，向右查找
				{
					cur = cur->_right;
				}
				else  // 找到目标节点
				{
					return cur;
				}
			}
			return nullptr;  // 未找到
		}

2.1 功能

该函数用于在红黑树中查找指定键key对应的节点，属于红黑树的核心查询操作。

2.2 实现逻辑

初始化cur指针指向根节点_root。
循环遍历树结构：
- 若当前节点cur的键值大于目标key，则向左子树查找（cur = cur->_left）；
- 若当前节点cur的键值小于目标key，则向右子树查找（cur = cur->_right）；
- 若键值相等，说明找到目标节点，返回cur；
若循环结束仍未找到，返回nullptr。

3.检查红黑树是否平衡

cpp 复制代码

// 检查平衡树
	bool IsBalanceTree() {
		if (!_root) return true;  // 空树默认平衡

        // 根节点必须为黑色
		if (_root->_col == RED) {
			cout << "根节点为红色，红黑树不平衡" << endl;
			return false;
		}

		// 计算最左路径的黑色节点数（作为参考值）
		Node* leftMost = _root;
		int blackNumRef = 0;
		while (leftMost) {
			if (leftMost->_col == BLACK) {
				blackNumRef++;
			}
			leftMost = leftMost->_left;
		}

		int blackNum = 0;  // 用于递归中累计黑色节点数
		return Check(_root, blackNum, blackNumRef);
	}

3.1 功能

用于检查红黑树是否满足所有红黑树规则，确保树的平衡状态。

3.2 实现逻辑

空树处理 ：若树为空（_root为nullptr），默认返回平衡（true）。
根节点颜色检查：红黑树规则要求根节点必须为黑色，若根节点为红色，直接判定不平衡并输出提示。
基准黑节点数计算 ：遍历最左路径，统计黑色节点数量（blackNumRef），作为后续路径黑节点数的参考值。
递归检查 ：调用Check函数（代码中未完全展示，推测用于递归验证所有路径的黑节点数是否与blackNumRef一致，同时检查红节点的子节点是否为黑色等规则）。

4. 红黑树的基础操作封装（节点总数、高度与中序遍历）

cpp 复制代码

	// 获取树的节点总数
	int Size(){return _Size(_root);}

	// 获取树的高度
	int Height(){return _Height(_root);}


	// 中序遍历（按键值升序输出）
	void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}
private:
	Node* _root = nullptr;  // 根节点指针
	
	// 右旋转（解决左左失衡）
	void RotateRight(Node* parent)
	{
		Node* subL = parent->_left;       // 左子树的根节点
		Node* subLR = subL->_right;       // 左子树的右子树
		Node* parentParent = parent->_parent;  // 失衡节点的父节点

		// 1. 调整parent与subLR的关系
		parent->_left = subLR;
		if (subLR)  // 若subLR存在，更新其父指针
		{
			subLR->_parent = parent;
		}

		// 2. 调整subL与parent的关系
		subL->_right = parent;
		parent->_parent = subL;

		// 3. 调整subL与原parent父节点的关系
		if (parentParent)  // 若parent不是根节点
		{
			if (parentParent->_left == parent)  // parent是左孩子
			{
				parentParent->_left = subL;
			}
			else  // parent是右孩子
			{
				parentParent->_right = subL;
			}
			subL->_parent = parentParent;
		}
		else  // parent是根节点，更新根指针
		{
			_root = subL;
			subL->_parent = nullptr;
		}
	}

	// 左旋转（解决右右失衡）
	void RotateLeft(Node* parent)
	{
		Node* subR = parent->_right;      // 右子树的根节点
		Node* subRL = subR->_left;        // 右子树的左子树
		Node* parentParent = parent->_parent;  // 失衡节点的父节点

		// 1. 调整parent与subRL的关系
		parent->_right = subRL;
		if (subRL)  // 若subRL存在，更新其父指针
		{
			subRL->_parent = parent;
		}

		// 2. 调整subR与parent的关系
		subR->_left = parent;
		parent->_parent = subR;

		// 3. 调整subR与原parent父节点的关系
		if (parentParent)  // 若parent不是根节点
		{
			if (parentParent->_left == parent)  // parent是左孩子
			{
				parentParent->_left = subR;
			}
			else  // parent是右孩子
			{
				parentParent->_right = subR;
			}
			subR->_parent = parentParent;
		}
		else  // parent是根节点，更新根指针
		{
			_root = subR;
			subR->_parent = nullptr;
		}
	}

	// 左右旋转（先左旋左子树，再右旋失衡节点，解决左右失衡）
	void RotateLeftRight(Node* parent)
	{
		Node* subL = parent->_left;    // 左子树的根节点
		Node* subLR = subL->_right;    // 左子树的右子树（失衡的关键节点）

		// 1. 先对左子树subL进行左旋
		RotateLeft(subL);
		// 2. 再对失衡节点parent进行右旋
		RotateRight(parent);
	}

	// 右左旋转（先右旋右子树，再左旋失衡节点，解决右左失衡）
	void RotateRightLeft(Node* parent)
	{
		Node* subR = parent->_right;    // 右子树的根节点
		Node* subRL = subR->_left;      // 右子树的左子树（失衡的关键节点）

		// 1. 先对右子树subR进行右旋
		RotateRight(subR);
		// 2. 再对失衡节点parent进行左旋
		RotateLeft(parent);
	}

注：这里的四个"旋转"详细情况请看《C++：AVL树》，在这里不做过多赘述。

cpp 复制代码

	// 递归校验红黑树的平衡性（核心辅助函数）
// 参数说明：
//   cur：当前遍历的节点
//   blackNum：引用参数，累计从根节点到当前路径的黑色节点数量
//   blackNumRef：参考值，即最左路径的黑色节点总数（用于校验所有路径黑色节点数是否相等）
// 返回值：true表示当前子树平衡，false表示不平衡
	bool Check(Node* cur, int& blackNum, const int blackNumRef) {
		// 1. 处理空节点（红黑树中，空节点视为黑色叶子节点）
		if (!cur) {
			// 校验：当前路径的黑色节点数必须与参考值相等
			if (blackNum != blackNumRef) {
				cout << "路径黑色节点数量不相等，红黑树不平衡" << endl;
				return false;
			}
			return true; // 空路径符合规则
		}

		// 2. 累计当前路径的黑色节点数（仅黑色节点计数）
		if (cur->_col == BLACK) {
			blackNum++; // 每遇到一个黑色节点，计数器+1
		}

		// 3. 校验红黑树核心规则：红色节点的父节点不能是红色（避免连续红节点）
		if (cur->_col == RED) {
			Node* parent = cur->_parent; // 获取父节点
			// 父节点存在且父节点为红色 → 违反规则
			if (parent && parent->_col == RED) {
				cout << "节点 " << cur->_kv.first << " 存在连续红色父节点，红黑树不平衡" << endl;
				return false;
			}
		}

		// 4. 递归校验左子树和右子树
		//   先校验左子树，若左子树不平衡则直接返回false
		//   左子树平衡后，再校验右子树，确保两侧都符合规则
		return Check(cur->_left, blackNum, blackNumRef) && Check(cur->_right, blackNum, blackNumRef);
	}

4.1 功能

用于递归验证红黑树是否满足所有平衡规则，是红黑树完整性校验的核心逻辑。

4.2 实现逻辑

参数说明 ：cur为当前遍历节点，blackNum为当前路径的黑色节点计数（引用传递），blackNumRef为参考黑色节点数（最左路径的黑节点数）。
空节点处理 ：若cur为空，检查当前路径黑节点数是否与blackNumRef相等，相等则符合规则，否则不平衡。
黑色节点计数 ：若当前节点为黑色，blackNum加1。
连续红节点检查：若当前节点为红色，检查其父节点是否也为红色，若是则存在连续红节点，树不平衡。
递归遍历：分别递归检查左子树和右子树，只有左右子树都满足规则时，树才平衡。

5.红黑树的递归工具函数（节点总数与高度计算）

cpp 复制代码

	// 计算节点总数的递归实现
	int _Size(Node* root)
	{
		return !root ? 0 : _Size(root->_left) + _Size(root->_right) + 1;
	}

	// 计算树高度的递归实现
	int _Height(Node* root)
	{
		if (!root){return 0;  }// 空树高度为0
		int leftHeight = _Height(root->_left);   // 左子树高度
		int rightHeight = _Height(root->_right); // 右子树高度
		return max(leftHeight, rightHeight) + 1; // 当前节点高度 = 左右子树最大高度 + 1
	}

5.1 函数功能与实现

_Size函数：
- 功能：计算红黑树的节点总数。
- 实现逻辑：采用递归方式，若当前节点root为空，返回0；否则返回左子树节点数（_Size(root->_left)）与右子树节点数（_Size(root->_right)）之和加1（当前节点）。
_Height函数：
- 功能：计算红黑树的高度。
- 实现逻辑：递归遍历，空树高度为0；否则当前节点高度为左子树高度（leftHeight）和右子树高度（rightHeight）的最大值加1。

cpp 复制代码

	// 中序遍历递归实现
	void _InOrder(Node* root)
	{
		if (!root)return;
		
		_InOrder(root->_left);         // 遍历左子树
		cout << root->_kv.first << ":" << root->_kv.second << endl;  // 访问当前节点
		_InOrder(root->_right);        // 遍历右子树
	}
	};

中序遍历的代码已在《C++：二叉平衡搜索树》《C++：AVL树》中出现，不在此赘述

6.测试代码

cpp 复制代码

#include <iostream>
#include <vector>
using namespace std;

// 引入红黑树定义（此处需包含上述红黑树完整代码）
// ...（上述红黑树的类和结构体定义）

int main() {
    // 测试1：基本插入与中序遍历（验证二叉搜索树特性）
    RBTree<int, int> rbt;
    vector<pair<int, int>> testData = {
        {10, 100}, {20, 200}, {5, 50}, {15, 150},
        {30, 300}, {40, 400}, {50, 500}, {35, 350}
    };

    cout << "=== 插入测试数据 ===" << endl;
    for (auto& kv : testData) {
        bool ret = rbt.Insert(kv);
        cout << "插入 " << kv.first << "：" << (ret ? "成功" : "失败（重复键）") << endl;
    }

    // 测试2：中序遍历（应按键升序输出，验证二叉搜索树有序性）
    cout << "\n=== 中序遍历结果（升序） ===" << endl;
    rbt.InOrder();

    // 测试3：查找功能
    cout << "\n=== 查找测试 ===" << endl;
    vector<int> findKeys = {15, 30, 100};
    for (int key : findKeys) {
        auto node = rbt.Find(key);
        if (node) {
            cout << "找到键 " << key << "，值为 " << node->_kv.second << endl;
        } else {
            cout << "未找到键 " << key << endl;
        }
    }

    // 测试4：平衡性检查（验证红黑树规则）
    cout << "\n=== 平衡性检查 ===" << endl;
    bool isBalanced = rbt.IsBalanceTree();
    cout << "红黑树" << (isBalanced ? "符合" : "不符合") << "所有平衡规则" << endl;

    // 测试5：节点总数与高度
    cout << "\n=== 树结构信息 ===" << endl;
    cout << "节点总数：" << rbt.Size() << endl;
    cout << "树的高度：" << rbt.Height() << endl;

    // 测试6：插入重复键
    cout << "\n=== 插入重复键测试 ===" << endl;
    bool ret = rbt.Insert({10, 1000}); // 10已存在
    cout << "插入重复键10：" << (ret ? "成功（错误）" : "失败（正确）") << endl;

    return 0;
}

以下是针对上述红黑树实现的测试代码，用于验证插入、查找、平衡性检查等功能的正确性：

cpp 复制代码

#include"RBTree.h"//已包含红黑树的模拟实现的所有代码
#include <iostream>
#include <vector>
using namespace std;


int main() {
    // 测试1：基本插入与中序遍历（验证二叉搜索树特性）
    RBTree<int, int> rbt;
    vector<pair<int, int>> testData = {
        {10, 100}, {20, 200}, {5, 50}, {15, 150},
        {30, 300}, {40, 400}, {50, 500}, {35, 350}
    };

    cout << "=== 插入测试数据 ===" << endl;
    for (auto& kv : testData) {
        bool ret = rbt.Insert(kv);
        cout << "插入 " << kv.first << "：" << (ret ? "成功" : "失败（重复键）") << endl;
    }

    // 测试2：中序遍历（应按键升序输出，验证二叉搜索树有序性）
    cout << "\n=== 中序遍历结果（升序） ===" << endl;
    rbt.InOrder();

    // 测试3：查找功能
    cout << "\n=== 查找测试 ===" << endl;
    vector<int> findKeys = {15, 30, 100};
    for (int key : findKeys) {
        auto node = rbt.Find(key);
        if (node) {
            cout << "找到键 " << key << "，值为 " << node->_kv.second << endl;
        } else {
            cout << "未找到键 " << key << endl;
        }
    }

    // 测试4：平衡性检查（验证红黑树规则）
    cout << "\n=== 平衡性检查 ===" << endl;
    bool isBalanced = rbt.IsBalanceTree();
    cout << "红黑树" << (isBalanced ? "符合" : "不符合") << "所有平衡规则" << endl;

    // 测试5：节点总数与高度
    cout << "\n=== 树结构信息 ===" << endl;
    cout << "节点总数：" << rbt.Size() << endl;
    cout << "树的高度：" << rbt.Height() << endl;

    // 测试6：插入重复键
    cout << "\n=== 插入重复键测试 ===" << endl;
    bool ret = rbt.Insert({10, 1000}); // 10已存在
    cout << "插入重复键10：" << (ret ? "成功（错误）" : "失败（正确）") << endl;

    return 0;
}

测试说明：

插入功能：通过多组数据测试插入逻辑，包括重复键的处理（应插入失败）。
中序遍历：验证红黑树的二叉搜索树特性（中序遍历结果为键的升序）。
查找功能：测试存在的键和不存在的键，验证查找结果的正确性。
平衡性检查 ：通过IsBalanceTree函数验证插入后是否仍满足红黑树规则（根为黑、无连续红节点、各路径黑节点数相等）。
结构信息 ：通过Size和Height函数查看树的规模和高度，辅助验证近似平衡性（高度应接近2*log2(n)）。

预期结果：

插入非重复键均成功，重复键失败。
中序遍历按键升序输出（5,10,15,20,30,35,40,50）。
查找存在的键（15,30）返回对应节点，查找不存在的键（100）返回空。
平衡性检查输出"符合所有平衡规则"。
节点总数为8，高度约为4~5（符合红黑树近似平衡特性）。

红黑树

一.初识红黑树

1.红黑树的概念

2.红黑树的核心规则

3.说明

4.红黑树的效率分析

二.红黑树的简单模拟实现

1.红黑树节点结构

代码解释

2.红黑树的插入

（1）空树处理

（2）二叉搜索树插入逻辑

（3）插入后平衡调整（核心）

场景1：父节点是祖父节点的左孩子（grandfather->_left == parent）

子场景1.1：叔叔存在且为红色（uncle && uncle->_col == RED）

子场景1.2：叔叔不存在或为黑色（!uncle || uncle->_col == BLACK）

场景2：父节点是祖父节点的右孩子（grandfather->_right == parent）

（4）最终保证根节点为黑色

总结

2.红黑树的查找

2.1 功能

2.2 实现逻辑

3.检查红黑树是否平衡

3.1 功能

3.2 实现逻辑

4. 红黑树的基础操作封装（节点总数、高度与中序遍历）

4.1 功能

4.2 实现逻辑

5.红黑树的递归工具函数（节点总数与高度计算）

5.1 函数功能与实现

6.测试代码

测试说明：

预期结果：

场景1：父节点是祖父节点的左孩子（`grandfather->_left == parent`）

子场景1.1：叔叔存在且为红色（`uncle && uncle->_col == RED`）

子场景1.2：叔叔不存在或为黑色（`!uncle || uncle->_col == BLACK`）

场景2：父节点是祖父节点的右孩子（`grandfather->_right == parent`）