问题
给定 n 个非负整数表示海拔高度,其中每个条形的宽度为 1 ,计算下雨后可以接多少水。
例1:
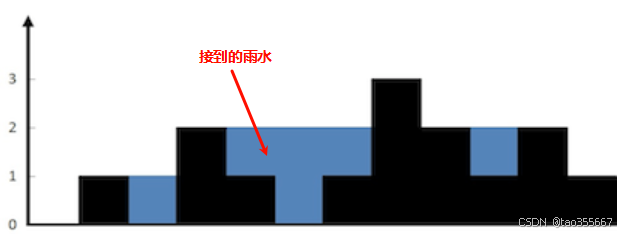
Input: height = [0,1,0,2,1,0,1,3,2,1,2,1]
Output: 6
Explanation: 上述海拔图(黑色部分)由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示。在这种情况下,共可储存 6 个单位的雨水(蓝色部分)。
例2:
Input: height = [4,2,0,3,2,5]
Output: 9
约束:
n == height.length1 <= n <= 2 * 1040 <= height[i] <= 105
解1:暴力
我们只需计算每个"黑色条形"上方可以累积多少"雨水",之后求和,就得到了最终的雨水数量。
- 对最左和最右的"黑色条形",显然不会累积雨水
- 对中间的"黑色条形",记其海拔为
m,当其两侧均存在比它高的海拔,才有可能累积雨水- 找到其左侧比它高的最高海拔记为
l,右侧比它高的最高海拔记为r,则m上方累积的雨水数量为 m i n ( l , r ) − m min(l,r)-m min(l,r)−m
- 找到其左侧比它高的最高海拔记为
时间复杂度 O ( n 2 ) O(n^2) O(n2):对中间的每个海拔,都要遍历一次两侧的海拔,时间复杂度为 O ( ( n − 2 ) ∗ ( n − 1 ) ) = O ( n 2 ) O((n-2)*(n-1))=O(n^2) O((n−2)∗(n−1))=O(n2)
空间复杂度 O ( 1 ) O(1) O(1):随着问题规模n的增大, 需要的额外空间不变
python
class Solution:
def trap(self, height: List[int]) -> int:
n = len(height)
ans = 0
for i in range(n):
lh = 0 # left height
rh = 0 # right height
for l in range(0, i):
lh = max(lh, height[l])
for r in range(i + 1, n):
rh = max(rh, height[r])
if lh > height[i] and rh > height[i]:
ans += min(lh, rh) - height[i]
return ans超时了,但能过319个用例,说明思路没问题

解2:动态规划,左右遍历,空间换时间
还是接着刚才的思路,通过遍历解决问题,但是这次采用两次遍历,一次正向,一次反向,从而得到需要的最大海拔。
- 正向遍历:用数组
lh记录对应下标左侧的最大海拔。如lh[2]记录了height[0],height[1],height[2]中的最大值。 - 反向遍历:用数组
rh记录对应下标右边侧的最大海拔。如lh[2]记录了height[2],height[3],height[4]中的最大值(总长度为5)。 - 之后用
lh和rh计算每个海拔头上的雨水,求和
时间复杂度 O ( n ) O(n) O(n):需要遍历2次数组,还要遍历一次lh和rh,时间复杂度为 O ( 4 n ) = O ( n ) O(4n)=O(n) O(4n)=O(n)
空间复杂度 O ( n ) O(n) O(n):需要用数组lh和rh存储中间结果
python
class Solution:
def trap(self, height: List[int]) -> int:
n = len(height)
ans = 0
lh = [0] * n # left height
rh = [0] * n # right height
now_max=0
for i in range(n):
now_max=max(now_max,height[i])
lh[i]=now_max
now_max=0
for i in range(n-1,-1,-1):
now_max=max(now_max,height[i])
rh[i]=now_max
for i in range(1,n-1):
if lh[i-1]>height[i] and rh[i+1]>height[i]:
# print(f"rain{i}={min(lh[i-1],rh[i+1])-height[i]}")
ans += min(lh[i-1],rh[i+1])-height[i]
return ans过了
解3:单调栈
解4:双指针
补充
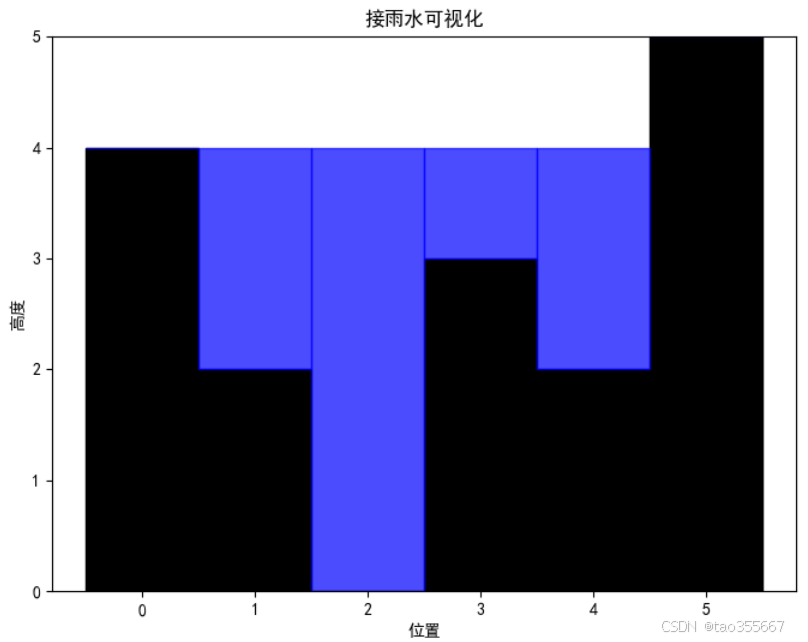
接雨水可视化
python
import matplotlib.pyplot as plt
import numpy as np
# 设置中文显示
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False # 解决负号显示问题
def trap_rain_water_visualization(height):
n = len(height)
if n == 0:
return
# 计算左右最大高度数组
left_max = [0] * n
right_max = [0] * n
left_max[0] = height[0]
for i in range(1, n):
left_max[i] = max(left_max[i-1], height[i])
right_max[-1] = height[-1]
for i in range(n-2, -1, -1):
right_max[i] = max(right_max[i+1], height[i])
# 计算每个位置的雨水量
water = [max(0, min(left_max[i], right_max[i]) - height[i]) for i in range(n)]
# 绘图
x = np.arange(n)
fig, ax = plt.subplots(figsize=(8, 6))
# 绘制柱子(黑色表示原高度)
ax.bar(x, height, width=1, color='black', edgecolor='black')
# 绘制雨水(蓝色表示雨水)
ax.bar(x, water, width=1, bottom=height, color='blue', alpha=0.7, edgecolor='blue')
# 设置标题和标签
ax.set_title('接雨水可视化')
ax.set_xlabel('位置')
ax.set_ylabel('高度')
ax.set_xticks(x)
ax.set_xticklabels(x)
plt.grid(False)
plt.show()
# 测试数组
height = [4, 2, 0, 3, 2, 5]
trap_rain_water_visualization(height)