在了解kruskal算法之前我们先了解一下并查集的一些概念,并查集会有一些可以优化的方法,这里我们只是简单说明不进行详细解释
并查集
核心思想与存储
并查集通常使用一个数组(或字典)来实现。我们称这个数组为 parent。
-
每个元素都对应数组中的一个位置。
-
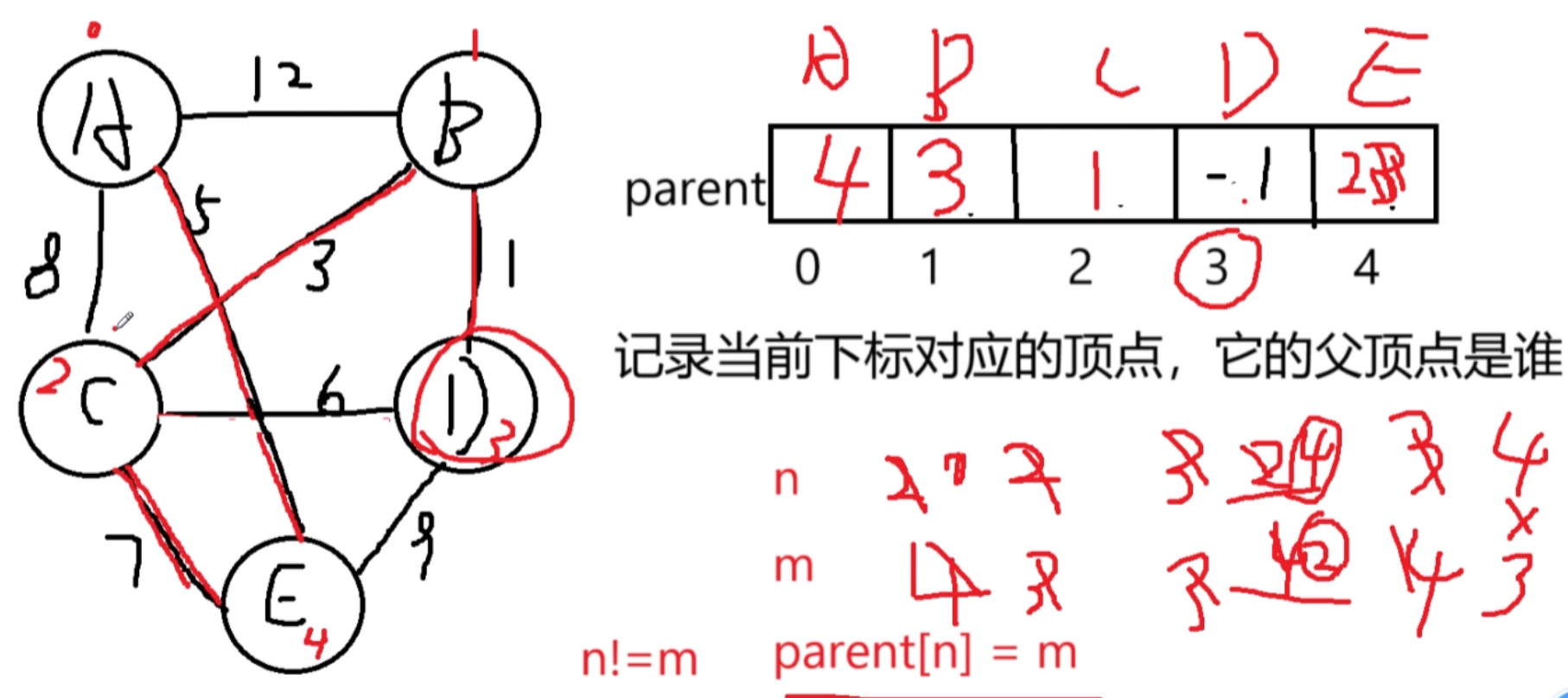
parent[i]表示元素i的"父节点"。 -
如果
parent[i] == i,那么i就是这个集合的根节点。根节点是整个集合的代表。
初始化:一开始,每个元素各自构成一个集合。即 parent[i] = i。
查找
功能:找到元素 i 所在集合的根节点。
朴素实现:不断向上寻找父节点,直到找到根节点(parent[i] == i)。
问题:如果树变得很高,查找效率会很低,最坏情况是 O(n)。
优化:路径压缩
合并
功能:将两个元素所在的集合合并成一个集合。
朴素实现:找到两个元素的根节点 rootA 和 rootB,然后将其中一个根节点的父节点设置为另一个根节点。
问题:随意合并可能导致树的高度增长过快,甚至退化成一条链。
优化:按秩合并
qsort函数
函数原型:
cpp
#include <stdlib.h>
void qsort(void *base, size_t nmemb, size_t size,
int (*compar)(const void *, const void *));参数说明
-
base: 指向数组第一个元素的指针 -
nmemb: 数组中元素的个数 -
size: 每个元素的大小(字节数) -
compar: 比较函数指针
比较函数
比较函数必须遵循以下格式:
cpp
int compar(const void *a, const void *b);返回值:
-
< 0: a 在 b 前面
-
= 0: a 和 b 相等
-
> 0: a 在 b 后面
Kruskal算法及代码
Kruskal算法的思想非常直观,可以概括为"从小到大挑边,只要不形成环就入选"。
那么我们先定义包含一个边的权重和两个顶点的结构体(一条边包含2个顶点):
cpp
typedef struct asc{
int v1;//顶点e1下标v1;
int v2;//顶点e2下标v2;
int weight;//权重
}Asc;创建边的结构体数组 : Arc* arcs = malloc(sizeof(Arc)*g->edgeNum);并对其进行初始化;
由于使用的是邻接矩阵,所以两层for循环进行遍历,由于图是无向图,所以这里下标i->j和下标j->i的权值相同,所以只需要遍历i->j的方向即可,也就是邻接矩阵的右上角所有权值;
cpp
//创建边集的数组
Arc* arcs = malloc(sizeof(Arc)*g->edgeNum);
int k = 0;
//邻接矩阵g->edge[i][j]表示:顶点下标为i的元素到下标为j的元素,顶点i、j之间边权值;
for(int i = 0;i < g->edgeNum;i++){
//无向图:i->j有值,那么j->i也有值,所以我们下标从小到大
for(int j = i + 1;j < g->edgeNum;j++){
if(g->edge[i][j]!=INT_MAX){//说明i->j有值
arcs[k].v1 = i;
arcs[k].v2 = j;
arcs[k].weight = g->edge[i][j];//最后边要按照weight排序
k++;
}
}
}//将所有边利用新结构Arc进行初始化添加完所有边以后,利用qsort函数对这些边进行排序(最后一行代码):
cpp
//创建边集的数组
Arc* arcs = malloc(sizeof(Arc)*g->edgeNum);
int k = 0;
//邻接矩阵g->edge[i][j]表示:顶点下标为i的元素到下标为j的元素,顶点i、j之间边权值;
for(int i = 0;i < g->edgeNum;i++){
//无向图:i->j有值,那么j->i也有值,所以我们下标从小到大
for(int j = i + 1;j < g->edgeNum;j++){
if(g->edge[i][j]!=INT_MAX){//说明i->j有值
arcs[k].v1 = i;
arcs[k].v2 = j;
arcs[k].weight = g->edge[i][j];//最后边要按照weight排序
k++;
}
}
}//将所有边利用新结构Arc进行初始化
int *parent = malloc(sizeof(int)*g->vertexNum);
for(int i = 0;i < g->vertexNum;i++){
parent[i] = -1;
//或者parent[i] = i;
}
//先将边按权重排序;
//使用库函数qsort回调函数
qsort(arcs,g->edgeNum,sizeof(arcs[0]),compare);//将边按权重排序;Compare是自定义比较函数:
cpp
int compare(void const *e1,void const *e2){
Arc* p1 = (Arc*)e1;
Arc* p2 = (Arc*)e2;
return p1->weight - p2->weight;
}//qsort比较,返回的值是小于0,不进行交换已知Kruskal每次连接时,都是进行最小生成树的合并,并且不构成回路,我们先定义一个parent数组,用来存放每个顶点的父节点,一开始,我们令他们的根节点值全部为-1,或者全部为他们本身:parent[i] = -1或者i;作为判断是否是根节点的判断条件;
cpp
int* parent = malloc(sizeof(int)*g->vertexNum);
for(int i = 0; i < vertexNum;i++){
parent[i] = -1;
}然后进行从下标0开始将所有的边集数组进行遍历,因为边集数组已经使用qsort函数进行排序,每次选择第i个边,判断这条边的顶点是否和已选边是同一顶点的下标,如果是,就不选这条边,继续i++,判断新的边元素和已选边是否是同一父节点;
cpp
for(int i = 0;i < g->edgeNum;i++){
//执行边的个数次,因为会有环,所以要将所有边都遍历;
//找边对应的两个顶点的父顶点下标;
int n = find(parent,arcs[i].v1);//顶点v1的父亲节点下标
int m = find(parent,arcs[i].v2);
if(n!=m){
parent[n] = m;
printf("%c %c ->%d\n",g->v[arcs[i].v1],
g->v[arcs[i].v2],arcs[i].weight);
}
}如果不是同一棵子树(两个子树的根节点的下标不相同),就让一棵子树的根节点连接到另一棵子树的根节点上,实现两颗棵子树的合并,当for循环结束时,最小生成树生成结束。
大致代码:
cpp
typedef struct Arc
{
int v1;
int v2;
int weight;
}Arc;
int compare(void const* e1, void const* e2)
{
Arc* p1 = (Arc*)e1;
Arc* p2 = (Arc*)e2;
return p1->weight - p2->weight;
}
int find(int* parent, int v)
{
while (parent[v] > 0)
{
v = parent[v];
}
return v;
}
void miniSpanTree_Kruskal(Graph* g)
{
//创建边集数组
Arc* arcs = malloc(sizeof(Arc) * g->edgeNum);
//初始化这个数组
int k = 0;
for (int i = 0; i < g->vertexNum; i++)
{
for (int j = i + 1; j < g->vertexNum; j++)
{
if (g->edge[i][j] != INT_MAX)
{
arcs[k].v1 = i;
arcs[k].v2 = j;
arcs[k].weight = g->edge[i][j];
k++;
}
}
}
int* parent = malloc(sizeof(int) * g->vertexNum);
for (int i = 0; i < g->vertexNum; i++)
{
parent[i] = -1;
}
qsort(arcs, g->edgeNum,sizeof(arcs[0]),compare);
for (int i = 0; i < g->edgeNum; i++)
{
//找出这条边依附的两个顶点的父顶点下标
int n = find(parent, arcs[i].v1);
int m = find(parent, arcs[i].v2);
if (n != m)
{
parent[n] = m;
printf("(%c,%c)=>%d\n",
g->v[arcs[i].v1], g->v[arcs[i].v2], arcs[i].weight);
}
}
}完整代码请看:hjh0127/gitee中的graph_Kruskal.c文件,里面也有上一篇文章中的Prim算法。