[人工智能-大模型-107]：模型层 - 神经元的功能角色：特征提取与相似度量化

本文结合数学抽象与实际功能，从数学原理、功能角色、拟合与映射的深层关系三个维度进一步展开，并补充直观类比与实际应用场景。

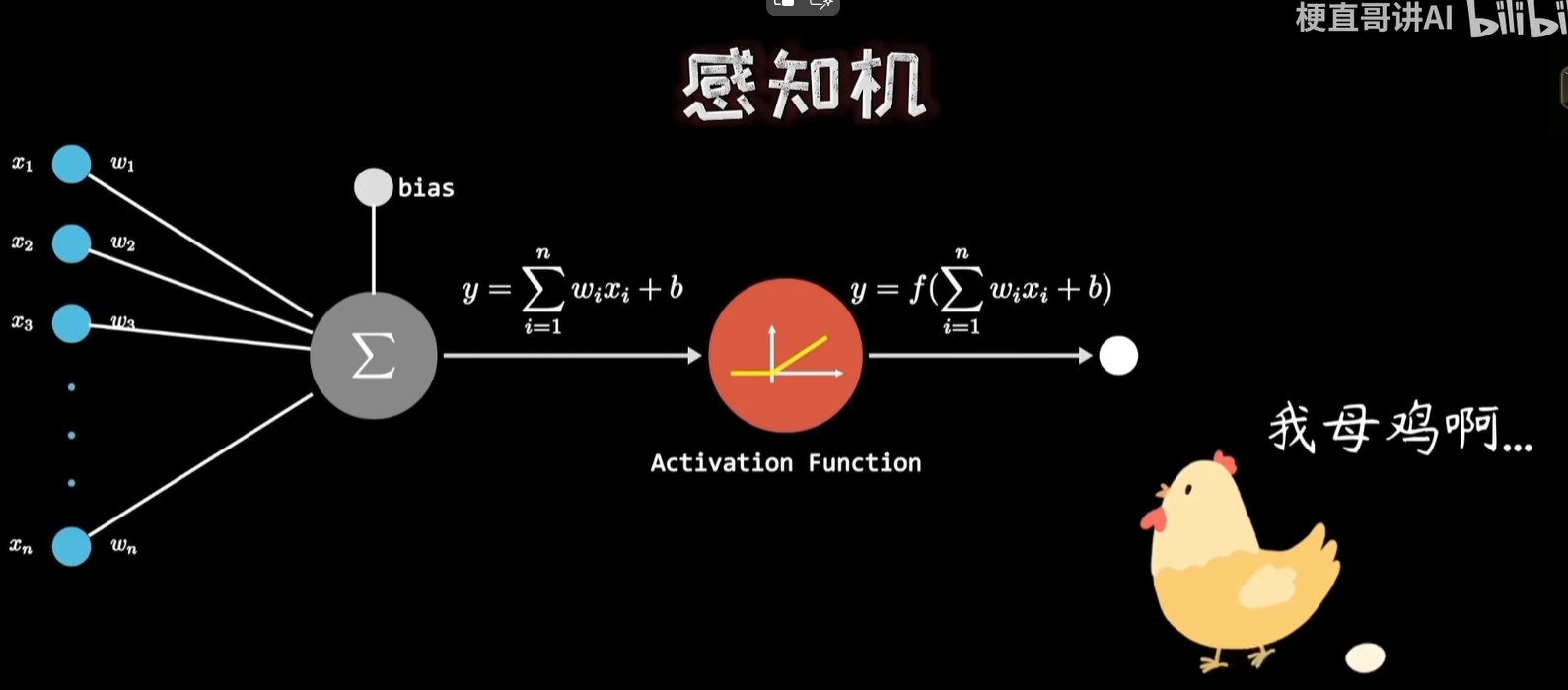
一、神经元的数学本质：加权求和与激活的复合函数

特征提取 ：
- 权重 w 通过训练自动学习，使得神经元对输入中的特定模式敏感。例如：
  - 在图像识别中，某个神经元可能对"水平边缘"特征响应强烈；
  - 在自然语言处理中，另一个神经元可能对"否定词+情感词"的组合敏感。
- 偏置 b 调整神经元的"激活阈值"，控制对弱信号的容忍度。
相似度量化 ：
- 输出值 a 的大小直接反映输入与期望特征的匹配程度：
  - Sigmoid/Softmax：输出值在 $0,1$ 区间，可解释为概率或置信度；
  - ReLU：输出值≥0，数值越大表示匹配越强（负值被截断为0，表示不相关）。
- 示例：
  若训练一个手写数字识别神经元检测"圆圈"特征，当输入图像包含明显圆圈时，该神经元的输出值会显著高于其他神经元。

拟合函数 ：
- 神经元通过调整权重 w 和偏置 b，拟合输入-输出之间的复杂关系。
- 线性可分情况：单个神经元可拟合线性决策边界（如感知机）；
- 非线性情况：通过堆叠多层神经元（如深度网络），可拟合任意复杂函数（依据通用近似定理）。
- 优化目标：最小化损失函数（如交叉熵损失），使神经元输出逼近期望值。
映射函数 ：
- 神经元将输入数据从原始N维空间映射到标量空间（即输出值 a）。
- 几何意义 ：权重向量 w 定义了一个超平面，输入数据在超平面上的投影距离（通过点积计算）决定了输出值的大小。
- 多神经元协作 ：多个神经元共同构成一个基，将输入数据映射到更高维的特征空间（如隐藏层的作用）。

直观图示 ：

假设输入是二维数据（x1,x2），权重 w=(w1,w2) 定义了一条直线。点积 z=w1x1+w2x2 计算输入点到直线的有向距离，激活函数则根据距离大小输出匹配度。

图像分类 ：
- 底层神经元检测边缘、纹理等低级特征；
- 高层神经元组合低级特征，检测"车轮""面部"等高级概念；
- 输出层神经元量化图像属于各类别的概率。
语音识别 ：
- 神经元检测音素、语调等声学特征；
- 通过时序建模（如RNN）捕捉语音的上下文依赖。
推荐系统 ：
- 神经元对用户历史行为（如点击、购买）和物品属性（如类别、价格）进行特征交叉；
- 输出值预测用户对物品的偏好程度。

维度	描述
数学形式	线性变换 + 非线性激活，构成复合函数 a=σ(wTx+b)
功能目标	从输入中提取特定特征，量化其与期望模式的匹配度
权重作用	拟合输入-输出关系，定义特征检测的方向与阈值
输出意义	数值大小反映特征相似度，激活函数决定响应的敏感性与范围

神经元的简洁性（仅需权重、偏置和激活函数）与其强大的表达能力（可堆叠为深度网络）形成了鲜明对比，这正是神经网络成功的关键。理解神经元的本质，有助于设计更高效的模型结构（如注意力机制中的动态权重调整）或解释模型行为（如通过特征可视化）。