深入理解二叉搜索树：从原理到实现

我星期八休息2025-10-31 13:00

目录

[一、 二叉搜索树的概念与特性](#一、 二叉搜索树的概念与特性)

[二、 二叉搜索树的性能分析](#二、 二叉搜索树的性能分析)

三、二叉搜索树的核心操作

[3.1 插入操作](#3.1 插入操作)

[3.2 查找操作](#3.2 查找操作)

[3.3 删除操作](#3.3 删除操作)

四、二叉搜索树的完整实现

[4.1 基础版本（Key模型）](#4.1 基础版本（Key模型）)

[4.2 扩展版本（Key-Value模型）](#4.2 扩展版本（Key-Value模型）)

五、二叉搜索树的应用场景

[5.1 key搜索场景](#5.1 key搜索场景)

[5.2 Key-Value模型应用场景](#5.2 Key-Value模型应用场景)

六、总结

本文将详细解析二叉搜索树的核心概念、操作实现及应用场景，帮助读者全面掌握这一重要的数据结构。

一、 二叉搜索树的概念与特性

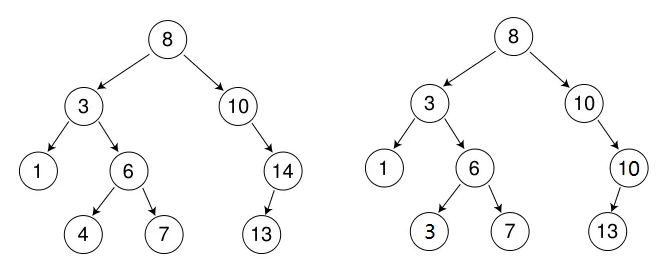
二叉搜索树（Binary Search Tree，BST），又称二叉排序树，是一种特殊的二叉树数据结构，它具有以下性质：

  • 若左子树非空，则左子树上所有节点的值都小于等于根节点的值

  • 若右子树非空，则右子树上所有节点的值都大于等于根节点的值

  • 左右子树也分别为二叉搜索树

重要说明：关于相等值的处理，二叉搜索树可以设计为支持或不支持重复值，这取决于具体应用场景。在C++ STL中：

  • map/set：不支持重复键值

  • multimap/multiset：支持重复键值

二、 二叉搜索树的性能分析

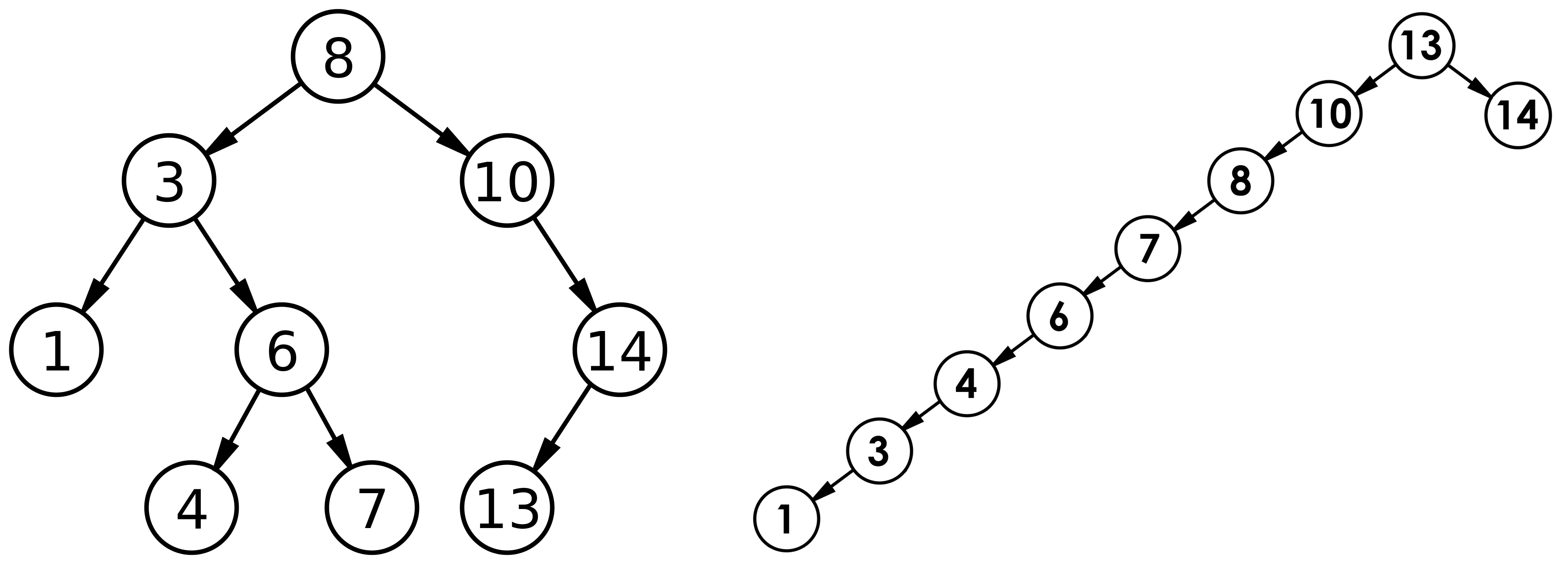
最优情况下，二叉搜索树为完全二叉树（或者接近完全二叉树），其高度为：log₂N

最差情况下，二叉搜索树退化为单支树(或者类似单支树)，其高度为：N

所以综合而言，二叉搜索树增删查改时间复杂度为：O(N)

那么这样的效率显然是无法满足我们需求的，我们后续课程需要继续讲解二叉搜索树的变形，平衡二叉树。二叉搜索树、AVL树和红黑树，才能适用于我们在内存中存储和搜索数据。

另外需要说明的是，二分查找也可以实现O(log₂N)级别的查找效率，但是二分查找有两大缺陷：

  1. 需要存储在支持下标随机访问的结构中，并且有序。

  2. 插入和删除数据效率很低，因为存储在支持下标随机访问的结构中，插入和删除数据一般需要挪动数据。

情况 树形态 树高度 操作时间复杂度
最优 完全二叉树 O(log₂N) O(log₂N)
最差 单支树 O(N) O(N)

三、二叉搜索树的核心操作

3.1 插入操作

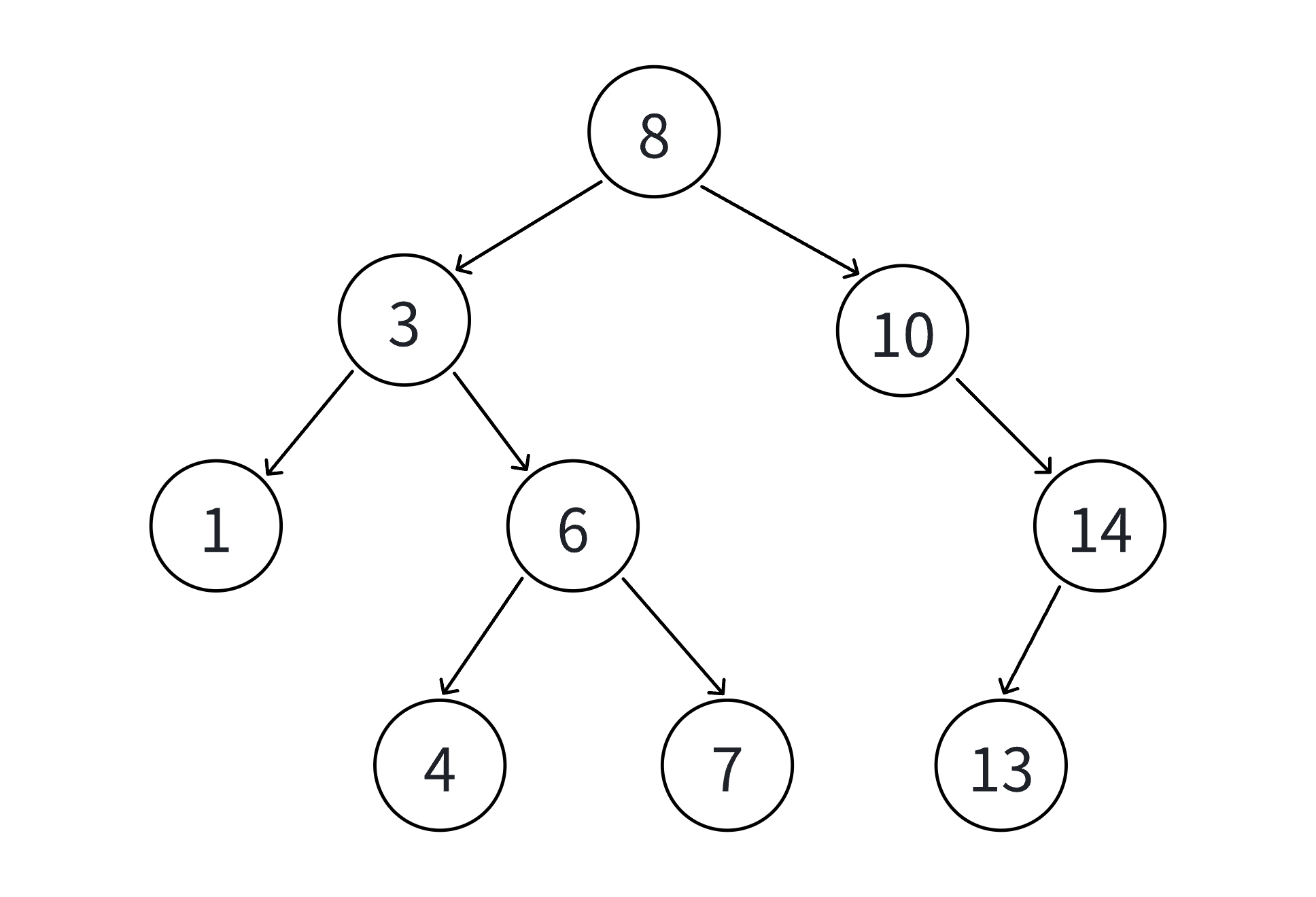
如下：

  1. 树为空，创建新节点作为根节点

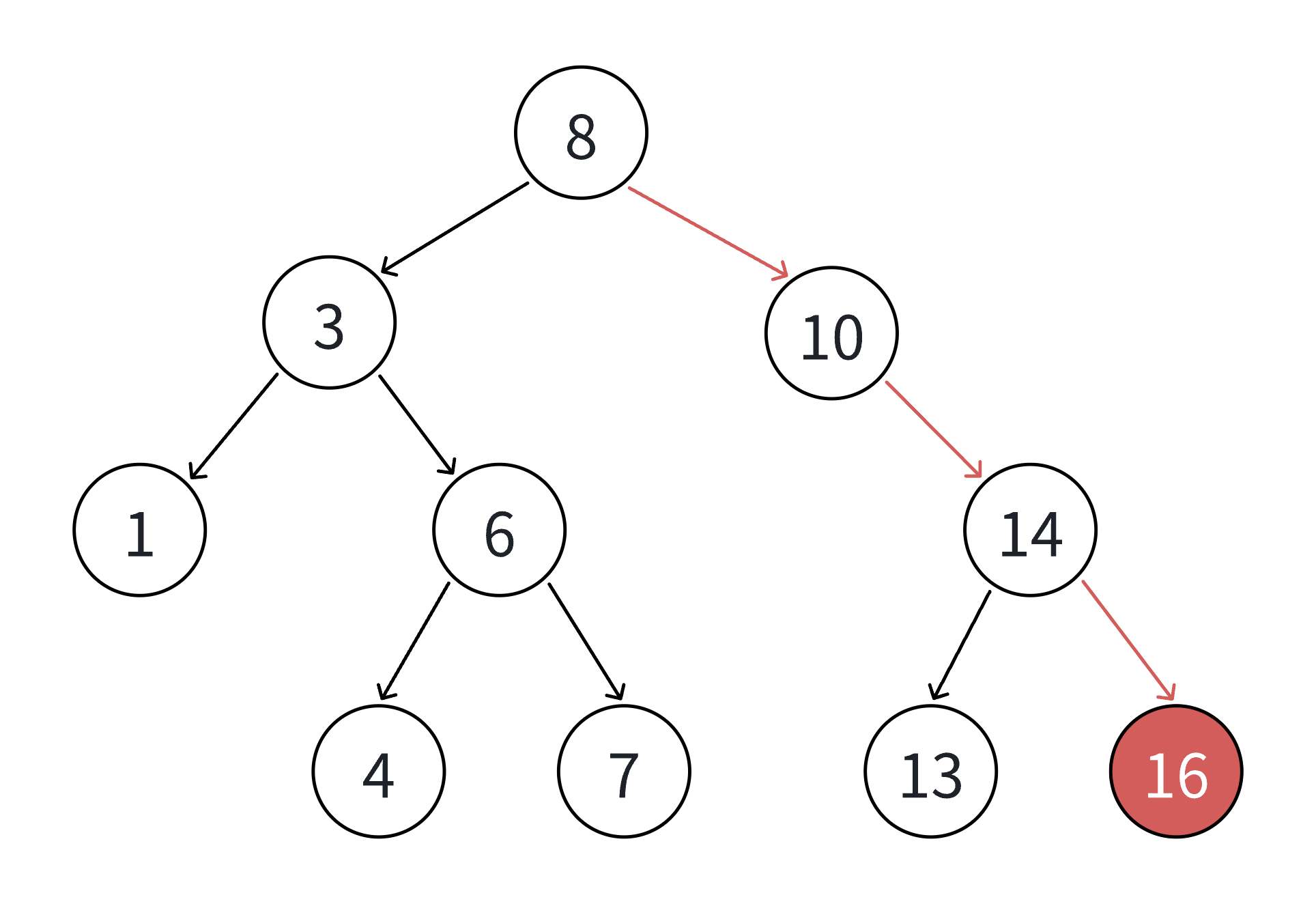
  2. 树非空，从根节点开始比较：

  • 插入值 > 当前节点值：向右子树移动

  • 插入值 < 当前节点值：向左子树移动

  • 插入值 = 当前节点值：根据设计决定（支持重复值则继续移动，否则返回失败）

  1. 找到空位置后插入新节点

代码实现：

cpp 复制代码 
bool Insert(const K& key) {
    if (_root == nullptr) {
        _root = new Node(key);
        return true;
    }

    Node* parent = nullptr;
    Node* cur = _root;
    while (cur) {
        if (cur->_key < key) {
            parent = cur;
            cur = cur->_right;
        } else if (cur->_key > key) {
            parent = cur;
            cur = cur->_left;
        } else {
            return false; // 不支持重复值
        }
    }
    
    cur = new Node(key);
    if (parent->_key < key) {
        parent->_right = cur;
    } else {
        parent->_left = cur;
    }
    return true;
}

3.2 查找操作

步骤：

  1. 从根节点开始比较

  2. 查找值 > 当前节点值：向右子树查找

  3. 查找值 < 当前节点值：向左子树查找

  4. 查找值 = 当前节点值：找到目标

  5. 遇到空节点：查找失败

代码实现：

cpp 复制代码 
bool Find(const K& key) {
    Node* cur = _root;
    while (cur) {
        if (cur->_key < key) {
            cur = cur->_right;
        } else if (cur->_key > key) {
            cur = cur->_left;
        } else {
            return true;
        }
    }
    return false;
}

3.3 删除操作

首先查找元素是否在二叉搜索树中，如果不存在，则返回false。

如果查找元素存在则分以下四种情况分别处理：（假设要删除的结点为N）

情况1：删除叶子节点

直接删除，父节点对应指针置空

情况2：删除只有右子树的节点

用右子树替代被删节点

情况3：删除只有左子树的节点

用左子树替代被删节点

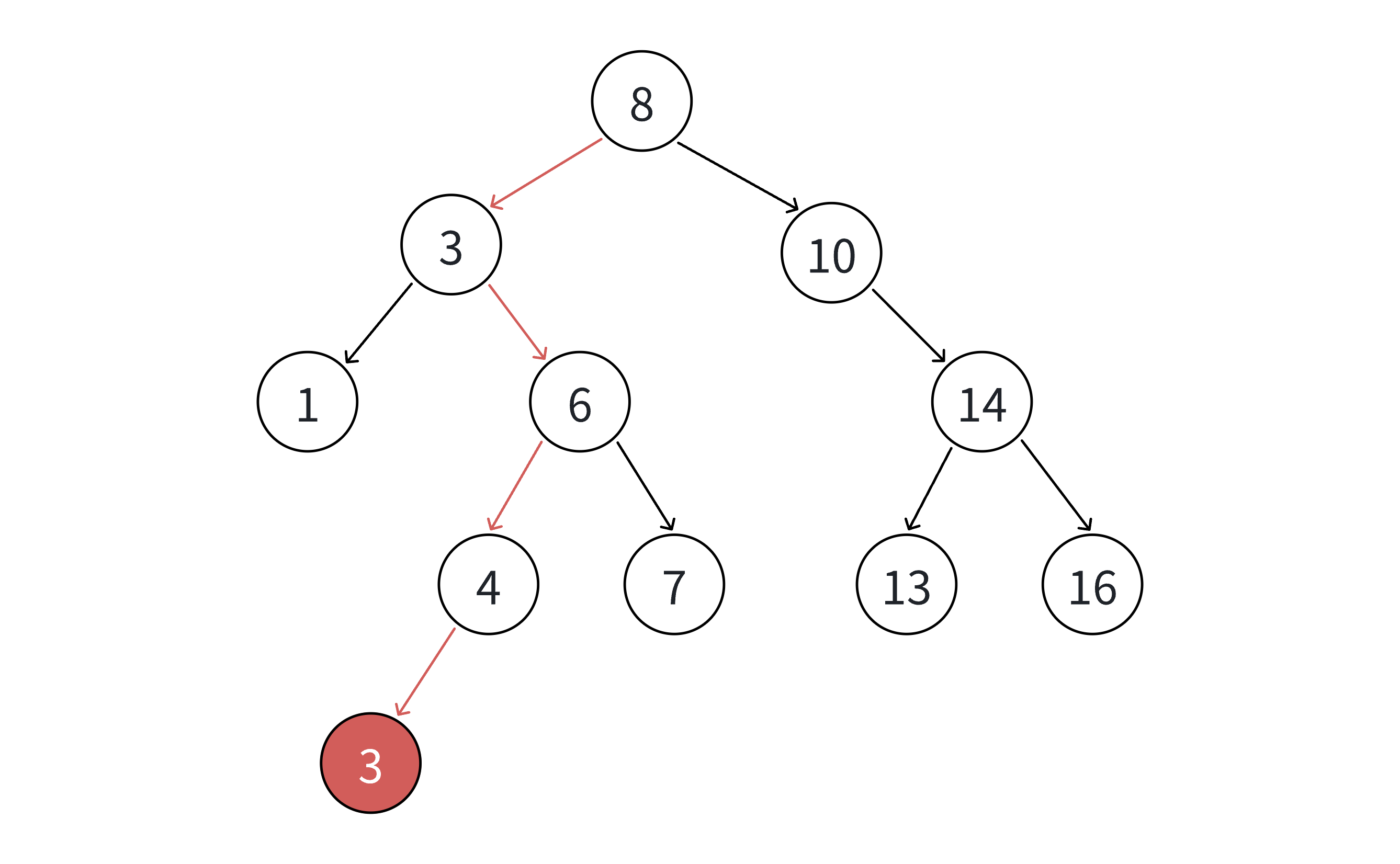
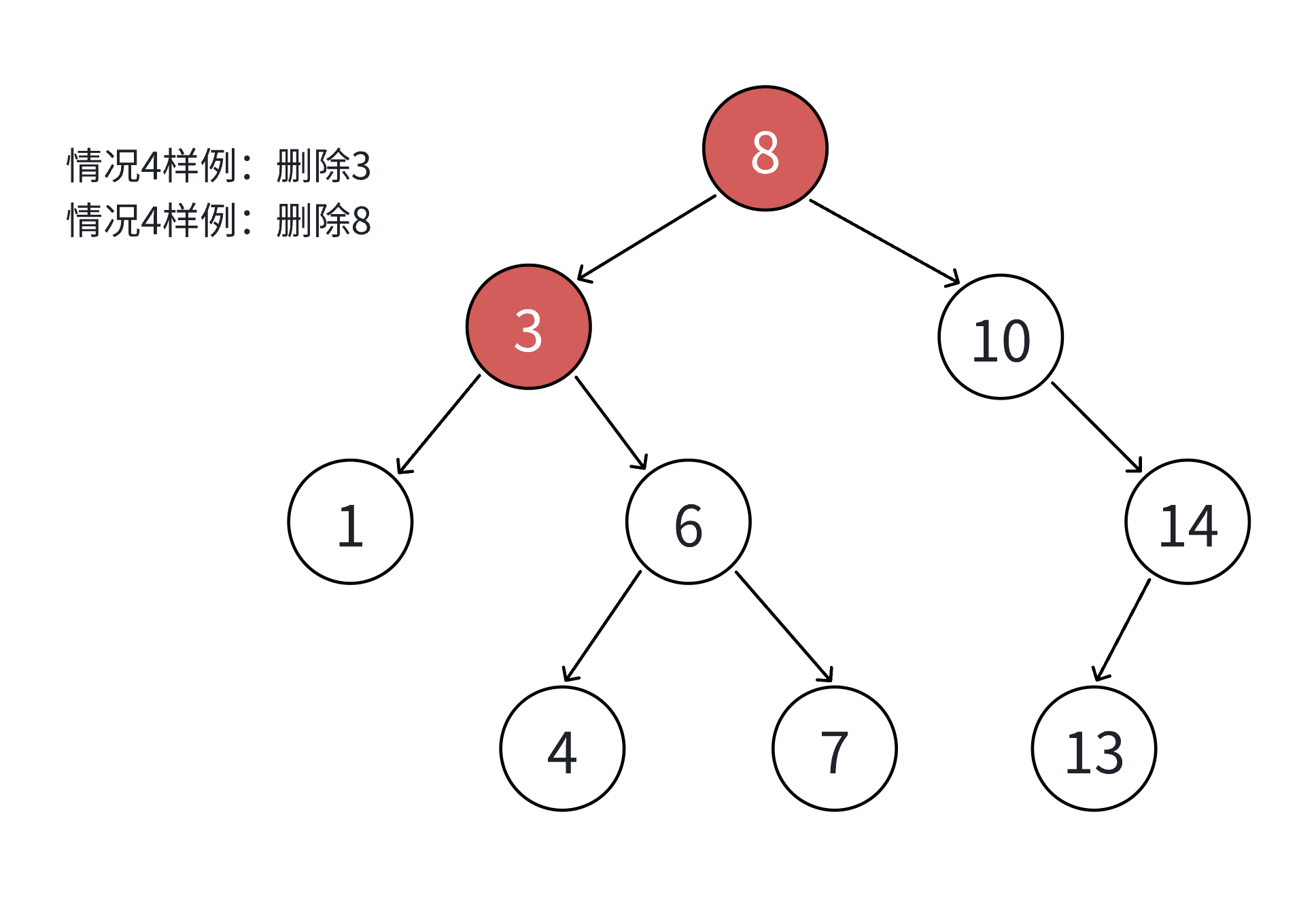
情况4：删除有两个子树的节点（最复杂）

使用替换法删除：

  • 找到左子树的最大节点或右子树的最小节点

  • 用找到的节点值替换待删除节点的值

  • 删除被替换的节点（该节点必定是情况1、2或3）

代码实现：

cpp 复制代码 
bool Erase(const K& key) {
    Node* parent = nullptr;
    Node* cur = _root;
    while (cur) {
        if (cur->_key < key) {
            parent = cur;
            cur = cur->_right;
        } else if (cur->_key > key) {
            parent = cur;
            cur = cur->_left;
        } else {
            // 找到要删除的节点
            if (cur->_left == nullptr) {
                // 情况1、2：无左子树
                if (parent == nullptr) {
                    _root = cur->_right;
                } else {
                    if (parent->_left == cur)
                        parent->_left = cur->_right;
                    else
                        parent->_right = cur->_right;
                }
                delete cur;
            } else if (cur->_right == nullptr) {
                // 情况3：无右子树
                if (parent == nullptr) {
                    _root = cur->_left;
                } else {
                    if (parent->_left == cur)
                        parent->_left = cur->_left;
                    else
                        parent->_right = cur->_left;
                }
                delete cur;
            } else {
                // 情况4：有两个子树
                // 找右子树的最小节点
                Node* rightMinParent = cur;
                Node* rightMin = cur->_right;
                while (rightMin->_left) {
                    rightMinParent = rightMin;
                    rightMin = rightMin->_left;
                }
                
                // 替换值
                cur->_key = rightMin->_key;
                
                // 删除右子树的最小节点
                if (rightMinParent->_left == rightMin)
                    rightMinParent->_left = rightMin->_right;
                else
                    rightMinParent->_right = rightMin->_right;
                    
                delete rightMin;
            }
            return true;
        }
    }
    return false;
}

四、二叉搜索树的完整实现

4.1 基础版本（Key模型）

Key模型 是最基础的版本控制方式，主要用于管理简单的键值对数据。它的核心特点包括：

1. 数据结构

  • 采用最简单的键值对存储方式

  • 每个Key对应一个Value

  • Value可以是字符串、数字等基本数据类型

2. 版本控制机制

  • 每次修改都会生成新的版本记录

  • 通过时间戳或版本号标识不同版本

  • 支持基本的版本回退功能

3. 典型应用场景

  • 配置管理：如保存应用的参数配置

  • 用户偏好设置：存储用户的自定义设置

  • 简单的元数据管理：如产品属性、标签等

cpp 复制代码 
template<class K>
struct BSTNode {
    K _key;
    BSTNode<K>* _left;
    BSTNode<K>* _right;

    BSTNode(const K& key)
        : _key(key), _left(nullptr), _right(nullptr) {}
};

template<class K>
class BSTree {
    typedef BSTNode<K> Node;
private:
    Node* _root = nullptr;
    
    // 递归中序遍历
    void _InOrder(Node* root) {
        if (root == nullptr) return;
        _InOrder(root->_left);
        std::cout << root->_key << " ";
        _InOrder(root->_right);
    }
    
public:
    // 插入、查找、删除等方法如前文所示
    void InOrder() {
        _InOrder(_root);
        std::cout << std::endl;
    }
};

4.2 扩展版本（Key-Value模型）

在标准版本的基础上，我们引入了Key-Value存储模型来增强数据结构的灵活性和查询效率。这个扩展版本特别适合需要快速查找和动态更新的应用场景。

主要特性：

  1. 灵活的键值对存储：每个数据项都由唯一的键（Key）和对应的值（Value）组成

    • 键通常采用字符串或数字类型

    • 值可以是任意数据结构（字符串、数字、数组、对象等）

    • 示例：{"user_id": 123, "name": "张三", "orders": 1001,1002}

  2. 高效查询机制：

    • 支持精确键查询（O(1)时间复杂度）

    • 可选的二级索引支持范围查询

cpp 复制代码 
template<class K, class V>
struct BSTNode {
    K _key;
    V _value;
    BSTNode<K, V>* _left;
    BSTNode<K, V>* _right;

    BSTNode(const K& key, const V& value)
        : _key(key), _value(value), _left(nullptr), _right(nullptr) {}
};

template<class K, class V>
class BSTree {
    typedef BSTNode<K, V> Node;
private:
    Node* _root = nullptr;
    
public:
    // 插入方法
    bool Insert(const K& key, const V& value) {
        if (_root == nullptr) {
            _root = new Node(key, value);
            return true;
        }

        Node* parent = nullptr;
        Node* cur = _root;
        while (cur) {
            if (cur->_key < key) {
                parent = cur;
                cur = cur->_right;
            } else if (cur->_key > key) {
                parent = cur;
                cur = cur->_left;
            } else {
                return false; // 键已存在
            }
        }
        
        cur = new Node(key, value);
        if (parent->_key < key) {
            parent->_right = cur;
        } else {
            parent->_left = cur;
        }
        return true;
    }
    
    // 查找方法，返回节点指针以便修改value
    Node* Find(const K& key) {
        Node* cur = _root;
        while (cur) {
            if (cur->_key < key) {
                cur = cur->_right;
            } else if (cur->_key > key) {
                cur = cur->_left;
            } else {
                return cur;
            }
        }
        return nullptr;
    }
};

五、二叉搜索树的应用场景

5.1 key搜索场景

场景特点：只需要判断关键字是否存在，不关心关联值。

只有key作为关键码，结构中只需要存储key即可，关键码即为需要搜索到的值，搜索场景只需要判断key在不在。key的搜索场景实现的二叉树搜索树支持增删查，但是不支持修改，修改key破坏搜索树结构了。

场景1：小区无人值守车库，小区车库买了车位的业主车才能进小区，那么物业会把买了车位的业主的车牌号录入后台系统，车辆进入时扫描车牌在不在系统中，在则抬杆，不在则提示非本小区车辆，无法进入。

代码实现：

cpp 复制代码 
// 车牌检查系统
BSTree<std::string> carSystem;
carSystem.Insert("京A12345");
carSystem.Insert("沪B67890");

// 车辆入场检查
std::string licensePlate = "京A12345";
if (carSystem.Find(licensePlate)) {
    std::cout << "允许进入" << std::endl;
} else {
    std::cout << "未授权车辆" << std::endl;
}

5.2 Key-Value模型应用场景

场景特点：需要通过关键字查找对应的关联值。

每一个关键码key，都有与之对应的值value，value可以是任意类型对象。树的结构中（结点）除了需要存储key，还要存储对应的value，增/删/查还是以key为关键字走二叉搜索树的规则进行比较，可以快速查找到key对应的value。key/value的搜索场景实现的二叉搜索树支持修改，但是不支持修改key，修改key会破坏搜索树性质，可以修改value。

场景1：商场无人值守车库，入口进场时扫描车牌，记录车牌和入场时间，出口离场时，扫描车牌，查找入场时间，用当前时间-入场时间计算出停车时长，计算出停车费用，缴费后抬杆，车辆离场。

代码示例：

cpp 复制代码 
// 单词统计系统
BSTree<std::string, int> wordCount;
std::vector<std::string> words = {"apple", "banana", "apple", "orange", "banana", "apple"};

for (const auto& word : words) {
    auto node = wordCount.Find(word);
    if (node == nullptr) {
        wordCount.Insert(word, 1);
    } else {
        node->_value++;
    }
}

// 输出统计结果
// 中序遍历会按字典序输出

六、总结

二叉搜索树作为一种基础而重要的数据结构，具有以下特点：

优点：

  • 动态性能好，支持高效插入删除

  • 中序遍历可得有序序列

  • 实现相对简单

缺点：

  • 普通BST可能退化为链表

  • 需要平衡机制保证性能

适用场景：

  • 需要动态维护有序数据集

  • 查找、插入、删除操作都较频繁

  • 数据量不是特别大，或可以使用平衡BST

掌握二叉搜索树不仅是学习更高级数据结构的基础，也是理解许多系统底层实现的关键。在实际应用中，我们通常使用其平衡变种（如红黑树）来保证稳定性能。

相关推荐
fangzhanpeng1682 天前
快速掌握C#语言基础知识点（1.基础数据类型）
开发语言·c#·1024程序员节
无己心4 天前
面向多平台 AI 搜索引擎的适配层架构设计
前端·人工智能·搜索引擎·ai·1024程序员节
u01030552710 天前
AI驱动的安卓UI自动生成功能实现
人工智能·1024程序员节
u01030552710 天前
长株潭智能体赋能腾讯元器链接共享
1024程序员节
云贝贝贝12 天前
OceanBase认证体系介绍与备考指南
运维·服务器·oceanbase·1024程序员节
u01030552712 天前
Java图像处理实战指南
人工智能·1024程序员节
u01030552712 天前
Java AWT鼠标事件全解析
人工智能·1024程序员节
u01030552715 天前
Java实用类应用精讲
人工智能·1024程序员节
u01030552715 天前
Java I/O核心操作实战
人工智能·1024程序员节
u01030552716 天前
ArrayList操作详解与实战应用
人工智能·1024程序员节
热门推荐
01国内可直接用、免费额度/永久免费的大模型API清单（含 SiliconFlow、火山、阿里、智谱、百度、Kimi、DeepSeek、DMXAPI 等）02GitHub 镜像站点03微信历史版本含下载地址（ Windows PC | 安卓 | MAC ）及设置微信不更新042026 国产 AI 大模型横评：DeepSeek、通义千问、Kimi、文心一言、星火、豆包谁更能打？05历年考研数学一、数学二、数学三真题试卷及答案PDF06Agnes AI 免费 API 接入指南：文本、生图、生视频，一套接口全免费07AI 编程 IDE 全景解析 2026：Agent 全面接管开发链路08VSCode+CodeX扩展，无法启动092026年7月AI圈大地震：GPT-5.6被政府限制、Claude入驻Slack、Anthropic自研芯片10如何新建文件夹？ 电脑新建文件夹的4种方法