图的邻接矩阵实现以及遍历
文章目录
- 图的邻接矩阵实现以及遍历
-
- 一、前言
- 二、图的遍历
-
- [2.1 深搜( D F S DFS DFS)](#2.1 深搜( D F S DFS DFS))
-
- [2.1.1 概念](#2.1.1 概念)
- [2.1.2 思想](#2.1.2 思想)
- [2.1.3 过程](#2.1.3 过程)
- [2.2 广搜( B F S BFS BFS)](#2.2 广搜( B F S BFS BFS))
-
- [2.2.1 概念](#2.2.1 概念)
- [2.2.2 过程](#2.2.2 过程)
- 三、邻接矩阵的实现
-
- [3.1 定义图结构](#3.1 定义图结构)
- [3.2 初始化](#3.2 初始化)
- [3.3 添边](#3.3 添边)
- [3.4 访问](#3.4 访问)
- [3.5 深搜](#3.5 深搜)
- [3.6 广搜](#3.6 广搜)
- 小结
一、前言
上文图的基本概述中已经对图的存储结构进行了一个深入解析,但是具体怎么实现 呢?今天我就来挑战一下~当有了图,就像对树一样,我们需要对图中的元素进行访问处理 ,因此需要遍历这一关键的操作,那这又该怎样实现呢?且停留片刻,相信你一定能摸清里面的门道~
二、图的遍历
同样作为非线性结构,图的遍历和树的遍历思想基本一致 ,其遍历可分为:深搜 ( D F S DFS DFS),广搜 ( B F S BFS BFS)
唯一的区别 :图的元素与元素之间是: m : n m:n m:n,会出现重复遍历已访问过的节点。而树不会出现这个问题(往上看只有一个元素)。接下来我将对其进行深入解读~
2.1 深搜( D F S DFS DFS)
2.1.1 概念
一条道走到黑。
2.1.2 思想
递归
2.1.3 过程
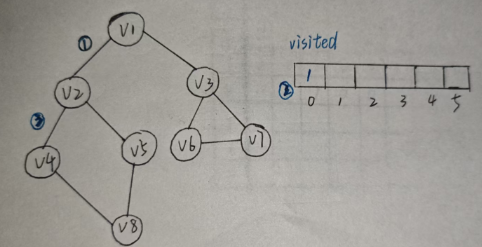
首先,有一个既定的原则 :节点的访问由小到大 ( V 1 V1 V1, V 2 V2 V2...)。
为了防止重复遍历,需要引入visited数组,记录已经处理的节点。
如图:
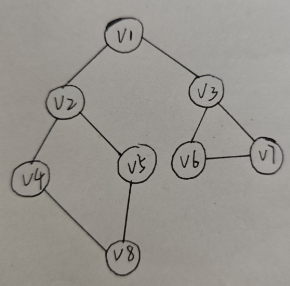
从 V 1 V1 V1开始,可以到 V 2 , V 3 V2,V3 V2,V3,由于从小到大,因此到 V 2 V2 V2。 V 2 V2 V2可以到 V 1 , V 4 , V 5 V1,V4,V5 V1,V4,V5, V 1 V1 V1遍历过了,于是到 V 4 V4 V4。继续遍历,直到 V 5 V5 V5,无路可走,只能回溯,每回退一次,查看是否有遗漏的没遍历的路径,直到最后一个点。
最终结果 : V 1 − > V 2 − > V 4 − > V 8 − > V 5 − > V 3 − > V 6 − > V 7 V1->V2->V4->V8->V5->V3->V6->V7 V1−>V2−>V4−>V8−>V5−>V3−>V6−>V7
2.2 广搜( B F S BFS BFS)
2.2.1 概念
广搜是层次遍历 ,就像是"水面波纹"、"病毒感染",由里及外地探索可以触及的点(由本身的点能连接到的点)。
2.2.2 过程
但是基于遍历本身需要有先后之分,因此需要对"可触及的点"进行一个临时存储 ------队列。
同时在访问过程中,同样需要定义一个visited数组,记录已进入队列 的(只要进过队列,就进行记录),以防止重复遍历。
每出队一个点(进行处理),就继续将其"所能接触到的点"入队。
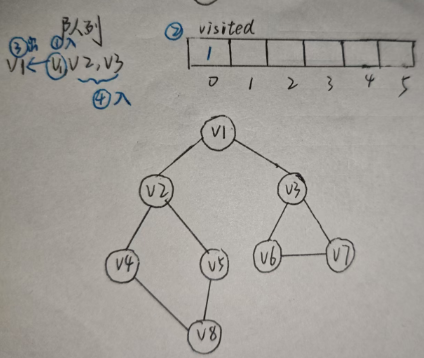
如图:
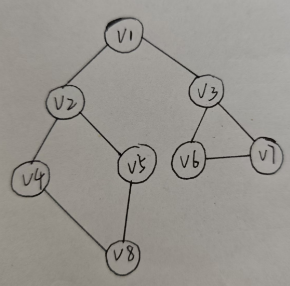
V 1 V1 V1入队(标记为已访问), V 1 V1 V1出队(处理 V 1 V1 V1), V 2 V2 V2, V 3 V3 V3入队(标记), V 2 V2 V2出队(处理), V 4 V4 V4, V 5 V5 V5入队(标记),以此不断循环。
最终结果 : V 1 − > V 2 − > V 3 − > V 4 − > V 5 − > V 6 − > V 7 − > V 8 V1->V2->V3->V4->V5->V6->V7->V8 V1−>V2−>V3−>V4−>V5−>V6−>V7−>V8
三、邻接矩阵的实现
3.1 定义图结构
c
// 定义数量------便于申请时预留空间
#define MaxNodeNum 20
// 定义一个足够大的值(表示边的权值)
#define INF 1E4
// 邻接矩阵的顶点结构
typedef struct
{
int no; // 顶点编号
char *show; // 显示顶点信息
} MatrixVertex;
// 表示边
typedef int MatrixEdge;
// 图的邻接矩阵表示法
typedef struct
{
MatrixVertex vex[MaxNodeNum]; // 点集(一维数组)
int NodeNum; // 对数量进行限制
MatrixEdge edges[MaxNodeNum][MaxNodeNum]; // 边集(矩阵)
int edgeNum; // 边的数量
int directed; // 表示是否有向
} MGraph;3.2 初始化
初始化点集合边集
如图:
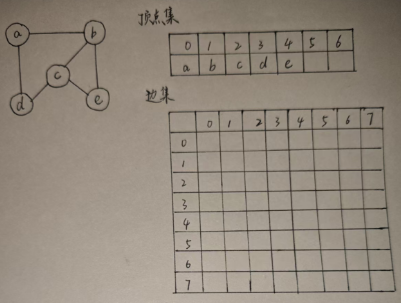
c
// 初始化图
void initMGraph(MGraph *graph, char *names[], int num, int directed, int edgeValue)
{
graph->directed = directed;
graph->nodeNum = num; // 自己定义好的
graph->edgeNum = 0; // 边需要自己建立
// 初始化点集
memset(graph->vex, 0, sizeof(graph->vex));
// 初始化边集,当节点数量为n时,边的最大数量为n^2(每一个顶点都可以和其他任意的顶点建立边,
// 包括它自己)
memset(graph->edges, 0, sizeof(MatrixEdge) * MaxNodeNum * MaxNodeNum);
for(int i = 0; i < num; ++i)
{
// 初始化顶点信息
graph->vex[i].no = i;
graph->vex.show = names[i];
// 初始化边
for(int j = 0; j < num; ++j)
{
graph->edges[i][j] = edgeValue; // 二维数组中存在的值(表示边的连接情况)
}
}
}3.3 添边
- 判断边的合法性
- 填充矩阵
edgeValue
如图(最终):
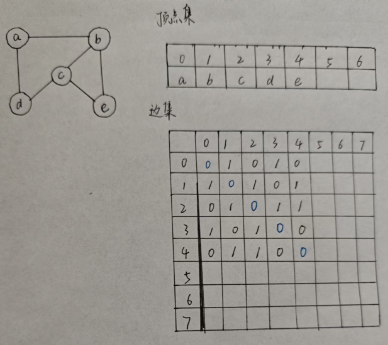
c
// 判断边
static int isEdge(int weight)
{
if(weight > 0 && weight < INF)
{
return 1;
}
return 0;
}
// 添加边
void addMGraphEdge(MGraph *graph, int x, int y, int w)
{
// 判断横坐标是否合法
if(x < 0 || x > graph->nodeNum)
{
return;
}
// 判断纵坐标是否合法
if(y < 0 || y > graph->nodeNum)
{
return;
}
if(!isEdge(graph->edges[x][y]))
{
graph->edges[x][y] = w;
if(graph->directed == 0)
{
// 只有当图为无向图时,才需要存储这个信息
graph->edges[y][x] = w;
}
graph->edgeNum++;
}
}3.4 访问
easy~
c
void visitMGraphNode(MatrixVertex *node)
{
printf("\t%s", node->show);
}3.5 深搜
- 访问顶点,标记顶点
- 从上述顶点出发,继续遍历可访问的顶点(按从小到大的顺序),循环上述过程
如图:
c
// 定义已访问的空间(全局变量,BFS也会用到)
static int MGraphVisited[MaxNodeNum];
// 深搜
void DFS_MGraph(MGraph *graph, int v)
{
// 访问
visitMGraphNode(graph->vex[v]);
// 标记
MGraphVisited[v] = 1;
for(int i = 0; i < graph->nodeNum; ++i)
{
if(isEdge(graph->edges[v][i]) && MGraphVisited[i] == 0)
{
DFS_MGraph(graph, i); // 递归
}
}
}3.6 广搜
- 定义一个临时队列
- 入队顶点,标记为已访问
- 出队顶点,访问,(从该顶点出发)入队可访问的顶点
- 循环上述过程
如图:
c
// 注意:当同时调用DFS和BFS时,因为两种遍历都需要用到标记访问的数组,因此在中间需要有一个清零的过程
void initVisited()
{
memset(MGraphVisited, 0, sizeof(MGraphVisited));
}
// 广搜
void BFS_MGraph(MGraph *graph, int v)
{
int que[MaxNodeNum]; // 定义临时队列
int rear = 0, front = 0; int cur; // 定义尾巴,头,要访问的当前顶点
rear = (rear + 1) % MaxNodeNum; // 实现尾指针的循环移动,队尾先加
que[rear] = v; // 入队
MGraphVisited[v] = 1; // 入队之后就进行标记
while (front != rear)
{
front = (front + 1) % MaxNodeNum; // 出队
cur = que[front]; // 取出来
visitMGraphNode(&graph->vex[cur]); // 访问
for (int i = 0; i < graph->nodeNum; ++i) // 继续入队可遍历的节点
{
if (isEdge(graph->edges[cur][i]) && !MGraphVisited[i])
{
rear = (rear + 1) % MaxNodeNum;
que[rear] = i;
MGraphVisited[i] = 1;
}
}
}
}小结
本篇主要以邻接矩阵的实现为主,下篇将会迎来邻接表 哦~期待 i n g ing ing
希望各位不吝赐教~