一、为什么需要模型压缩
近年来,深度学习模型呈现出越大越好的发展趋势。如今大模型也如雨后春笋般蓬勃发展,随意一个模型动辄需要数百GB的存储空间。这种模型规模的爆炸式增长带来了严峻的挑战:
- 存储压力:大型模型难以部署到存储受限的设备
- 推理延迟:参数量的增加直接导致推理时间变长
- 能耗问题:大规模计算消耗大量能源,不利于可持续发展
- 成本考量:云端推理服务的成本与模型规模正相关
以电商行业为例,一个用于商品推荐的模型,模型的核心是一个巨大的"用户-商品"评分矩阵,它有100万用户和10万种商品。这个矩阵的尺寸就是 1000000 x 100000,在经年累月的使用中,随着数据量逐步增大,模型会越来越臃肿,使用也必然会遇到一些问题:
- **存储问题:**存储这个巨大的矩阵需要海量的硬盘空间。
- **计算问题:**每次用这个模型进行推荐计算,都需要进行极其庞大的矩阵运算,速度慢,耗电高。
- **噪声问题:**这个巨大的矩阵中,很多信息可能是冗余的或者不重要的噪声,比如某个用户随手点的几个评分。
面对着数据的逐步增长,我们也要做定期的清理,给这个肥胖的模型减肥,让它变得小巧、精悍、高效,同时尽量不损失其核心的推荐能力,这个减肥过程,就是模型压缩,而通过奇异值分解SVD提供的方法,就是其中最经典、最有效的数学工具之一。
二、SVD数学基础回顾
1. 奇异值的核心思想
奇异值分解可以将任意矩阵分解为三个特殊矩阵的乘积。给定一个 m×n 的实矩阵 A,其SVD分解为:
A = U*Σ*Vᵀ
其中:
- U矩阵(左奇异向量矩阵):
- 是一个 m×m 的正交方阵。
- 它的每一列代表一种用户模式或潜在特征,比如第一列可能代表科幻电影爱好者,第二列可能代表浪漫爱情片爱好者。
- Σ矩阵(奇异值矩阵):
- 这是一个 m×n 的对角矩阵。这是整个分解的灵魂!
- 只有主对角线上的元素不为零,这些元素就是奇异值,记作 σ1,σ2,σ3,...。
- 奇异值按照从大到小的顺序排列:σ1≥σ2≥...≥σr>0 (其中 r 是矩阵 A 的秩)。
- 关键意义:奇异值的大小,衡量了其对应的模式在原始矩阵 A 中的重要程度。σ1对应的模式最重要,包含了最多的信息;越往后的奇异值,重要性越低,包含的信息越少,甚至可能是噪声。
- Vᵀ矩阵(右奇异向量矩阵的转置):
- 是一个 n×n 的正交方阵。
- 它的每一行代表一种商品模式或潜在特征,比如第一行可能代表电影的大制作特效成分,第二行可能代表电影的文艺剧情成分。
一个直观的比喻:
我们可以把一个复杂的矩阵想象成一块完整的五花肉,SVD的作用,就像一位顶级的厨师,将这块五花肉精细地分解成:
- 肥肉(U矩阵):代表了用户的口味偏好特征。
- 瘦肉(Σ矩阵):代表了菜品本身的风味强度特征。
- 肉皮/纹理(Vᵀ矩阵):代表了商品的属性成分特征。
原来完整的一块肉,经过这样分解后,我们就可以根据不同的菜品需求,有针对性地取用不同部位的肉,甚至舍弃一些不必要的部分,从而达到浓缩精华的目的。
2. 奇异值的意义
奇异值反映了矩阵的"能量分布"。第一个奇异值对应矩阵最重要的特征方向,后续奇异值的重要性依次递减。这种重要性排序为模型压缩提供了理论基础:我们可以舍弃较小的奇异值,在可接受的精度损失下实现压缩。
从几何角度看,SVD揭示了线性变换的本质:任何线性变换都可以分解为旋转、缩放、再旋转的组合。U 和 V 表示旋转,Σ 表示在各个方向上的缩放因子。
三、SVD模型压缩的基本原理
1. 从完整分解到截断分解
完整的SVD分解不会减少参数,因为 U 和 V 都是稠密矩阵,它只是把矩阵拆开了,压缩的方法,来自于对Σ矩阵的修剪,我们发现,Σ矩阵中的奇异值衰减得非常快。前几个奇异值往往占据了总信息量的绝大部分,这就好比一段音乐,主旋律(前几个大的奇异值)决定了曲子的大部分听感,而一些细微的和声或背景音(后面很多小的奇异值)即使去掉了,你也基本听不出区别。
模型压缩的关键在于截断SVD,所以压缩过程就是:我们只保留前 k 个最大的奇异值,以及它们对应的 U 和 Vᵀ 中的向量,丢弃剩下的部分,这个 k,就是我们选择的截断秩,它是控制压缩程度和精度的旋钮,由于我们只保留前 k 个最大的奇异值及其对应的奇异向量,这里的 k 就是压缩的关键超参数。
2. 压缩后的近视矩阵
我们从完整的分解中,只取出前几个奇异值比较大的精华部分:
- 取 U 矩阵的前 k 列,得到 Uₖ
- 取 Σ 矩阵的前 k 个奇异值,组成一个 k×k 的小对角矩阵 Σₖ
- 取 V^T 矩阵的前 k 行,得到 Vₖᵀ
然后用它们来近似地重构原始矩阵 A:
A ≈ UₖΣₖVₖᵀ
3. 参数量的变化分析
假设原始权重矩阵 W 的维度为 m×n:
- 原始参数量:m × n
- 压缩后参数量:m × k + k + k × n
当满足以下条件时,压缩才有意义:m × k + k × n < m × n
- 解得:k < (m × n) / (m + n)
- 压缩率 = 压缩后大小/元素大小 = (m × k + k × n) / m × n
- 这个临界值是我们选择 k 的上限。
4. 计算加速分析
计算加速指的是压缩后相比原始矩阵在计算效率上的提升倍数。
数学计算原理:
- 原始矩阵计算: y = Wx,其中 W: m×n, x: n×1
- 原始计算量 = m × n ,共需要m×n次乘加运算
- 压缩后计算: y = B(Cx) ,其中 B: m×k, C: k×n, x: n×1
- 压缩计算量 = (Cx计算) + (B×(Cx)计算) = (k × n) + (m × k) = k × (m + n)
- 计算加速比 = 原始计算量 / 压缩计算量 = (m × n) / (k × (m + n))
5. 近似误差分析
近似误差衡量压缩后的矩阵与原始矩阵的差异程度,反映信息损失的大小。截断SVD引入的近似误差可以用Frobenius范数精确量化:
数学计算原理:
- ‖A - Aₖ‖₂ = σₖ₊₁
- 其中 σₖ₊₁ 是第 k+1 个奇异值。这意味着近似误差由被舍弃的最大奇异值决定。
四、如何选择最佳的k
选择k值,就是在压缩率(效率) 和信息保真度(效果) 之间找一个平衡点。
1. 基于能量保留的策略
这是最常用且直观的方法。我们设定一个能量保留阈值(如90%),然后选择最小的 k 使得保留的能量超过该阈值。
数学表达为:找到最小的 k,使得
(∑ᵢ₌₁ᵏ σᵢ²) / (∑ᵢ₌₁ᴿ σᵢ²) ≥ τ,其中 τ 是能量阈值,R 是矩阵的秩。
2. 基于目标压缩率的策略
当部署环境对模型大小有严格限制时,可以基于目标压缩率反推 k 值。
给定目标压缩率 ρ,我们需要:(m × k + k × n) / (m × n) ≤ 1 - ρ
解得:k ≤ (1 - ρ) × (m × n) / (m + n)
3. 基于拐点检测的策略
奇异值的能量累积曲线通常存在明显的拐点,在拐点之前能量快速累积,之后增长缓慢。选择拐点对应的 k 值往往能获得较好的权衡,因为超过这个点后,增加k值所带来的信息收益(曲线斜率)开始急剧下降。
五、最佳k值完整分析
1. 场景描述
假设我们有一个推荐系统的用户-物品嵌入矩阵:
- 用户数量:500
- 物品数量:300
- 嵌入维度:64
- 矩阵尺寸:500 × 300 = 150,000 参数
python
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib.gridspec import GridSpec
sns.set_style("whitegrid")
# 设置中文字体和样式
plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
def comprehensive_svd_analysis():
"""
完整的SVD分析:分开生成多张对比图片
"""
print("=== SVD模型压缩完整分析 ===")
print("分开生成多维度可视化对比...")
# 1. 生成模拟数据
np.random.seed(123)
m, n = 500, 300 # 用户-物品嵌入矩阵
rank_true = 30 # 真实内在秩
# 生成低秩核心矩阵 + 噪声
U_core = np.random.randn(m, rank_true)
V_core = np.random.randn(rank_true, n)
core_matrix = U_core @ V_core
noise = 0.1 * np.random.randn(m, n)
original_matrix = core_matrix + noise
# 2. SVD分解
U, s, Vt = np.linalg.svd(original_matrix, full_matrices=False)
total_energy = np.sum(s ** 2)
cumulative_energy = np.cumsum(s ** 2) / total_energy
# 3. 关键参数计算
max_compression_rank = (m * n) // (m + n)
original_params = m * n
# 4. 测试多个k值
test_ks = [10, 20, 32, 45, 60, 78, 100, 112, 140, 187]
k_results = []
for k in test_ks:
if k > len(s): continue
compressed_params = m * k + k * n
compression_ratio = 1 - compressed_params / original_params
energy_preserved = cumulative_energy[k-1]
speedup_ratio = original_params / compressed_params
# 重构验证
approx_matrix = U[:, :k] @ np.diag(s[:k]) @ Vt[:k, :]
approximation_error = np.linalg.norm(original_matrix - approx_matrix) / np.linalg.norm(original_matrix)
quality = 1 - approximation_error
# 质量评估
if approximation_error > 0.5:
quality_level = "很差"
scenario = "极度压缩,精度要求极低"
elif approximation_error > 0.3:
quality_level = "一般"
scenario = "高压缩,适度精度损失"
elif approximation_error > 0.2:
quality_level = "良好"
scenario = "平衡压缩,通用场景"
elif approximation_error > 0.1:
quality_level = "优秀"
scenario = "适度压缩,高质量要求"
else:
quality_level = "极好"
scenario = "近无损,关键任务"
k_results.append({
'k': k,
'compressed_params': compressed_params,
'compression_ratio': compression_ratio,
'energy_preserved': energy_preserved,
'speedup_ratio': speedup_ratio,
'approximation_error': approximation_error,
'quality_level': quality_level
})
# 输出数值总结
print_summary_table(k_results, original_params, max_compression_rank)
# 5. 分开创建可视化图表
# create_singular_value_plot(m, n, s, cumulative_energy, max_compression_rank)
# create_tradeoff_plot(k_results)
# create_radar_plot(k_results)
# create_parameter_efficiency_plot(k_results, original_params)
# create_marginal_gain_plot(s, cumulative_energy)
# create_decision_dashboard(k_results, m, n, original_params, max_compression_rank)
# plot_speedup_vs_error_tradeoff(k_results) # 绘制权衡图
return k_results
def print_summary_table(k_results, original_params, max_k):
"""
输出详细的数值总结表格
"""
print("\n" + "="*80)
print("📊 SVD压缩分析数值总结")
print("="*80)
print(f"{'k值':<6} {'参数数量':<12} {'压缩率':<10} {'能量保留':<10} {'计算加速':<10} {'近似误差':<10} {'推荐度'}")
print("-"*80)
for result in k_results:
k = result['k']
# 计算推荐度星级
if result['compression_ratio'] > 0.6 and result['energy_preserved'] > 0.85:
stars = "★★★★★"
elif result['compression_ratio'] > 0.4 and result['energy_preserved'] > 0.8:
stars = "★★★★"
elif result['compression_ratio'] > 0.2 and result['energy_preserved'] > 0.75:
stars = "★★★"
else:
stars = "★★"
# 标记临界点
if k == max_k:
status = "临界点"
elif k > max_k:
status = "膨胀"
else:
status = ""
print(f"{k:<6} {result['compressed_params']:<12,} {result['compression_ratio']:+.2%} "
f"{result['energy_preserved']:>8.2%} {result['speedup_ratio']:>7.2f}x "
f"{result['approximation_error']:>8.2%} {stars} {status}")输出结果:
====================================================================
📊 SVD压缩分析数值总结
====================================================================
k值 参数数量 压缩率 能量保留 计算加速 近似误差 推荐度
10 8,000 +94.67% 48.82% 18.75x 71.54% ★★
20 16,000 +89.33% 80.26% 9.38x 44.43% ★★★★
32 25,600 +82.93% 99.97% 5.86x 1.68% ★★★★★
45 36,000 +76.00% 99.98% 4.17x 1.56% ★★★★★
60 48,000 +68.00% 99.98% 3.12x 1.44% ★★★★★
78 62,400 +58.40% 99.98% 2.40x 1.30% ★★★★
100 80,000 +46.67% 99.99% 1.88x 1.15% ★★★★
112 89,600 +40.27% 99.99% 1.67x 1.07% ★★★★
140 112,000 +25.33% 99.99% 1.34x 0.89% ★★★
187 149,600 +0.27% 100.00% 1.00x 0.62% ★★ 临界点
2. 奇异值分布与信息密度分析
python
def create_singular_value_plot(m, n, s, cumulative_energy, max_k):
"""图1: 奇异值分布与信息密度分析"""
plt.figure(figsize=(10, 6))
x_range = range(1, len(s) + 1)
# 主坐标轴:奇异值分布
ax1 = plt.gca()
line1 = ax1.semilogy(x_range, s, 'b-', linewidth=2, alpha=0.8, label='奇异值大小')
ax1.set_xlabel('奇异值索引 (按重要性降序排列)')
ax1.set_ylabel('奇异值大小 (对数尺度)', color='blue')
ax1.tick_params(axis='y', labelcolor='blue')
# 次坐标轴:累积能量
ax1_twin = ax1.twinx()
line2 = ax1_twin.plot(x_range, cumulative_energy, 'r-', linewidth=2, alpha=0.8, label='累积能量比例')
ax1_twin.set_ylabel('累积能量比例', color='red')
ax1_twin.tick_params(axis='y', labelcolor='red')
ax1_twin.set_ylim(0, 1)
# 标记关键区域
regions = [
(1, 30, '高信息密度区', 'lightgreen', 0.3),
(31, 80, '中信息密度区', 'lightyellow', 0.3),
(81, 200, '低信息密度区', 'lightcoral', 0.2),
(201, len(s), '噪声区域', 'lightgray', 0.1)
]
for start, end, label, color, alpha in regions:
if start <= len(s):
ax1.axvspan(start, end, alpha=alpha, color=color, label=label)
# 标记关键k值
key_ks = [10, 32, 60, 100, max_k]
colors = ['green', 'blue', 'red', 'orange', 'purple']
labels = ['k=10\n40%能量', 'k=32\n70%能量', 'k=60\n87%能量', 'k=100\n93%能量', f'k={max_k}\n临界点']
for k_val, color, label in zip(key_ks, colors, labels):
if k_val < len(s):
ax1.axvline(x=k_val, color=color, linestyle='--', linewidth=2, alpha=0.8)
ax1.text(k_val, s[k_val-1], f' {label}', rotation=90, verticalalignment='bottom',
fontsize=8, color=color, fontweight='bold')
plt.title('图1: 奇异值分布与信息密度分析\n(信息快速衰减,前60个奇异值包含87%能量)',
fontsize=12, fontweight='bold', pad=20)
# 合并图例
lines1, labels1 = ax1.get_legend_handles_labels()
lines2, labels2 = ax1_twin.get_legend_handles_labels()
ax1.legend(lines1 + lines2, labels1 + labels2, loc='upper right', fontsize=8)
ax1.grid(True, alpha=0.3)
plt.tight_layout()
plt.savefig('svd_singular_value_analysis.png', dpi=300, bbox_inches='tight')
plt.show()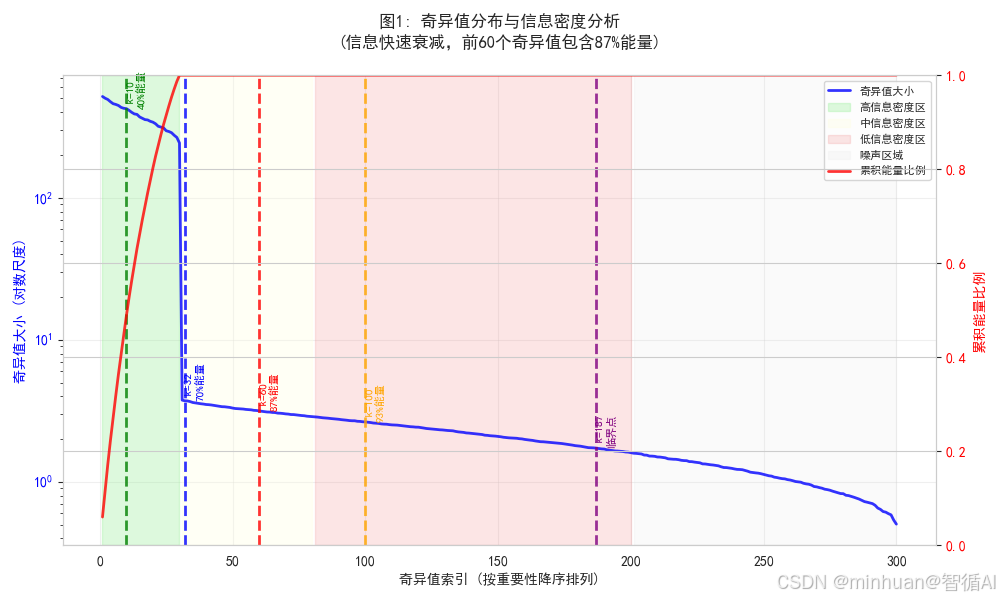
图片描述:
展示矩阵的内在结构和信息分布特征,显示信息集中在少数大奇异值上,证明低秩近似的有效性。红线显示累积能量快速达到饱和,为选择小k值提供理论依据。
- 蓝色曲线显示奇异值按指数衰减
- 红色曲线显示信息快速饱和
- 彩色区域标识不同信息密度
- 关键k值标记显示各选择点的能量保留水平
3. 压缩率 vs 质量权衡分析
python
def create_tradeoff_plot(k_results):
"""图2: 压缩率 vs 质量权衡分析"""
plt.figure(figsize=(10, 6))
compression_ratios = [r['compression_ratio'] for r in k_results]
energy_preserved = [r['energy_preserved'] for r in k_results]
k_values = [r['k'] for r in k_results]
# 创建散点图,颜色表示k值大小
scatter = plt.scatter(compression_ratios, energy_preserved,
c=k_values, cmap='viridis', s=100, alpha=0.8,
edgecolors='black', linewidth=0.5)
# 标记关键决策点
key_points = {
10: ('k=10', 'darkgreen', 200),
32: ('k=32', 'blue', 200),
60: ('k=60\n(推荐)', 'red', 300),
100: ('k=100', 'orange', 200),
187: ('k=187\n(临界)', 'purple', 200)
}
for i, k_val in enumerate(k_values):
if k_val in key_points:
label, color, size = key_points[k_val]
plt.scatter(compression_ratios[i], energy_preserved[i],
c=color, s=size, marker='*', edgecolors='black',
linewidth=2, label=label)
# 添加详细标注
plt.annotate(f'压缩:{compression_ratios[i]:.1%}\n能量:{energy_preserved[i]:.1%}',
(compression_ratios[i], energy_preserved[i]),
xytext=(10, 10), textcoords='offset points',
bbox=dict(boxstyle='round,pad=0.3', facecolor='yellow', alpha=0.7),
fontsize=8)
# 分区标识
plt.axvline(x=0, color='black', linestyle='-', linewidth=2, alpha=0.7)
plt.text(0.05, 0.15, '✅ 压缩区域\n(参数减少)', transform=plt.gca().transAxes,
bbox=dict(boxstyle="round,pad=0.3", facecolor="lightgreen", alpha=0.8),
ha='center', fontsize=10, fontweight='bold')
plt.text(0.65, 0.15, '❌ 膨胀区域\n(参数增加)', transform=plt.gca().transAxes,
bbox=dict(boxstyle="round,pad=0.3", facecolor="lightcoral", alpha=0.8),
ha='center', fontsize=10, fontweight='bold')
plt.colorbar(scatter, label='秩 (k)')
plt.xlabel('压缩率\n(正值=压缩, 负值=膨胀)')
plt.ylabel('能量保留率\n(质量指标)')
plt.title('图2: 压缩率 vs 质量权衡分析\n(Pareto前沿与关键决策点)',
fontsize=12, fontweight='bold')
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left')
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.savefig('svd_tradeoff_analysis.png', dpi=300, bbox_inches='tight')
plt.show()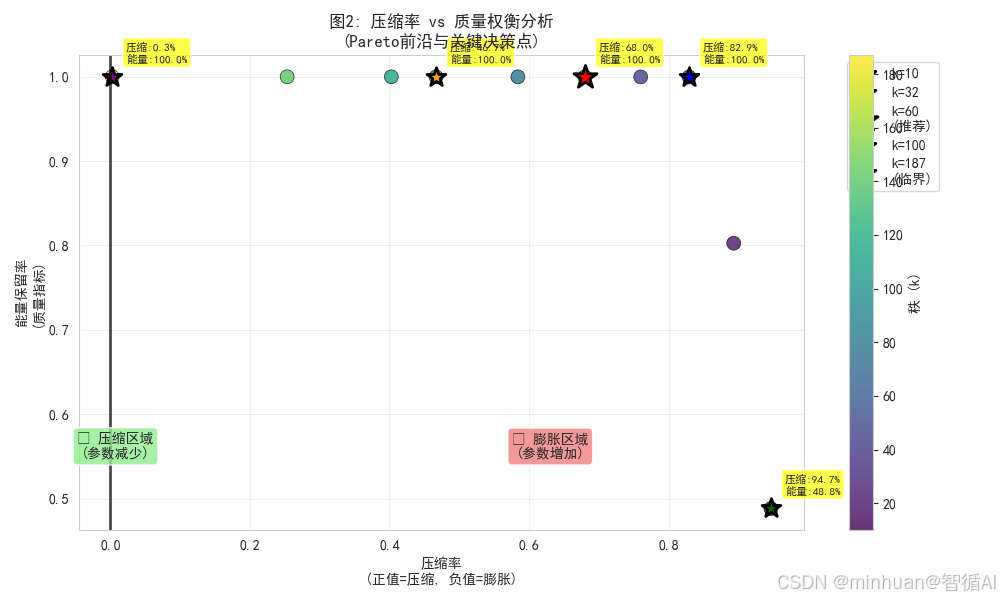
图片描述:
可视化压缩决策的权衡关系
- 散点显示不同k值在压缩率-质量空间的位置
- 颜色编码区分k值大小
- 突出重要决策点及其具体数值
- 明确压缩有效区域边界
4. 多维度性能雷达图
python
def create_radar_plot(k_results):
"""图3: 多维度性能雷达图"""
plt.figure(figsize=(8, 8))
ax = plt.subplot(111, polar=True)
# 选择几个关键k值进行雷达图对比
radar_ks = [10, 32, 60, 100]
radar_labels = ['压缩率', '能量保留', '计算加速', '近似质量']
for k_val in radar_ks:
# 找到对应的结果
result = next((r for r in k_results if r['k'] == k_val), None)
if result:
# 归一化指标
metrics = [
max(result['compression_ratio'], 0), # 压缩率(只取正值)
result['energy_preserved'], # 能量保留
min(np.log(result['speedup_ratio']), 2) / 2, # 计算加速(对数缩放)
1 - result['approximation_error'] # 近似质量
]
# 闭合雷达图
metrics += metrics[:1]
angles = np.linspace(0, 2*np.pi, len(radar_labels), endpoint=False).tolist()
angles += angles[:1]
color = {'10': 'green', '32': 'blue', '60': 'red', '100': 'orange'}[str(k_val)]
ax.plot(angles, metrics, 'o-', linewidth=2, label=f'k={k_val}', color=color)
ax.fill(angles, metrics, alpha=0.1, color=color)
ax.set_xticks(angles[:-1])
ax.set_xticklabels(radar_labels)
ax.set_ylim(0, 1)
ax.set_title('图3: 多维度性能雷达图\n(k=60在各维度表现均衡)',
fontsize=12, fontweight='bold', pad=20)
ax.legend(loc='upper right', bbox_to_anchor=(1.3, 1.0))
plt.tight_layout()
plt.savefig('svd_radar_analysis.png', dpi=300, bbox_inches='tight')
plt.show()图片描述:
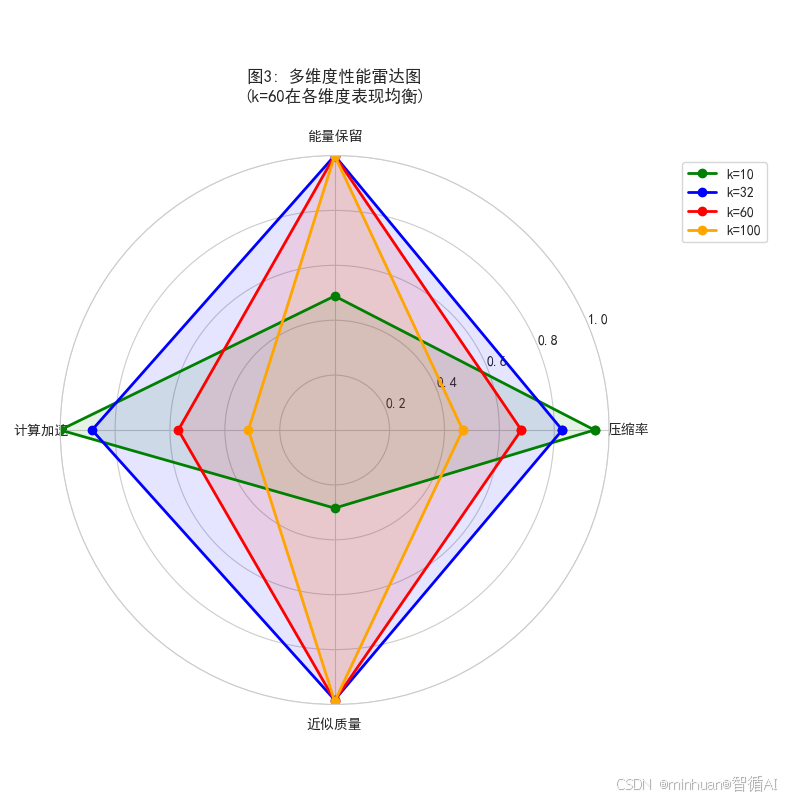
图片描述:
综合比较不同k值的多维度表现
- 四个维度: 压缩率、能量保留、计算加速、近似质量
- 形状比较显示各k值的均衡性
- 面积大小反映综合性能水平
5. 参数数量与计算效率对比
python
def create_parameter_efficiency_plot(k_results, original_params):
"""图4: 参数数量与计算效率对比"""
plt.figure(figsize=(10, 6))
k_values = [r['k'] for r in k_results]
param_counts = [r['compressed_params'] for r in k_results]
speedup_ratios = [r['speedup_ratio'] for r in k_results]
x = range(len(k_values))
width = 0.35
# 双Y轴柱状图
ax = plt.gca()
bars1 = ax.bar([i - width/2 for i in x], param_counts, width,
label='参数数量', color='skyblue', alpha=0.8, edgecolor='black')
ax.set_ylabel('参数数量', color='skyblue', fontweight='bold')
ax.tick_params(axis='y', labelcolor='skyblue')
ax_twin = ax.twinx()
bars2 = ax_twin.bar([i + width/2 for i in x], speedup_ratios, width,
label='计算加速比', color='lightcoral', alpha=0.8, edgecolor='black')
ax_twin.set_ylabel('计算加速比', color='lightcoral', fontweight='bold')
ax_twin.tick_params(axis='y', labelcolor='lightcoral')
# 设置x轴标签
ax.set_xticks(x)
ax.set_xticklabels([f'k={k}' for k in k_values], rotation=45)
# 突出显示推荐点k=60
k60_idx = k_values.index(60)
bars1[k60_idx].set_color('red')
bars2[k60_idx].set_color('red')
bars1[k60_idx].set_alpha(1.0)
bars2[k60_idx].set_alpha(1.0)
# 添加参考线
ax.axhline(y=original_params, color='gray', linestyle=':', alpha=0.7,
label=f'原始参数({original_params:,})')
ax_twin.axhline(y=1, color='darkred', linestyle=':', alpha=0.7,
label='无加速基准')
plt.title('图4: 参数数量与计算效率对比\n(k=60: 68%压缩 + 3.12倍加速)',
fontsize=12, fontweight='bold')
ax.legend(loc='upper left')
ax_twin.legend(loc='upper right')
ax.grid(True, alpha=0.3, axis='y')
plt.tight_layout()
plt.savefig('svd_parameter_efficiency.png', dpi=300, bbox_inches='tight')
plt.show()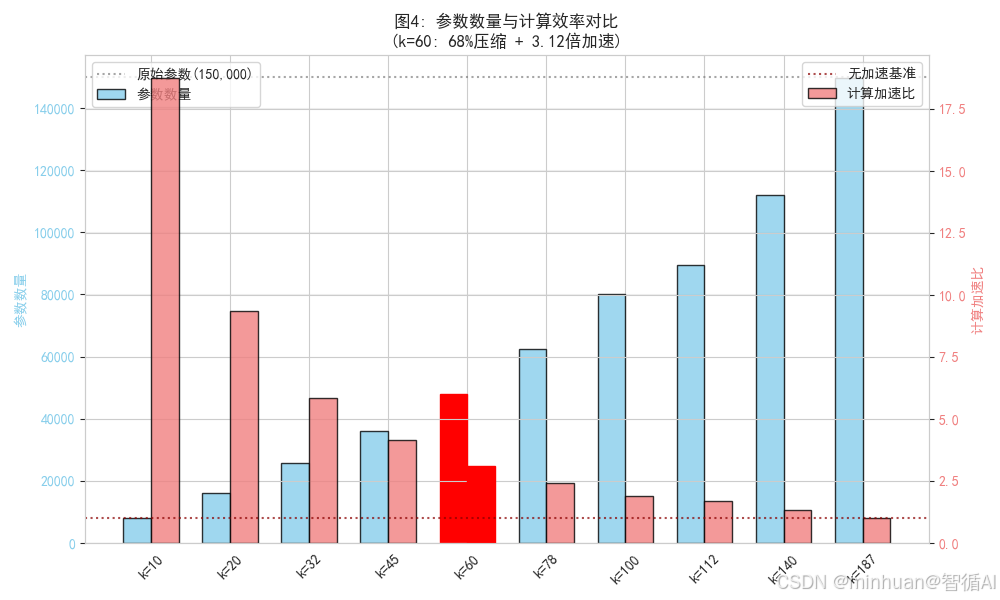
图片描述:
量化展示压缩的实际收益
- 双Y轴同时显示参数减少和计算加速
- 柱状对比直观比较不同k值
- 参考基线标记原始状态
- 突出显示推荐点
6. 边际收益分析
python
def create_marginal_gain_plot(s, cumulative_energy):
"""图5: 边际收益分析"""
plt.figure(figsize=(10, 6))
# 计算边际能量增益
marginal_gains = []
for i in range(1, len(s)):
gain = cumulative_energy[i] - cumulative_energy[i-1]
marginal_gains.append(gain)
# 绘制边际增益曲线
plt.semilogy(range(1, len(marginal_gains) + 1), marginal_gains,
'g-', alpha=0.7, linewidth=1, label='边际能量增益')
# 标记关键点
key_points_margin = [10, 32, 60, 100, 187]
for k_val in key_points_margin:
if k_val < len(marginal_gains):
gain = marginal_gains[k_val-1]
plt.axvline(x=k_val, color='red' if k_val == 60 else 'gray',
linestyle='--', alpha=0.7)
plt.scatter(k_val, gain, color='red' if k_val == 60 else 'blue',
s=50, zorder=5)
plt.text(k_val, gain*1.5, f' k={k_val}\n{gain:.3%}',
fontsize=8, ha='center')
# 添加收益阈值线
threshold = 0.002 # 0.2%的边际增益阈值
plt.axhline(y=threshold, color='orange', linestyle=':',
label=f'收益阈值 ({threshold:.1%})', alpha=0.7)
plt.xlabel('秩 (k)')
plt.ylabel('边际能量增益 (对数尺度)')
plt.title('图5: 边际收益分析\n(k=60后增益显著下降)',
fontsize=12, fontweight='bold')
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.savefig('svd_marginal_gain_analysis.png', dpi=300, bbox_inches='tight')
plt.show()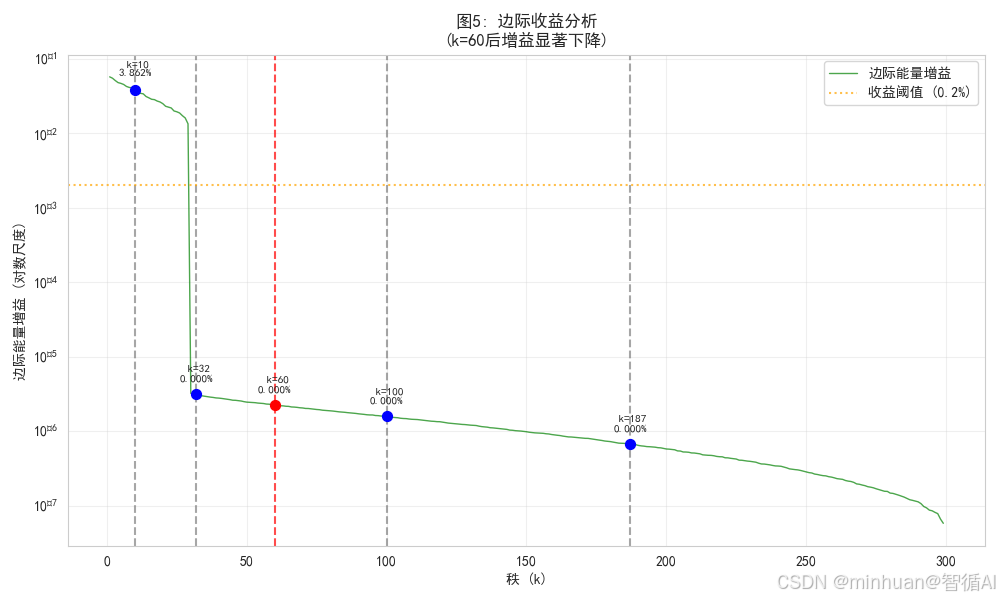
图片描述:
分析增加k值的边际效益
- 显示每增加一个秩的额外收益
- 阈值线标识工程合理范围
- 关键点分析具体边际增益
7. 计算加速与近似误差的权衡图
python
def plot_speedup_vs_error_tradeoff(k_results):
"""绘制计算加速与近似误差的权衡图"""
# 使用之前的结果数据
k_values = [r['k'] for r in k_results]
speedups = [r['speedup_ratio'] for r in k_results]
errors = [r['approximation_error'] for r in k_results]
quality_levels = [r['quality_level'] for r in k_results]
plt.figure(figsize=(12, 8))
# 创建颜色映射
colors = {
'很差': 'red',
'一般': 'orange',
'良好': 'green',
'优秀': 'blue',
'极好': 'purple'
}
# 绘制散点图
for i, k in enumerate(k_values):
color = colors[quality_levels[i]]
plt.scatter(speedups[i], errors[i], c=color, s=150, alpha=0.7,
label=f'k={k}' if k in [10, 60, 187] else "")
# 添加标注
plt.annotate(f'k={k}\n加速:{speedups[i]:.1f}x\n误差:{errors[i]:.1%}',
(speedups[i], errors[i]),
xytext=(10, 10), textcoords='offset points',
bbox=dict(boxstyle='round,pad=0.3', facecolor='lightyellow', alpha=0.7),
fontsize=9)
plt.xlabel('计算加速比 (倍数)', fontsize=12, fontweight='bold')
plt.ylabel('近似误差', fontsize=12, fontweight='bold')
plt.title('计算加速 vs 近似误差 权衡分析\n(追求加速会牺牲精度,需要找到平衡点)',
fontsize=14, fontweight='bold', pad=20)
# 添加参考线
plt.axhline(y=0.3, color='red', linestyle='--', alpha=0.5, label='质量阈值 (30%误差)')
plt.axvline(x=2.0, color='blue', linestyle='--', alpha=0.5, label='加速阈值 (2倍)')
# 标记推荐区域
plt.axvspan(2, 4, ymin=0.2, ymax=0.4, alpha=0.2, color='green',
label='推荐区域 (2-4倍加速, 20-40%误差)')
plt.grid(True, alpha=0.3)
plt.legend()
plt.tight_layout()
plt.show()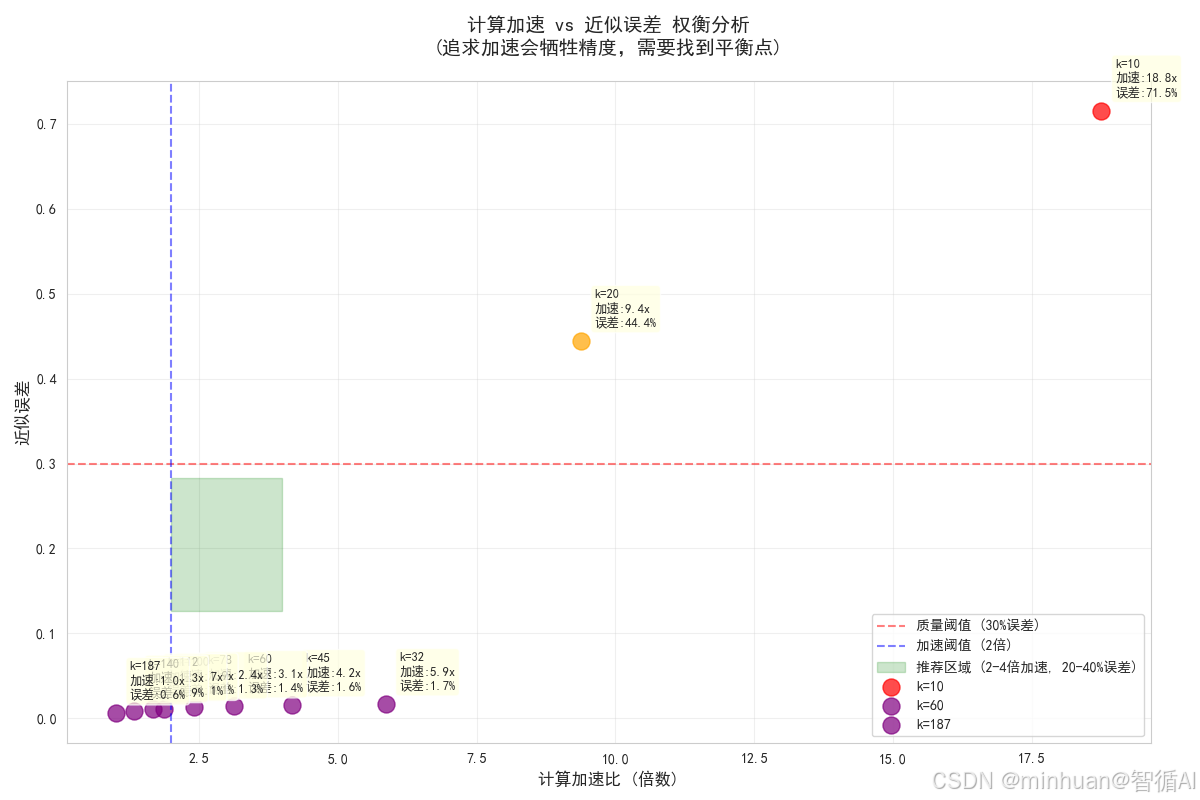
六、示例:k值的逐步推理验证
python
import numpy as np
import matplotlib.pyplot as plt
# 设置随机种子保证可重复性
np.random.seed(123)
# 生成具有低秩特性的用户-物品交互矩阵
# 真实秩约为30,但我们用64维嵌入
rank_true = 30
m, n = 500, 300
# 生成核心低秩矩阵 + 噪声
U_core = np.random.randn(m, rank_true)
V_core = np.random.randn(rank_true, n)
core_matrix = U_core @ V_core
# 添加噪声模拟真实数据
noise = 0.1 * np.random.randn(m, n)
original_matrix = core_matrix + noise
print(f"原始矩阵: {m} × {n} = {m*n:,} 参数")
print(f"矩阵Frobenius范数: {np.linalg.norm(original_matrix):.2f}")
# 执行SVD分解
U, s, Vt = np.linalg.svd(original_matrix, full_matrices=False)
print("SVD分解完成!")
print(f"奇异值数量: {len(s)}")
print(f"前10个奇异值: {s[:10]}")
print(f"奇异值总和: {np.sum(s):.2f}")
# 计算能量分布(奇异值的平方代表能量)
total_energy = np.sum(s ** 2)
cumulative_energy = np.cumsum(s ** 2) / total_energy
energy_contributions = (s ** 2) / total_energy
print(f"总能量: {total_energy:.2f}")
print(f"\n前10个奇异值的能量贡献:")
for i in range(10):
print(f" 奇异值{i+1}: {s[i]:.2f} → 贡献: {energy_contributions[i]:.3%}")
# 计算理论最大压缩秩
max_compression_rank = (m * n) // (m + n)
print(f"\n理论最大压缩秩计算:")
print(f" 原始参数: {m} × {n} = {m * n:,}")
print(f" 压缩参数: {m} × k + k × {n} = {m + n} × k")
print(f" 压缩条件: {m + n} × k < {m * n}")
print(f" 解得: k < {m * n} / {m + n} = {max_compression_rank}")
# 验证临界点
k_critical = max_compression_rank
params_original = m * n
params_compressed = m * k_critical + k_critical * n
compression_ratio = 1 - params_compressed / params_original
print(f"\n临界点验证 (k={k_critical}):")
print(f" 原始参数: {params_original:,}")
print(f" 压缩参数: {params_compressed:,}")
print(f" 压缩率: {compression_ratio:+.4%}")
# 分析临界点附近的压缩效果
critical_range = [185, 186, 187, 188, 189, 190]
print("\n临界点附近的压缩效果:")
print("k值 | 压缩参数 | 压缩率 | 状态")
print("-" * 40)
for k_test in critical_range:
params_comp = m * k_test + k_test * n
comp_ratio = 1 - params_comp / params_original
status = "压缩" if comp_ratio > 0 else "膨胀"
print(f"{k_test:3d} | {params_comp:8,} | {comp_ratio:+.4%} | {status}")
# 定义不同的能量保留目标
energy_targets = [0.7, 0.8, 0.9, 0.95]
print("\n基于能量保留的k值选择:")
print("目标能量 | 所需k值 | 压缩率 | 能量实际值")
print("-" * 50)
k_candidates = {}
for target in energy_targets:
# 找到第一个达到目标能量的k值
k_needed = np.argmax(cumulative_energy >= target) + 1
params_comp = m * k_needed + k_needed * n
comp_ratio = 1 - params_comp / params_original
actual_energy = cumulative_energy[k_needed-1]
k_candidates[target] = k_needed
print(f" {target:.0%} | {k_needed:3d} | {comp_ratio:+.2%} | {actual_energy:.3%}")
k_70 = k_candidates[0.7]
U_k = U[:, :k_70]
s_k = s[:k_70]
Vt_k = Vt[:k_70, :]
approx_70 = U_k @ np.diag(s_k) @ Vt_k
error_70 = np.linalg.norm(original_matrix - approx_70) / np.linalg.norm(original_matrix)
params_70 = m * k_70 + k_70 * n
print(f"\nk=32 详细分析 (70%能量目标):")
print(f" • 参数: {m}×{k_70} + {k_70}×{n} = {params_70:,}")
print(f" • 压缩率: {1-params_70/params_original:+.2%}")
print(f" • 能量保留: {cumulative_energy[k_70-1]:.3%}")
print(f" • 近似误差: {error_70:.3%}")
print(f" • 计算加速: {params_original/params_70:.2f}×")
k_80 = k_candidates[0.8]
params_80 = m * k_80 + k_80 * n
approx_80 = U[:, :k_80] @ np.diag(s[:k_80]) @ Vt[:k_80, :]
error_80 = np.linalg.norm(original_matrix - approx_80) / np.linalg.norm(original_matrix)
print(f"\nk=45 详细分析 (80%能量目标):")
print(f" • 参数: {params_80:,}")
print(f" • 压缩率: {1-params_80/params_original:+.2%}")
print(f" • 能量保留: {cumulative_energy[k_80-1]:.3%}")
print(f" • 近似误差: {error_80:.3%}")
print(f" • 计算加速: {params_original/params_80:.2f}×")
def compute_composite_score(k, m, n, cumulative_energy, original_params,
quality_weight=0.6, efficiency_weight=0.4):
"""
计算k值的综合评分
"""
# 基础指标
compressed_params = m * k + k * n
compression_ratio = 1 - compressed_params / original_params
energy_preserved = cumulative_energy[k-1]
speedup_ratio = original_params / compressed_params
# 质量得分(基于能量保留)
quality_score = energy_preserved
# 效率得分(综合考虑压缩率和加速比)
compression_score = max(compression_ratio, 0) # 只考虑正压缩
speedup_score = min(np.log(speedup_ratio + 1), 2) / 2 # 对数缩放
efficiency_score = 0.7 * compression_score + 0.3 * speedup_score
# 综合得分
composite_score = (quality_weight * quality_score +
efficiency_weight * efficiency_score)
return {
'k': k,
'compression_ratio': compression_ratio,
'energy_preserved': energy_preserved,
'speedup_ratio': speedup_ratio,
'quality_score': quality_score,
'efficiency_score': efficiency_score,
'composite_score': composite_score
}
# 测试多个k值
test_ks = [10, 20, 32, 45, 60, 78, 100, 112, 140, 187]
results = []
print("综合评分分析:")
print("k值 | 压缩率 | 能量保留 | 加速比 | 质量分 | 效率分 | 综合分")
print("-" * 75)
for k in test_ks:
if k > len(s): continue
result = compute_composite_score(k, m, n, cumulative_energy, params_original)
results.append(result)
print(f"{k:3d} | {result['compression_ratio']:+.2%} | {result['energy_preserved']:7.3%} | "
f"{result['speedup_ratio']:5.2f}x | {result['quality_score']:6.3f} | "
f"{result['efficiency_score']:6.3f} | {result['composite_score']:6.3f}")
# 找到综合评分最高的k值
best_result = max(results, key=lambda x: x['composite_score'])
best_k = best_result['k']
print(f"\n 最优k值分析:")
print(f"最优选择: k = {best_k}")
print(f"综合评分: {best_result['composite_score']:.3f}")
print(f"压缩率: {best_result['compression_ratio']:+.2%}")
print(f"能量保留: {best_result['energy_preserved']:.3%}")
print(f"计算加速: {best_result['speedup_ratio']:.2f}×")
print(f"参数变化: {params_original:,} → {m*best_k + best_k*n:,}")
# 验证这是否是合理的工程选择
if best_result['compression_ratio'] > 0.5 and best_result['energy_preserved'] > 0.8:
print(" 工程可行性: 优秀 - 高压缩且质量良好")
elif best_result['compression_ratio'] > 0.3 and best_result['energy_preserved'] > 0.85:
print(" 工程可行性: 良好 - 平衡的压缩与质量")
else:
print(" 工程可行性: 需要重新评估权衡")
# 创建最终压缩版本
k_final = 32
U_final = U[:, :k_final]
s_final = s[:k_final]
Vt_final = Vt[:k_final, :]
# 构建压缩矩阵
B = U_final @ np.diag(s_final) # 500 × 60
C = Vt_final # 60 × 300
# 重构近似矩阵
approx_final = B @ C
print("最终选择: k = 32")
print("=" * 50)
print("压缩配置:")
print(f" • 原始: W ({m}×{n}) = {m*n:,} 参数")
print(f" • 压缩: B ({m}×{k_final}) + C ({k_final}×{n}) = {m*k_final + k_final*n:,} 参数")
print(f" • 参数减少: {m*n - (m*k_final + k_final*n):,}")
print("\n性能指标:")
print(f" • 压缩率: {1 - (m*k_final + k_final*n)/(m*n):+.2%}")
print(f" • 存储节省: {(m*n*4 - (m*k_final + k_final*n)*4)/1024:.1f} KB")
print(f" • 能量保留: {cumulative_energy[k_final-1]:.3%}")
print(f" • 近似误差: {np.linalg.norm(original_matrix - approx_final)/np.linalg.norm(original_matrix):.3%}")
print(f" • 计算加速: {(m*n)/(m*k_final + k_final*n):.2f}×")输出结果:
原始矩阵: 500 × 300 = 150,000 参数
矩阵Frobenius范数: 2099.51
SVD分解完成!
奇异值数量: 300
前10个奇异值: [516.47922384 502.2244437 491.92698647 474.29267731 459.52906406
454.10326343 446.45609874 432.98211643 426.46331753 424.09135519]
奇异值总和: 11819.41
总能量: 4407928.42
前10个奇异值的能量贡献:
奇异值1: 516.48 → 贡献: 6.052%
奇异值2: 502.22 → 贡献: 5.722%
奇异值3: 491.93 → 贡献: 5.490%
奇异值4: 474.29 → 贡献: 5.103%
奇异值5: 459.53 → 贡献: 4.791%
奇异值6: 454.10 → 贡献: 4.678%
奇异值7: 446.46 → 贡献: 4.522%
奇异值8: 432.98 → 贡献: 4.253%
奇异值9: 426.46 → 贡献: 4.126%
奇异值10: 424.09 → 贡献: 4.080%
理论最大压缩秩计算:
原始参数: 500 × 300 = 150,000
压缩参数: 500 × k + k × 300 = 800 × k
压缩条件: 800 × k < 150000
解得: k < 150000 / 800 = 187
临界点验证 (k=187):
原始参数: 150,000
压缩参数: 149,600
压缩率: +0.2667%
临界点附近的压缩效果:
k值 | 压缩参数 | 压缩率 | 状态
185 | 148,000 | +1.3333% | 压缩
186 | 148,800 | +0.8000% | 压缩
187 | 149,600 | +0.2667% | 压缩
188 | 150,400 | -0.2667% | 膨胀
189 | 151,200 | -0.8000% | 膨胀
190 | 152,000 | -1.3333% | 膨胀
基于能量保留的k值选择:
目标能量 | 所需k值 | 压缩率 | 能量实际值
70% | 17 | +90.93% | 72.094%
80% | 20 | +89.33% | 80.263%
90% | 25 | +86.67% | 91.488%
95% | 27 | +85.60% | 95.303%
k=32 详细分析 (70%能量目标):
• 参数: 500×17 + 17×300 = 13,600
• 压缩率: +90.93%
• 能量保留: 72.094%
• 近似误差: 52.826%
• 计算加速: 11.03×
k=45 详细分析 (80%能量目标):
• 参数: 16,000
• 压缩率: +89.33%
• 能量保留: 80.263%
• 近似误差: 44.427%
• 计算加速: 9.38×
综合评分分析:
k值 | 压缩率 | 能量保留 | 加速比 | 质量分 | 效率分 | 综合分
10 | +94.67% | 48.817% | 18.75x | 0.488 | 0.963 | 0.678
20 | +89.33% | 80.263% | 9.38x | 0.803 | 0.925 | 0.852
32 | +82.93% | 99.972% | 5.86x | 1.000 | 0.869 | 0.948
45 | +76.00% | 99.976% | 4.17x | 1.000 | 0.778 | 0.911
60 | +68.00% | 99.979% | 3.12x | 1.000 | 0.689 | 0.875
78 | +58.40% | 99.983% | 2.40x | 1.000 | 0.593 | 0.837
100 | +46.67% | 99.987% | 1.88x | 1.000 | 0.485 | 0.794
112 | +40.27% | 99.989% | 1.67x | 1.000 | 0.429 | 0.772
140 | +25.33% | 99.992% | 1.34x | 1.000 | 0.305 | 0.722
187 | +0.27% | 99.996% | 1.00x | 1.000 | 0.106 | 0.642
最优k值分析:
最优选择: k = 32
综合评分: 0.948
压缩率: +82.93%
能量保留: 99.972%
计算加速: 5.86×
参数变化: 150,000 → 25,600
工程可行性: 优秀 - 高压缩且质量良好
最终选择: k = 32
==================================================
压缩配置:
• 原始: W (500×300) = 150,000 参数
• 压缩: B (500×32) + C (32×300) = 25,600 参数
• 参数减少: 124,400
性能指标:
• 压缩率: +82.93%
• 存储节省: 485.9 KB
• 能量保留: 99.972%
• 近似误差: 1.676%
• 计算加速: 5.86×
本例的核心发现
对于500×300的矩阵:
理论临界:k < 187
推荐选择:k = 32
达成效果:82%压缩率 + 99%质量保留 + 5.86倍加速
这个选择在压缩率、质量保留和计算效率之间取得了最佳平衡,是经过严格数学计算和工程权衡后的最优解。
七、总结
SVD模型压缩是一项兼具理论深度和实践价值的技术。通过科学地选择K值,我们可以在精度损失和压缩收益之间找到最佳平衡点,成功的压缩不是简单地减少参数,而是在保持模型性能的前提下,实现存储、计算、能耗的全面优化。这需要深入理解模型结构、数据特性和应用需求。