算法专题十九：记忆化搜索（暴搜-＞记忆化搜索）

什么是记忆化搜索，就是在规律中找出完全一模一样的进行存储，当搜索到这种情况时候，之间从存储的情况中返回

斐波那契数

解法一：递归

java 复制代码

class Solution {
    public int fib(int n) {
        return dfs(n);
    }

    public int dfs(int n){
        if(n==0 || n==1){
            return n;
        }
        return dfs(n-1)+dfs(n-2);
    }
}

解法二：记忆化搜索

java 复制代码

class Solution {
    int[] memo;
    public int fib(int n) {
        memo=new int[32];
        Arrays.fill(memo,-1);
        return dfs(n);
        
    }

    public int dfs(int n){
        if(memo[n]!=-1){
            return memo[n];
        }
        if(n==0 || n==1){
            return n;
        }
        memo[n]=dfs(n-1)+dfs(n-2);
        return memo[n];
    }
}

解法三：动态规划

java 复制代码

class Solution {
    int[] dp;
    public int fib(int n) {
        dp=new int[31];
        dp[0]=0;
        dp[1]=1;
        for(int i=2;i<=n;i++){
            dp[i]=dp[i-1]+dp[i-2];
        }
        return dp[n];
    }
}

不同路径

62. 不同路径 - 力扣（LeetCode）

直接递归的话，会超出时间的限制

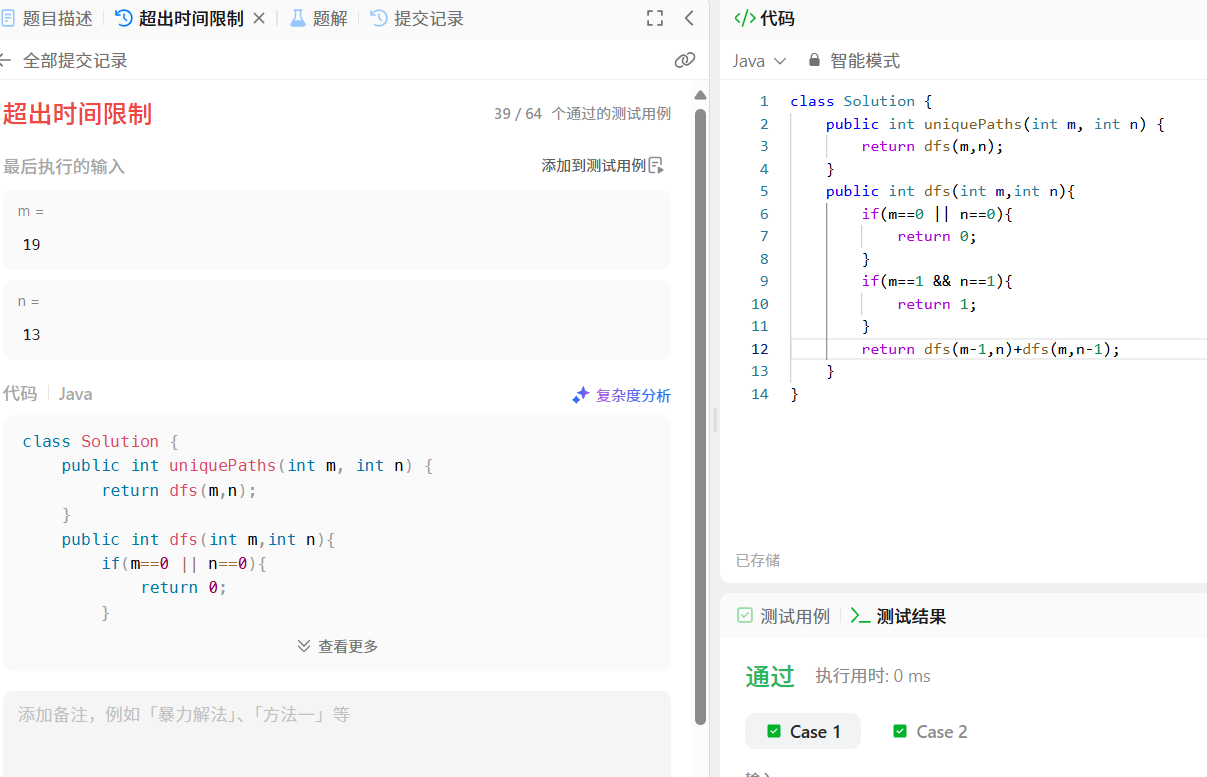
使用记忆化搜索的方式

java 复制代码

class Solution {
    int[][] memo;
    public int uniquePaths(int m, int n) {
        memo=new int[m+1][n+1];
        return dfs(m,n);
        
    }
    public int dfs(int m,int n){
        if(memo[m][n]!=0){
            return memo[m][n];
        }
        if(m==0 || n==0){
            return 0;
        }
        if(m==1 && n==1){
            memo[m][n]=1;
            return 1;
        }
        memo[m][n]=dfs(m-1,n)+dfs(m,n-1);
        return memo[m][n];
    }
}

使用动态规划

java 复制代码

class Solution {
    int[][] dp;
    public int uniquePaths(int m, int n) {
        dp=new int[m+1][n+1];
        dp[1][1]=1;
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                if(i==1 && j==1){
                    continue;
                }
                dp[i][j]=dp[i][j-1]+dp[i-1][j];
            }
        }
        return dp[m][n];
    }
}

最长递增子序列

300. 最长递增子序列 - 力扣（LeetCode）

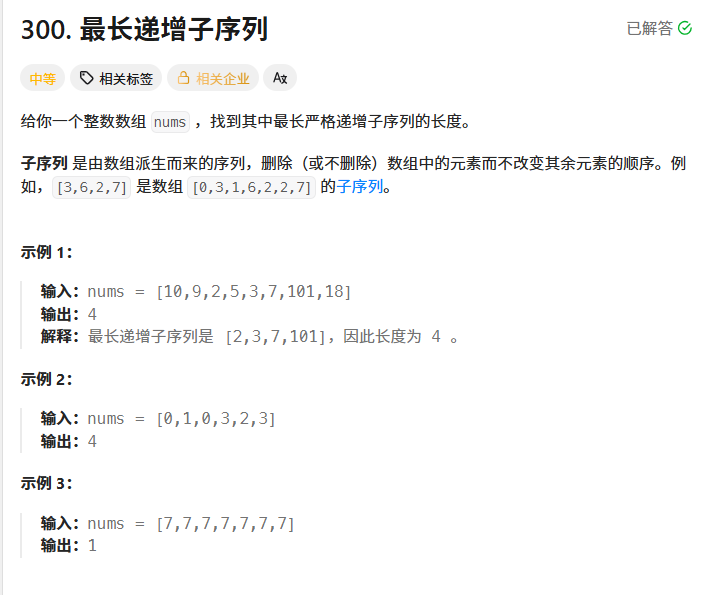
直接使用递归会超时

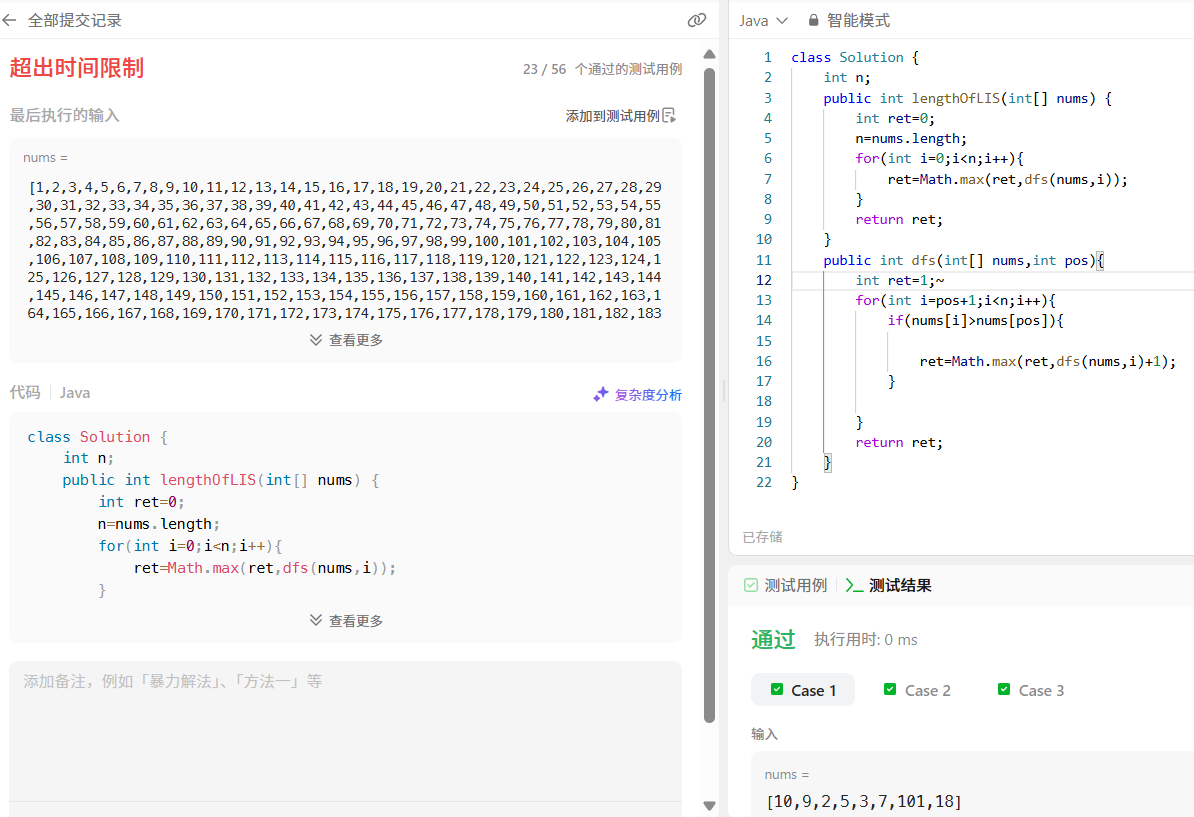
使用记忆化搜索

java 复制代码

class Solution {
    int n;
    int[] memo;
    public int lengthOfLIS(int[] nums) {
        int ret=0;
        n=nums.length;
        memo=new int[n];
        for(int i=0;i<n;i++){
            ret=Math.max(ret,dfs(nums,i,memo));
        }
        return ret;
    }
    public int dfs(int[] nums,int pos,int[] memo){
        if(memo[pos]!=0){
            return memo[pos];
        }
        int ret=1;
        for(int i=pos+1;i<n;i++){
            if(nums[i]>nums[pos]){
                
                ret=Math.max(ret,dfs(nums,i,memo)+1);
            }
            
        }
        memo[pos]=ret;
        return ret;
    }
}

使用动态规划

java 复制代码

class Solution {
    public int lengthOfLIS(int[] nums) {
        int n=nums.length;
        int[] dp=new int[n];
        int ret=0;
        Arrays.fill(dp,1);
        for(int i=n-1;i>=0;i--){
            for(int j=i+1;j<n;j++){
                if(nums[i]<nums[j]){
                    dp[i]=Math.max(dp[i],dp[j]+1);
                }
            }
            ret=Math.max(ret,dp[i]);
        }
        return ret;
        
    }
}

猜数字的大小Ⅱ

375. 猜数字大小 II - 力扣（LeetCode）

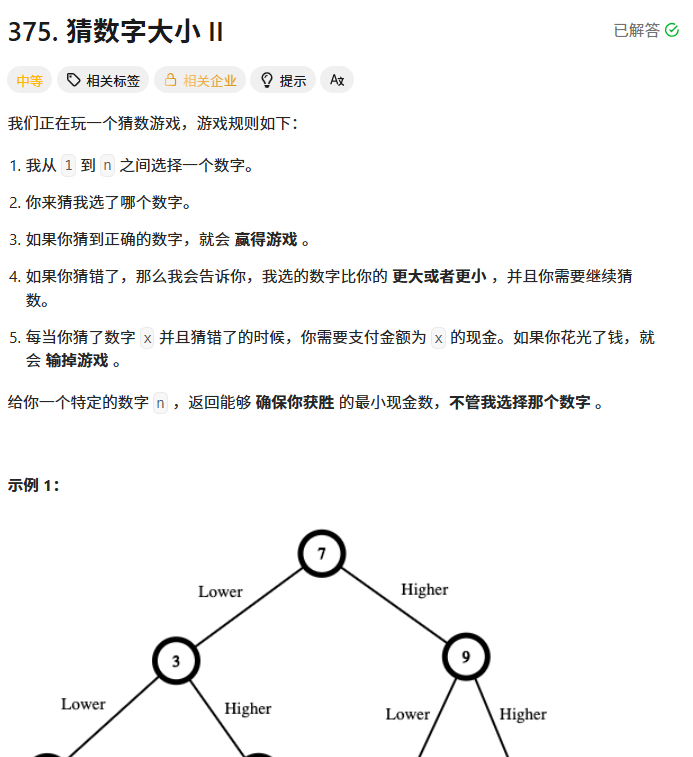
暴搜会超出时间的限制

利用记忆化搜索

取最大值的意思就是最坏情况（保证所有情况都能猜到10的前提下），然后在所有能猜中10的情况下找出最小值

java 复制代码

class Solution {
    int[][] memo;
    public int getMoneyAmount(int n) {
        memo=new int[n+1][n+1];
        return dfs(1,n);
    }
    public int dfs(int left,int right){

        int ret=Integer.MAX_VALUE;
        if(left>=right){
            return 0;
        }
        if(memo[left][right]!=0){
            return memo[left][right];
        }
        for(int head=left;head<=right;head++){
            int x=dfs(left,head-1);
            int y=dfs(head+1,right);
            ret=Math.min(Math.max(x,y)+head,ret);
        }
        memo[left][right]=ret;
        return ret;
    }
}

矩阵中的最长递增路径

329. 矩阵中的最长递增路径 - 力扣（LeetCode）

直接暴搜会超时

使用记忆化搜索

java 复制代码

class Solution {
    int[] dx={0,0,-1,1};
    int[] dy={1,-1,0,0};
    int[][] memo;
    int m,n;
    public int longestIncreasingPath(int[][] matrix) {
        m=matrix.length;
        n=matrix[0].length;
        memo=new int[m][n];
        int ret=0;
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                ret=Math.max(ret,dfs(matrix,i,j,memo));
            }
        }
        return ret;
    }

    public int dfs(int[][] ma,int i,int j,int[][] memo){
        if(memo[i][j]!=0){
            return memo[i][j];
        }
        int ret=1;
        for(int k=0;k<4;k++){
            int x=i+dx[k];
            int y=j+dy[k];
            if(x>=0 && x<m && y>=0 && y<n && ma[x][y]>ma[i][j]){
                ret=Math.max(ret,dfs(ma,x,y,memo)+1);
            }
        }
        memo[i][j]=ret;
        return ret;
    }
}