《算法通关指南数据结构和算法篇（2）--- 链表专题》

《不一样的数据结构之--- 链表》

---

🔥小龙报：个人主页

🎬作者简介：C++研发，嵌入式，机器人方向学习者

❄️个人专栏：《C语言》《算法通关指南》
✨ 永远相信美好的事情即将发生

文章目录

• 《不一样的数据结构之--- 链表》
• 前言
• 一、链表的概念
• • 1.1 链表的定义
  • 1.2 链表的分类
• 二、链表的模拟实现
• • 2.1 单链表的模拟实现
  • • 2.1.1 定义-创建-初始化
    • 2.1.2 头插
    • 2.1.3 遍历链表
    • 2.1.4 按值查找
    • • 策略一：遍历整个链表
      • 策略二：使用哈希表优化
    • 2.1.5 在任意位置之后插入元素
    • 2.1.6 删除任意位置之后的元素
    • 2.1.7 遗留问题
    • 2.1.8 所有测试代码
  • 2.2 双向链表的模拟实现
  • • 2.2.1 实现方式
    • 2.2.2 定义
    • 2.2.3 头插
    • 2.2.4 遍历链表
    • 2.2.5 按值查找
    • 2.2.6 在任意位置之后插入元素
    • 2.2.7 在任意位置之前插入元素
    • 2.2.8 删除任意位置的元素
    • 2.2.9 所有测试代码
  • 2.3 循环链表的模拟实现
• 三、总结与每日励志

---

前言

本系列讲解算法竞赛的数据结构在算法竞赛中，我们主要关心的其实是时间开销，空间上是基本够用的，因此我们是使用庞大的数组实现的话不多说冲！

一、链表的概念

1.1 链表的定义

线性表的链式存储就是链表 。它是将元素存储在物理上任意的存储单元中，由于无法像顺序表⼀样通过下标保证数据元素之间的逻

辑关系，链式存储除了要保存数据元素外，还需额外维护数据元素之间的逻辑关系，这两部分信息合称结点（node）。即结点有两个域：保存数据元素的数据域和存储逻辑关系的指针域。

1.2 链表的分类

二、链表的模拟实现

2.1 单链表的模拟实现

2.1.1 定义-创建-初始化

（1） 两个足够大的数组，⼀个用来存数据，一个用来存下⼀个结点的位置

（2） 变量h ，充当头指针，表示头结点的位置

（3） 变量id，为新来的结点分位置

const int N = 1e5 + 10;
int h; //头指针
int id; // 下⼀个元素分配的位置
int e[N], ne[N]; // 数据域和指针域

// 下标0位置作为哨兵位
// 其中ne数组全部初始化为0，其中ne[i] = 0就表⽰空指针，后续没有结点
// 当然，也可以初始化为- 1作为空指针，看个⼈爱好

2.1.2 头插

void push_front(int x)
{
	id++;
	e[id] = x;

	// 1. x 的右指针指向哨兵位的后继
    // 2. 哨兵位的右指针指向
	ne[id] = ne[h];
	ne[h] = id;
}

时间复杂度：O(1)

2.1.3 遍历链表

//遍历链表
void print()
{
	for (int i = ne[0]; i; i = ne[i])
	{
		cout << e[i] << endl;
	}
}

时间复杂度：O(1)

2.1.4 按值查找

策略一：遍历整个链表

int find(int x)
{
	for (int i = ne[0]; i; i = ne[i])
	{
		if (e[i] == x)
			return i;
	}
	return 0;
}

时间复杂度：O(N)

策略二：使用哈希表优化

int find(int x)
{
	return mp[x];
}

时间复杂度：O(1)

2.1.5 在任意位置之后插入元素

void insert(int p, int x) // ⼀定要注意，这⾥的p是位置，不是元素
{
	id++;
	e[id] = x;

	ne[id] = ne[p];  // x 指向p的后⾯
	ne[p] = id;   // p 指向x
}

时间复杂度：O(1)

2.1.6 删除任意位置之后的元素

void erase(int p)
{
	if (ne[p])
	{
		mp[e[ne[p]]] = 0;   // 将p后⾯的元素从mp中删除
		ne[p] = ne[ne[p]];  //指向下⼀个元素的下⼀个元素

	}
}

时间复杂度：O(1)

2.1.7 遗留问题

为什么不像顺序表⼀样，实现⼀个尾插、尾删、删除任意位置的元素等操作？

答：能实现，但是没必要。因为时间复杂度是O(N)级别的。

使用各种数据结构是⽅便我们去解决问题的，⽽不是添堵（增加时间复杂度）的

2.1.8 所有测试代码

#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int h; //头指针
int id; // 下⼀个元素分配的位置
int e[N], ne[N]; // 数据域和指针域
int mp[N]; // mp[i] 表⽰i在这个元素存放的位置

//头插
void push_front(int x)
{
	id++;
	e[id] = x;

	// 1. x 的右指针指向哨兵位的后继
    // 2. 哨兵位的右指针指向
	ne[id] = ne[h];
	ne[h] = id;
	mp[x] = id;
}

//遍历链表
void print()
{
	for (int i = ne[0]; i; i = ne[i])
	{
		cout << e[i] << " ";
	}
	cout << endl << endl;

}

// 按值查找
int find(int x)
{
	return mp[x];
}

//在任意位置之后插⼊元素
void insert(int p, int x) // ⼀定要注意，这⾥的p是位置，不是元素
{
	id++;
	e[id] = x;

	ne[id] = ne[p];  // x 指向p的后⾯
	ne[p] = id;   // p 指向x

}

//删除存储位置为p后⾯的元素
void erase(int p)
{
	if (ne[p])
	{
		mp[e[ne[p]]] = 0;   // 将p后⾯的元素从mp中删除
		ne[p] = ne[ne[p]];  //指向下⼀个元素的下⼀个元素

	}
}

int main()
{
	for (int i = 1; i <= 5; i++)
	{
		push_front(i);
		print();
	}
	//cout << find(1) << endl;
	//cout << find(5) << endl;
	//cout << find(6) << endl;
	// insert(1, 10);
	// print();
	// insert(2, 100);
	// print();
	/*erase(2);
	print();
	erase(4);
	print();*/
	return 0;
}

运行结果：

2.2 双向链表的模拟实现

2.2.1 实现方式

双向链表无非就是在单链表的基础上加上⼀个指向前驱的指针，那就 再来⼀个数组充当指向前驱的指针域 即可

2.2.2 定义

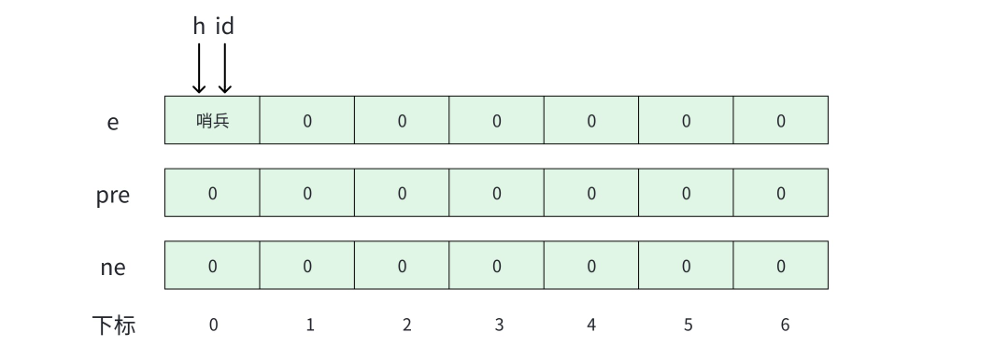
const int N = 1e5 + 10;
int h; // 头结点
int id; // 下⼀个元素分配的位置
int e[N]; // 数据域
int pre[N], ne[N]; // 前后指针域

2.2.3 头插

//头插
void push_front(int x)
{
	id++;
	e[id] = x;

	pre[id] = h;
	ne[id] = ne[h];
	pre[ne[h]] = id;
	ne[h] = id;
}

时间复杂度：O(1)

2.2.4 遍历链表

直接无视prev 数组，与单链表的遍历方式一致。

void print()
{
	for (int i = ne[0]; i; i = ne[i])
	{
		cout << e[i] << " ";
	}
	cout << endl << endl;

}

时间复杂度：O(1)

2.2.5 按值查找

直接使用哈希表的思想进行优化

int find(int x)
{
	return mp[x];
}

时间复杂度：O(1)

2.2.6 在任意位置之后插入元素

void insert_back(int p, int x)
{
	id++;
	e[id] = x;

	pre[id] = p;
	ne[id] = ne[p];

	// 先让p的后继的左指针指向id
	// 再让p的右指针指向id
	pre[ne[p]] = id;
	ne[p] = id;
}

时间复杂度：O(1)

2.2.7 在任意位置之前插入元素

void insert_front(int p, int x)
{
	id++;
	e[id] = x;

	pre[id] = pre[p];
	ne[id] = p;

	// 先让p的前驱的右指针指向id
	// 再让p的左指针指向id
	ne[pre[p]] = id;
	pre[p] = id;
}

时间复杂度：O(1)

2.2.8 删除任意位置的元素

void erase(int p)
{
	ne[pre[p]] = ne[p];
	pre[ne[p]] = pre[p];
}

时间复杂度：O(1)

2.2.9 所有测试代码

#include <iostream>
using namespace std;

const int N = 1e5 + 10;
int h; // 头结点
int id; // 下⼀个元素分配的位置
int e[N]; // 数据域
int pre[N], ne[N]; // 前后指针域
int mp[N]; //mp[i] 表⽰i在这个元素存放的位置

//头插
void push_front(int x)
{
	id++;
	e[id] = x;

	pre[id] = h;
	ne[id] = ne[h];
	pre[ne[h]] = id;
	ne[h] = id;
	mp[x] = id;
}


//遍历链表
void print()
{
	for (int i = ne[0]; i; i = ne[i])
	{
		cout << e[i] << " ";
	}
	cout << endl << endl;

}

// 按值查找
int find(int x)
{
	return mp[x];
}

// 在存储位置为p的元素后⾯，插⼊⼀个元素x
void insert_back(int p, int x)
{
	id++;
	e[id] = x;

	pre[id] = p;
	ne[id] = ne[p];

	// 先让p的后继的左指针指向id
	// 再让p的右指针指向id
	pre[ne[p]] = id;
	ne[p] = id;
}

//在任意位置之前插入元素
void insert_front(int p, int x)
{
	id++;
	e[id] = x;

	pre[id] = pre[p];
	ne[id] = p;

	// 先让p的前驱的右指针指向id
	// 再让p的左指针指向id
	ne[pre[p]] = id;
	pre[p] = id;
}

// 删除任意位置p的元素
void erase(int p)
{
	ne[pre[p]] = ne[p];
	pre[ne[p]] = pre[p];
}
int main()
{
	for (int i = 1; i <= 8; i++)
	{
		push_front(i);
		print();
	}
	//cout << find(3) << endl;
	//cout << find(5) << endl;
	//cout << find(0) << endl;
	// insert_front(2, 22);
	// print();
	// insert_front(3, 33);
	// print();
	// insert_front(4, 44);
	// print();
	//erase(2);
	//print();
	//erase(4);
	//print();
	return 0;
}

运行结果：

2.3 循环链表的模拟实现

回看之前实现的带头单向链表。我们定义 表示空指针，但其实哨兵位就在 位置，所有的结构正好成环

三、总结与每日励志

✨ ***本文介绍了链表这一重要的数据结构，重点讲解了单链表和双向链表的实现方法。作者通过数组模拟链表的方式，详细展示了链表的定义、初始化以及常见操作（头插、遍历、查找、插入和删除）的实现代码与时间复杂度分析。单链表使用两个数组分别存储数据和指针，双向链表则增加前驱指针数组。文章特别强调了哈希表在优化查找效率中的应用，并对比了不同操作的时间复杂度。通过实际代码示例，读者可以清晰理解链表的底层实现逻辑及其在算法竞赛中的应用优势。***