数据结构 —— 栈

zz0723202025-11-05 19:43

栈是一种先进后出（LIFO, Last In First Out） 的线性数据结构，它只允许在一端（称为栈顶）进行插入和删除操作。栈的特性使其在很多场景中发挥重要作用，如表达式求值、函数调用、括号匹配、深度优先搜索等。本文将详细讲解栈的概念、实现及应用。

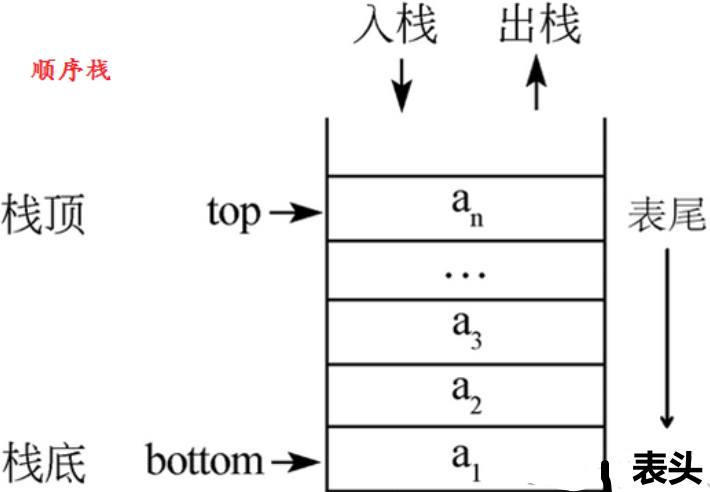
1.栈的基本概念

核心术语

  • 栈顶（Top）：允许插入和删除操作的一端
  • 栈底（Bottom）：固定的，不允许操作的一端
  • 压栈（Push）：在栈顶插入元素的操作
  • 弹栈（Pop）：从栈顶删除元素的操作
  • 栈空（Empty）：栈中没有任何元素的状态
  • 栈满（Full）：栈中元素达到最大容量的状态

栈的特性

  • 元素的插入和删除只能在栈顶进行；
  • 元素的访问顺序是 "先进后出"，最后进入的元素最先被访问；
  • 栈是一种操作受限的线性表。

栈的基本操作

  • push(element)：向栈顶插入元素
  • pop()：移除并返回栈顶元素
  • peek()：返回栈顶元素但不移除
  • isEmpty()：判断栈是否为空
  • isFull()：判断栈是否已满（仅数组实现）
  • size()：返回栈中元素个数
  • clear()：清空栈中所有元素

2.栈的两种实现方式

一、基于数组实现

数组实现的栈使用固定大小的数组存储元素，实现简单但容量固定。

java 复制代码 
import java.util.EmptyStackException;

/**
 * 基于数组的栈实现
 * @param <T> 栈中元素的类型
 */
public class ArrayStack<T> {
    private T[] stack;    // 存储栈元素的数组
    private int top;      // 栈顶指针，指向栈顶元素的索引
    private int capacity; // 栈的容量

    // 构造指定容量的栈
    @SuppressWarnings("unchecked")
    public ArrayStack(int capacity) {
        this.capacity = capacity;
        stack = (T[]) new Object[capacity];
        top = -1; // 栈空时，栈顶指针为-1
    }

    // 构造默认容量为10的栈
    public ArrayStack() {
        this(10);
    }

    /**
             * 压栈操作：向栈顶添加元素
             * @param element 要添加的元素
             * @throws StackOverflowError 如果栈已满
             */
    public void push(T element) {
        if (isFull()) {
            throw new StackOverflowError("栈已满，无法添加元素");
        }
        stack[++top] = element; // 先移动栈顶指针，再添加元素
    }

    /**
             * 弹栈操作：移除并返回栈顶元素
             * @return 栈顶元素
             * @throws EmptyStackException 如果栈为空
             */
    public T pop() {
        if (isEmpty()) {
            throw new EmptyStackException();
        }
        T element = stack[top];
        stack[top--] = null; // 帮助垃圾回收
        return element;
    }

    /**
             * 获取栈顶元素但不移除
             * @return 栈顶元素
             * @throws EmptyStackException 如果栈为空
             */
    public T peek() {
        if (isEmpty()) {
            throw new EmptyStackException();
        }
        return stack[top];
    }

    /**
             * 判断栈是否为空
             * @return 如果栈为空返回true，否则返回false
             */
    public boolean isEmpty() {
        return top == -1;
    }

    /**
             * 判断栈是否已满
             * @return 如果栈已满返回true，否则返回false
             */
    public boolean isFull() {
        return top == capacity - 1;
    }

    /**
             * 获取栈中元素的个数
             * @return 栈中元素的个数
             */
    public int size() {
        return top + 1;
    }

    /**
             * 清空栈
             */
    public void clear() {
        // 清空元素，帮助垃圾回收
        for (int i = 0; i <= top; i++) {
            stack[i] = null;
        }
        top = -1;
    }

    /**
             * 打印栈中的元素
             */
    public void printStack() {
        if (isEmpty()) {
            System.out.println("栈为空");
            return;
        }
        System.out.print("栈元素（从栈底到栈顶）：");
        for (int i = 0; i <= top; i++) {
            System.out.print(stack[i] + " ");
        }
        System.out.println();
    }

    public static void main(String[] args) {
    ArrayStack<Integer> stack = new ArrayStack<>(5);

    // 压栈
    stack.push(1);
    stack.push(2);
    stack.push(3);
    stack.printStack(); // 输出: 栈元素（从栈底到栈顶）：1 2 3

    // 查看栈顶元素
    System.out.println("栈顶元素: " + stack.peek()); // 输出: 3

    // 弹栈
    System.out.println("弹出元素: " + stack.pop()); // 输出: 3
    stack.printStack(); // 输出: 栈元素（从栈底到栈顶）：1 2

    // 栈大小
    System.out.println("栈大小: " + stack.size()); // 输出: 2

    // 继续压栈
    stack.push(4);
    stack.push(5);
    stack.push(6);
    stack.printStack(); // 输出: 栈元素（从栈底到栈顶）：1 2 4 5 6

    // 测试栈满
    try {
    stack.push(7);
    } catch (StackOverflowError e) {
    System.out.println(e.getMessage()); // 输出: 栈已满，无法添加元素
    }

    // 清空栈
    stack.clear();
    System.out.println("栈是否为空: " + stack.isEmpty()); // 输出: true
    }
    }

二、基于链表的栈实现

链栈是一种基于链表实现的栈，其特点是无需事先分配固定长度的存储空间，栈的长度可以动态增长或缩小，避免了顺序栈可能存在的空间浪费和存储溢出问题。

链栈中的每个元素称为"节点"，每个节点包括两个部分：数据域和指针域。数据域用来存储栈中的元素值，指针域用来指向栈顶元素所在的节点。

链栈的基本操作包括入栈、出栈、获取栈顶元素和遍历等，相比顺序栈而言，链栈的实现难度稍高，但其在某些情况下有着更好的灵活性和效率，特别适用于在动态存储空间较为紧缺的场合。

注意：如果栈的使用过程中元素变化不可预料,那么最好使用链栈,反之,如果它的变化在可控范围内,建议使用顺序栈。

链栈可以分为单链栈和双链栈：

单链栈使用单链表实现，每个节点只含有一个指向下一个节点的指针。因此，单链栈只能从栈顶进行插入和删除操作。

双链栈使用双向链表实现，每个节点同时包含指向前一个节点和后一个节点的指针。因此，双链栈既可以从栈顶进行插入和删除操作，也可以从栈底进行插入和删除操作，使得操作更加灵活。

java 复制代码 
import java.util.EmptyStackException;

/**
 * 基于链表的栈实现
 * @param <T> 栈中元素的类型
 */
public class LinkedStack<T> {
    // 节点类
    private static class Node<T> {
        T data;       // 节点数据
        Node<T> next; // 指向下一个节点的引用

        public Node(T data) {
            this.data = data;
            this.next = null;
        }
    }

    private Node<T> top;  // 栈顶节点
    private int size;     // 栈中元素的个数

    // 构造空栈
    public LinkedStack() {
        top = null;
        size = 0;
    }

    /**
             * 压栈操作：向栈顶添加元素
             * @param element 要添加的元素
             */
    public void push(T element) {
        Node<T> newNode = new Node<>(element);
        newNode.next = top; // 新节点指向当前栈顶
        top = newNode;      // 更新栈顶为新节点
        size++;
    }

    /**
             * 弹栈操作：移除并返回栈顶元素
             * @return 栈顶元素
             * @throws EmptyStackException 如果栈为空
             */
    public T pop() {
        if (isEmpty()) {
            throw new EmptyStackException();
        }
        T data = top.data;
        top = top.next; // 更新栈顶为下一个节点
        size--;
        return data;
    }

    /**
             * 获取栈顶元素但不移除
             * @return 栈顶元素
             * @throws EmptyStackException 如果栈为空
             */
    public T peek() {
        if (isEmpty()) {
            throw new EmptyStackException();
        }
        return top.data;
    }

    /**
             * 判断栈是否为空
             * @return 如果栈为空返回true，否则返回false
             */
    public boolean isEmpty() {
        return top == null;
    }

    /**
             * 获取栈中元素的个数
             * @return 栈中元素的个数
             */
    public int size() {
        return size;
    }

    /**
             * 清空栈
             */
    public void clear() {
        top = null;
        size = 0;
    }

    /**
             * 打印栈中的元素
             */
    public void printStack() {
        if (isEmpty()) {
            System.out.println("栈为空");
            return;
        }
        System.out.print("栈元素（从栈顶到栈底）：");
        Node<T> current = top;
        while (current != null) {
            System.out.print(current.data + " ");
            current = current.next;
        }
        System.out.println();
    }

    public static void main(String[] args) {
        LinkedStack<String> stack = new LinkedStack<>();

        // 压栈
        stack.push("A");
        stack.push("B");
        stack.push("C");
        stack.printStack(); // 输出: 栈元素（从栈顶到栈底）：C B A

    // 查看栈顶元素
    System.out.println("栈顶元素: " + stack.peek()); // 输出: C

    // 弹栈
    System.out.println("弹出元素: " + stack.pop()); // 输出: C
    stack.printStack(); // 输出: 栈元素（从栈顶到栈底）：B A

    // 栈大小
    System.out.println("栈大小: " + stack.size()); // 输出: 2

    // 继续压栈
    stack.push("D");
    stack.push("E");
    stack.printStack(); // 输出: 栈元素（从栈顶到栈底）：E D B A

    // 清空栈
    stack.clear();
    System.out.println("栈是否为空: " + stack.isEmpty()); // 输出: true
    }
    }

三、两种实现方式的对比

|----------|---------------|-----------------|--------------|--------------|
| 实现方式 | 优点 | 缺点 | 时间复杂度 | 适用场景 |
| 数组实现 | 实现简单访问速度快内存连续 | 容量固定，可能溢出扩容成本高 | 所有操作都是 O (1) | 已知最大容量对性能要求高 |
| 链表实现 | 容量动态扩展没有溢出问题 | 实现较复杂需要额外空间存储指针 | 所有操作都是 O (1) | 未知最大容量需要灵活扩展 |

3.java 中栈的实现

Java 标准库中提供了java.util.Stack类，但该类是遗留类，继承自Vector，存在一些设计缺陷，不推荐使用。

推荐使用java.util.Deque接口的实现类作为栈使用，如ArrayDeque：

java 复制代码 
import java.util.Deque;
import java.util.ArrayDeque;

public class StackExample {
    public static void main(String[] args) {
        // 使用ArrayDeque作为栈
        Deque<Integer> stack = new ArrayDeque<>();
        
        // 压栈
        stack.push(1);
        stack.push(2);
        stack.push(3);
        
        // 查看栈顶元素
        System.out.println("栈顶元素: " + stack.peek()); // 输出: 3
        
        // 弹栈
        System.out.println("弹出元素: " + stack.pop()); // 输出: 3
        
        // 遍历栈
        System.out.print("栈元素: ");
        while (!stack.isEmpty()) {
            System.out.print(stack.pop() + " "); // 输出: 2 1
        }
    }
}

ArrayDeque作为栈使用的优势：

  • 性能优于Stack类
  • 接口设计更合理
  • 没有同步开销（Stack是线程安全的，带来额外开销）

4.栈的应用

1.函数递归调用

函数递归调用时，计算机会把函数调用时需要的参数和返回地址等信息放入栈中，函数执行完毕后再从栈中取回这些信息。

以汉诺塔为例：

java 复制代码 
public static void main(String[] args) {
    Hanoi(6,'A','B','C');
}

private static int count = 0;  //统计步数
//汉诺方法
public static void Hanoi(int n,char A,char B,char C){
    //当n为1时,直接移动
    if(n == 1){
        System.out.println("第"+ ++count + "步："+A +"-->"+C);
    } else {
        //当n不为1时
        //首先 为了将第n个盘子从A移到C  可先将第n-1个盘子借助C从A移到B
        Hanoi(n - 1, A, C, B);
        System.out.println("第" + ++count + "步：" + A + "-->" + C);
        //然后再将第n-1个盘子借助A从B移到C
        Hanoi(n - 1, B, A, C);
    }
}

2.括号匹配

java 复制代码 
public static void main(String[] args) {
    String expr1 = "((a + b) * (c - d))";
    String expr2 = "((a + b) * [c - d})";
    String expr3 = "a + b) * (c - d";

    System.out.println(expr1 + " 括号匹配: " + isBalanced(expr1)); // true
    System.out.println(expr2 + " 括号匹配: " + isBalanced(expr2)); // false
    System.out.println(expr3 + " 括号匹配: " + isBalanced(expr3)); // false
}
//检查括号匹配
public static boolean isBalanced(String expression){
Deque<Character> stack = new ArrayDeque<>();
for(char c : expression.toCharArray()){
    //如果是左括号，入栈
    if(c == '(' || c == '{' || c == '['){
        stack.push(c);
    }
        //如果是右括号
    else if(c == ')' || c == '}' || c == ']'){
        if(stack.isEmpty()){
            return false;
        }

        //弹出栈顶元素进行匹配
        char top = stack.pop();
        if(top == '(' && c != ')' || top == '{' && c != '}' || top == '[' && c!= ']'){
            return false;
        }
    }
}
return stack.isEmpty();
}

3.表达式求值

java 复制代码 
/**
 * 使用栈求后缀表达式（逆波兰表达式）的值
 */
public class ExpressionEvaluation {
    public static int evaluatePostfix(String[] tokens) {
        Deque<Integer> stack = new ArrayDeque<>();

        for (String token : tokens) {
            // 如果是运算符，弹出两个元素进行运算
            if (token.equals("+") || token.equals("-") ||
                token.equals("*") || token.equals("/")) {
                int b = stack.pop(); // 注意弹出顺序，后弹出的是第一个操作数
                int a = stack.pop();
                int result = 0;

                switch (token) {
                    case "+":
                        result = a + b;
                        break;
                    case "-":
                        result = a - b;
                        break;
                    case "*":
                        result = a * b;
                        break;
                    case "/":
                        result = a / b; // 假设除数不为0
                        break;
                }
                stack.push(result);
            }
                // 如果是数字，直接入栈
            else {
                stack.push(Integer.parseInt(token));
            }
        }

        return stack.pop();
    }

    public static void main(String[] args) {
        // 表达式: 3 + 4 * 2 / (1 - 5)
        // 后缀表达式: 3 4 2 * 1 5 - / +
        String[] tokens = {"3", "4", "2", "*", "1", "5", "-", "/", "+"};
        System.out.println("表达式结果: " + evaluatePostfix(tokens)); // 输出: 1
    }
}

4.浏览器历史记录

栈可以用于实现浏览器的前进和后退功能：

  • 访问新页面时，将当前页面压入历史栈
  • 点击后退按钮时，从历史栈弹出页面
  • 可以使用两个栈实现前进功能

5.栈性能的分析

栈的所有基本操作（push、pop、peek、isEmpty）的时间复杂度都是O(1)，因为这些操作只涉及栈顶元素，不需要遍历整个栈。

栈的空间复杂度是O(n)，其中 n 是栈中元素的数量，因为需要存储所有元素。

相关推荐
Madison-No72 小时前
【C++】关于list的使用&&底层实现
数据结构·c++·stl·list·模拟实现
Bug退退退1232 小时前
ArrayList 与 LinkedList 的区别
java·数据结构·算法
2301_807997384 小时前
代码随想录-day26
数据结构·c++·算法·leetcode
TL滕4 小时前
从0开始学算法——第一天（认识算法）
数据结构·笔记·学习·算法
代码雕刻家8 小时前
1.4.课设实验-数据结构-单链表-文教文化用品品牌2.0
c语言·数据结构
云边有个稻草人9 小时前
Rust 借用分割技巧：安全解构复杂数据结构
数据结构·安全·rust
侯小啾9 小时前
【22】C语言 - 二维数组详解
c语言·数据结构·算法
TL滕9 小时前
从0开始学算法——第一天（如何高效学习算法）
数据结构·笔记·学习·算法
yuuki23323310 小时前
【数据结构】双向链表的实现
c语言·数据结构·后端
热门推荐
01GitHub 镜像站点02综合整理：pdf预览显示：你尝试预览的文件可能对你的计算机有害。如果你信任此文件以及其来源，请打开此文件以看其内容，如何解决以正常预览文件03UV安装并设置国内源04npm使用国内淘宝镜像的方法05Linux下V2Ray安装配置指南06BongoCat - 跨平台键盘猫动画工具07《大数据技术原理与应用》实验报告三 熟悉HBase常用操作08NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南09安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）10GitLab 零基础入门指南：从安装到项目管理全流程