INT305 Machine Learning 机器学习 Pt.5 神经网络（Neural network）

文章目录

• [1. 神经网络（Neural network）](#1. 神经网络（Neural network）)
• • [1.1 激活函数（Activation Functions）](#1.1 激活函数（Activation Functions）)
  • [1.2 神经网络的架构](#1.2 神经网络的架构)
  • [1.3 神经网络的过程](#1.3 神经网络的过程)
  • • [1.3.1 链式法则（Chain Rule）](#1.3.1 链式法则（Chain Rule）)
    • • [1.3.1.1 三种基本节点的反向传播模式](#1.3.1.1 三种基本节点的反向传播模式)
      • [1.3.1.2 池化的反向传播](#1.3.1.2 池化的反向传播)
      • [1.3.1.3 向量时的梯度计算](#1.3.1.3 向量时的梯度计算)

1. 神经网络（Neural network）

这一部分知识在另一个功课里详细讨论了，这里讨论的神经网络是数学模型，而不是生物学上的大脑。

传统的线性模型： f = W x f=Wx f=Wx

这样的模型难以学习复杂的函数映射，因此有神经网络： f = W 2 m a x ( 0 , W 1 x ) f=W_2max(0,W_1x) f=W2max(0,W1x)(两层）

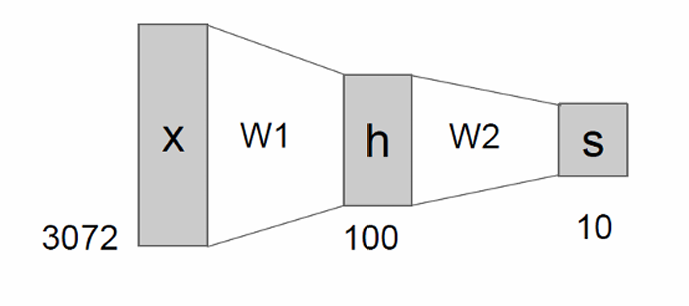
或者三层神经网络： f = W 3 m a x ( 0 , W 2 m a x ( 0 , W 1 x ) ) f=W_3max(0,W_2max(0,W_1x)) f=W3max(0,W2max(0,W1x))。

1.1 激活函数（Activation Functions）

神经网络里有多种激活函数（Activation Functions），我们快速带过：

1. Sigmoid: σ ( x ) = 1 1 + e − x \sigma(x) = \frac{1}{1 + e^{-x}} σ(x)=1+e−x1
   

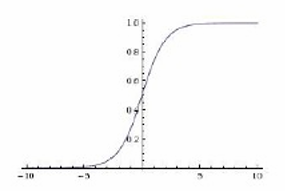
   S形曲线，输出值在0到1之间。

   平滑，输出值范围有限，但容易受到梯度消失问题的影响。

2. tanh： tanh ⁡ ( x ) \tanh(x) tanh(x)
   

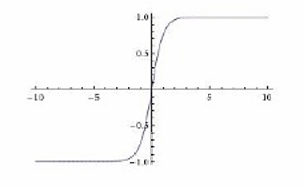
   S形曲线，输出值在-1到1之间。

   相对于Sigmoid，tanh的输出中心对称，但同样可能遇到梯度消失问题。

3. ReLU (Rectified Linear Unit)： max ⁡ ( 0 , x ) \max(0, x) max(0,x)
   

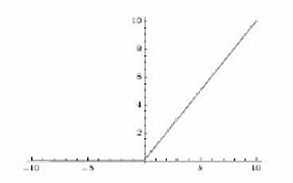
   在x=0处有一个转折点，x>0时输出为x，x<=0时输出为0。

   简单，计算效率高，有助于缓解梯度消失问题，但可能导致"死亡ReLU"问题（即神经元永久失活）。

4. Leaky ReLU： max ⁡ ( 0.1 x , x ) \max(0.1x, x) max(0.1x,x)
   

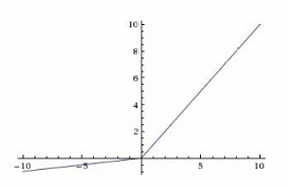
   在x<0时有一个小的斜率（0.1），x>=0时斜率为1。

   改进了ReLU，允许负值有一个小的梯度，有助于解决"死亡ReLU"问题。

5. Maxout： max ⁡ ( w 1 T x + b 1 , w 2 T x + b 2 ) \max(w_1^Tx + b_1, w_2^Tx + b_2) max(w1Tx+b1,w2Tx+b2)

   是一种通用的激活函数，可以看作是ReLU和Leaky ReLU的推广，通过选择两个线性函数的最大值来激活。

6. ELU (Exponential Linear Unit)：
   f ( x ) = { x if x > 0 α ( exp ⁡ ( x ) − 1 ) if x ≤ 0 f(x) = \begin{cases} x & \text{if } x > 0 \\ \alpha(\exp(x) - 1) & \text{if } x \leq 0 \end{cases} f(x)={xα(exp(x)−1)if x>0if x≤0
   

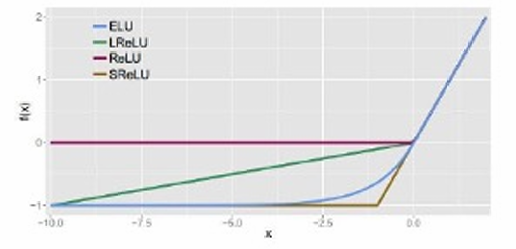
   在 x > 0 x>0 x>0时输出为 x x x，在 x < = 0 x<=0 x<=0时输出为 α ( e x p ( x ) − 1 ) α(exp(x)−1) α(exp(x)−1)。

   类似于Leaky ReLU，但使用指数函数来处理负值，有助于解决梯度消失问题，并且可以提供更好的性能。

1.2 神经网络的架构

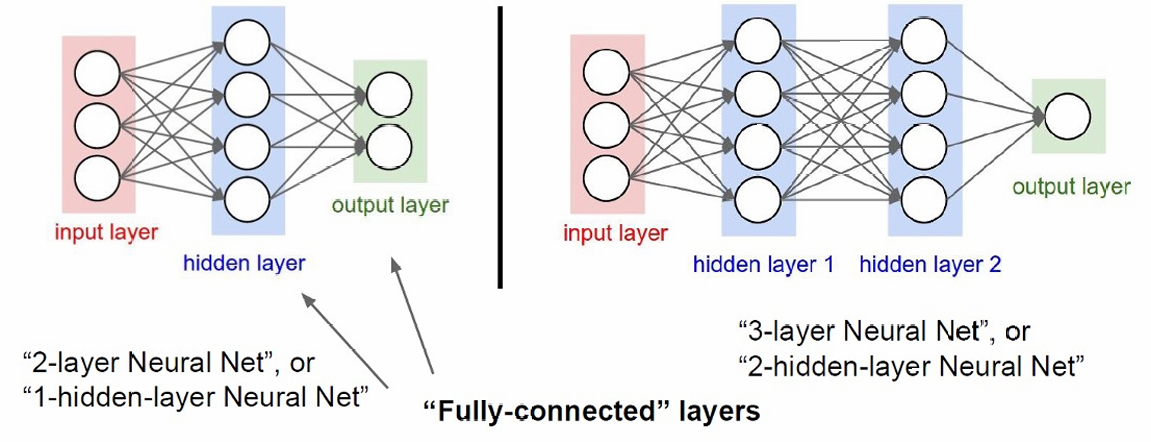
主要由三个部分组成：

输入层（input layer）：接收输入数据。

隐藏层（hidden layer）：处理输入数据，并通过激活函数引入非线性。

输出层（output layer）：产生最终的输出结果。

这里左边是单一隐藏层，右边是两层隐藏层。

每一层的每个神经元都与下一层的所有神经元相连，这种连接方式是全连接的。

1.3 神经网络的过程

前向传播是指数据从输入层经过隐藏层最终到达输出层的过程，其中每一层的输出成为下一层的输入。

这里给出代码示例。

f = lambda x: 1.0/(1.0 + np.exp(-x))
x = np.random.randn(3, 1)
h1 = f(np.dot(W1, x) + b1)
h2 = f(np.dot(W2, h1) + b2)
out = np.dot(W3, h2) + b3

这里定义了一个匿名函数f，使用Sigmoid函数作为激活函数。

然后生成一个包含3个随机数的列向量，作为输入层的输入。

再使用使用权重矩阵W1和偏置向量b1计算第一隐藏层的激活值。这里np.dot(W1, x)计算输入和权重的点积，然后加上偏置，最后通过激活函数f处理。

接着使用权重矩阵W2和偏置向量b2计算第二隐藏层的激活值，其中h1是第一隐藏层的输出。

最后使用权重矩阵W3和偏置向量b3计算输出层的激活值，其中h2是第二隐藏层的输出。这里没有应用激活函数，假设输出层直接输出线性组合的结果。

前向传播的下一步是损失计算。

线性模型的输出： s = f ( x ; W ) = W x s = f(x; W) = Wx s=f(x;W)=Wx

支持向量机（SVM）的损失函数： L i = ∑ j ≠ y i max ⁡ ( 0 , s j − s y i + 1 ) L_i = \sum_{j \neq y_i} \max(0, s_j - s_{y_i} + 1) Li=∑j=yimax(0,sj−syi+1)这个公式表示对于每个样本，计算其分数与其他所有样本分数的差异，如果这个差异大于1，则计算损失。

总损失函数： L = 1 N ∑ i = 1 N L i + ∑ k W k 2 L = \frac{1}{N} \sum_{i=1}^{N} L_i + \sum_k W_k^2 L=N1∑i=1NLi+∑kWk2，由两部分组成：

第一部分是数据损失，即所有样本损失的平均值。

第二部分是正则化项，用于防止过拟合。这里使用的是L2正则化，即权重的平方和。

计算完损失函数进入下一步后向传播（Backpropagation），

这里使用梯度下降来优化损失函数，这么做的目标是计算这个梯度 ∇ W L \nabla_W L ∇WL，以便更新权重，从而最小化损失函数。

利用链式法则从输出层向输入层反向计算梯度。

这一步的目的是确定如何调整网络参数以减少损失。

因此前向传播的计算过程如下图所示。

先通过输入和权重计算分数，然后算出单个样本的SVM损失，然后和正则化项一起得到总损失。

卷积神经网络（AlexNet架构）的过程如下图所示。

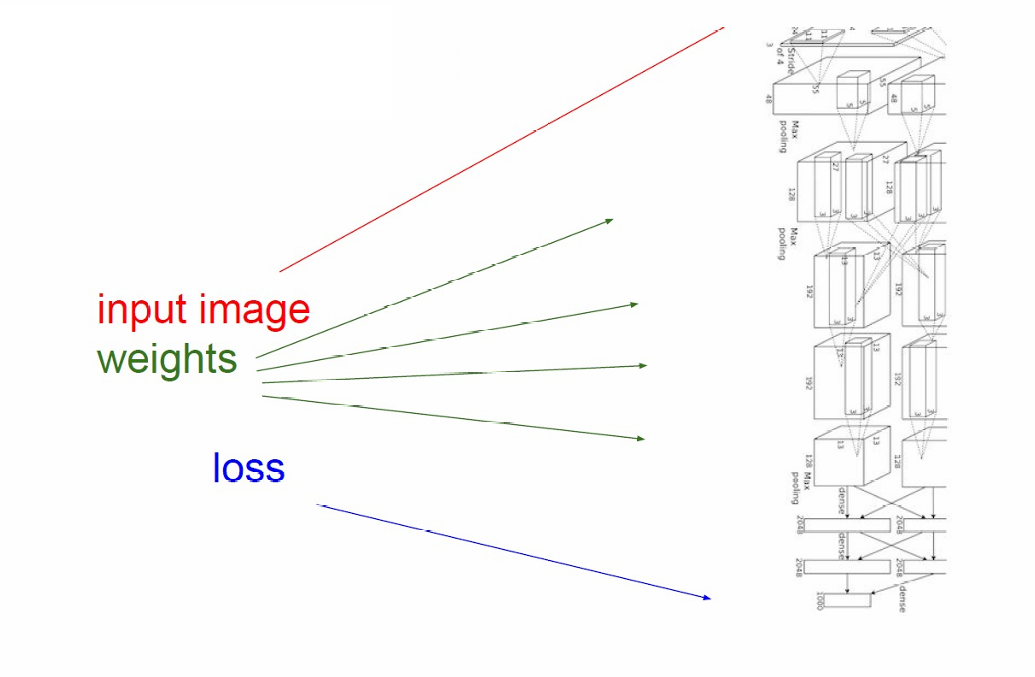
神经图灵机（Neural Turing Machine，NTM）的过程如下图所示。

我们来看一个例子。

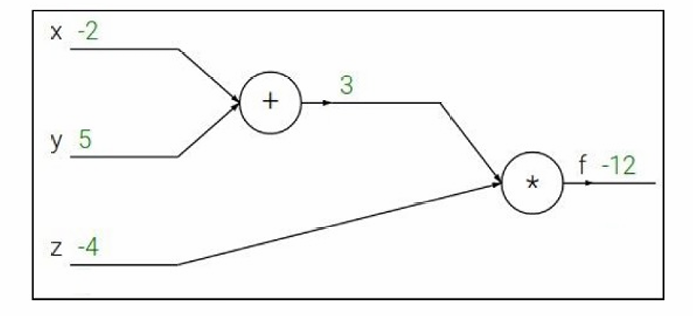
定义函数： f ( x , y , z ) = ( x + y ) z f(x,y,z)=(x+y)z f(x,y,z)=(x+y)z
q = x + y q=x+y q=x+y
f = q z f=qz f=qz

输入： x = − 2 x=-2 x=−2
y = 5 y=5 y=5
z = − 4 z=-4 z=−4

所以计算可以得到： q = 3 q=3 q=3
f = − 12 f=-12 f=−12

计算完后完成前向传播，我们现在计算暂时跳过计算损失函数，我们这个例子默认里面存在损失，现在我们利用反向传播更新网络参数以减少损失。

所以我们需要计算损失函数相对于输入变量 x x x, y y y, 和 z z z的梯度。在梯度下降优化算法中，需要计算损失函数相对于模型参数（包括输入变量）的梯度，以确定如何调整这些参数来减少损失。

对于 q = x + y q=x+y q=x+y，
∂ q ∂ x = 1 \frac{\partial q}{\partial x} = 1 ∂x∂q=1
∂ q ∂ y = 1 \frac{\partial q}{\partial y} = 1 ∂y∂q=1

对于 f = q z f=qz f=qz，
∂ f ∂ q = z \frac{\partial f}{\partial q} = z ∂q∂f=z
∂ f ∂ z = q \frac{\partial f}{\partial z} = q ∂z∂f=q

计算 ∂ f ∂ y \frac{\partial f}{\partial y} ∂y∂f使用链式法则，可以得到 ∂ f ∂ y = ∂ f ∂ q ∂ q ∂ y = z \frac{\partial f}{\partial y} = \frac{\partial f}{\partial q}\frac{\partial q}{\partial y}=z ∂y∂f=∂q∂f∂y∂q=z

计算 ∂ f ∂ x \frac{\partial f}{\partial x} ∂x∂f使用链式法则，可以得到 ∂ f ∂ y = ∂ f ∂ q ∂ q ∂ z = z \frac{\partial f}{\partial y} = \frac{\partial f}{\partial q}\frac{\partial q}{\partial z}=z ∂y∂f=∂q∂f∂z∂q=z

因此最后的结果如下图所示。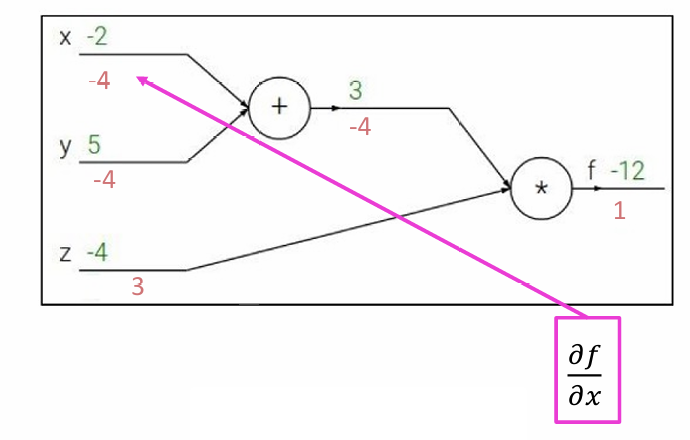

然后我们可以根据这里计算得到的梯度来更新网络中的权重。

1.3.1 链式法则（Chain Rule）

链式法则是微积分中用于计算复合函数导数的一个基本法则，我们来回顾一下。

使用链式法则可以通过将损失函数相对于中间变量 z z z的梯度与中间变量 z z z相对于输入 x x x和 y y y的梯度相乘，来计算损失函数相对于输入 x x x和 y y y的梯度。
∂ L ∂ x = ∂ L ∂ z ∂ z ∂ x \frac{\partial L}{\partial x} = \frac{\partial L}{\partial z}\frac{\partial z}{\partial x} ∂x∂L=∂z∂L∂x∂z
∂ L ∂ y = ∂ L ∂ z ∂ z ∂ y \frac{\partial L}{\partial y} = \frac{\partial L}{\partial z}\frac{\partial z}{\partial y} ∂y∂L=∂z∂L∂y∂z

下面我们尝试一个比较复杂的例子。

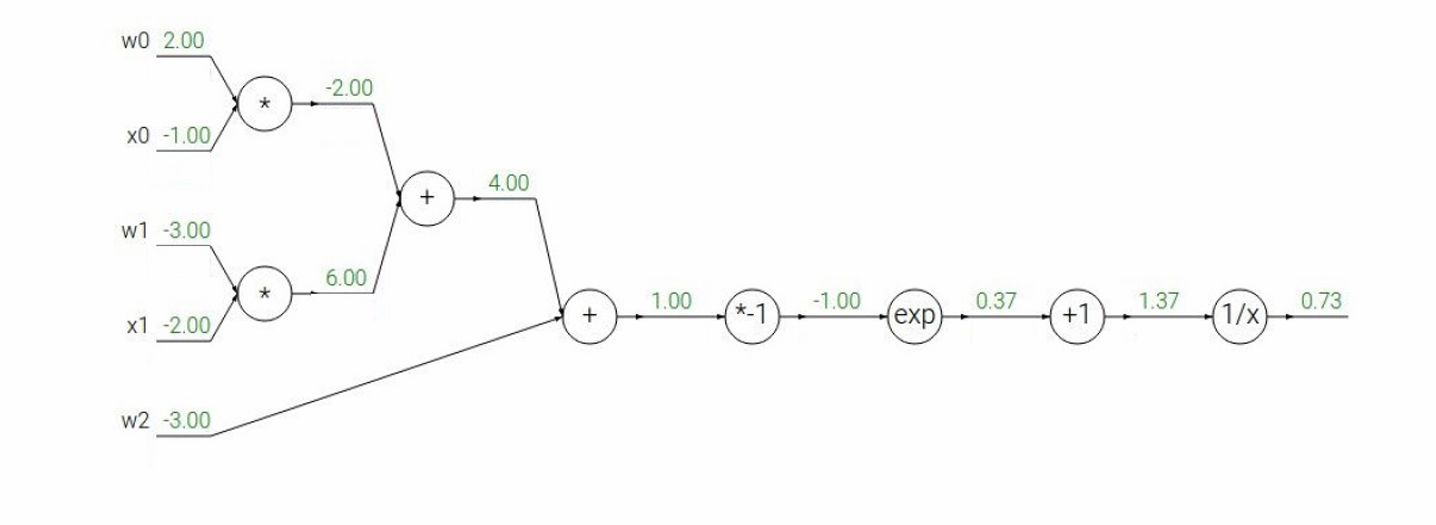
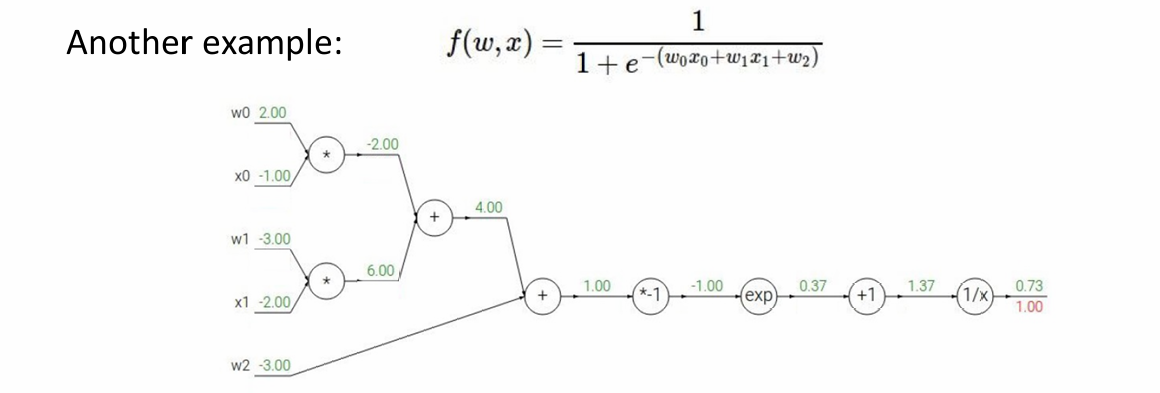
函数： f ( w , x ) = 1 1 + e − ( w 0 x 0 + w 1 x 1 + w 2 ) f(w, x) = \frac{1}{1 + e^{-(w_0x_0 + w_1x_1 + w_2)}} f(w,x)=1+e−(w0x0+w1x1+w2)1

我们先接受输入计算 z = w 0 x 0 + w 1 x 1 + w 2 z=w_0x_0+w_1x_1+w_2 z=w0x0+w1x1+w2
z = 2.00 × ( − 1.00 ) + ( − 3.00 ) × ( − 2.00 ) + ( − 3.00 ) = − 2.00 + 6.00 − 3.00 = 1.00 z=2.00×(−1.00)+(−3.00)×(−2.00)+(−3.00)=−2.00+6.00−3.00=1.00 z=2.00×(−1.00)+(−3.00)×(−2.00)+(−3.00)=−2.00+6.00−3.00=1.00

因此 − z = − 1 -z=-1 −z=−1
e x p ( − z ) = e x p ( − 1.00 ) ≈ 0.37 exp(−z)=exp(−1.00)≈0.37 exp(−z)=exp(−1.00)≈0.37

计算 e x p ( − z ) + 1 exp(−z)+1 exp(−z)+1： e x p ( − 1.00 ) + 1 ≈ 0.37 + 1 = 1.37 exp(−1.00)+1≈0.37+1=1.37 exp(−1.00)+1≈0.37+1=1.37

最后，计算 1 x \frac{1}{x} x1： 1 1.37 ≈ 0.73 \frac{1}{1.37}≈0.73 1.371≈0.73

先看一下基础函数的导数： f ( x ) = e x ⇒ d f d x = e x f(x) = e^x \Rightarrow \quad \frac{df}{dx} = e^x f(x)=ex⇒dxdf=ex
f a ( x ) = a x ⇒ d f d x = a f_a(x) = ax \Rightarrow \quad \frac{df}{dx} = a fa(x)=ax⇒dxdf=a
f ( x ) = 1 x ⇒ d f d x = − 1 x 2 f(x) = \frac{1}{x} \Rightarrow \quad \frac{df}{dx} = -\frac{1}{x^2} f(x)=x1⇒dxdf=−x21
f c ( x ) = c + x ⇒ d f d x = 1 f_c(x) = c + x \Rightarrow \quad \frac{df}{dx} = 1 fc(x)=c+x⇒dxdf=1

然后我们开始反向传播，首先是起点， f f f对 f f f的梯度，即： ∂ f ∂ f = 1.00 \frac{∂f}{∂f}=1.00 ∂f∂f=1.00

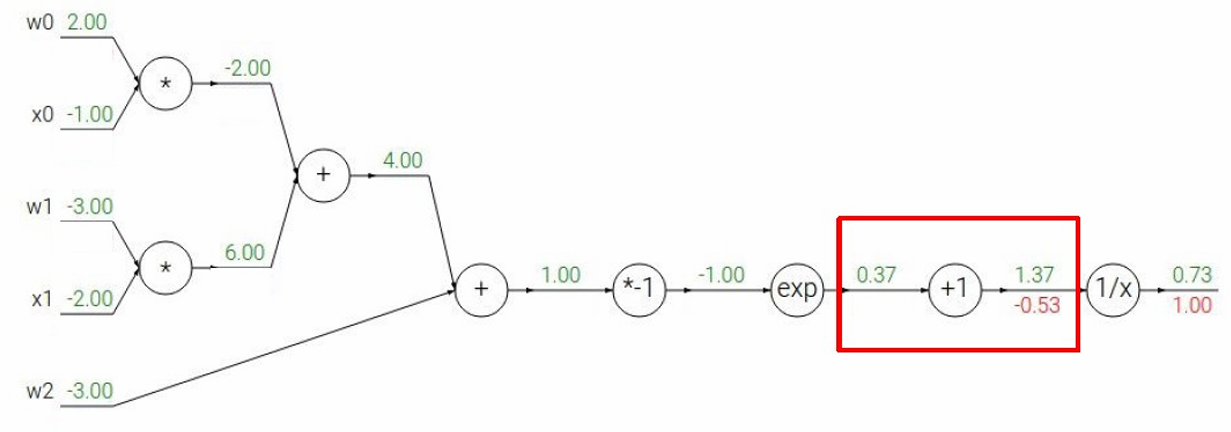
然后下一步，经过 f = 1 a f=\frac{1}{a} f=a1节点，我们要计算 ∂ L ∂ a \frac{∂L}{∂a} ∂a∂L

根据链式法则 ∂ L ∂ a = ∂ f ∂ a ∂ L ∂ f \frac{∂L}{∂a}=\frac{∂f}{∂a}\frac{∂L}{∂f} ∂a∂L=∂a∂f∂f∂L

因为 ∂ f ∂ a = − 1 a 2 \frac{∂f}{∂a}=-\frac{1}{a^2} ∂a∂f=−a21

所以 ∂ L ∂ a = − 1 a 2 ∂ L ∂ f = − 1 1.3 7 2 ( 1.00 ) = − 0.53 \frac{∂L}{∂a}=-\frac{1}{a^2}\frac{∂L}{∂f}=-\frac{1}{1.37^2}(1.00)=-0.53 ∂a∂L=−a21∂f∂L=−1.3721(1.00)=−0.53

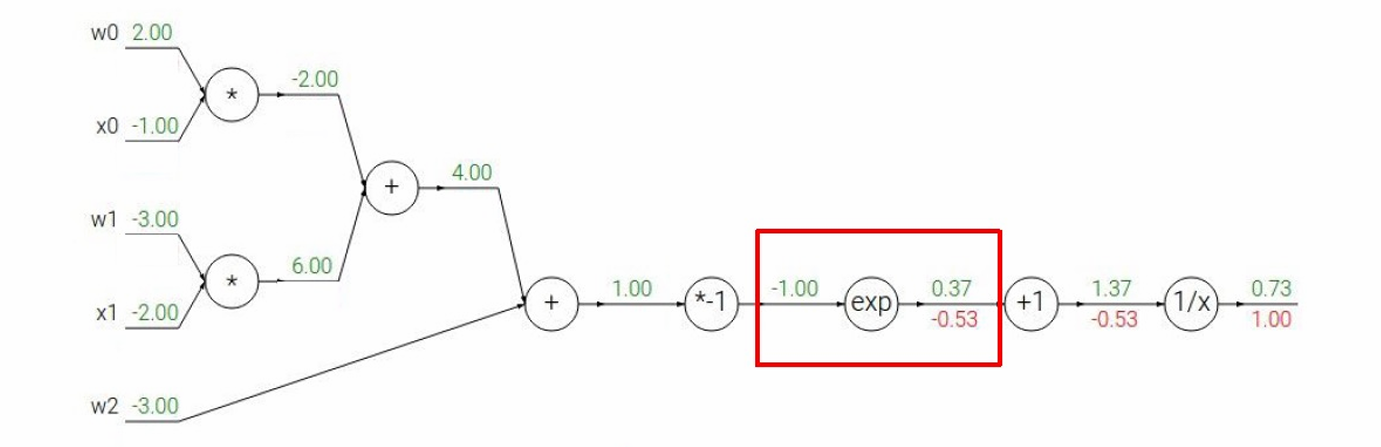
然后下一步，经过 a = 1 + t a=1+t a=1+t节点，我们要计算 ∂ L ∂ t \frac{∂L}{∂t} ∂t∂L

根据链式法则 ∂ L ∂ a = ∂ a ∂ t ∂ L ∂ a \frac{∂L}{∂a}=\frac{∂a}{∂t}\frac{∂L}{∂a} ∂a∂L=∂t∂a∂a∂L

因为 ∂ a ∂ t = 1 \frac{∂a}{∂t}=1 ∂t∂a=1（因为 a = 1 + t a = 1 + t a=1+t 对 t t t 的导数为 1）

所以 ∂ L ∂ t = 1 × ( − 0.53 ) = − 0.53 \frac{∂L}{∂t}=1×(−0.53)=−0.53 ∂t∂L=1×(−0.53)=−0.53

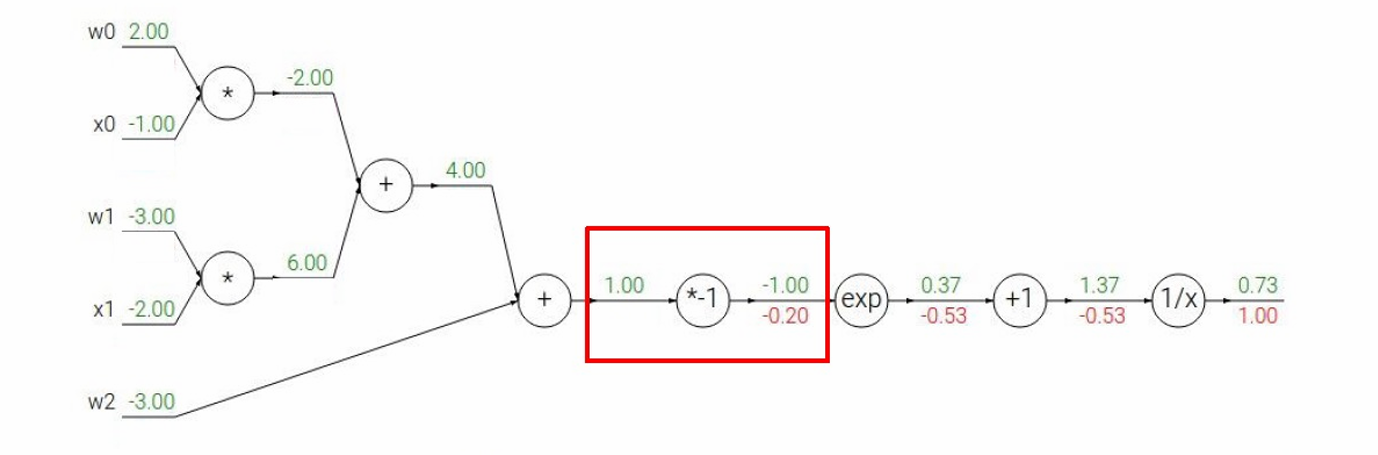
然后下一步，经过 t = e u t=e^u t=eu节点，我们要计算 ∂ L ∂ u \frac{∂L}{∂u} ∂u∂L

根据链式法则 ∂ L ∂ u = ∂ t ∂ u ∂ L ∂ t \frac{∂L}{∂u}=\frac{∂t}{∂u}\frac{∂L}{∂t} ∂u∂L=∂u∂t∂t∂L

因为 ∂ t ∂ u = e u \frac{∂t}{∂u}=e^u ∂u∂t=eu

所以 ∂ L ∂ u = e u × ∂ L ∂ t = ≈ 0.37 × ( − 0.53 ) ≈ − 0.196 \frac{∂L}{∂u}=e^u×\frac{∂L}{∂t}=≈0.37×(−0.53)≈−0.196 ∂u∂L=eu×∂t∂L=≈0.37×(−0.53)≈−0.196

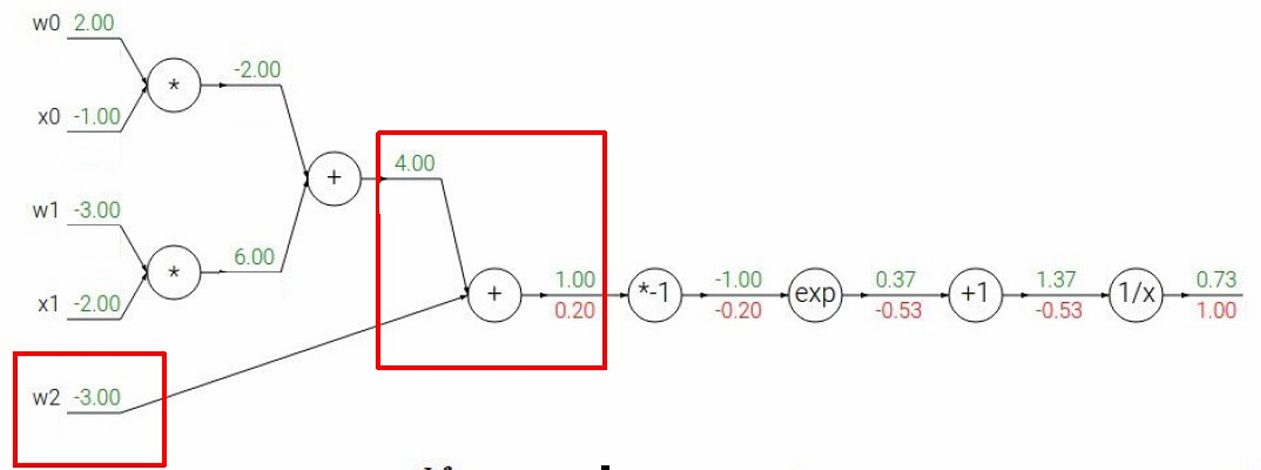
然后下一步，经过 u = − z u=−z u=−z节点，我们要计算 ∂ L ∂ z \frac{∂L}{∂z} ∂z∂L

根据链式法则 ∂ L ∂ z = ∂ u ∂ z ∂ L ∂ u \frac{∂L}{∂z}=\frac{∂u}{∂z}\frac{∂L}{∂u} ∂z∂L=∂z∂u∂u∂L

因为 u = − z u=-z u=−z

所以 ∂ L ∂ z = ( − 1 ) × ( − 0.20 ) = 0.20 \frac{∂L}{∂z}=(−1)×(−0.20)=0.20 ∂z∂L=(−1)×(−0.20)=0.20

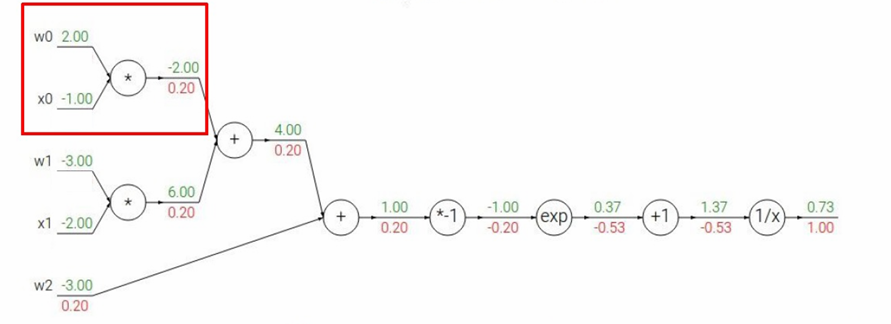
然后下一步，经过 z = A + B + C z=A+B+C z=A+B+C节点，其中： A = w 0 x 0 A=w_0x_0 A=w0x0
B = w 1 x 1 B=w_1x_1 B=w1x1
C = w 2 C=w_2 C=w2

我们要计算 ∂ L ∂ A \frac{∂L}{∂A} ∂A∂L， ∂ L ∂ B \frac{∂L}{∂B} ∂B∂L， ∂ L ∂ C \frac{∂L}{∂C} ∂C∂L

根据链式法则 ∂ L ∂ A = ∂ z ∂ A ∂ L ∂ z = 1 × 0.20 = 0.20 \frac{∂L}{∂A}=\frac{∂z}{∂A}\frac{∂L}{∂z}=1×0.20=0.20 ∂A∂L=∂A∂z∂z∂L=1×0.20=0.20
∂ L ∂ B = ∂ z ∂ B ∂ L ∂ z = 1 × 0.20 = 0.20 \frac{∂L}{∂B}=\frac{∂z}{∂B}\frac{∂L}{∂z}=1×0.20=0.20 ∂B∂L=∂B∂z∂z∂L=1×0.20=0.20
∂ L ∂ C = ∂ z ∂ C ∂ L ∂ z = 1 × 0.20 = 0.20 \frac{∂L}{∂C}=\frac{∂z}{∂C}\frac{∂L}{∂z}=1×0.20=0.20 ∂C∂L=∂C∂z∂z∂L=1×0.20=0.20

也就是局部梯度（local gradient）乘以上游梯度（its gradient，从后面传回来的梯度）

然后下一步，经过 w 0 × x 0 w_0×x_0 w0×x0节点，其中： A = w 0 x 0 A=w_0x_0 A=w0x0
w 0 = 2.00 w_0=2.00 w0=2.00
x 0 = − 1.00 x_0=-1.00 x0=−1.00

我们要计算 ∂ L ∂ w 0 \frac{∂L}{∂w_0} ∂w0∂L， ∂ L ∂ x 0 \frac{∂L}{∂x_0} ∂x0∂L

根据链式法则 ∂ L ∂ w 0 = ∂ A ∂ w 0 ∂ L ∂ A = x 0 × 0.20 = ( − 1.00 ) × 0.20 = − 0.20 \frac{∂L}{∂w_0}=\frac{∂A}{∂w_0}\frac{∂L}{∂A}=x_0×0.20=(−1.00)×0.20=−0.20 ∂w0∂L=∂w0∂A∂A∂L=x0×0.20=(−1.00)×0.20=−0.20
∂ L ∂ x 0 = ∂ A ∂ x 0 ∂ L ∂ A = w 0 × 0.20 = 2.00 × 0.20 = 0.40 \frac{∂L}{∂x_0}=\frac{∂A}{∂x_0}\frac{∂L}{∂A}=w_0×0.20=2.00×0.20=0.40 ∂x0∂L=∂x0∂A∂A∂L=w0×0.20=2.00×0.20=0.40

类似地，我们可以计算得到另一边 w 1 × x 1 w_1×x_1 w1×x1节点的结果是 ∂ L ∂ w 1 = ∂ B ∂ w 1 ∂ L ∂ B = x 1 × 0.20 = ( − 2.00 ) × 0.20 = − 0.40 \frac{∂L}{∂w_1}=\frac{∂B}{∂w_1}\frac{∂L}{∂B}=x_1×0.20=(−2.00)×0.20=−0.40 ∂w1∂L=∂w1∂B∂B∂L=x1×0.20=(−2.00)×0.20=−0.40
∂ L ∂ x 1 = ∂ B ∂ x 1 ∂ L ∂ B = w 1 × 0.20 = − 3.00 × 0.20 = 0.60 \frac{∂L}{∂x_1}=\frac{∂B}{∂x_1}\frac{∂L}{∂B}=w_1×0.20=-3.00×0.20=0.60 ∂x1∂L=∂x1∂B∂B∂L=w1×0.20=−3.00×0.20=0.60

当然我们这里是一步一步通过链式法则解决的，我们也可以将其看作一个完整的函数也就是将整个 Sigmoid 函数看作一个计算节点（gate）。

Sigmoid 函数： σ ( x ) = 1 1 + e − x \sigma(x) = \frac{1}{1 + e^{-x}} σ(x)=1+e−x1

Sigmoid 的导数为： d σ ( x ) d x = σ ( x ) ( 1 − σ ( x ) ) \frac{d\sigma(x)}{dx} = \sigma(x)(1 - \sigma(x)) dxdσ(x)=σ(x)(1−σ(x))

推导过程： σ ′ ( x ) = e − x ( 1 + e − x ) 2 = 1 + e − x − 1 1 + e − x = σ ( x ) ( 1 − σ ( x ) ) \sigma'(x) =\frac{e^{-x}}{{(1+e^{-x})}^2}=\frac{1+e^{-x}-1}{{1+e^{-x}}}= \sigma(x)(1 - \sigma(x)) σ′(x)=(1+e−x)2e−x=1+e−x1+e−x−1=σ(x)(1−σ(x))

计算结果： ( 0.73 ) ∗ ( 1 − 0.73 ) = 0.2 (0.73)*(1-0.73)=0.2 (0.73)∗(1−0.73)=0.2

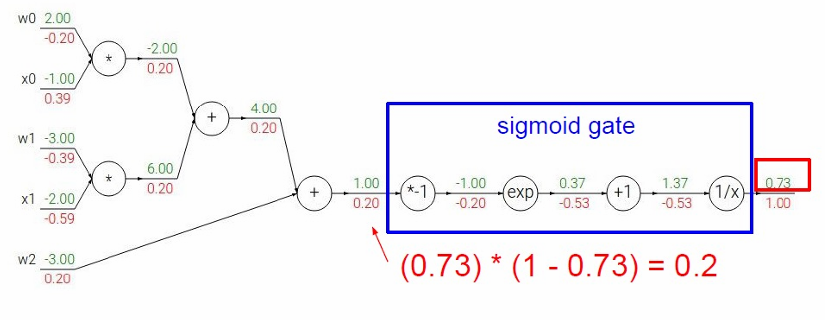
这与我们之前反向传播得到的结果一致。

1.3.1.1 三种基本节点的反向传播模式

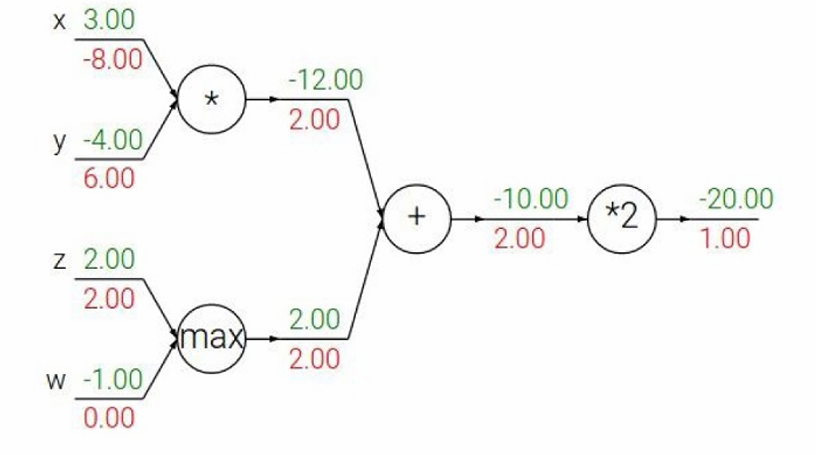
有三种基本节点：

1. 加法节点（add gate）：梯度分配器（gradient distributor）
   特点：将上游梯度原样分配给所有输入
   原理： z = x + y z=x+y z=x+y， ∂ z ∂ x = 1 \frac{∂z}{∂x}=1 ∂x∂z=1 ， ∂ z ∂ y = 1 \frac{∂z}{∂y}=1 ∂y∂z=1
   例子：上游梯度为 2.00，两个输入都得到 2.00
2. 乘法节点（mul gate）：梯度交换器（gradient switcher）
   特点：将上游梯度乘以另一个输入的值后传递
   原理： z = x × y z=x×y z=x×y， ∂ z ∂ x = y \frac{∂z}{∂x}=y ∂x∂z=y ， ∂ z ∂ y = x \frac{∂z}{∂y}=x ∂y∂z=x
   例子： ∂ L ∂ x = y × 2.00 = − 4.00 × 2.00 = − 8.00 \frac{∂L}{∂x}=y×2.00=−4.00×2.00=−8.00 ∂x∂L=y×2.00=−4.00×2.00=−8.00
   ∂ L ∂ y = x × 2.00 = 3.00 × 2.00 = 6.00 \frac{∂L}{∂y}=x×2.00=3.00×2.00=6.00 ∂y∂L=x×2.00=3.00×2.00=6.00
3. 最大值节点（max gate）：梯度路由器（gradient router）
   特点：只将梯度传递给较大的输入，较小输入得到零梯度
   原理： z = m a x ( x , y ) z=max(x,y) z=max(x,y)
   如果 x > y x>y x>y，则 ∂ z ∂ x = 1 \frac{∂z}{∂x}=1 ∂x∂z=1， ∂ z ∂ y = 0 \frac{∂z}{∂y}=0 ∂y∂z=0
   如果 y > x y>x y>x，则 ∂ z ∂ x = 0 \frac{∂z}{∂x}=0 ∂x∂z=0， ∂ z ∂ y = 1 \frac{∂z}{∂y}=1 ∂y∂z=1
   例子中，因为 x x x较大所以 ∂ L ∂ x = 2.00 \frac{∂L}{∂x}=2.00 ∂x∂L=2.00， ∂ L ∂ y = 0.00 \frac{∂L}{∂y}=0.00 ∂y∂L=0.00

1.3.1.2 池化的反向传播

1. Lp池化（Lp-pooling）
   y = ( ∑ i x i p ) 1 p y = \left( \sum_i x_i^p \right)^{\frac{1}{p}} y=(∑ixip)p1，其中 x i > 0 x_i > 0 xi>0。
   已知： y ′ = ∂ L ∂ y y' = \frac{\partial L}{\partial y} y′=∂y∂L
   求： x i ′ = ∂ L ∂ x i x_i' = \frac{\partial L}{\partial x_i} xi′=∂xi∂L
   我们设 S = ∑ i x i p S = \sum_i x_i^p S=∑ixip，则$ y = S 1 / p y = S^{1/p} y=S1/p
   先求 ∂ y ∂ x i \frac{\partial y}{\partial x_i} ∂xi∂y：
   ∂ y ∂ x i = 1 p S 1 p − 1 ⋅ p x i p − 1 = S 1 p − 1 x i p − 1 \frac{\partial y}{\partial x_i} = \frac{1}{p} S^{\frac{1}{p} - 1} \cdot p x_i^{p-1} = S^{\frac{1}{p} - 1} x_i^{p-1} ∂xi∂y=p1Sp1−1⋅pxip−1=Sp1−1xip−1
   由于 y = S 1 / p y = S^{1/p} y=S1/p，所以 S 1 p − 1 = y S = y ∑ j x j p S^{\frac{1}{p} - 1} = \frac{y}{S} = \frac{y}{\sum_j x_j^p} Sp1−1=Sy=∑jxjpy。
   因此： ∂ y ∂ x i = y ∑ j x j p x i p − 1 \frac{\partial y}{\partial x_i} = \frac{y}{\sum_j x_j^p} x_i^{p-1} ∂xi∂y=∑jxjpyxip−1
   最终： x i ′ = ∂ L ∂ x i = ∂ L ∂ y ⋅ ∂ y ∂ x i = y ′ ⋅ y ∑ j x j p x i p − 1 x_i' = \frac{\partial L}{\partial x_i} = \frac{\partial L}{\partial y} \cdot \frac{\partial y}{\partial x_i} = y' \cdot \frac{y}{\sum_j x_j^p} x_i^{p-1} xi′=∂xi∂L=∂y∂L⋅∂xi∂y=y′⋅∑jxjpyxip−1
2. 对数平均池化（log-average module）
   y = 1 β ln ⁡ ( 1 n ∑ i exp ⁡ ( β x i ) ) y = \frac{1}{\beta} \ln \left( \frac{1}{n} \sum_i \exp(\beta x_i) \right) y=β1ln(n1∑iexp(βxi))
   已知： y ′ = ∂ L ∂ y y' = \frac{\partial L}{\partial y} y′=∂y∂L
   求： x i ′ = ∂ L ∂ x i x_i' = \frac{\partial L}{\partial x_i} xi′=∂xi∂L
   我们设 S = 1 n ∑ i exp ⁡ ( β x i ) S = \frac{1}{n} \sum_i \exp(\beta x_i) S=n1∑iexp(βxi)，则 y = 1 β ln ⁡ S y = \frac{1}{\beta} \ln S y=β1lnS。
   先求 ∂ y ∂ x i \frac{\partial y}{\partial x_i} ∂xi∂y：
   ∂ y ∂ x i = 1 β ⋅ 1 S ⋅ ∂ S ∂ x i = 1 β ⋅ 1 S ⋅ 1 n ⋅ β exp ⁡ ( β x i ) \frac{\partial y}{\partial x_i} = \frac{1}{\beta} \cdot \frac{1}{S} \cdot \frac{\partial S}{\partial x_i} = \frac{1}{\beta} \cdot \frac{1}{S} \cdot \frac{1}{n} \cdot \beta \exp(\beta x_i) ∂xi∂y=β1⋅S1⋅∂xi∂S=β1⋅S1⋅n1⋅βexp(βxi)
   ∂ y ∂ x i = exp ⁡ ( β x i ) n S \frac{\partial y}{\partial x_i} = \frac{\exp(\beta x_i)}{nS} ∂xi∂y=nSexp(βxi)
   由于 S = 1 n ∑ j exp ⁡ ( β x j ) S = \frac{1}{n} \sum_j \exp(\beta x_j) S=n1∑jexp(βxj)，且 β y = ln ⁡ S \beta y = \ln S βy=lnS，所以 S = exp ⁡ ( β y ) S = \exp(\beta y) S=exp(βy)。
   因此： ∂ y ∂ x i = exp ⁡ ( β x i ) n exp ⁡ ( β y ) = exp ⁡ ( β x i − β y ) n \frac{\partial y}{\partial x_i} = \frac{\exp(\beta x_i)}{n \exp(\beta y)} = \frac{\exp(\beta x_i - \beta y)}{n} ∂xi∂y=nexp(βy)exp(βxi)=nexp(βxi−βy)
   最终： x i ′ = ∂ L ∂ x i = ∂ L ∂ y ⋅ ∂ y ∂ x i = y ′ ⋅ exp ⁡ ( β ( x i − y ) ) n x_i' = \frac{\partial L}{\partial x_i} = \frac{\partial L}{\partial y} \cdot \frac{\partial y}{\partial x_i} = y' \cdot \frac{\exp(\beta (x_i - y))}{n} xi′=∂xi∂L=∂y∂L⋅∂xi∂y=y′⋅nexp(β(xi−y))

1.3.1.3 向量时的梯度计算

在之前的例子中， x , y , z x,y,z x,y,z都是标量（单个数值）。现在考虑它们都是向量的情况。

我们用雅可比矩阵来描述向量值函数变化率，其中每个元素是 z z z的一个分量对 x x x的一个分量的偏导数。

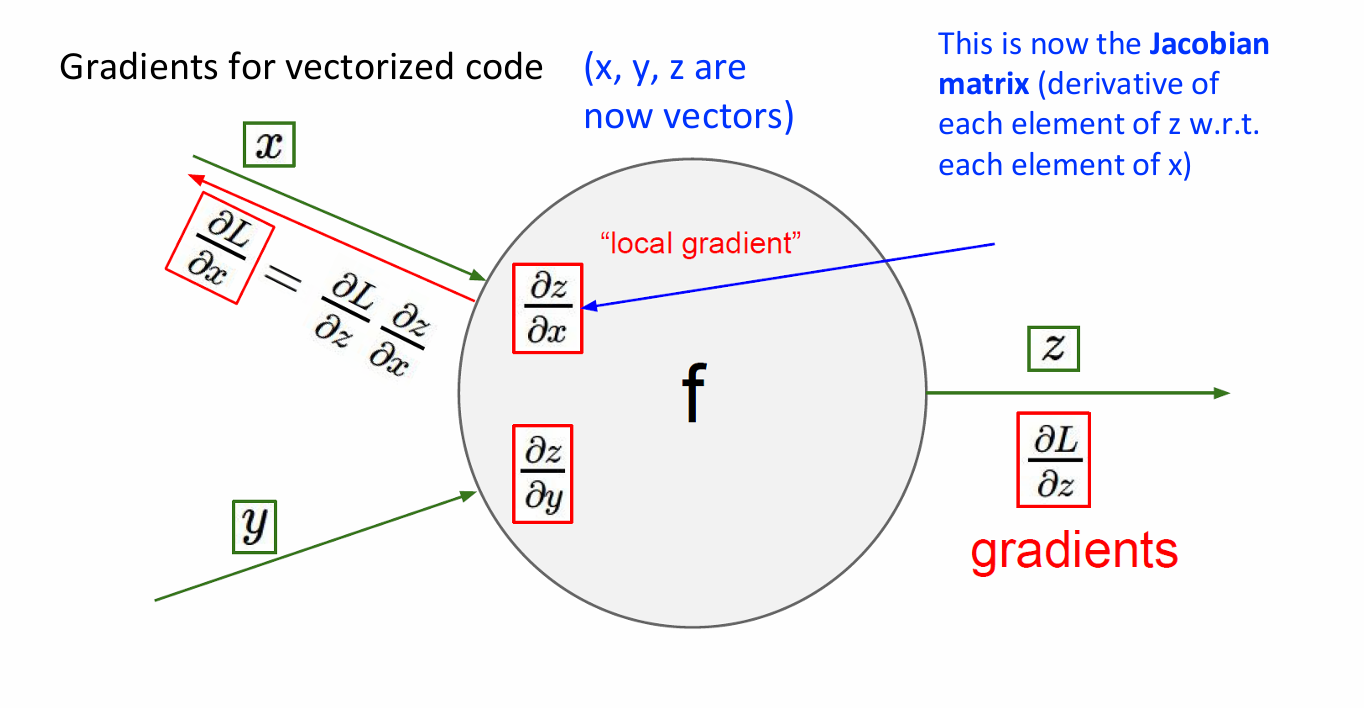
向量化操作如下。

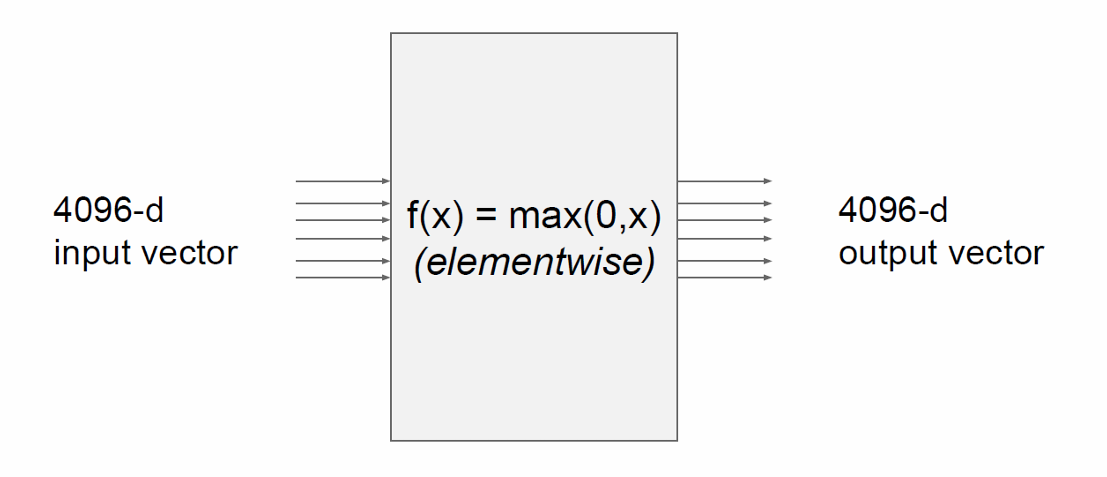
由于输入和输出都是4096维向量，且每个输出元素都是输入元素的逐元素操作的结果，因此雅可比矩阵是一个4096x4096的矩阵。这是因为每个输出元素对每个输入元素都有一个偏导数，形成了一个完整的矩阵。

我们这里使用的函数是ReLU函数，此时雅可比矩阵是一个稀疏矩阵，其中大部分元素为0，只有当输入元素 x i > 0 x_i>0 xi>0时，对应的偏导数为1。因此，雅可比矩阵中只有少数元素为1，其余为0。

理论上，如果考虑整个minibatch，雅可比矩阵的大小将是 409600×409600。这是因为每个输入向量有4096个元素，minibatch中有100个这样的向量，所以总的输入维度是 4096×100=409600，输出也是如此。

在实际应用中，尽管理论上雅可比矩阵的大小是 409600×409600，但在实践中，由于ReLU函数的特性（其导数在正值区域为1，在非正值区域为0），雅可比矩阵通常是稀疏的。这意味着在计算梯度时，我们只需要关注那些输入值为正的元素，从而大大减少了计算量，提升了计算效率。

我们现在看一个例子，用向量化操作计算L2范数（也称为欧几里得范数）的平方

f ( x , W ) = ∥ W ⋅ x ∥ 2 = ∑ i = 1 n ( W ⋅ x ) i 2 f(x, W) = \|W \cdot x\|^2 = \sum_{i=1}^{n} (W \cdot x)_i^2 f(x,W)=∥W⋅x∥2=∑i=1n(W⋅x)i2，其中 x x x是一个 R n R^n Rn维的向量， W W W是一个 R n × n R^{n×n} Rn×n维的矩阵。

我们给定输入值矩阵，如下图示。

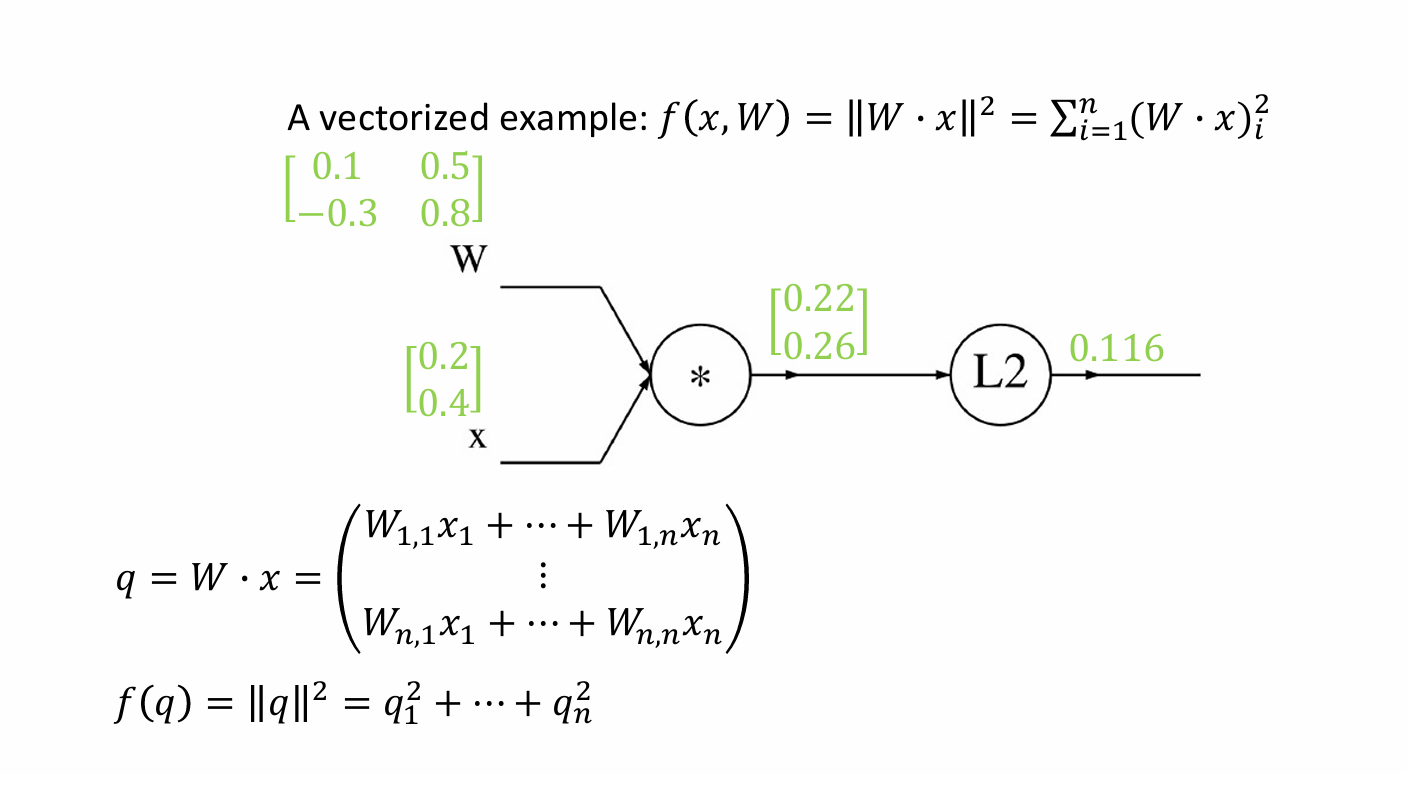
我们先进行前向计算：
q = W x = [ 0.1 × 0.2 + 0.5 × 0.4 − 0.3 × 0.2 + 0.8 × 0.4 ] = [ 0.22 0.26 ] , f = ∥ q ∥ 2 = 0.2 2 2 + 0.2 6 2 = 0.116 q = W x =\begin{bmatrix} 0.1×0.2+0.5×0.4 \\ -0.3×0.2+0.8×0.4 \end{bmatrix} =\begin{bmatrix} 0.22 \\ 0.26 \end{bmatrix}, \quad f = \|q\|^2 =0.22^2+0.26^2=0.116 q=Wx=[0.1×0.2+0.5×0.4−0.3×0.2+0.8×0.4]=[0.220.26],f=∥q∥2=0.222+0.262=0.116

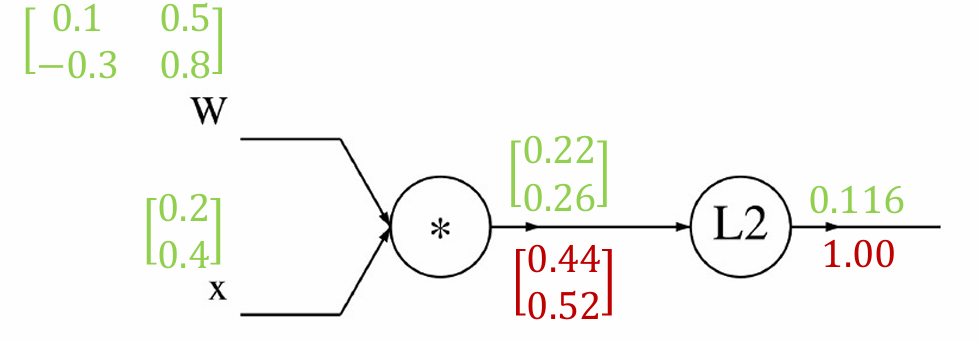
再计算反向传播梯度。

从损失 f f f开始， ∂ f ∂ f = 1.00 \frac{\partial f}{\partial f} = 1.00 ∂f∂f=1.00

计算梯度： ∂ f ∂ q i = ( q 1 2 + q 2 2 ) ∂ q i = 2 q i \frac{\partial f}{\partial q_i} = \frac{(q_1^2+q_2^2)}{\partial q_i}=2q_i ∂qi∂f=∂qi(q12+q22)=2qi
∇ q f = 2 q = [ 0.44 0.52 ] \quad \nabla_q f = 2q = \begin{bmatrix} 0.44 \\ 0.52 \end{bmatrix} ∇qf=2q=[0.440.52]

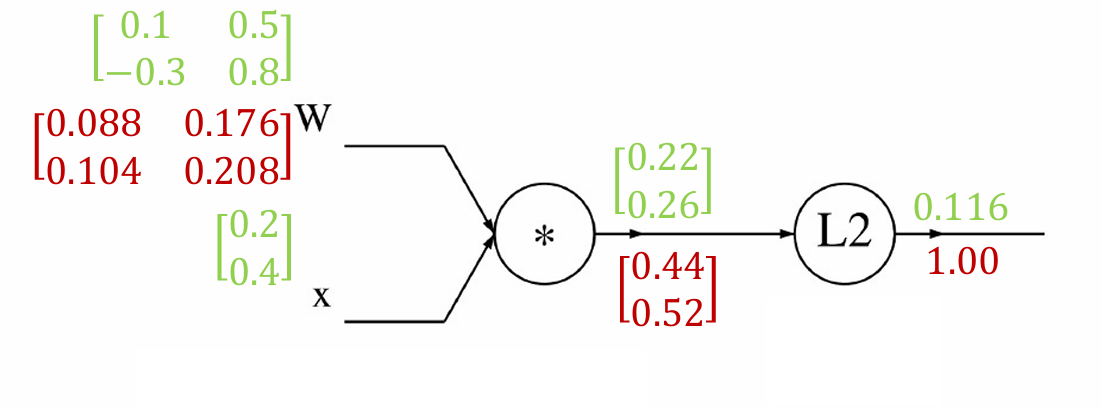
我们现在计算 f f f对权重矩阵 W W W的梯度。

使用链式法则： ∂ f ∂ W i , j = ∑ k ∂ f ∂ q k ∂ q k ∂ W i , j \frac{\partial f}{\partial W_{i,j}} = \sum_k \frac{\partial f}{\partial q_k} \frac{\partial q_k}{\partial W_{i,j}} ∂Wi,j∂f=∑k∂qk∂f∂Wi,j∂qk

其中： ∂ f ∂ q k = 2 q k \frac{\partial f}{\partial q_k} = 2q_k ∂qk∂f=2qk
∂ q k ∂ W i , j = 1 k = i x j \frac{\partial q_k}{\partial W_{i,j}} = 1_{k=i} x_j ∂Wi,j∂qk=1k=ixj( q k = ∑ l W k , l x l q_k = \sum_l W_{k,l} x_l qk=∑lWk,lxl， ∂ q k ∂ W i , j = { x j if k = i 0 otherwise \frac{\partial q_k}{\partial W_{i,j}} = \begin{cases} x_j & \text{if } k = i \\ 0 & \text{otherwise} \end{cases} ∂Wi,j∂qk={xj0if k=iotherwise)

代入得： ∂ f ∂ W i , j = ∑ k ( 2 q k ) ( 1 k = i x j ) = 2 q i x j \frac{\partial f}{\partial W_{i,j}} = \sum_k (2q_k)(1_{k=i} x_j) = 2q_i x_j ∂Wi,j∂f=∑k(2qk)(1k=ixj)=2qixj

矩阵形式： ∇ W f = 2 q x ⊤ \nabla_W f = 2q x^\top ∇Wf=2qx⊤

所以 ∇ W f = 2 × [ 0.22 0.26 ] [ 0.2 0.4 ] = [ 0.088 0.176 0.104 0.208 ] \nabla_W f = 2 \times \begin{bmatrix} 0.22 \\ 0.26 \end{bmatrix} \begin{bmatrix} 0.2 & 0.4 \end{bmatrix} = \begin{bmatrix} 0.088 & 0.176 \\ 0.104 & 0.208 \end{bmatrix} ∇Wf=2×[0.220.26][0.20.4]=[0.0880.1040.1760.208]

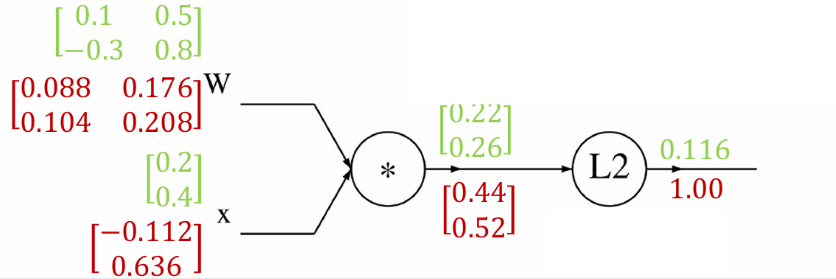
我们现在计算输入向量 x x x对权重矩阵 W W W的梯度。

使用链式法则： ∂ f ∂ x i = ∑ k ∂ f ∂ q k ∂ q k ∂ x i \frac{\partial f}{\partial x_{i}} = \sum_k \frac{\partial f}{\partial q_k} \frac{\partial q_k}{\partial x_{i}} ∂xi∂f=∑k∂qk∂f∂xi∂qk

其中： ∂ f ∂ q k = 2 q k \frac{\partial f}{\partial q_k} = 2q_k ∂qk∂f=2qk
∂ q k ∂ x i = W k , i \frac{\partial q_k}{\partial x_{i}} = W_{k,i} ∂xi∂qk=Wk,i( q k = ∑ l W k , l x l q_k = \sum_l W_{k,l} x_l qk=∑lWk,lxl)

代入得： ∂ f ∂ x i = ∑ k ( 2 q k ) W k , i \frac{\partial f}{\partial x_i} = \sum_k (2q_k) W_{k,i} ∂xi∂f=∑k(2qk)Wk,i

矩阵形式： ∇ x f = 2 W ⊤ q \nabla_x f = 2W^\top q ∇xf=2W⊤q

所以 ∇ x f = 2 × [ 0.1 − 0.3 0.5 0.8 ] [ 0.22 0.26 ] = [ − 0.112 0.636 ] \nabla_x f = 2 \times \begin{bmatrix} 0.1 & -0.3 \\ 0.5 & 0.8 \end{bmatrix} \begin{bmatrix} 0.22 \\ 0.26 \end{bmatrix} = \begin{bmatrix} -0.112 \\ 0.636 \end{bmatrix} ∇xf=2×[0.10.5−0.30.8][0.220.26]=[−0.1120.636]