自己动手写深度学习框架（神经网络的引入）

最早读神经网络的时候，就觉得这个单词有点夸大其词了。直觉上来说，这里的神经网络，更多的是区别于感知机本身。感知机多使用线性函数进行处理，而神经网络多采用阶跃、sigmoid或者是relu这样的函数来处理。只是后来因为处理图像，引入了cnn；又因为处理声音，引入了rnn。所以，如果从延续性来说，神经网络可以看成是感知机的一个衍生和拓展。

1、新的激励函数

前面说过，感知机主要是线性函数，即

y = k1 * x1 + k2 * x2 + ...

而神经网络则采用了非线性函数。比如阶跃函数，

y = (x > 0) ? 1:0

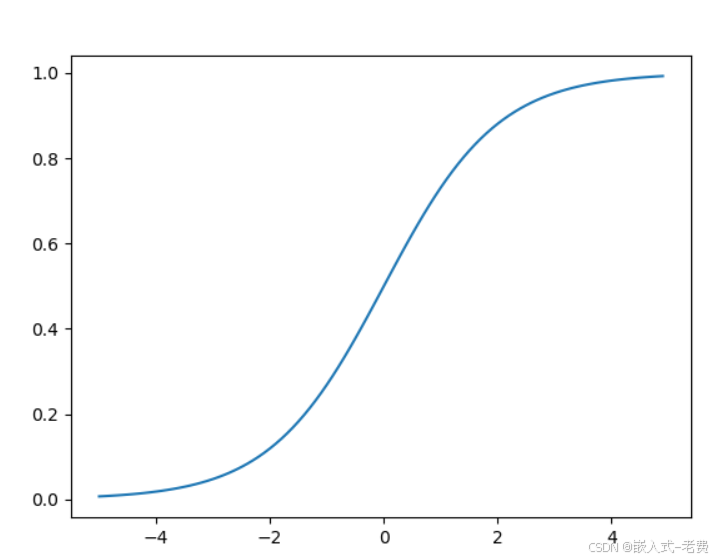
再比如sigmoid函数，

y = 1 / (1 + np.exp(-x))

还比如relu函数

y = max(0, x)

这里面每一个函数都不是很复杂，大家都可以用matplotlib画一下，应该有不少收获。

2、矩阵运算

在神经网络当中，矩阵的运算是少不了的。特别是矩阵的乘法，基本是我们经常会遇到的运算。这里面numpy也提供了对应的操作接口，可以直接拿过来使用。当然大家如果是用c++开发，而不是采用python，那么可以直接使用eigen库来处理，效果也是一样的。

复制代码

import numpy as np

print('Data of A is as follows,')
A=np.array([1,2,3])
print(A.shape)
print(A)

print ('Data of B is as follows,')
B=np.array([[1,2], [3,4], [5,6]])
print(B.shape)
print(B)

print ('Matrix multiply1 is as follows,')
A=np.array([[1,2],[3,4]])
B=np.array([[5,6],[7,8]])
C=np.dot(A,B)
print(C)

print ('Matrix multiply2 is as follows,')
A=np.array([[1,2,3],[4,5,6]])
B=np.array([[1,2],[3,4],[5,6]])
C=np.dot(A,B)
print(C)

3、基本网络的构成

所谓的神经网络，就是输入和输出端之间，不是一个方程可以解决的。这当中，方程套了方程，也就是说，输入和输出之间套了很多的子方程。如果换成神经网络的语言，就是在输入层、输出层之间有很多的隐藏层，即隐藏层1、隐藏层2、隐藏层n等等。我们通过矩阵和sigmoid函数，就可以把这些层都串起来了，这样就构成了一个基础的神经网络。如果写成python代码，就是这样的形式，后一个网络层的输入，就是前一个网络层的输出，

复制代码

'''
full network
'''

def init_network():
    network = {}
    network['W1'] = np.array([[0.1,0.3,0.5], [0.2,0.4,0.6]])
    network['b1'] = np.array([0.1, 0.2, 0.3])
    network['W2'] = np.array([[0.1,0.4], [0.2,0.5],[0.3, 0.6]])
    network['b2'] = np.array([0.1, 0.2])
    network['W3'] = np.array([[0.1,0.3], [0.2,0.4]])
    network['b3'] = np.array([0.1, 0.2])
    return network


def forward(network, x):
    W1,W2,W3 = network['W1'], network['W2'], network['W3']
    b1,b2,b3 = network['b1'], network['b2'], network['b3']
    a1 = np.dot(x, W1)+b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2)+b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3)+b3
    y = identify_function(a3)
    return y

print('network result is as follows,')
network=init_network()
x=np.array([1.0, 0.5])
y=forward(network, x)
print(y)

对应的神经网络形式，其实就是这样的，

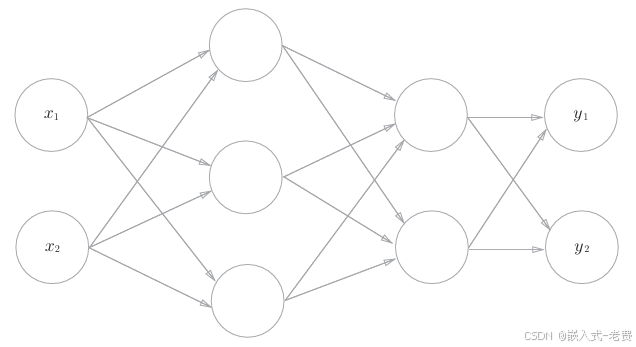
4、调整最后的输出层

输出的结果，我们一般都习惯用softmax转一下再进行处理。首先，对入参做一个exp处理。接着，计算每一个入参对数据之和的百分比，最后输出整个百分比即可。这样看上去也没有什么问题。但一旦数据很大的话，exp得到的结果就更大，所以一般会做一个减法，再重复上面的运算。

复制代码

def softmax(a):
    c=np.max(a)
    exp_a = np.exp(a-c)
    sum_exp_a = np.sum(exp_a)
    y = exp_a/sum_exp_a
    return y