算法 day 46 - 技术栈

回文子串

这个题确实双指针还好理解一些，dp的思想里主要是遍历顺序会不那么容易想到，再者双指针的空间也更优一些。

在dp的遍历顺序中，i是左边的指针，j是右边的指针，他的遍历顺序是从中间往两边扩散的。

cpp 复制代码

class Solution {
public:
    int countSubstrings(string s) {
        int result = 0;
        for (int i = 0; i < s.size(); i++) {
            result += extend(s, i, i, s.size()); // 以i为中心
            result += extend(s, i, i + 1, s.size()); // 以i和i+1为中心
        }
        return result;
    }
    int extend(const string& s, int i, int j, int n) {
        int res = 0;
        while (i >= 0 && j < n && s[i] == s[j]) {
            i--;
            j++;
            res++;
        }
        return res;
    }
};

如上是双指针的写法，i就是从左到右走，j跟着i走，最后遍历完整个字符串，两边扩张，更好理解，这个方法最需要注意的就是单中心和双中心需要分类讨论。

最长回文子序列

和上一题有异曲同工之妙，有上一个题的铺垫，这个题看懂会流畅不少。

cpp 复制代码

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));
        for (int i = 0; i < s.size(); i++) dp[i][i] = 1;
        for (int i = s.size() - 1; i >= 0; i--) {
            for (int j = i + 1; j < s.size(); j++) {
                if (s[i] == s[j]) {
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                } else {
                    dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[0][s.size() - 1];
    }
};

动态规划总结

动规五部曲分别为：

确定dp数组（dp table）以及下标的含义
确定递推公式
dp数组如何初始化
确定遍历顺序
举例推导dp数组

实战中，常常会贪图省事，漏掉最后一步，然后看着wa发呆。每个题有不同的侧重点，可以说步步都很重要吧，以为的捷径，还不如按部就班。

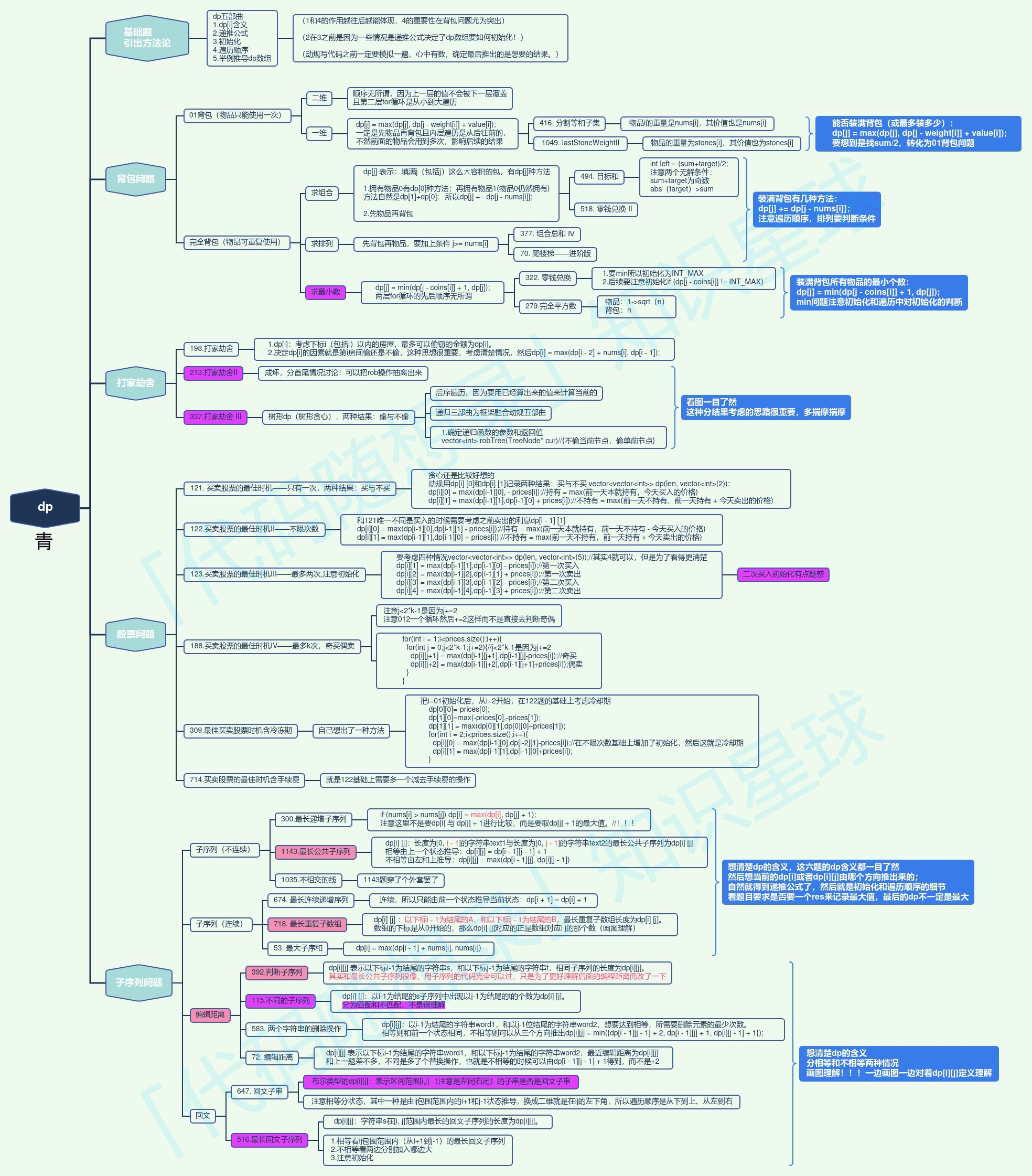
p上引用的思维导图，常看常新，虽然代码这东西，照着写上去的一会儿就忘，但是多看几遍，就会成了自己的了。