基数排序是一种非比较型排序算法,核心思想是「按位分组排序」------ 无需直接比较元素大小,而是按数字的每一位(个位、十位、百位...)或字符的 ASCII 码
其优势是时间复杂度稳定,适合处理大规模数字 / 字符串排序;缺点是依赖数据的 "位结构",且需要额外空间存储桶或计数数组。
算法原理
-
位处理顺序:
-
最低位优先(LSD):先按个位排序,再按十位、百位...(最常用,实现简单)。
-
最高位优先(MSD):先按百位排序,再按十位、个位...(适合部分有序数据,需递归处理)。
-
-
底层排序:每一位的分组排序依赖「计数排序」或「桶排序」(必须是稳定排序,否则会破坏前一位的排序结果)。
-
核心逻辑:每处理一位,元素会按该位的大小初步有序;所有位处理完毕后,整个数组完全有序。
核心思路(以 LSD 为例,升序排序)
原始数组:[18, 94, 215, 789, 17, 934, 71, 85, 70, 147]核心规则:按「个位→十位→百位」逐位排序,每轮用计数排序(稳定排序)分组,最终实现整体升序。
预处理:确定关键参数
- 数组长度
n=10; - 最大元素:789(3 位),因此需处理 3 轮(
d=0个位、d=1十位、d=2百位); - 基数
k=10(数字 0~9),每轮用大小为 10 的计数数组。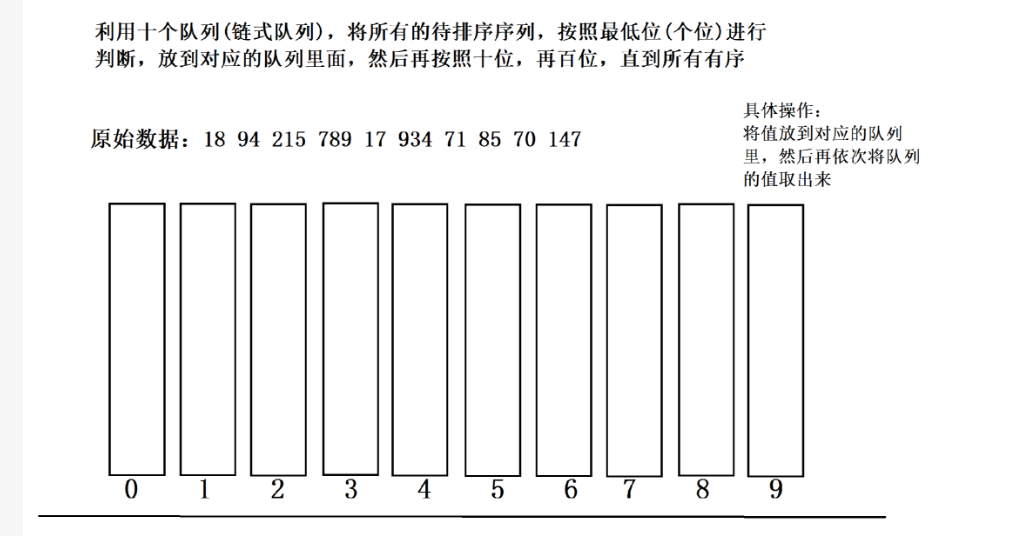
一、第 1 轮排序:按个位(d=0)
步骤 1:获取各位数字
原始数组元素 → 个位数字:18 (8)、94 (4)、215 (5)、789 (9)、17 (7)、934 (4)、71 (1)、85 (5)、70 (0)、147 (7)
步骤 2:计数数组统计次数
初始化计数数组 count[10] = {0},统计每个个位数字的出现次数:
- 0:1 次(70)、1:1 次(71)、4:2 次(94、934)、5:2 次(215、85)、7:2 次(17、147)、8:1 次(18)、9:1 次(789)
- 计数数组结果:
count = [1, 1, 0, 0, 2, 2, 0, 2, 1, 1]
步骤 3:调整计数数组(确定最终位置,保证稳定性)
计数数组累加,存储每个数字的最终结束位置:
count[i] = count[i] + count[i-1](从 i=1 开始)- 调整后:
count = [1, 2, 2, 2, 4, 6, 6, 8, 9, 10]
步骤 4:从后向前填充临时数组(维持稳定性)
临时数组 output[10],按 "原数组逆序 + 计数数组定位" 填充:
| 原数组索引 | 元素 | 个位数字 | 计数数组对应值 | output 索引 | output 数组(填充后) |
|---|---|---|---|---|---|
| 9 | 147 | 7 | count[7]=8 | 7 | [70, 71, 94, 934, 215, 85, 17, 147, 18, 789] |
| 8 | 70 | 0 | count[0]=1 | 0 | |
| 7 | 85 | 5 | count[5]=6 | 5 | |
| 6 | 71 | 1 | count[1]=2 | 1 | |
| 5 | 934 | 4 | count[4]=4 | 3 | |
| 4 | 17 | 7 | count[7]=7 | 6 | |
| 3 | 789 | 9 | count[9]=10 | 9 | |
| 2 | 215 | 5 | count[5]=5 | 4 | |
| 1 | 94 | 4 | count[4]=3 | 2 | |
| 0 | 18 | 8 | count[8]=9 | 8 |
步骤 5:复制回原数组
第 1 轮后数组(个位有序):[70, 71, 94, 934, 215, 85, 17, 147, 18, 789]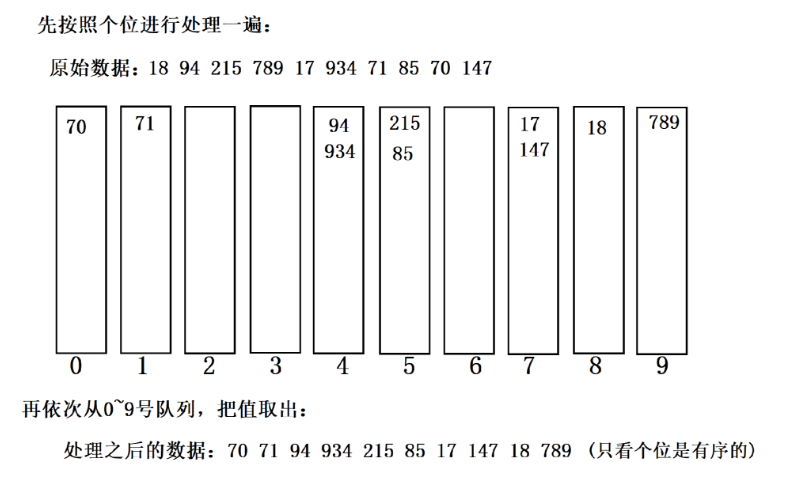
二、第 2 轮排序:按十位(d=1)
步骤 1:获取各位数字
当前数组元素 → 十位数字:70 (7)、71 (7)、94 (9)、934 (3)、215 (1)、85 (8)、17 (1)、147 (4)、18 (1)、789 (8)
步骤 2:计数数组统计次数
count[10] = {0},统计十位数字出现次数:
- 1:3 次(215、17、18)、3:1 次(934)、4:1 次(147)、7:2 次(70、71)、8:2 次(85、789)、9:1 次(94)
- 计数数组结果:
count = [0, 3, 0, 1, 1, 0, 0, 2, 2, 1]
步骤 3:调整计数数组
调整后:count = [0, 3, 3, 4, 5, 5, 5, 7, 9, 10]
步骤 4:从后向前填充临时数组
临时数组 output[10] 填充结果:[17, 18, 215, 934, 147, 70, 71, 85, 789, 94]
步骤 5:复制回原数组
第 2 轮后数组(十位有序):[17, 18,215 ,934, 147, 70, 71, 85, 789, 94]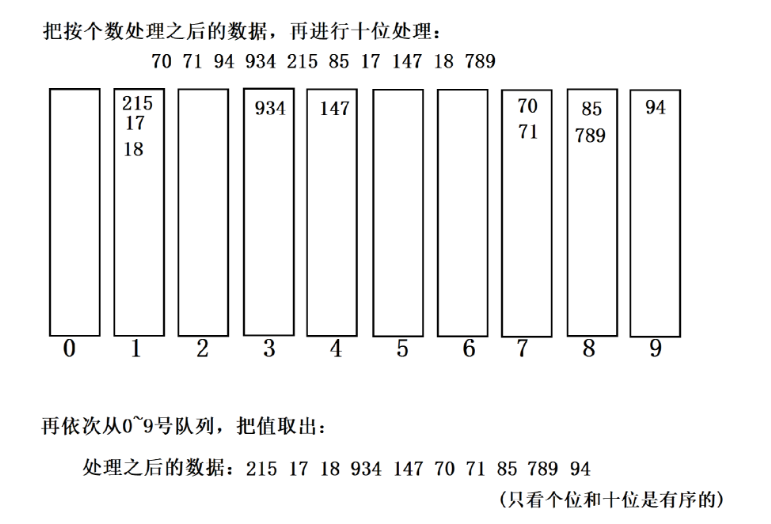
三、第 3 轮排序:按百位(d=2)
步骤 1:获取各位数字
当前数组元素 → 百位数字:17 (0)、18 (0)、215 (2)、934 (9)、147 (1)、70 (0)、71 (0)、85 (0)、789 (7)、94 (0)
步骤 2:计数数组统计次数
count[10] = {0},统计百位数字出现次数:
- 0:6 次(17、18、70、71、85、94)、1:1 次(147)、2:1 次(215)、7:1 次(789)、9:1 次(934)
- 计数数组结果:
count = [6, 1, 1, 0, 0, 0, 0, 1, 0, 1]
步骤 3:调整计数数组
调整后:count = [6, 7, 8, 8, 8, 8, 8, 9, 9, 10]
步骤 4:从后向前填充临时数组
临时数组 output[10] 填充结果:[17, 18, 70, 71, 85, 94, 147, 215, 789, 934]
步骤 5:复制回原数组
第 3 轮后数组(百位有序):[17, 18, 70, 71, 85, 94, 147, 215, 789, 934]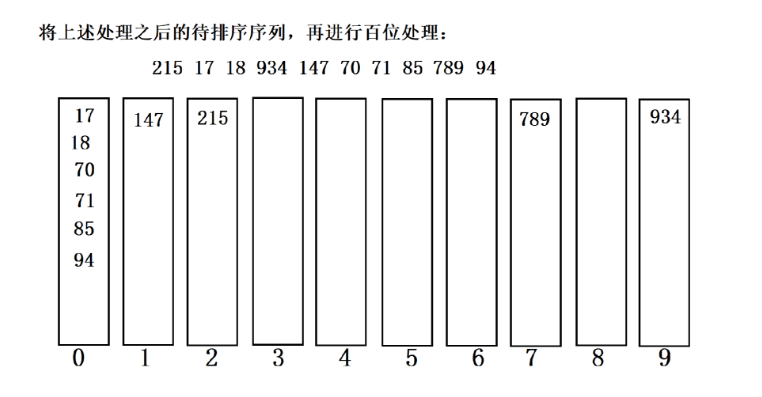
四、最终排序结果
[17, 18, 70, 71, 85, 94, 147, 215, 789, 934]
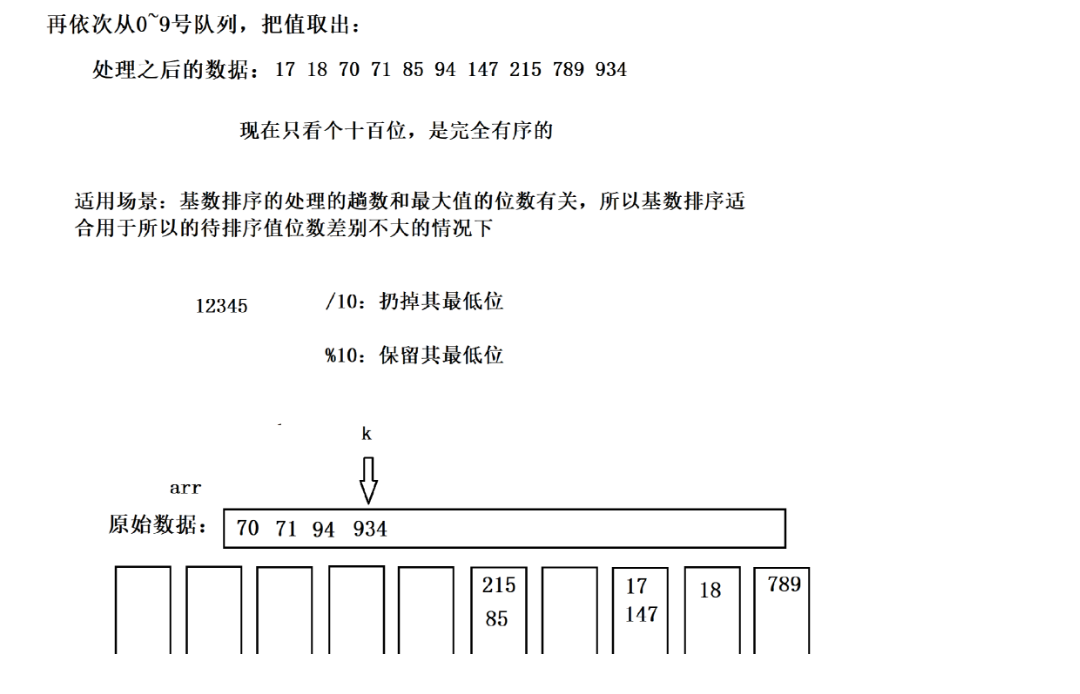
C 语言实现(LSD 基数排序,基于计数排序)
选择「计数排序」作为底层排序(稳定、高效、空间开销小),支持非负整数排序(可扩展至负数、字符串)。
1. 核心辅助函数:获取数字的某一位
cpp
int getmax(int arr[], int len) {
int r = arr[0];
for (int i = 1; i < len; i++) {
if (r < arr[i]) {
r = arr[i];
}
}
return r;
}2. 核心辅助函数:计数排序(按某一位排序)
辅助队列实现:
cpp
void Count_Sort(int arr[], int len, int epfd) {
queue<int> bucket[10];
int* out = (int*)malloc(len * sizeof(int));
for (int i = 0; i < len; i++) {
int index = (arr[i] / epfd) % 10;
bucket[index].push(arr[i]);
}
int r = 0;
for (int i = 0; i < 10; i++) {
while (!bucket[i].empty()) {
arr[r++] = bucket[i].front();
bucket[i].pop();
}
}
}不借助队列:
cpp
void Count_Sort1(int arr[], int len, int epfd) {
int* out = (int*)malloc(len * sizeof(int));
int count[10] = { 0 };
// 步骤1:统计当前位各数字的出现次数
for (int i = 0; i < len; i++) {
count[(arr[i] / epfd) % 10]++;
}
// 步骤2:修改计数数组,使其存储最终位置(保证稳定性)
for (int i = 1; i < 10; i++) {
count[i] += count[i - 1];
}
// 步骤3:从后向前遍历原数组,按当前位放入临时数组(维持稳定性)
for (int i = len - 1; i >= 0; i--) {
int index = (arr[i] / epfd) % 10;
out[count[index] - 1] = arr[i];
count[index]--;
}
// 步骤4:将临时数组复制回原数组
for (int i = 0; i < len; i++) {
arr[i] = out[i];
}
free(out);
out = NULL;
}3.基数排序主函数
cpp
void Radix_Sort(int arr[], int len) {
int max = getmax(arr, len);
for (int epfd = 1; max / epfd > 0; epfd *= 10) {
Count_Sort(arr, len, epfd);
}
}复杂度分析与优缺点
1. 复杂度
| 时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|
| O(d×(n+k)) | O(n+k) | 稳定 |
-
说明:
-
d:最大元素的位数(如 999→d=3); -
n:数组长度; -
k:每一位的基数(数字为 10,字符为 256)。
-
-
实际场景中,
d通常是常数(如整数最多 10 位),因此时间复杂度可近似为 O (n),效率极高。
2. 优缺点
| 核心优点 | 核心缺点 |
|---|---|
| 非比较排序,效率高(近似 O (n)) | 依赖数据结构(仅支持数字、字符串等有 "位" 的数据) |
| 稳定排序(适合多字段排序) | 需要额外空间(临时数组 + 计数数组) |
| 大规模数据排序性能优异 | 不适合小数、负数(需额外处理符号和小数点) |
总结
基数排序的核心是「按位分桶 + 稳定排序」,通过非比较的方式避开了 O (n log n) 的下界,在大规模数字 / 字符串排序中性能优异。其关键是保证底层排序的稳定性,否则会破坏前一位的排序结果。