Transformer架构：手撸源码实践(附带仓库地址)

黑唐僧2025-11-10 10:48

Transformer架构：手撸源码实践

1. 引言

Transformer架构自2017年在论文《Attention Is All You Need》中被提出以来，彻底改变了自然语言处理（NLP）领域。它摒弃了传统的循环神经网络（RNN）和卷积神经网络（CNN），完全基于注意力机制构建，成为现代大语言模型（如BERT、GPT系列）的基础架构。

本文将深入解析Transformer的核心组件，通过手写实现代码来帮助理解其内部工作机制。

2. Transformer整体架构

Transformer采用经典的编码器-解码器架构：

复制代码 
输入序列 → 编码器 → 解码器 → 输出序列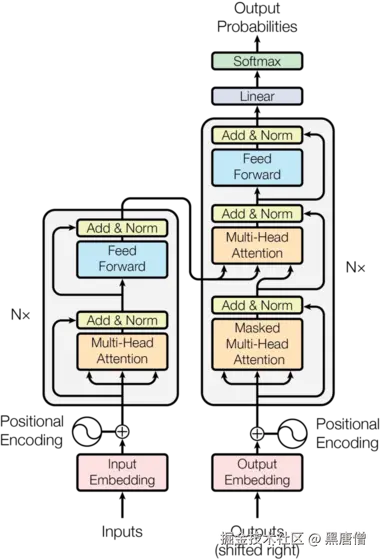

2.1 编码器（Encoder）

编码器由6个相同的层堆叠而成，每层包含两个子层：

  1. 多头自注意力机制（Multi-Head Self-Attention）
  2. 位置前馈网络（Position-wise Feed-Forward Networks）

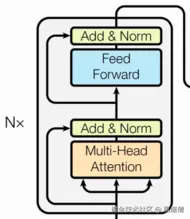每层都使用残差连接和层归一化。

编码器可以表示为以下公式：

<math xmlns="http://www.w3.org/1998/Math/MathML"> E n c L a y e r ( x ) = L a y e r N o r m ( x + S e l f A t t e n t i o n ( x ) ) \mathrm{EncLayer}(x) = \mathrm{LayerNorm}(x + \mathrm{SelfAttention}(x)) </math>EncLayer(x)=LayerNorm(x+SelfAttention(x))

<math xmlns="http://www.w3.org/1998/Math/MathML"> E n c L a y e r ( x ) = L a y e r N o r m ( x + F F N ( x ) ) \mathrm{EncLayer}(x) = \mathrm{LayerNorm}(x + \mathrm{FFN}(x)) </math>EncLayer(x)=LayerNorm(x+FFN(x))

完整的编码器层可以表示为：

<math xmlns="http://www.w3.org/1998/Math/MathML"> E n c o d e r L a y e r ( x ) = L a y e r N o r m ( L a y e r N o r m ( x + S e l f A t t e n t i o n ( x ) ) + F F N ( L a y e r N o r m ( x + S e l f A t t e n t i o n ( x ) ) ) ) \mathrm{EncoderLayer}(x) = \mathrm{LayerNorm}(\mathrm{LayerNorm}(x + \mathrm{SelfAttention}(x)) + \mathrm{FFN}(\mathrm{LayerNorm}(x + \mathrm{SelfAttention}(x)))) </math>EncoderLayer(x)=LayerNorm(LayerNorm(x+SelfAttention(x))+FFN(LayerNorm(x+SelfAttention(x))))

2.2 解码器（Decoder）

解码器也由6个相同的层堆叠而成，每层包含三个子层：

  1. 掩码多头自注意力机制（Masked Multi-Head Self-Attention）
  2. 编码器-解码器注意力机制（Encoder-Decoder Attention）
  3. 位置前馈网络（Position-wise Feed-Forward Networks）

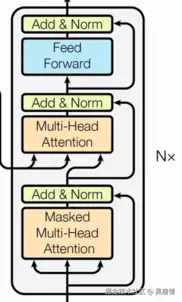同样，每层都使用残差连接和层归一化。

解码器层可以表示为以下公式：

<math xmlns="http://www.w3.org/1998/Math/MathML"> D e c L a y e r ( x , e n c o u t ) = L a y e r N o r m ( x + M a s k e d S e l f A t t e n t i o n ( x ) ) \mathrm{DecLayer}(x, enc_out) = \mathrm{LayerNorm}(x + \mathrm{MaskedSelfAttention}(x)) </math>DecLayer(x,encout)=LayerNorm(x+MaskedSelfAttention(x))

<math xmlns="http://www.w3.org/1998/Math/MathML"> D e c L a y e r ( x , e n c o u t ) = L a y e r N o r m ( x + E n c o d e r A t t e n t i o n ( x , e n c o u t ) ) \mathrm{DecLayer}(x, enc_out) = \mathrm{LayerNorm}(x + \mathrm{EncoderAttention}(x, enc_out)) </math>DecLayer(x,encout)=LayerNorm(x+EncoderAttention(x,encout))

<math xmlns="http://www.w3.org/1998/Math/MathML"> D e c L a y e r ( x , e n c o u t ) = L a y e r N o r m ( x + F F N ( x ) ) \mathrm{DecLayer}(x, enc_out) = \mathrm{LayerNorm}(x + \mathrm{FFN}(x)) </math>DecLayer(x,encout)=LayerNorm(x+FFN(x))

3. 核心组件详解

3.1 注意力机制（Attention）

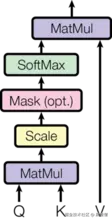
注意力机制是Transformer的核心，其数学表达式为：

<math xmlns="http://www.w3.org/1998/Math/MathML"> Attention ( Q , K , V ) = softmax ( Q K T d k ) V \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V </math>Attention(Q,K,V)=softmax(dk QKT)V

其中：

  • Q（Query）：查询向量
  • K（Key）：键向量
  • V（Value）：值向量
  • <math xmlns="http://www.w3.org/1998/Math/MathML"> d k d_k </math>dk：键向量的维度

缩放因子 <math xmlns="http://www.w3.org/1998/Math/MathML"> 1 d k \frac{1}{\sqrt{d_k}} </math>dk 1的作用是为了防止点积结果过大导致softmax函数梯度消失。

在我们的实现中，注意力机制的代码如下：

python 复制代码 
def attention(q, k, v, mask=None, dropout=None):
    """
    计算注意力机制
    
    Args:
        q: 查询矩阵 [batch_size, heads, seq_len, d_k]
        k: 键矩阵 [batch_size, heads, seq_len, d_k]
        v: 值矩阵 [batch_size, heads, seq_len, d_k]
        mask: 掩码矩阵，用于屏蔽某些位置
        dropout: dropout层
    
    Returns:
        tuple: (注意力输出, 注意力权重)
    """
    # 自注意力公式三步走

    # 第一步: q* k的转置除以根号d_k

    # 第二部: 判断是否做掩码, softmax层计算

    # 第三部: 乘以V
    # [batch_size, sqen_len, embed_dim]
    embed_dim = k.size(-1)
    # 计算Q和K的点积 [batch_size, heads, seq_len, seq_len]
    q_k = torch.matmul(q, k.transpose(-1,-2)) # batch_size, sqen_len, sqen_len
    # 缩放点积，除以根号d_k，防止梯度消失
    attn_weight = q_k / math.sqrt(embed_dim)

    if mask is not None:
        # 使用mask屏蔽不需要关注的位置，将被屏蔽位置的权重设为极小值
        attn_weight = attn_weight.masked_fill(mask == 0, -1e9)

    # 对注意力权重进行softmax归一化
    attn_weight = nn.functional.softmax(attn_weight, dim=-1)

    if dropout is not None:
        # 应用dropout防止过拟合
        attn_weight = dropout(attn_weight)

    # 使用注意力权重对V进行加权求和
    res = torch.matmul(attn_weight , v)

    return res, attn_weight

3.2 多头注意力（Multi-Head Attention）

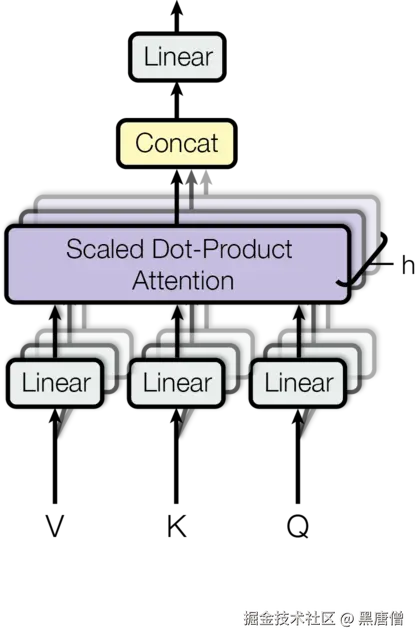
为了增强模型捕捉不同位置信息的能力，Transformer使用多头注意力机制：

<math xmlns="http://www.w3.org/1998/Math/MathML"> MultiHead ( Q , K , V ) = Concat ( head 1 , . . . , head h ) W O \text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, ..., \text{head}_h)W^O </math>MultiHead(Q,K,V)=Concat(head1,...,headh)WO

其中每个头计算为： <math xmlns="http://www.w3.org/1998/Math/MathML"> head i = Attention ( Q W i Q , K W i K , V W i V ) \text{head}_i = \text{Attention}(QW_i^Q, KW_i^K, VW_i^V) </math>headi=Attention(QWiQ,KWiK,VWiV)

多头注意力机制允许模型在不同表示子空间中并行关注信息，增强了模型的表达能力。

MultiHead计算的完整过程可以表示为：

<math xmlns="http://www.w3.org/1998/Math/MathML"> M u l t i H e a d ( Q , K , V ) = C o n c a t ( h e a d 1 , . . . , h e a d h ) W O \mathrm{MultiHead}(Q, K, V) = \mathrm{Concat}(\mathrm{head_1}, ..., \mathrm{head_h})W^O </math>MultiHead(Q,K,V)=Concat(head1,...,headh)WO

<math xmlns="http://www.w3.org/1998/Math/MathML"> where h e a d i = A t t e n t i o n ( Q W i Q , K W i K , V W i V ) \text{where} \quad \mathrm{head_i} = \mathrm{Attention}(QW_i^Q, KW_i^K, VW_i^V) </math>whereheadi=Attention(QWiQ,KWiK,VWiV)

多头注意力机制结构图
python 复制代码 
class MultiHeadAttention(nn.Module):
    """
    多头注意力机制
    将输入分割为多个头，分别计算注意力，然后合并结果
    """
    def __init__(self, heads, embed_dim, dropout_p=0.1):
        """
        初始化多头注意力
        
        Args:
            heads: 注意力头的数量
            embed_dim: 嵌入维度
            dropout_p: dropout概率
        """
        super().__init__()
        # 构建属性
        self.heads = heads
        self.embed_dim = embed_dim

        # 确保嵌入维度可以被头数整除
        assert embed_dim % heads  == 0
        # 计算每个头的维度
        self.d_k = embed_dim // heads
        # 构建4个线性层: 3个用于Q、K、V的线性变换，1个用于最终输出
        self.linears = clone_modules(nn.Linear(embed_dim, embed_dim), 4)
        # 实例化dropout
        self.dropout = nn.Dropout(dropout_p)

    def forward(self, q, k, v, mask=None):
        """
        前向传播
        
        Args:
            q: 查询 [batch_size, seq_len, embed_dim]
            k: 键 [batch_size, seq_len, embed_dim]
            v: 值 [batch_size, seq_len, embed_dim]
            mask: 掩码矩阵
        
        Returns:
            torch.Tensor: 多头注意力输出
        """
        if mask is not None:
            # 扩展mask的维度以匹配多头
            mask = mask.unsqueeze(0)
        batch_size = q.size(0)
        heads = self.heads
        embed_dim = q.size(-1)
        d_k = self.d_k
        # 拆分多头序列 + 做线性变换
        # 对Q、K、V分别应用线性变换，然后reshape为(batch_size, heads, seq_len, d_k)
        q, k, v = [linear(x)
                    .view(batch_size, -1, heads, d_k)
                    .transpose(1,2)
                    for linear,x in zip(self.linears,(q,k,v))]

        # 获取注意力机制输出
        output, attn_weight = attention(q, k, v, mask, self.dropout)
        # 合并多头到一个量中
        # 交换维度并合并heads和d_k维度
        res = output.transpose(1,2).contiguous().view(batch_size, -1, embed_dim)
        # 最后使用线性层做收尾处理
        return self.linears[-1](res)

3.3 位置编码（Positional Encoding）

由于自注意力机制本身不包含位置信息，Transformer引入位置编码来为模型提供序列中词的位置信息。

Transformer使用正弦和余弦函数生成位置编码：

<math xmlns="http://www.w3.org/1998/Math/MathML"> P E ( p o s , 2 i ) = sin ⁡ ( p o s 1000 0 2 i / d model ) PE_{(pos,2i)} = \sin\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right) </math>PE(pos,2i)=sin(100002i/dmodelpos)

<math xmlns="http://www.w3.org/1998/Math/MathML"> P E ( p o s , 2 i + 1 ) = cos ⁡ ( p o s 1000 0 2 i / d model ) PE_{(pos,2i+1)} = \cos\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right) </math>PE(pos,2i+1)=cos(100002i/dmodelpos)

其中：

  • <math xmlns="http://www.w3.org/1998/Math/MathML"> p o s pos </math>pos 是位置
  • <math xmlns="http://www.w3.org/1998/Math/MathML"> i i </math>i 是维度
  • <math xmlns="http://www.w3.org/1998/Math/MathML"> d model d_{\text{model}} </math>dmodel 是模型维度

这种设计使得模型能够学习到相对位置信息，因为对于任意固定的偏移 <math xmlns="http://www.w3.org/1998/Math/MathML"> k k </math>k， <math xmlns="http://www.w3.org/1998/Math/MathML"> P E p o s + k PE_{pos+k} </math>PEpos+k 可以表示为 <math xmlns="http://www.w3.org/1998/Math/MathML"> P E p o s PE_{pos} </math>PEpos 的线性函数。

位置编码的完整公式可以表示为：

<math xmlns="http://www.w3.org/1998/Math/MathML"> P E ( p o s , 2 i ) = sin ⁡ ( p o s 1000 0 2 i / d model ) PE_{(pos,2i)} = \sin\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right) </math>PE(pos,2i)=sin(100002i/dmodelpos)

<math xmlns="http://www.w3.org/1998/Math/MathML"> P E ( p o s , 2 i + 1 ) = cos ⁡ ( p o s 1000 0 2 i / d model ) PE_{(pos,2i+1)} = \cos\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right) </math>PE(pos,2i+1)=cos(100002i/dmodelpos)

python 复制代码 
class PositionalEmbedding(nn.Module):
    """
    位置编码层
    为序列中每个位置生成独特的编码，使模型能够利用序列顺序信息
    """
    def __init__(self, max_length, embed_dim, dropout_p=0.1):
        """
        初始化位置编码层
        
        Args:
            max_length: 序列最大长度
            embed_dim: 嵌入维度
            dropout_p: dropout概率
        """
        super().__init__()
        self.max_length = max_length
        self.embed_dim = embed_dim

        # Dropout层用于防止过拟合
        self.dropout = nn.Dropout(p=dropout_p)

        # 创建位置编码矩阵 [max_length, embed_dim]
        pe = torch.zeros(max_length, embed_dim)   # [60, 512]
        
        # 生成位置信息 [max_length, 1]
        pos = torch.arange(0, max_length).unsqueeze(1) # [60, 1] = [[0],[1],[2], ...[59]]
        # 生成维度索引 0, 2, 4, ..., embed_dim-2 （只取偶数索引）
        tow_i = torch.arange(0, embed_dim, 2) # [256] = 0 2 4 6 8 .. 510  , 一共256个数
        # 计算角度频率参数
        tmp_v = torch.exp((math.log(10000) * -tow_i / self.embed_dim)) # [256]

        # 计算角度值：pos * 角度频率
        fn_v = tmp_v * pos # [256] * [60, 1]

        # 偶数位置使用sin编码
        pe[:, 0::2] = torch.sin(fn_v)
        # 奇数位置使用cos编码
        pe[:, 1::2] = torch.cos(fn_v)

        # 增加batch维度 [1, max_length, embed_dim]
        pe = pe.unsqueeze(0) # [1, 60, 512]

        # 注册为buffer，不会被更新，但会随模型保存和加载
        self.register_buffer('pe', pe)

    def forward(self, x): # 输入形状：[batch_size, seq_len, embed_dim]
        """
        前向传播
        
        Args:
            x: 输入张量 [batch_size, seq_len, embed_dim]
        
        Returns:
            torch.Tensor: 加入位置编码的张量 [batch_size, seq_len, embed_dim]
        """
        # 截取与输入序列长度相等的位置编码
        p_x = self.pe[:, :x.size(1)] # [1, seq_len, embed_dim]
        # 将位置编码与输入相加，并应用dropout
        res = self.dropout(p_x + x) # [batch_size, seq_len, embed_dim]

        return res

3.4 词嵌入与缩放（Embedding and Scaling）

Transformer中的Embedding层负责将离散的词汇转换为连续向量表示。为了保持数值稳定性，Transformer在词嵌入后进行缩放操作：

<math xmlns="http://www.w3.org/1998/Math/MathML"> Embedding scaled = Embedding × d model \text{Embedding}{\text{scaled}} = \text{Embedding} \times \sqrt{d{\text{model}}} </math>Embeddingscaled=Embedding×dmodel

词嵌入缩放的目的是平衡词嵌入和位置编码的数值范围，确保两者在数值上处于相近的量级，有助于模型训练的稳定性。

python 复制代码 
class Embeddings(nn.Module):
    """
    词嵌入层
    将词汇索引转换为密集向量表示
    """
    def __init__(self, input_size, embed_dim):
        """
        初始化词嵌入层
        
        Args:
            input_size: 词汇表大小
            embed_dim: 嵌入维度
        """
        super().__init__()
        self.embed_dim = embed_dim
        # 创建嵌入层，将input_size个单词映射到embed_dim维向量
        self.embed = nn.Embedding(input_size, embedding_dim=embed_dim)

    def forward(self, x):
        """
        前向传播
        
        Args:
            x: 输入张量，包含词汇索引 [batch_size, seq_len]
        
        Returns:
            torch.Tensor: 词嵌入向量 [batch_size, seq_len, embed_dim]
        """
        # 通过嵌入层获取向量表示，并除以sqrt(embed_dim)进行缩放
        # 这种缩放有助于稳定梯度，特别是在位置编码加入之后
        return self.embed(x) / math.sqrt(self.embed_dim)

3.5 层归一化（Layer Normalization）

层归一化用于稳定训练过程，加速收敛。其数学公式为：

<math xmlns="http://www.w3.org/1998/Math/MathML"> μ = 1 H ∑ i = 1 H x i \mu = \frac{1}{H}\sum_{i=1}^{H} x_i </math>μ=H1∑i=1Hxi

<math xmlns="http://www.w3.org/1998/Math/MathML"> σ 2 = 1 H ∑ i = 1 H ( x i − μ ) 2 \sigma^2 = \frac{1}{H}\sum_{i=1}^{H} (x_i - \mu)^2 </math>σ2=H1∑i=1H(xi−μ)2

<math xmlns="http://www.w3.org/1998/Math/MathML"> y = x − μ σ 2 + ϵ ⊙ γ + β y = \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}} \odot \gamma + \beta </math>y=σ2+ϵ x−μ⊙γ+β

其中：

  • <math xmlns="http://www.w3.org/1998/Math/MathML"> μ \mu </math>μ 是均值
  • <math xmlns="http://www.w3.org/1998/Math/MathML"> σ 2 \sigma^2 </math>σ2 是方差
  • <math xmlns="http://www.w3.org/1998/Math/MathML"> ϵ \epsilon </math>ϵ 是一个小常数，防止除零
  • <math xmlns="http://www.w3.org/1998/Math/MathML"> γ \gamma </math>γ 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> β \beta </math>β 是可学习的缩放和偏移参数

层归一化的完整计算过程可以表示为：

<math xmlns="http://www.w3.org/1998/Math/MathML"> L a y e r N o r m ( x ) = x − μ σ 2 + ϵ ⊙ γ + β \mathrm{LayerNorm}(x) = \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}} \odot \gamma + \beta </math>LayerNorm(x)=σ2+ϵ x−μ⊙γ+β

python 复制代码 
class LayerNorm(nn.Module):
    """
    层归一化
    对每个样本的特征进行归一化，而不是对批次维度进行归一化
    """
    def __init__(self, embed_dim, eps=1e-6):
        """
        初始化层归一化
        
        Args:
            embed_dim: 嵌入维度
            eps: 防止除零的小值
        """
        super().__init__()
        # 创建可学习的缩放参数W，初始化为全1矩阵
        self.w = nn.Parameter(torch.ones(embed_dim))
        # 创建可学习的偏移参数B，初始化为全0矩阵
        self.b = nn.Parameter(torch.zeros(embed_dim))
        # 防止除零的小值
        self.eps = eps

    def forward(self, x):
        """
        前向传播
        
        Args:
            x: 输入张量 [batch_size, seq_len, embed_dim]
        
        Returns:
            torch.Tensor: 归一化后的张量
        """
        # 计算平均数
        x_mean = torch.mean(x, keepdim=True, dim=-1) # keepdim=True , 保持形状一致
        # 计算标准差
        x_std = torch.std(x, keepdim=True, dim=-1)
        # 计算 (x-平均数) / (标准差+eps) = 标准化后的x
        res = (x - x_mean) / (x_std + self.eps)  # 修正了原代码中的运算符优先级问题
        # 返回 W * x + b，应用可学习的缩放和偏移
        return self.w * res + self.b

3.6 前馈神经网络（Feed-Forward Networks）

前馈网络对每个位置的表示进行非线性变换。其数学公式为：

<math xmlns="http://www.w3.org/1998/Math/MathML"> F F N ( x ) = max ⁡ ( 0 , x W 1 + b 1 ) W 2 + b 2 \mathrm{FFN}(x) = \max(0, xW_1 + b_1)W_2 + b_2 </math>FFN(x)=max(0,xW1+b1)W2+b2

其中：

  • <math xmlns="http://www.w3.org/1998/Math/MathML"> W 1 ∈ R d m o d e l × d f f W_1 \in \mathbb{R}^{d_{model} \times d_{ff}} </math>W1∈Rdmodel×dff 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> W 2 ∈ R d f f × d m o d e l W_2 \in \mathbb{R}^{d_{ff} \times d_{model}} </math>W2∈Rdff×dmodel 是参数矩阵
  • <math xmlns="http://www.w3.org/1998/Math/MathML"> b 1 b_1 </math>b1 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> b 2 b_2 </math>b2 是偏置向量
  • <math xmlns="http://www.w3.org/1998/Math/MathML"> d f f = 2048 d_{ff} = 2048 </math>dff=2048 是前馈网络的隐藏层维度

前馈网络的完整计算过程可以表示为：

<math xmlns="http://www.w3.org/1998/Math/MathML"> F F N ( x ) = R e L U ( x W 1 + b 1 ) W 2 + b 2 \mathrm{FFN}(x) = \mathrm{ReLU}(xW_1 + b_1)W_2 + b_2 </math>FFN(x)=ReLU(xW1+b1)W2+b2

python 复制代码 
class FeedForward(nn.Module):
    """
    前馈神经网络
    在Transformer中用于对每个位置的表示进行非线性变换
    """
    def __init__(self, embed_dim, hidden_size=2048, dropout_p = 0.1):
        """
        初始化前馈网络
        
        Args:
            embed_dim: 嵌入维度
            hidden_size: 隐藏层大小，默认为2048
            dropout_p: dropout概率
        """
        super().__init__()
        # 两个线性层, 外加ReLU激活函数和dropout随机失活
        # 第一个线性层将维度从embed_dim扩展到hidden_size
        self.linear1 = nn.Linear(embed_dim, hidden_size)

        # ReLU激活函数
        self.relu = nn.ReLU()

        # Dropout层用于防止过拟合
        self.dropout = nn.Dropout(p=dropout_p)

        # 第二个线性层将维度从hidden_size压缩回embed_dim
        self.linear2 = nn.Linear(hidden_size, embed_dim)

    def forward(self, x):
        """
        前向传播
        
        Args:
            x: 输入张量 [batch_size, seq_len, embed_dim]
        
        Returns:
            torch.Tensor: 前馈网络输出
        """
        # 第一层线性变换
        x = self.linear1(x)

        # ReLU激活
        x = self.relu(x)

        # Dropout防止过拟合
        x = self.dropout(x)

        # 第二层线性变换
        x = self.linear2(x)

        return x

3.7 子层连接（Sublayer Connection）

子层连接实现残差连接和层归一化。其数学公式为：

<math xmlns="http://www.w3.org/1998/Math/MathML"> S u b l a y e r ( x ) = L a y e r N o r m ( x + S u b l a y e r ( x ) ) \mathrm{Sublayer}(x) = \mathrm{LayerNorm}(x + \mathrm{Sublayer}(x)) </math>Sublayer(x)=LayerNorm(x+Sublayer(x))

其中Sublayer(x)可以是自注意力层或前馈网络层。

子层连接的完整计算过程可以表示为：

<math xmlns="http://www.w3.org/1998/Math/MathML"> S u b l a y e r C o n n e c t i o n ( x , S u b l a y e r ) = L a y e r N o r m ( x + D r o p o u t ( S u b l a y e r ( x ) ) ) \mathrm{SublayerConnection}(x, \mathrm{Sublayer}) = \mathrm{LayerNorm}(x + \mathrm{Dropout}(\mathrm{Sublayer}(x))) </math>SublayerConnection(x,Sublayer)=LayerNorm(x+Dropout(Sublayer(x)))

python 复制代码 
class SubLayers(nn.Module):
    """
    子层连接模块
    实现残差连接和层归一化
    """
    def __init__(self, embed_dim, dropout_p=0.1):
        """
        初始化子层连接
        
        Args:
            embed_dim: 嵌入维度
            dropout_p: dropout概率
        """
        super().__init__()
        # 实例化层归一化函数
        self.norm = LayerNorm(embed_dim)

        # Dropout层
        self.dropout = nn.Dropout(p=dropout_p)

    def forward(self, x, layer_fn):
        """
        前向传播
        
        Args:
            x: 输入张量
            layer_fn: 要应用的层函数（如注意力层或前馈网络）
        
        Returns:
            torch.Tensor: 经过残差连接和层归一化的输出
        """
        # 对输入应用指定的层函数，然后进行层归一化和dropout
        # 最后与原始输入进行残差连接（x + res）
        res  = self.dropout(self.norm(layer_fn(x)))
        return x + res

4. 编码器实现

编码器由多个编码器层堆叠而成：

编码器层的完整计算过程可以表示为：

<math xmlns="http://www.w3.org/1998/Math/MathML"> E n c o d e r L a y e r ( x ) = S u b l a y e r C o n n e c t i o n ( S u b l a y e r C o n n e c t i o n ( x , S e l f A t t e n t i o n ) , F F N ) \mathrm{EncoderLayer}(x) = \mathrm{SublayerConnection}(\mathrm{SublayerConnection}(x, \mathrm{SelfAttention}), \mathrm{FFN}) </math>EncoderLayer(x)=SublayerConnection(SublayerConnection(x,SelfAttention),FFN)

编码器的完整计算过程可以表示为：

<math xmlns="http://www.w3.org/1998/Math/MathML"> E n c o d e r ( x ) = L a y e r N o r m ( E n c o d e r L a y e r N ( ⋯ ( E n c o d e r L a y e r 1 ( x ) ) ⋯   ) ) \mathrm{Encoder}(x) = \mathrm{LayerNorm}(\mathrm{EncoderLayer}_N(\cdots(\mathrm{EncoderLayer}_1(x))\cdots)) </math>Encoder(x)=LayerNorm(EncoderLayerN(⋯(EncoderLayer1(x))⋯))

python 复制代码 
class EncoderLayer(nn.Module):
    """
    编码器层
    包含自注意力层和前馈神经网络层
    """
    def __init__(self, embed_dim, heads, dropout_p=0.1, hidden_size=2048):
        """
        初始化编码器层
        
        Args:
            embed_dim: 嵌入维度
            heads: 注意力头数
            dropout_p: dropout概率
            hidden_size: 前馈网络隐藏层大小
        """
        super().__init__()

        # 多头自注意力机制
        self.multi_head_attn = MultiHeadAttention(heads=heads, embed_dim=embed_dim, dropout_p=dropout_p)

        # 前馈神经网络
        self.feed_ward = FeedForward(embed_dim=embed_dim, hidden_size=hidden_size, dropout_p=dropout_p)

        # 两个子层连接模块：自注意力和前馈网络
        self.layers = clone_modules(SubLayers(embed_dim=embed_dim, dropout_p=dropout_p), N=2)

    def forward(self, x, mask=None):
        """
        前向传播
        
        Args:
            x: 输入张量 [batch_size, seq_len, embed_dim]
            mask: 掩码张量，用于屏蔽无效位置
        
        Returns:
            torch.Tensor: 编码器层输出
        """
        # 第一层：自注意力机制
        x = self.layers[0](x, lambda x: self.multi_head_attn(x, x, x, mask))

        # 第二层：前馈神经网络
        x = self.layers[1](x, self.feed_ward)
        
        return x

class Encoder(nn.Module):
    """
    编码器
    由多个编码器层堆叠组成
    """
    def __init__(self, embed_dim, layer, N):
        """
        初始化编码器
        
        Args:
            embed_dim: 嵌入维度
            layer: 编码器层模板
            N: 编码器层数
        """
        super().__init__()

        # 克隆N个相同的编码器层
        self.encoder_layers = clone_modules(layer, N)

        # 输出层归一化
        self.norm = LayerNorm(embed_dim=embed_dim)

    def forward(self, x, mask=None):
        """
        前向传播
        
        Args:
            x: 输入张量 [batch_size, seq_len, embed_dim]
            mask: 掩码张量
        
        Returns:
            torch.Tensor: 编码器输出
        """
        # 依次通过每个编码器层
        for layer in self.encoder_layers:
            x = layer(x, mask=mask)
        # 最终层归一化
        res = self.norm(x)
        return res

5. 解码器实现

5.1 解码器实现

解码器也由多个解码器层堆叠而成，但结构比编码器更复杂：

解码器层的完整计算过程可以表示为：

<math xmlns="http://www.w3.org/1998/Math/MathML"> D e c o d e r L a y e r ( x , e n c o u t ) = S u b l a y e r C o n n e c t i o n ( S u b l a y e r C o n n e c t i o n ( S u b l a y e r C o n n e c t i o n ( x , M a s k e d S e l f A t t e n t i o n ) , E n c o d e r A t t e n t i o n ) , F F N ) \mathrm{DecoderLayer}(x, enc_out) = \mathrm{SublayerConnection}(\mathrm{SublayerConnection}(\mathrm{SublayerConnection}(x, \mathrm{MaskedSelfAttention}), \mathrm{EncoderAttention}), \mathrm{FFN}) </math>DecoderLayer(x,encout)=SublayerConnection(SublayerConnection(SublayerConnection(x,MaskedSelfAttention),EncoderAttention),FFN)

解码器的完整计算过程可以表示为：

<math xmlns="http://www.w3.org/1998/Math/MathML"> D e c o d e r ( x , e n c o u t ) = L a y e r N o r m ( D e c o d e r L a y e r N ( ⋯ ( D e c o d e r L a y e r 1 ( x , e n c o u t ) ) ⋯   ) ) \mathrm{Decoder}(x, enc_out) = \mathrm{LayerNorm}(\mathrm{DecoderLayer}_N(\cdots(\mathrm{DecoderLayer}_1(x, enc_out))\cdots)) </math>Decoder(x,encout)=LayerNorm(DecoderLayerN(⋯(DecoderLayer1(x,encout))⋯))

python 复制代码 
class DecoderLayer(nn.Module):
    """
    解码器层
    包含自注意力层、编码器-解码器注意力层和前馈网络
    """
    def __init__(self, embed_dim, heads, feed_forward_hidden_size, dropout_p=0.1):
        """
        初始化解码器层
        
        Args:
            embed_dim: 嵌入维度
            heads: 注意力头数
            feed_forward_hidden_size: 前馈网络隐藏层大小
            dropout_p: dropout概率
        """
        super().__init__()
        # 第一个自注意力机制：目标序列的自注意力（需要掩码）
        self.multi_head_attn = MultiHeadAttention(heads=heads, embed_dim=embed_dim, dropout_p=dropout_p)
        # 三个子层连接模块：自注意力、编码器-解码器注意力、前馈网络
        self.layers = clone_modules(SubLayers(embed_dim=embed_dim, dropout_p=dropout_p), N=3)

        # 前馈神经网络
        self.feed_forward = FeedForward(embed_dim=embed_dim, dropout_p=dropout_p, hidden_size=feed_forward_hidden_size)

    def forward(self, q, k, v, target_mask=None, source_mask=None):
        """
        前向传播
        
        Args:
            q: 查询向量（目标序列）
            k: 键向量（编码器输出）
            v: 值向量（编码器输出）
            target_mask: 目标序列掩码（防止未来信息泄露）
            source_mask: 源序列掩码
        
        Returns:
            torch.Tensor: 解码器层输出
        """
        # 第一层：目标序列的自注意力（使用target_mask防止看到未来信息）
        res_1 = self.layers[0](q, lambda x: self.multi_head_attn(x, x, x, target_mask))

        # 第二层：编码器-解码器注意力（查询来自前一层，键值来自编码器输出）
        res_2 = self.layers[1](res_1, lambda x: self.multi_head_attn(x, k, v, source_mask))

        # 第三层：前馈神经网络
        res_3 = self.layers[2](res_2, self.feed_forward)

        return res_3

class Decoder(nn.Module):
    """
    解码器
    由多个解码器层堆叠而成
    """
    def __init__(self, embed_dim, decoder_layer, n):
        """
        初始化解码器
        
        Args:
            embed_dim: 嵌入维度
            decoder_layer: 解码器层模板
            n: 解码器层数
        """
        super().__init__()
        # 输出层归一化
        self.norm = LayerNorm(embed_dim=embed_dim)

        # 克隆N个解码器层
        self.encoder_layers = clone_modules(decoder_layer, n)

    def forward(self, q, k, v, target_mask=None, source_mask=None):
        """
        前向传播
        
        Args:
            q: 查询向量（目标序列）
            k: 键向量（编码器输出）
            v: 值向量（编码器输出）
            target_mask: 目标序列掩码
            source_mask: 源序列掩码
        
        Returns:
            torch.Tensor: 解码器输出
        """
        # 初始输入为查询向量
        res = q
        # 依次通过每个解码器层
        for layer in self.encoder_layers:
            res = layer(q, k, v, target_mask, source_mask)

        # 最终层归一化
        res = self.norm(res)

        return res

5.2输出部分介绍

输出部分包含: * 线性层 * softmax层

5.2.1 线性层的作用
  • 通过对上一步的线性变化得到指定维度的输出, 也就是转换维度的作用.
5.2.2 softmax层的作用
  • 使最后一维的向量中的数字缩放到0-1的概率值域内, 并满足他们的和为1.
5.2.3 线性层和softmax层的代码分析
ruby 复制代码 
# 解码器类 Generator 实现思路分析
# init函数 (self, d_model, vocab_size)
    # 定义线性层self.project
# forward函数 (self, x)
    # 数据 F.log_softmax(self.project(x), dim=-1)

class Generator(nn.Module):
    def __init__(self, d_model, vocab_size):
        # 参数d_model 线性层输入特征尺寸大小
        # 参数vocab_size 线层输出尺寸大小
        super(Generator, self).__init__()
        # 定义线性层
        self.project = nn.Linear(d_model, vocab_size)

    def forward(self, x):
        # 数据经过线性层 最后一个维度归一化 log方式
        x = F.log_softmax(self.project(x), dim=-1)
        return x
  • nn.Linear演示:
ini 复制代码 
>>> m = nn.Linear(20, 30)
>>> input = torch.randn(128, 20)
>>> output = m(input)
>>> print(output.size())
torch.Size([128, 30])

6. 完整Transformer模型

将编码器和解码器组合成完整的Transformer模型：

完整的Transformer模型可以表示为：

<math xmlns="http://www.w3.org/1998/Math/MathML"> T r a n s f o r m e r ( X , Y ) = D e c o d e r ( E n c o d e r ( X ) , Y ) \mathrm{Transformer}(X, Y) = \mathrm{Decoder}(\mathrm{Encoder}(X), Y) </math>Transformer(X,Y)=Decoder(Encoder(X),Y)

python 复制代码 
class MyTransform(nn.Module):
    """
    Transformer模型实现
    包含编码器和解码器两部分
    """
    def __init__(self, heads, embed_dim, feed_hidden_size, dropout_p=0.1):
        """
        初始化Transformer模型
        
        Args:
            heads: 注意力头数
            embed_dim: 嵌入维度
            feed_hidden_size: 前馈网络隐藏层大小
            dropout_p: dropout概率
        """
        super().__init__()

        # 创建编码器层模板
        encoder_layer = EncoderLayer(heads=heads, embed_dim=embed_dim,
                                     hidden_size=feed_hidden_size, dropout_p=dropout_p)
        # 创建包含6层的编码器
        self.encoder = Encoder(layer=encoder_layer, N=6, embed_dim=embed_dim)

        # 创建解码器层模板
        decoder_layer = DecoderLayer(heads=heads, embed_dim=embed_dim,
                                     feed_forward_hidden_size=feed_hidden_size, dropout_p=dropout_p)

        # 创建包含6层的解码器
        self.decoder = Decoder(decoder_layer=decoder_layer, n=6, embed_dim=embed_dim)

    def forward(self, x, y, target_mask, source_mask):
        """
        前向传播
        
        Args:
            x: 源序列输入 [batch_size, src_seq_len, embed_dim]
            y: 目标序列输入 [batch_size, tgt_seq_len, embed_dim]
            target_mask: 目标序列掩码（防止未来信息泄露）
            source_mask: 源序列掩码
        
        Returns:
            torch.Tensor: 解码器输出 [batch_size, tgt_seq_len, embed_dim]
        """
        # 编码器处理源序列
        encoder_output = self.encoder(x, source_mask)

        # 解码器处理目标序列，使用编码器输出作为键和值
        decoder_output = self.decoder(y, encoder_output, encoder_output, target_mask)

        return decoder_output

7. 公式与代码实现对照详解

为了更好地理解Transformer中各公式的实现，我们在此详细对照每个重要公式与其对应的代码实现。

7.1 注意力机制公式对照

注意力机制的核心公式：

<math xmlns="http://www.w3.org/1998/Math/MathML"> Attention ( Q , K , V ) = softmax ( Q K T d k ) V \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V </math>Attention(Q,K,V)=softmax(dk QKT)V

对应的代码实现：

python 复制代码 
def attention(q, k, v, mask=None, dropout=None):
    # 获取维度
    embed_dim = k.size(-1)
    
    # 计算 QK^T
    q_k = torch.matmul(q, k.transpose(-1,-2))
    
    # 缩放操作：除以 sqrt(d_k)
    attn_weight = q_k / math.sqrt(embed_dim)
    
    # 应用掩码（如果存在）
    if mask is not None:
        attn_weight = attn_weight.masked_fill(mask == 0, -1e9)
    
    # softmax归一化
    attn_weight = nn.functional.softmax(attn_weight, dim=-1)
    
    # 应用dropout（如果存在）
    if dropout is not None:
        attn_weight = dropout(attn_weight)
    
    # 乘以 V
    res = torch.matmul(attn_weight , v)
    
    return res, attn_weight

7.2 多头注意力公式对照

多头注意力机制的公式：

<math xmlns="http://www.w3.org/1998/Math/MathML"> MultiHead ( Q , K , V ) = Concat ( head 1 , . . . , head h ) W O \text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, ..., \text{head}_h)W^O </math>MultiHead(Q,K,V)=Concat(head1,...,headh)WO

<math xmlns="http://www.w3.org/1998/Math/MathML"> where h e a d i = A t t e n t i o n ( Q W i Q , K W i K , V W i V ) \text{where} \quad \mathrm{head_i} = \mathrm{Attention}(QW_i^Q, KW_i^K, VW_i^V) </math>whereheadi=Attention(QWiQ,KWiK,VWiV)

对应的代码实现（MultiHeadAttention类的forward方法）：

python 复制代码 
def forward(self, q, k, v, mask=None):
    if mask is not None:
        # 扩展mask的维度以匹配多头
        mask = mask.unsqueeze(0)
    
    batch_size = q.size(0)
    heads = self.heads
    embed_dim = q.size(-1)
    d_k = self.d_k
    
    # 对Q、K、V分别应用线性变换，然后reshape为(batch_size, heads, seq_len, d_k)
    q, k, v = [linear(x)
                .view(batch_size, -1, heads, d_k)
                .transpose(1,2)
                for linear,x in zip(self.linears,(q,k,v))]

    # 获取注意力机制输出
    output, attn_weight = attention(q, k, v, mask, self.dropout)
    
    # 合并多头到一个量中
    # 交换维度并合并heads和d_k维度
    res = output.transpose(1,2).contiguous().view(batch_size, -1, embed_dim)
    
    # 最后使用线性层做收尾处理
    return self.linears[-1](res)

7.3 位置编码公式对照

位置编码的公式：

<math xmlns="http://www.w3.org/1998/Math/MathML"> P E ( p o s , 2 i ) = sin ⁡ ( p o s 1000 0 2 i / d model ) PE_{(pos,2i)} = \sin\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right) </math>PE(pos,2i)=sin(100002i/dmodelpos)

<math xmlns="http://www.w3.org/1998/Math/MathML"> P E ( p o s , 2 i + 1 ) = cos ⁡ ( p o s 1000 0 2 i / d model ) PE_{(pos,2i+1)} = \cos\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right) </math>PE(pos,2i+1)=cos(100002i/dmodelpos)

对应的代码实现（PositionalEmbedding类的__init__方法）：

python 复制代码 
def __init__(self, max_length, embed_dim, dropout_p=0.1):
    super().__init__()
    self.max_length = max_length
    self.embed_dim = embed_dim

    # Dropout层用于防止过拟合
    self.dropout = nn.Dropout(p=dropout_p)

    # 创建位置编码矩阵 [max_length, embed_dim]
    pe = torch.zeros(max_length, embed_dim)
    
    # 生成位置信息 [max_length, 1]
    pos = torch.arange(0, max_length).unsqueeze(1)
    
    # 生成维度索引 0, 2, 4, ..., embed_dim-2 （只取偶数索引）
    tow_i = torch.arange(0, embed_dim, 2)
    
    # 计算角度频率参数
    tmp_v = torch.exp((math.log(10000) * -tow_i / self.embed_dim))

    # 计算角度值：pos * 角度频率
    fn_v = tmp_v * pos

    # 偶数位置使用sin编码
    pe[:, 0::2] = torch.sin(fn_v)
    # 奇数位置使用cos编码
    pe[:, 1::2] = torch.cos(fn_v)

    # 增加batch维度 [1, max_length, embed_dim]
    pe = pe.unsqueeze(0)

    # 注册为buffer，不会被更新，但会随模型保存和加载
    self.register_buffer('pe', pe)

7.4 层归一化公式对照

层归一化的公式：

<math xmlns="http://www.w3.org/1998/Math/MathML"> μ = 1 H ∑ i = 1 H x i \mu = \frac{1}{H}\sum_{i=1}^{H} x_i </math>μ=H1∑i=1Hxi

<math xmlns="http://www.w3.org/1998/Math/MathML"> σ 2 = 1 H ∑ i = 1 H ( x i − μ ) 2 \sigma^2 = \frac{1}{H}\sum_{i=1}^{H} (x_i - \mu)^2 </math>σ2=H1∑i=1H(xi−μ)2

<math xmlns="http://www.w3.org/1998/Math/MathML"> y = x − μ σ 2 + ϵ ⊙ γ + β y = \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}} \odot \gamma + \beta </math>y=σ2+ϵ x−μ⊙γ+β

对应的代码实现（LayerNorm类的forward方法）：

python 复制代码 
def forward(self, x):
    # 计算平均数
    x_mean = torch.mean(x, keepdim=True, dim=-1)
    
    # 计算标准差
    x_std = torch.std(x, keepdim=True, dim=-1)
    
    # 计算 (x-平均数) / (标准差+eps) = 标准化后的x
    res = (x - x_mean) / (x_std + self.eps)
    
    # 返回 W * x + b，应用可学习的缩放和偏移
    return self.w * res + self.b

7.5 前馈网络公式对照

前馈网络的公式：

<math xmlns="http://www.w3.org/1998/Math/MathML"> F F N ( x ) = max ⁡ ( 0 , x W 1 + b 1 ) W 2 + b 2 \mathrm{FFN}(x) = \max(0, xW_1 + b_1)W_2 + b_2 </math>FFN(x)=max(0,xW1+b1)W2+b2

对应的代码实现（FeedForward类的forward方法）：

python 复制代码 
def forward(self, x):
    # 第一层线性变换: xW_1 + b_1
    x = self.linear1(x)

    # ReLU激活: max(0, xW_1 + b_1)
    x = self.relu(x)

    # Dropout防止过拟合
    x = self.dropout(x)

    # 第二层线性变换: max(0, xW_1 + b_1)W_2 + b_2
    x = self.linear2(x)

    return x

7.6 子层连接公式对照

子层连接的公式：

<math xmlns="http://www.w3.org/1998/Math/MathML"> S u b l a y e r C o n n e c t i o n ( x , S u b l a y e r ) = L a y e r N o r m ( x + D r o p o u t ( S u b l a y e r ( x ) ) ) \mathrm{SublayerConnection}(x, \mathrm{Sublayer}) = \mathrm{LayerNorm}(x + \mathrm{Dropout}(\mathrm{Sublayer}(x))) </math>SublayerConnection(x,Sublayer)=LayerNorm(x+Dropout(Sublayer(x)))

对应的代码实现（SubLayers类的forward方法）：

python 复制代码 
def forward(self, x, layer_fn):
    # 对输入应用指定的层函数，然后进行层归一化和dropout
    # 最后与原始输入进行残差连接（x + res）
    res  = self.dropout(self.norm(layer_fn(x)))
    return x + res

7.7 编码器层公式对照

编码器层的公式：

<math xmlns="http://www.w3.org/1998/Math/MathML"> E n c o d e r L a y e r ( x ) = S u b l a y e r C o n n e c t i o n ( S u b l a y e r C o n n e c t i o n ( x , S e l f A t t e n t i o n ) , F F N ) \mathrm{EncoderLayer}(x) = \mathrm{SublayerConnection}(\mathrm{SublayerConnection}(x, \mathrm{SelfAttention}), \mathrm{FFN}) </math>EncoderLayer(x)=SublayerConnection(SublayerConnection(x,SelfAttention),FFN)

对应的代码实现（EncoderLayer类的forward方法）：

python 复制代码 
def forward(self, x, mask=None):
    # 第一层：自注意力机制
    x = self.layers[0](x, lambda x: self.multi_head_attn(x, x, x, mask))

    # 第二层：前馈神经网络
    x = self.layers[1](x, self.feed_ward)
    
    return x

7.8 解码器层公式对照

解码器层的公式：

<math xmlns="http://www.w3.org/1998/Math/MathML"> D e c o d e r L a y e r ( x , e n c o u t ) = S u b l a y e r C o n n e c t i o n ( S u b l a y e r C o n n e c t i o n ( S u b l a y e r C o n n e c t i o n ( x , M a s k e d S e l f A t t e n t i o n ) , E n c o d e r A t t e n t i o n ) , F F N ) \mathrm{DecoderLayer}(x, enc_out) = \mathrm{SublayerConnection}(\mathrm{SublayerConnection}(\mathrm{SublayerConnection}(x, \mathrm{MaskedSelfAttention}), \mathrm{EncoderAttention}), \mathrm{FFN}) </math>DecoderLayer(x,encout)=SublayerConnection(SublayerConnection(SublayerConnection(x,MaskedSelfAttention),EncoderAttention),FFN)

对应的代码实现（DecoderLayer类的forward方法）：

python 复制代码 
def forward(self, q, k, v, target_mask=None, source_mask=None):
    # 第一层：目标序列的自注意力（使用target_mask防止看到未来信息）
    res_1 = self.layers[0](q, lambda x: self.multi_head_attn(x, x, x, target_mask))

    # 第二层：编码器-解码器注意力（查询来自前一层，键值来自编码器输出）
    res_2 = self.layers[1](res_1, lambda x: self.multi_head_attn(x, k, v, source_mask))

    # 第三层：前馈神经网络
    res_3 = self.layers[2](res_2, self.feed_forward)

    return res_3

7.9 完整Transformer模型公式对照

完整Transformer模型的公式：

<math xmlns="http://www.w3.org/1998/Math/MathML"> T r a n s f o r m e r ( X , Y ) = D e c o d e r ( E n c o d e r ( X ) , Y ) \mathrm{Transformer}(X, Y) = \mathrm{Decoder}(\mathrm{Encoder}(X), Y) </math>Transformer(X,Y)=Decoder(Encoder(X),Y)

对应的代码实现（MyTransform类的forward方法）：

python 复制代码 
def forward(self, x, y, target_mask, source_mask):
    # 编码器处理源序列
    encoder_output = self.encoder(x, source_mask)

    # 解码器处理目标序列，使用编码器输出作为键和值
    decoder_output = self.decoder(y, encoder_output, encoder_output, target_mask)

    return decoder_output

8. 辅助函数

一些辅助函数帮助构建模型：

python 复制代码 
def clone_modules(module, N):
    """
    克隆N个相同的模块
    
    Args:
        module: 要克隆的模块
        N: 克隆的数量
    
    Returns:
        nn.ModuleList: 包含N个相同模块的列表
    """
    return nn.ModuleList(copy.deepcopy(module) for _ in range(N))

def get_mask(size):
    """
    生成上三角掩码矩阵，用于防止未来信息泄露（在解码器中使用）
    
    Args:
        size: 掩码矩阵的尺寸 (heads, seq_len, seq_len)
    
    Returns:
        torch.Tensor: 上三角为0，下三角和对角线为1的掩码矩阵
    """
    tensor = torch.ones(size=size, dtype=torch.long)
    # triu生成上三角矩阵，k=1表示对角线上方的元素为1，其余为0
    # 1-操作将其反转，使对角线和下三角为1，上三角为0
    return 1-torch.triu(tensor, 1)

9. 测试代码

测试模型各部分功能：

python 复制代码 
def test_transform():
    """
    测试完整的Transformer模型
    """
    # 占位符，无实际作用
    pass

    # 创建测试源序列数据
    x = torch.tensor([
        [1, 2, 3, 4],
        [2, 4, 5, 6]
    ])
    embed_dim = 512
    # 创建嵌入序列模块
    embedding = EmbeddingSequential(1000, 512, 60)
    # 获取源序列嵌入表示
    embedding_x = embedding(x)
    print('EmbeddingSequential', embedding_x.shape)
    heads = 8
    # 生成源序列掩码
    source_mask = get_mask(size=(heads, x.size(-1), x.size(-1)))
    dropout_p = 0.1
    hidden_size = 2048

    # 创建目标序列数据
    y = torch.tensor([
        [1, 2, 3, 4, 5, 6],
        [2, 3, 4, 5, 6, 7]
    ])

    # 深拷贝嵌入模块处理目标序列
    embed_y = copy.deepcopy(embedding)(y)

    print('embed_y', embed_y)
    # 生成目标序列掩码
    target_mask = get_mask(size=(heads, y.size(-1), y.size(-1)))
    # 创建Transformer模型
    transformer = MyTransform(heads=heads, embed_dim=embed_dim, feed_hidden_size=hidden_size, dropout_p=dropout_p)

    # Transformer前向传播
    decoder_output = transformer(embedding_x, embed_y, target_mask, source_mask)

    # 创建生成器
    generator = Generator(embed_dim, output_size=2000)

    # 生成预测结果
    pre_v = generator(decoder_output)

    print('pre_v', pre_v)

10. 项目源码

本项目完整源码已开源，您可以在以下GitHub仓库中获取：

github.com/KobeCYL/tra...

源码包含了完整的Transformer实现，以及详细的中文注释，方便学习和理解。项目结构如下：

bash 复制代码 
transformer-implementation/
├── common.py              # 公共组件：注意力机制、多头注意力、层归一化等
├── encoder_module.py      # 编码器模块实现
├── decoder_module.py      # 解码器模块实现
├── embeddings.py          # 词嵌入和位置编码实现
├── generator.py           # 输出生成器
├── transform.py           # Transformer模型主体
└── test.py               # 测试代码

您可以通过以下方式使用该项目：

bash 复制代码 
git clone https://github.com/KobeCYL/transformer-implementation.git
cd transformer-implementation
python test.py

欢迎提交Issue和Pull Request，共同完善这个教学用途的Transformer实现。

11. 总结

通过手写Transformer的实现，我们可以更深入地理解其内部工作机制：

  1. 注意力机制：核心组件，允许模型关注输入序列的不同部分
  2. 多头注意力：并行计算多个注意力表示，增强模型的表达能力
  3. 位置编码：为模型提供序列顺序信息
  4. 残差连接和层归一化：稳定训练过程，加速收敛
  5. 前馈网络：对每个位置的表示进行非线性变换

Transformer的这些设计使其能够并行处理序列数据，有效捕获长距离依赖关系，成为现代NLP模型的基础架构。通过手动实现这些组件，我们不仅加深了对Transformer架构的理解，也为后续的模型改进和优化奠定了基础。

12. 关注我们

如果你觉得这篇文章对你有帮助，欢迎：

  • 点赞支持：如果内容对你有帮助，请不要吝啬你的赞👍
  • 分享传播：将文章分享给更多需要的朋友，让知识传递更远
  • 关注作者：关注我的GitHub和博客，获取更多深度学习和自然语言处理的干货内容
  • 评论交流：在评论区留下你的想法和问题，我们一起讨论学习

更多关于Transformer、BERT、GPT等前沿NLP技术的深度解析，敬请关注！

让我们一起在AI的道路上不断前行，探索更多技术的奥秘！🚀

相关推荐
AI人工智能+2 小时前
表格识别技术，通过目标检测、结构分析和文字识别三步骤，实现对纸质档案表格的智能解析
nlp·ocr·表格识别
AI人工智能+2 天前
告别手动录入：文档抽取技术如何让RPA处理非结构化数据？
nlp·ocr·rpa·文档抽取
AI人工智能+3 天前
文档抽取技术：通过OCR、关键信息抽取和数据标准化三大环节，实现了对银行流水的高效解析
nlp·ocr·文档抽取
0小豆03 天前
【系列开篇】从零构建智能字幕校准系统：一个AI+微服务的完整实战之旅
spring boot·python·nlp·微服务架构·实战项目·spacy·ai算法
大千AI助手8 天前
BPE（Byte Pair Encoding）详解：从基础原理到现代NLP应用
人工智能·自然语言处理·nlp·分词·bpe·大千ai助手·字节对编码
故事挺秃然9 天前
大型语言模型（LLM）架构大比拼
语言模型·nlp
苦瓜汤补钙9 天前
论文阅读——Segment Anything（Meta AI）——SAM
论文阅读·图像处理·人工智能·nlp·ai编程
合作小小程序员小小店9 天前
舆情，情感微博系统demo，基于python+qt+nlp,开发语言python,界面库qt，无数据库版，数据来自第三方网站获取，
开发语言·pytorch·qt·自然语言处理·nlp
故事挺秃然10 天前
NLP模型优化
人工智能·自然语言处理·nlp
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03BongoCat - 跨平台键盘猫动画工具04综合整理：pdf预览显示：你尝试预览的文件可能对你的计算机有害。如果你信任此文件以及其来源，请打开此文件以看其内容，如何解决以正常预览文件05Linux下V2Ray安装配置指南06安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）07jdk21下载、安装（Windows、Linux、macOS）08《大数据技术原理与应用》实验报告三 熟悉HBase常用操作09Labelme从安装到标注：零基础完整指南10PyCharm 社区版全平台安装指南