总观
数据结构就是组织数据以及存储数据的一种方式,不同的数据结构在不同的场景之下会有不同的作用。而算法就是将输入的数据经过一系列的计算步骤,最后输出我们想要的结果。
为了更好的说明算法复杂度的问题,首先来看一道算法题:
https://leetcode.cn/problems/rotate-array
解法一:暴力解法
题干给了我们一个数组,要轮转k次,显然需要用到循环,那我们只需要先考虑轮转一次的方法,剩下k次只需要利用循环就可以了。
因此就产生了我们的暴力解法,以题干示例数组 **nums = **[1,2,3,4,5,6,7]****为例。
我们要先将轮转的那个元素保存在变量tmp里边,也就是7,再定义一个变量i指向数组元素6下标的位置,开始循环,我们将nums[i]给给nums[i+1],然后i--,一直循环直到i==0的时候,此时将下标0的数据给给完下标为1之后i--,循环结束,最后将tmp赋值给nums[i+1]就完成了依次轮转操作。
代码实现:
cpp
void rotate(int* nums, int numsSize, int k) {
while(k--)
{
int tmp = nums[numsSize - 1];
for(int i = numsSize - 1 - 1;i >= 0;i--)
{
nums[i + 1] = nums[i];
}
nums[0] = tmp;
}
}复杂度的概念
对于上边的那道算法题,用解法一去提交的话会超出时间限制,这里所谓的时间限制就涉及到了复杂度的概念,复杂度分为时间复杂度和空间复杂度,它们用于衡量一个算法的好坏,时间复杂度就是用于衡量一个算法的运行快慢,空间复杂度就是用于衡量一个算法运行所需要的额外空间。当然由于时代的发展,现代的计算机的容量一般都是足够的,所以空间复杂度相比于时间复杂度来说就显得少重要一点。
时间复杂度
时间复杂度是一个函数表达式,它不是去计算程序所执行的具体的时间,因为相同的代码可能在不用的编译器上的运行时间都会有着区别,这就带来了不确定性。但是一段相同的代码它所执行的次数肯定是确定的,这里所说的执行的次数其实就比如像这个算法里边的for循环执行了多少次这样的一个概念。最后总结一下,时间复杂度就可以等同理解为程序的执行次数。
一段C语言的代码,它最终会被编译器编译成一段二进制的指令,所以程序的运行时间就等于二进制指令运行时间乘执行次数。其中每一条的二进制指令的执行时间是可以忽略不计的,因为CPU每一秒可能就可以执行成千上万条指令,因此程序的运行时间也可以等价理解为程序的执行次数。
所以通过分析时间复杂度,我们就可以知道不同程序的快与慢。
时间复杂度的经典案例分析
案例一:计算Func1函数的时间复杂度
cpp
void Func1(int N)
{
int count = 0;
for (int i = 0; i < N; ++i)
{
for (int j = 0; j < N; ++j)
{
++count;
}
}
for (int k = 0; k < 2 * N; ++k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
}通过分析很快就可以得出程序的执行次数 T(N) = N * N + 2 * N + 10 ,但是我们描述时间复杂度的时候并不会这样去描述,随着N的增大,N * N 的增长速度是远远超过其他剩下的部分的,因此除去 N * N 的部分其实是可以忽略不计的,通过N * N 就可以去描述案例一的时间复杂度。表示为O(N^2)。这就是大O表示法。
大O渐近表示法:用来描述时间复杂度(本质是一个趋势,但在计算的时候理解为执行次数就可以了。)
注意:下边函数T里边所有的N其实都是指代变量,没有具体的含义。
我们一般是用大O表示法去描述算法的时间复杂度。它有三个规则。
时间复杂度函数式T(N)中,只保留最⾼阶项,去掉那些低阶项,因为当N不断变大时,低阶项对结果影响越来越⼩,当N⽆穷⼤时,就可以忽略不计了。
如果最⾼阶项存在且不是1,则去除这个项⽬的常数系数,因为当N不断变⼤,这个系数对结果影响越来越⼩,当N⽆穷⼤时,就可以忽略不计了。
T(N)中如果没有N相关的项⽬,只有常数项,⽤常数1取代所有加法常数。
案例二:
cpp
void Func2(int N)
{
int count = 0;
for (int k = 0; k < 2 * N; ++k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
printf("%d\n", count);
}先写出执行次数函数T的表达式,T(N) = 2 * N + 10 ,根据大O表示法的规则可以轻松得出时间复杂度为O(N)。
案例三:
cpp
void Func3(int N, int M)
{
int count = 0;
for (int k = 0; k < M; ++k)
{
++count;
}
for (int k = 0; k < N; ++k)
{
++count;
}
printf("%d\n", count);
}T(N、M) = M + N,时间复杂度O(M + N)。
其实还可以做进一步的讨论,讨论M和N的范围
如果M == N O(N) / O(M)
如果M >> N O(M)
如果M << N O(N)
案例四:
cpp
void Func4(int N)
{
int count = 0;
for (int k = 0; k < 100; ++k)
{
++count;
}
printf("%d\n", count);
}T(N) = 100,O(1)。
案例五:
cpp
const char* strchr(const char* str, char character)
{
const char* p_begin = s;
while (*p_begin != character)
{
if(*p_begin == '\0')
return NULL;
p_begin++;
}
return p_begin;
}本题的代码整体逻辑就是指定了一个字符character,p_begin一开始指向str字符串的第一个字符的位置,便利str字符串寻找,找到了返回地址,找不到返回NULL。
有了上边对于案例五代码的逻辑分析,我们就知道它的时间复杂度受到character,假设这个字符串为 "Hello................World\0",总长度为n。如果要查找的字符正好是H,只需要执行一次,时间复杂度就为O(1),如果要查找的字符为d,需执行n次,时间复杂度就变成了O(N),那如果要查找的字符正好在字符串中间的位置,T(N) == N / 2,时间复杂度为O(N)。
以上的三种情况就对应了最好情况,平均情况和最差情况。而大O表示法一般只会关心最差的情况。
案例六:
cpp
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if(exchange == 0)
break;
}
}上边是冒泡排序的代码,是一个循环嵌套,这里循环嵌套的外循环是影响内循环的,我们可以列一个表格。
外循环 内循环
第一次 n - 1
第二次 n - 2
第三次 n - 3
.
.
.
第n次 1
最终执行次数为T(N) = 1 + 2 + 3 + ... + (n - 1)
通过等差数列求和公式化简得:T(N) = (N^2 - N) / 2
由大O表示法的规则得出时间复杂度为O(N^2)。
案例七:
cpp
void func5(int n)
{
int cnt = 1;
while (cnt < n)
{
cnt *= 2;
}
}像这种循环次数受到变量控制的代码,直接假设总的执行次数为k,每次进入while循环,cnt都乘2,执行k次跳出循环的话就说明满足了 2^k == n 这个式子,最终算出来 k = logn,则最终的时间复杂度为O(logn)。注意这里有一个小细节,时间复杂度如果是log函数,那它的底数就可以直接省略掉了,因为当n趋于无穷大的时候,log函数为无穷大了,底数是几都不重要了。按照这个道理,用lgn表示也跟logn是一个意思。它们在时间复杂度里边是等价的。
案例八:
cpp
long long Fac(size_t N)
{
if (0 == N)
return 1;
return Fac(N - 1) * N;
}这是一段递归代码,求n!,那递归算法的时间复杂度 = 单次递归的时间复杂度 * 递归次数。
这个案例里边单次递归次数为1,而递归次数为n + 1次,从Fac(N) -> Fac(N - 1) -> Fac(N - 2) -> ......Fac(0)。总N + 1次。最终的总的执行次数就为(N + 1) * 1,时间复杂度就为O(N)。
空间复杂度
跟时间复杂度一样,空间复杂度也是用大O表示法去表示,它也是一个表达式,它计算的是函数体内因执行算法所额外开辟的空间。像形参以及函数栈帧之类的都不用管了,因为它们在编译的时候就已经确定好空间了。说白了空间复杂度就是申请空间的次数,不用管具体是多少个字节。
案例一:
cpp
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i-1] > a[i])
{
Swap(&a[i-1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}案例一里的函数体内就创建了exchange,end等变量,空间复杂度就为O(1)。
案例二:
cpp
long long Fac(size_t N)
{
if(N == 0)
return 1;
return Fac(N-1)*N;
}递归算法的空间复杂度 = 单次递归的空间复杂度 * 递归次数,上述代码的递归次数已经在上边分析过了,为n + 1次,而单次递归的空间复杂度为O(1),所以最终的空间复杂度为O(N)。
常见复杂度对比
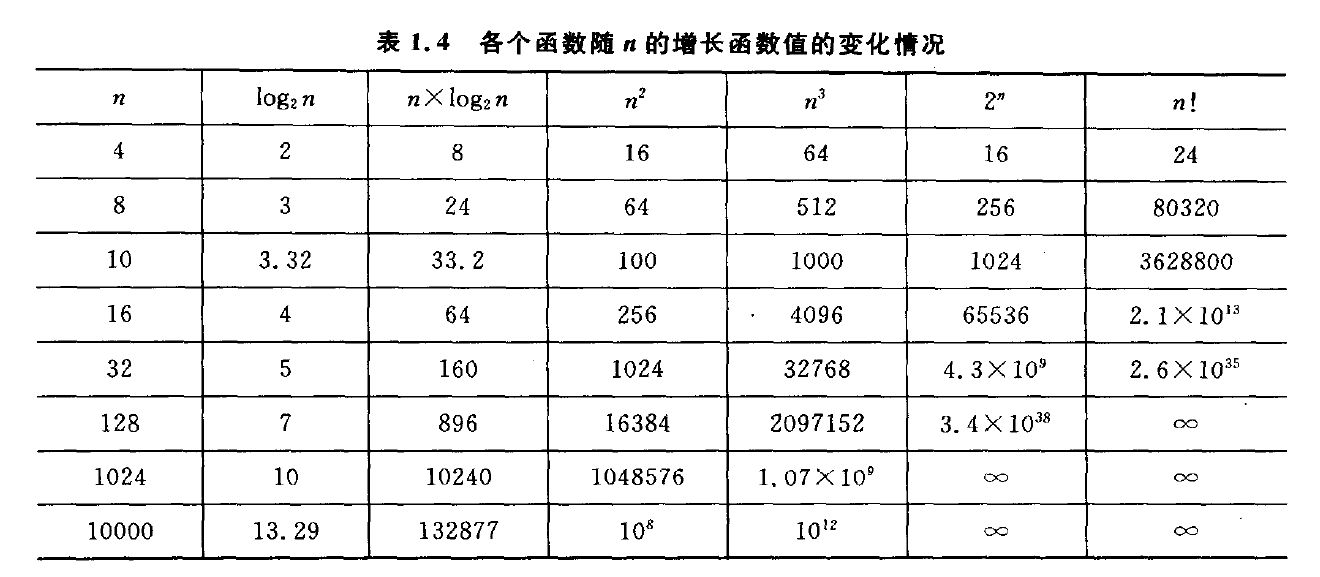
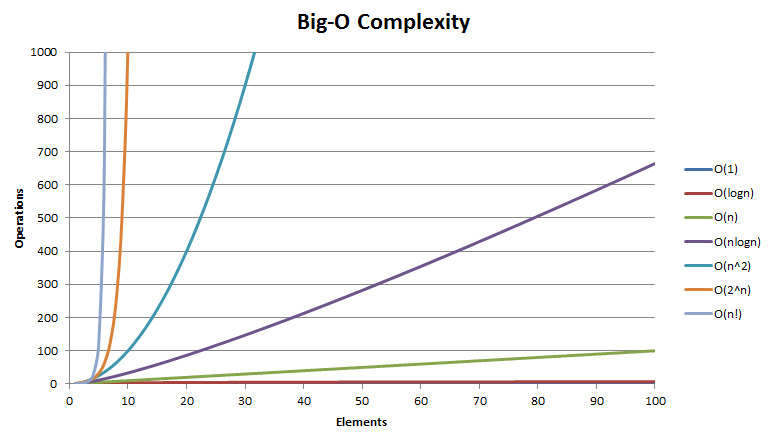
由上边两张表可以看出不用的时间复杂度之间的时间差异。
再看轮转数组
在总观那个大标题里边已经给出了解法一,暴力解法,简单分析一下就可得出它的时间复杂度为O(N^2) (经过分析很容易可以知道执行次数为k * numsSize,为两个变量,我们可以将它们都看成N,因为numsSize和k谁大谁小不知道,都有可能为无穷大,所以我们可以将它们看成统一的变量N),空间复杂度为O(1)。
解法二:创建一个新数组
创建一个跟题给数组nums一样大小的数组tmp,将nums数组里边要轮转的后k个数据放到tmp的前k个位置,nums数组里剩下的数据依次放到tmp里边就可以了。这样一来我们只需要从头便利nums数组一次。
题给示例:
轮转次数k == 3
nums 1,2,3,4,5,6,7
tmp 5,6,7,1,2,3,4
下标 0,1,2,3,4,5,6
先定义一个变量i指向nums数组下标为0的位置,nums[i]给给tmp[i+ k],接着i++,但是当i的值为4的时候i + k == 7就已经越界了,此时我们只需要将(i + k) % numsSize,此时的i + k就相当于变成了0,而i为4,即指向了要轮转的数字,直到i越界,整个轮转数组的结果就到了tmp数组里边,最后将tmp数组里边的值赋值到nums数组就可以了。
代码实现:
cpp
void rotate(int* nums, int numsSize, int k) {
//创建新数组
int tmp[numsSize];
//向右轮转k次
for(int i = 0;i < numsSize;i++)
{
int j = (i + k) % numsSize;
tmp[j] = nums[i];
}
//拷贝
for(int i = 0;i < numsSize;i++)
{
nums[i] = tmp[i];
}
}易得时间复杂度为O(N),空间复杂度为O(N),这就是典型的空间换时间操作。
解法三:逆置
先将前numsSize - k个数据逆置,再将后k个数据逆置,最后将数组整体逆置,就得到了我们想要的最终数组。时间复杂度为O(N),空间复杂度为O(1)。
我们只需要写一个逆置reverese函数,它的两个形参就代表要逆置区间的左右下标,但是我们要考虑到边界情况,轮转次数k可能大于数组的长度,这就导致数组发生越界情况,我们只需要将轮转次数k % numsSize就可以避免这种情况了。
关于时间复杂度还想解释一下,reverse函数里边left和right合力便利了数组一遍,单独看一个变量的话其实最差的情况就便利了N / 2个数组,因为一个while循环里边,left和right同时在移动,那根据大O表示法,时间复杂度就为O(N)。
代码实现
cpp
void reverse(int* num,int left,int right)
{
while(left < right)
{
int tmp = num[left];
num[left] = num[right];
num[right] = tmp;
left++;
right--;
}
}
void rotate(int* nums, int numsSize, int k) {
k = k % numsSize;
reverse(nums,0,numsSize - k - 1);
reverse(nums,numsSize - k,numsSize - 1);
reverse(nums,0,numsSize - 1);
}