NLP基础(八)_马尔可夫模型

马尔可夫模型（Markov Model ）是一种数学模型，用于描述一个系统在某个时间点的状态 如何随着时间转移到另一个状态，并假设未来的状态仅依赖于当前状态，而与过去状态无关 ，这就是著名的 马尔可夫性（Markov property）。

4.0 马尔可夫与贝叶斯关系

马尔可夫模型专注于状态如何随时间变化；贝叶斯方法则专注于如何根据观察数据推断未知量。在实际建模中，常常将马尔可夫模型结构 + 贝叶斯推理方法结合使用，比如隐马尔可夫模型、动态贝叶斯网络（DBN）。

（1）核心关系

马尔可夫模型可以看作是贝叶斯思想的一种特例或具体应用，尤其是在时间序列建模中。

它使用了条件概率 ------ 这正是贝叶斯方法的核心。

**条件概率：**告诉你："在某事已知的前提下，其他事情有多可能"

贝叶斯推理：用条件概率 + 观察数据，不断修正我们对未知的估计

（2）相同点

方面	描述
基于概率	两者都依赖概率建模，核心都是不确定性建模
用到条件概率	都涉及 **P(A
可用于推理与预测	两者都可用于做状态推理或未来预测
可用于图模型表示	都可以使用概率图模型（如贝叶斯网络）表示变量之间的关系

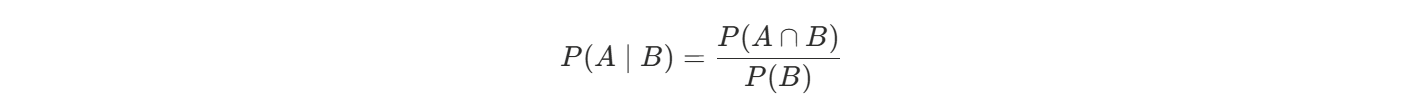
P(A∩B)：A 和 B 同时发生的概率
P(B)：条件（B 发生）的概率
P(A|B)：在 B 发生的前提下 A 发生的概率

（3）不同点

维度	马尔可夫模型	贝叶斯方法
关注点	序列中的状态转移过程	给定观测后对未知变量的后验估计
是否时间依赖	是，模型强调时间序列上的状态转移	不一定有时间顺序
是否马尔可夫性假设	有，当前状态仅依赖前一状态	没有此假设，可依赖任意变量
常用形式	马尔可夫链、HMM、MDP	贝叶斯分类器、贝叶斯网络、贝叶斯推断
参数学习方式	可用最大似然或 EM 算法	常用贝叶斯推断（如贝叶斯公式）

（4）结合的例子：隐马尔可夫模型（HMM）就是两者的结合体

HMM 本质上是一个马尔可夫链，但状态是隐藏的；
我们通过贝叶斯公式来推断当前最可能的隐藏状态；
常见任务如：已知观测序列 O1,O2,...,Ot推断状态序列 S1,S2,...,St

HMM 的推理过程使用了：

条件概率
贝叶斯推理
马尔可夫性假设（状态转移只依赖于上一个状态）

4.1 基本定义

马尔可夫模型是一种随机过程，具有以下特性：

马尔可夫性：

对于任意状态序列 S1,S2,...,Sn，满足：

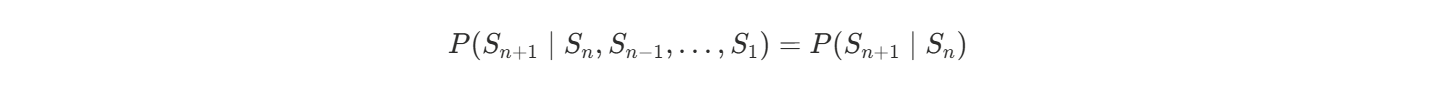
也就是说，下一步的状态只和当前状态有关，而与之前的历史无关。

4.2 常见的马尔可夫模型

模型	全称	简要描述
马尔可夫链（Markov Chain）	无观察、只有状态转移的模型	比如天气：今天晴 → 明天阴
隐马尔可夫模型（Hidden Markov Model, HMM）	状态不可见，观察值可见	比如情感识别：真实情绪隐藏，通过语音观察
马尔可夫决策过程（Markov Decision Process, MDP）	在马尔可夫链基础上加入行动与奖励，用于决策	应用于强化学习
高阶马尔可夫模型	状态依赖于多个前序状态	比如二阶模型依赖前两个状态

4.3 马尔可夫链示意

（最简单的马尔可夫模型）

假设天气状态只有：☀️晴天（sunny）和 🌧️雨天（rainy）

当前天气	明天是晴天的概率	明天是雨天的概率
☀️ 晴天	0.8	0.2
🌧️ 雨天	0.4	0.6

这个系统就可以用转移矩阵来描述：

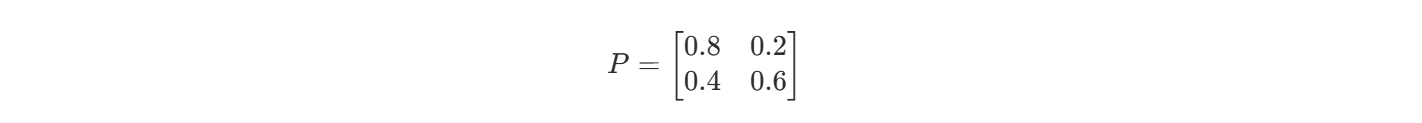
4.4 应用场景

自然语言处理：比如词性标注、分词（HMM）
语音识别：声音对应的发音状态建模（HMM）
金融建模：股价状态转移建模
用户行为预测：比如网站点击行为
天气预测：气象状态的转移模型

4.5 隐马尔可夫模型

假设你是一个侦探，只能听到某人每天的活动（吃饭、睡觉、打游戏），但看不到他的真实心情（高兴/抑郁）。心情是"隐藏状态"，活动是"可观察值"。

你要根据这些可观察行为，反推出背后的心理状态序列 ，这就是典型的隐马尔可夫模型（HMM）。

4.5.1 Viterbi(维特比)算法

Viterbi（维特比）算法是隐马尔可夫模型（HMM）中最核心的解码算法，它的作用是：

在给定观测序列的前提下，找出最可能的隐藏状态序列。

这正好契合中文分词、语音识别、词性标注等任务的需求。

1. 什么是 Viterbi 算法？

Viterbi 算法是一种动态规划算法，用于在 HMM 中求解：

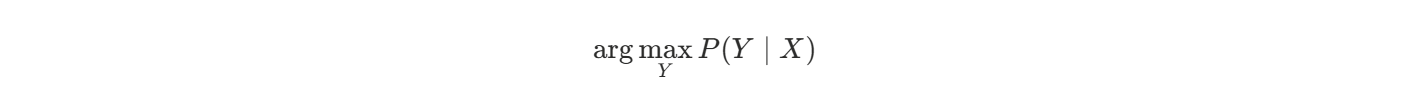
即：已知观测序列 X=x1,x2,...,xT，

求出最可能的状态序列 Y=y1,y2,...,yT。

它不是穷举所有路径（那样是指数复杂度），而是通过分阶段找最大概率路径，效率是线性的。

2. 为什么需要 Viterbi？

因为在 HMM 中，我们观测到的只是字/声音/图像等输入，

但我们真正想知道的是其隐藏的状态，比如：

应用场景	观测值（X）	隐状态（Y）
中文分词	汉字序列	每字是词的 B/M/E/S 标签
语音识别	声波信号	文字或音素
词性标注	单词序列	每个单词的词性（名词、动词等）

这些"状态"无法直接观察，需要通过 Viterbi 计算它们的最可能序列。

3. Viterbi 核心公式

Viterbi 使用以下动态规划递推公式：

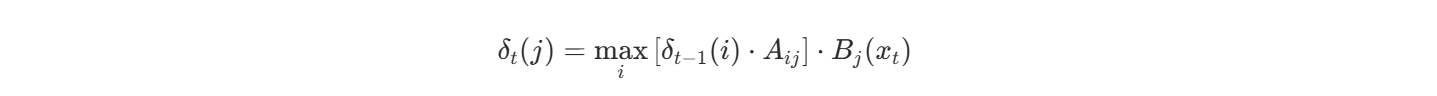
它表示在第 t 时刻状态 j 的最大概率路径：

δt−1(i)：前一时刻状态 iii 的最大概率
Aij：从状态 iii 转移到 jjj 的概率
Bj(xt)：在状态 j 生成观测 xt 的概

它逐步记录最优路径，最终反向回溯得到完整的状态序列。

4. 特点与优势

优点	描述
高效	时间复杂度为 O(N²T)，远小于穷举所有路径（指数级）
精准	能输出整个最优路径，而不仅是每一步的最优状态
可扩展	可用于标准 HMM、条件随机场（CRF）等序列模型

4.5.2 HMM 分词步骤

HMM（隐马尔可夫模型）分词 是一种基于统计模型的中文分词方法，它将分词问题建模为状态序列预测问题 。下面是 HMM 中文分词的完整步骤，包括原理和实际流程：

（1）基本原理

将分词问题转化为 标注问题：

每个汉字被标注为对应的词位状态：

标签	含义
B	一个词的开头（Begin）
M	一个词的中间（Middle）
E	一个词的结尾（End）
S	单字词（Single）

例如："中国人" → 标注为：中/B 国/E 人/S

（2）HMM分词5个步骤

1️⃣ 训练阶段（离线）

训练数据：大量人工分词后的语料，获得以下三类概率参数：

参数	含义	作用
初始概率	每个状态作为句子起始的概率 P(y1)	预测句首的词位标签
状态转移概率 A	当前状态转移到下一状态的概率 P(yt+1	yt)
发射概率 B	在某个状态下生成某字的概率 P(xt	yt)

2️⃣ 构造状态集合

定义状态集合：S = {B, M, E, S}

这4个状态是 HMM 的隐状态集合。

3️⃣ 输入句子作为观测序列

比如：观音山大悲殿

这个序列中的每个字就是观测值 x1,x2,...,xn

4️⃣ 使用 Viterbi 算法 进行最优状态路径推断

输入：观测序列（每个汉字）

输出：最可能的状态序列（标签序列 B/M/E/S）

Viterbi 算法是动态规划，逐字寻找最大概率路径：

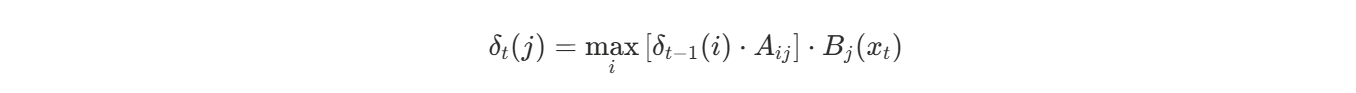
它表示在第 t 时刻状态 j 的最大概率路径：

δt−1(i)：前一时刻状态 i 的最大概率
Aij：从状态 i 转移到 j 的概率
Bj(xt)：在状态 j 生成观测 xt 的概

5️⃣ 根据预测标签切分词语

预测结果：

复制代码

观/B 音/M 山/E 大/B 悲/M 殿/E

切分结果：

复制代码

观音山 / 大悲殿

（3）总结

复制代码

输入句子 → 将每个字作为观测值 →
使用 HMM 模型（初始 + 转移 + 发射概率） →
通过 Viterbi 算法预测最可能的状态序列 →
根据状态标签分词

应用与工具

很多中文 NLP 库使用 HMM 分词，如：

jieba：支持 HMM 模式（默认用于新词发现）
THULAC 、HanLP：也支持 HMM 分词或其改进版本

4.5.3 HMM 中文分词示例

下面通过一个完整、简单、注释清晰的 HMM 中文分词示例，包括：

✅ 语料标注（手动语料）
✅ 统计三类 HMM 概率（初始、转移、发射）
✅ 使用 Viterbi 算法预测最优标签序列
✅ 还原为分词结果

（1）示例语料（已分词）

用极简语料，分好词如下：

复制代码

观音山 大悲殿 我 爱 北京

（2）完整 Python 示例代码（带注释）

复制代码

from collections import defaultdict, Counter

# 1️⃣ 步骤一：准备训练语料并打标签（BMES）
def word_to_tags(word):
		# 如果是 单字词（如"我"），就直接标记为 S。
    if len(word) == 1:
        return [(word, 'S')]
    # 如果是 两个字的词（如"北京"），第一个是 B，第二个是 E。
    elif len(word) == 2:
        return [(word[0], 'B'), (word[1], 'E')]
    else:
        tags = [('B', word[0])]                # 第一个字标 B
        tags += [('M', c) for c in word[1:-1]] # 中间所有字标 M
        tags.append(('E', word[-1]))           # 最后一个字标 E
        return [(c, t) for t, c in tags]

# 示例训练语料（每句是一个词列表）
sentences = [
    ['观音山', '大悲殿'],
    ['我', '爱', '北京']
]

# 转换为 [(字, 标签)] 格式
tagged_data = []
'''
最终 tagged_data 是一个二维列表，每一项是一个句子的字级别标注序列
[
    [('观','B'), ('音','M'), ('山','E'), ('大','B'), ('悲','M'), ('殿','E')],
    [('我','S'), ('爱','S'), ('北','B'), ('京','E')]
]
'''
for sentence in sentences:
    tagged_sentence = []
    for word in sentence:
        tagged_sentence.extend(word_to_tags(word))
    tagged_data.append(tagged_sentence)

方法	作用
`append(x)`	把 `x` 整体作为一个元素加进去
`extend(x)`	把 `x` 中的所有元素展开追加进来

示例

复制代码

lst = []
lst.append([1,2])   # → [[1,2]]
lst.extend([1,2])   # → [1,2]

复制代码

# 2️⃣ 步骤二：统计概率参数 π（初始）、A（转移）、B（发射）

# 初始化计数器
start_counts = Counter()              # 初始标签频次：统计每个标签作为句首的频次
trans_counts = defaultdict(Counter)  # 状态转移频次：前一个标签 → 当前标签的频次
emit_counts = defaultdict(Counter)   # 发射频次：标签 → 对应汉字的出现频次
state_counts = Counter()             # 标签总频次：每种标签一共出现了几次

# 遍历标注后的训练语料，统计频次
for sentence in tagged_data:
    prev_state = None    # 前一个标签初始化为空
    for i, (char, state) in enumerate(sentence):
		    # 四类频次在循环中逐步统计：
        state_counts[state] += 1    #标签总频次（用于归一化发射概率）记录每个标签一共出现了多少次。例如：M 出现了 10 次，B 出现了 8 次。
        emit_counts[state][char] += 1    #发射频次（标签 → 字）,如标签 B 下出现了"观"3次、出现了"大"2次 ，用于计算P(观|B)= B标签下观出现次数/B总出现次数
        if i == 0:
            start_counts[state] += 1  #初始状态频次（句首标签），用于统计一个句子以某标签开头的频率（如有多少句以 B 开头）
        if prev_state:
            trans_counts[prev_state][state] += 1  #状态转移频次（上一个标签 → 当前标签），在标签序列 B → M → E 中，会统计：B → M 出现一次、M → E 出现一次，用于计算P(M∣B)= B→M次数/B总出现次数
        prev_state = state

# 归一化为概率（从频率变为概率）
def normalize(counter):
    total = sum(counter.values())
    return {key: val / total for key, val in counter.items()}
		#把字典里的计数转换为概率。例如：Counter({'B': 30, 'S': 20}) → {'B': 0.6, 'S': 0.4}
		
states = ['B', 'M', 'E', 'S']
start_prob = normalize(start_counts)  #生成最终概率参数，表示一个句子以 B 开头的概率是多少？/以 S 开头的概率是多少？
trans_prob = {s: normalize(trans_counts[s]) for s in trans_counts}   #给定当前标签是 B，下一标签是 M 的概率是多少？/给定当前是 M，下一是 E 的概率是多少？
emit_prob = {s: normalize(emit_counts[s]) for s in emit_counts}  #给定当前标签是 B，输出字"观"的概率是多少？/给定当前标签是 S，输出字"我"的概率是多少？

参数名	含义
`obs`	观测序列，如：['我', '爱', '北京']，是每个字
`states`	状态集合，一般为 ['B', 'M', 'E', 'S']
`start_p`	初始概率字典，表示状态作为句子第一个字的概率
`trans_p`	状态转移概率字典，P(当前状态
`emit_p`	发射概率字典，P(观测值

参数	全称	数学表达	含义示例
`start_p`	初始状态概率	P(s0)	如句子第一个字是 B 的概率
`trans_p`	状态转移概率	P(st∣st−1)	比如 B→M 或 M→E 的概率
`emit_p`	发射（观测）概率	P(xt∣st)	比如状态为 B 时出现字"观"的概率

start_p 是"起点"
trans_p 决定"如何转移"
emit_p 决定"如何生成可观测的字"

3️⃣ 步骤三：Viterbi 解码算法（预测标签序列）

def viterbi(obs, states, start_p, trans_p, emit_p):
'''
V 是一个列表，表示从第 0 到 t 步，每个状态的最大概率
path 记录到达某个状态时最优的路径（用于回溯）
'''
V = [{}] # 概率表，V[t][s] 是在第 t 步达到状态 s 的最大概率
path = {} # path[s]是达到状态 s 时对应的最优路径（状态序列）
复制代码
```
  # 初始化第一步（t = 0）
  for s in states:
```
'''
初始时刻 t=0，字是 obs[0]
对于每一个可能的状态 s，计算 V0(s) = π(s)*Bs(x0)
其中
π(s)：状态 s 作为第一个字的概率
Bs(x0)：状态 s 生成第一个字 x₀ 的概率
注：用 .get(..., 1e-6) 是为了防止字典中找不到键时报错（平滑处理）
'''
V[0][s] = start_p.get(s, 1e-6) * emit_p.get(s, {}).get(obs[0], 1e-6)
path[s] = [s]
复制代码
```
  # 动态规划主循环（t ≥ 1），从 1 到 T-1（也就是从第二个字到最后一个字）
  for t in range(1, len(obs)):
      V.append({})    # 添加第 t 步的概率表
      new_path = {}   # 用于记录新路径
```
'''
内层循环：枚举当前可能状态
ps 是前一个状态（prev_state）
curr_state 是当前状态（j）
枚举所有可能的 ps → curr_state 转移，乘以前一步的最优概率，取最大
'''
for curr_state in states:
max_prob, prev_state = max(
[(V[t - 1][ps] * trans_p.get(ps, {}).get(curr_state, 1e-6) *
emit_p.get(curr_state, {}).get(obs[t], 1e-6), ps)
for ps in states], key=lambda x: x[0])
'''
更新当前状态的最大概率及路径
V[t][curr_state]：记录当前状态的最大概率
new_path[curr_state]：更新最优路径，即在原来的 path[prev_state] 上加上当前状态
'''
V[t][curr_state] = max_prob
new_path[curr_state] = path[prev_state] + [curr_state]
path = new_path #替换路径字典（准备下一轮）
复制代码
```
  # 最终结果,找出最后一个字最优路径的终点状态
  final_state = max(V[-1], key=V[-1].get) #找出最后一步（第 T-1 步）哪个状态概率最大
  return path[final_state]
```

复制代码

# 4️⃣ 步骤四：根据标签还原分词结果

def cut_words(obs, tags):
    result = [] # 存储最终分好的词
    word = ''   # 暂存当前正在拼接的词
    # 每次取出当前的字 c 和它的标签 t，然后分四种情况：
    for i in range(len(obs)):
        c, t = obs[i], tags[i]
        #1.标签是 'B'：词的开头，开始拼接一个新词，保存当前字。
        if t == 'B':
            word = c
        #2.标签是 'M'：词的中间，继续拼接正在构建的词。
        elif t == 'M':
            word += c
        #3.标签是 'E'：词的结尾，完成一个词，将其添加到结果列表中，然后清空 word 缓冲。
        elif t == 'E':
            word += c
            result.append(word)
            word = ''
        #4.标签是 'S'：单字成词，直接将这个字作为一个完整词加入结果。
        elif t == 'S':
            result.append(c)
    #如果句子在最后没遇到 'E'，但拼到一半（如 'B', 'M'）就结束了，这一步是把剩下的 word 补进去，防止遗漏。
    if word:
        result.append(word)
    return result

参数	含义
`obs`	原始字序列（观测序列），如：['观', '音', '山']
`tags`	对应的标签序列，如：['B', 'M', 'E']

示例

输入

复制代码

obs  = ['我', '爱', '北', '京', '天', '安', '门']
tags = ['S', 'S', 'B', 'E', 'B', 'M', 'E']

过程

字	标签	操作	result
我	S	单字词，直接加	['我']
爱	S	单字词，直接加	['我', '爱']
北	B	开始拼词	word = '北'
京	E	结束词，加入 ['北京']	['我', '爱', '北京']
天	B	开始拼词	word = '天'
安	M	拼接中	word = '天安'
门	E	拼完词，加到 result	['我', '爱', '北京', '天安门']

输出

复制代码

['我', '爱', '北京', '天安门']

**解释：**如果句子在最后没遇到 'E'，但拼到一半（如 'B', 'M'）就结束了，这一步是把剩下的 word 补进去，防止遗漏。

复制代码

for i in range(len(obs)):
    c, t = obs[i], tags[i]
    ...
if word:
    result.append(word)

这个问题出现在预测标签不完整或模型输出错误时，最后一组标签不是以 E 结尾的合法词尾，而是卡在中间，比如：

例子：标签未正常以 E 结束

复制代码

obs  = ['中', '华', '人', '民', '共', '和', '国']
tags = ['B', 'M', 'M', 'M', 'M', 'M', 'M']  # 没有 E

按正常规则，应该是：

复制代码

['中', '华', '人', '民', '共', '和', '国']
['B',  'M',  'M',  'M',  'M',  'M',  'E']

实际运行 cut_words()

代码逻辑中：

复制代码

for i in range(len(obs)):
    c, t = obs[i], tags[i]
    ...
if word:
    result.append(word)

因为最后没有遇到 E，所以这一整串字符会缓存在变量 word 里但不会自动加入 result。

但 最后一句 if word: 的判断 会帮你补救，把当前 word 加入最终结果中。

最终输出为：

复制代码

['中华人民共和国']  # 这是临时拼的 word，虽然标签有误，也会保留

总结说明

情况	`word` 状态	是否自动加入？
正常 B-M-E 结束	已加入	✅ 是
中途卡在 B 或 B-M 但没 E	缓存未清空	❌ 否（靠末尾 if word）
标签缺失、模型预测错误等	字拼了一半	✅ 补救保留

这种处理方式是对标签序列异常的"鲁棒性补救机制"，防止模型输出不完整时丢词。

复制代码

# ✅ 测试：分词句子 "我爱观音山"
test_sentence = "我爱观音山"
obs = list(test_sentence)
tags = viterbi(obs, states, start_prob, trans_prob, emit_prob)
words = cut_words(obs, tags)

print("标签序列:", tags)
print("分词结果:", words)

（3）输出结果示例：

复制代码

标签序列: ['S', 'S', 'B', 'M', 'E']
分词结果: ['我', '爱', '观音山']

（4）总结

步骤	内容
1️⃣	把分词语料转成字级 BMES 标签
2️⃣	从标签中统计初始、转移、发射概率
3️⃣	用 Viterbi 算法寻找最优标签路径
4️⃣	根据标签序列切分出词语

NLP基础(八)_马尔可夫模型

4.0 马尔可夫与贝叶斯关系

4.1 基本定义

4.2 常见的马尔可夫模型

4.3 马尔可夫链示意

4.4 应用场景

4.5 隐马尔可夫模型

4.5.1 Viterbi(维特比)算法

4.5.2 HMM 分词步骤

4.5.3 HMM 中文分词示例

3️⃣ 步骤三：Viterbi 解码算法（预测标签序列）