算法基础篇：（五）基础算法之差分——以“空间”换“时间”

前言

在算法学习中，"高效处理区间操作" 是贯穿始终的核心需求之一。当面对 "多次修改数组 / 矩阵的某个区间，最后查询结果" 这类问题时，暴力遍历修改的 O (n) 时间复杂度往往无法满足大数据规模的要求。而差分算法 作为**"空间换时间"**思想的经典体现，能将区间修改操作优化到 O (1)，再结合前缀和完成最终查询，成为解决此类问题的 "利器"。

本文将从差分的基本概念入手，系统讲解一维差分、二维差分的原理、实现步骤、边界处理技巧，并结合洛谷、牛客网等平台的经典例题，手把手教你用 C++ 实现差分算法。下面就让我们正式开始吧！

一、差分算法核心思想：为什么需要差分？

在编程中，我们经常遇到这样的场景：

给长度为 1e5 的数组，执行 1e5 次操作，每次将区间 [l, r] 的元素加 k，最后输出数组；
给 1e3×1e3 的矩阵，执行 1e5 次操作，每次将子矩阵 [x1,y1,x2,y2] 的元素加 k，最后输出矩阵。

如果用暴力方法实现 ------ 每次操作遍历区间内所有元素修改，总时间复杂度会达到 O (q×n) （数组）或O (q×n×m)（矩阵）。当 q=1e5、n=1e5 时，O (1e10) 的时间复杂度会直接超时，完全无法通过测试。

差分算法的核心思路是间接修改、集中计算：

构建差分数组 / 矩阵：通过差分数组记录 "区间修改的变化量"，而非直接修改原始数据；
快速处理区间修改：每次区间修改仅需在差分数组的两个位置操作（O (1) 时间）；
还原原始数据：所有修改完成后，通过 "前缀和" 操作将差分数组还原为最终的原始数据（O (n) 或 O (n×m) 时间）。

这种方式将多次区间修改的时间复杂度从O (q×n) 降至 O (q + n)，极大提升了效率，是处理大规模区间操作的首选算法。

二、一维差分：数组区间修改的 "特效药"

一维差分是差分算法的基础形式，适用于一维数组的区间修改与最终查询场景。

2.1 基本原理

2.1.1 差分数组的定义

对于一维数组a[1...n]（本文统一使用 1-based 下标，避免边界处理麻烦），其差分数组d[1...n+1]（注意：差分数组长度比原数组多 1，用于处理 r=n 的边界）的定义为：

d[1] = a[1]
d[i] = a[i] - a[i-1]（对于 2 ≤ i ≤ n）
d[n+1] = 0（边界初始化，避免越界）

简单来说，差分数组的每个元素d[i]记录了**原数组a[i]与a[i-1]**的差值。

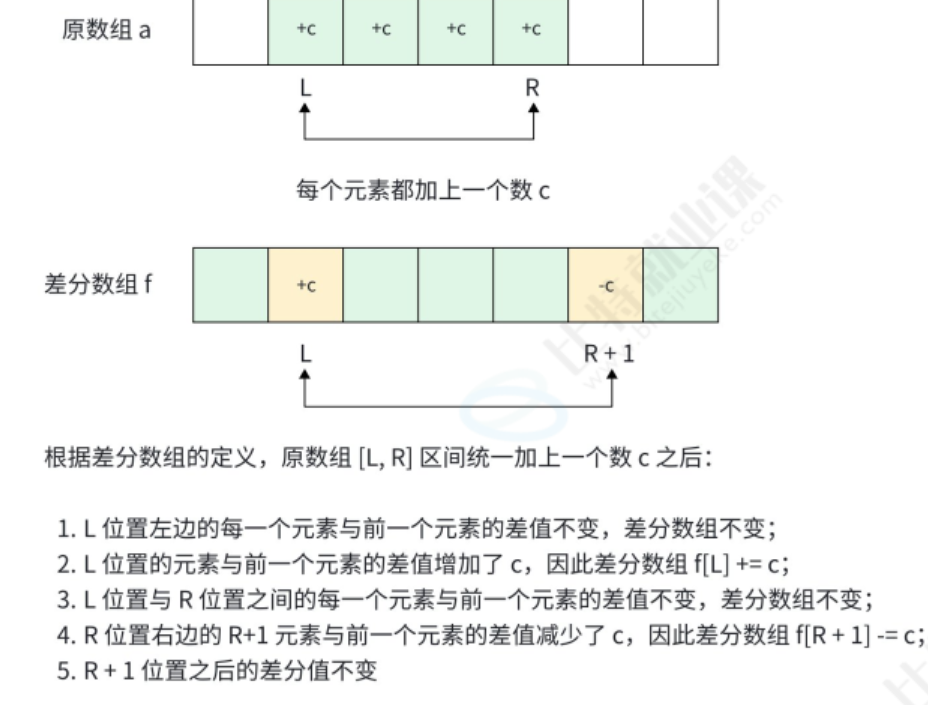
2.1.2 区间修改的核心技巧

假设我们需要将原数组a的区间[l, r]内所有元素加k，如何通过差分数组d实现？

根据差分数组的定义，原数组a是差分数组d的前缀和 （即a[i] = d[1] + d[2] + ... + d[i]）。因此：

要让a[l]到a[r]都加k，只需让差分数组d[l] += k（从l开始，后续前缀和都会增加k）；
为了避免a[r+1]及以后的元素也被加k，需要让d[r+1] -= k（从r+1开始，抵消前面增加的k）。

这两步操作仅需修改差分数组的两个位置，时间复杂度为O(1)，与区间长度无关。

2.1.3 从差分数组还原原数组

所有区间修改完成后，通过 "对差分数组求前缀和" 即可还原出最终的原数组：a[i] = a[i-1] + d[i]（其中a[0] = 0）

推导过程：

差分数组d[i]记录了a[i]与a[i-1]的差值；
累加d[1]到d[i]，正好得到a[i]的最终值。

2.1.4 边界处理关键点

差分数组长度设为**n+1**：当r = n时，r+1 = n+1，不会超出差分数组范围；
初始差分数组构建：若原数组初始非空，需先通过原数组构建初始差分数组（而非直接初始化为 0）。

2.2 一维差分实现步骤

步骤 1：输入原始数组与操作参数

读取数组长度n、操作次数m，然后读取原始数组a[1...n]。

步骤 2：构建初始差分数组

根据差分数组的定义，初始化d[1...n+1]：

d[1] = a[1]
对于2 ≤ i ≤ n：d[i] = a[i] - a[i-1]
d[n+1] = 0

步骤 3：处理所有区间修改操作

对于每次操作(l, r, k)：

d[l] += k
d[r+1] -= k（若r = n，r+1 = n+1，仍在差分数组范围内）

步骤 4：还原最终数组并输出

通过前缀和操作，从差分数组d还原出最终的a数组：

a[0] = 0
对于1 ≤ i ≤ n：a[i] = a[i-1] + d[i]
输出最终的a数组。

2.3 一维差分代码模板（C++）

cpp 复制代码

#include <iostream>
using namespace std;

typedef long long LL;  // 防止数据溢出，必须使用long long
const int N = 1e5 + 10;  // 适配1e5规模的数组

int n, m;
LL a[N];    // 原始数组
LL d[N + 2];// 差分数组（长度n+2，处理r=n的边界）

int main() {
    // 加速输入输出（大数据场景必备）
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    // 步骤1：输入原始数组
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) {
        cin >> a[i];
    }

    // 步骤2：构建初始差分数组
    d[1] = a[1];
    for (int i = 2; i <= n; ++i) {
        d[i] = a[i] - a[i - 1];
    }
    d[n + 1] = 0;  // 边界初始化

    // 步骤3：处理m次区间修改
    while (m--) {
        int l, r;
        LL k;
        cin >> l >> r >> k;
        d[l] += k;
        d[r + 1] -= k;
    }

    // 步骤4：还原最终数组并输出
    LL current = 0;  // 记录当前前缀和
    for (int i = 1; i <= n; ++i) {
        current += d[i];
        cout << current << " ";
    }
    cout << endl;

    return 0;
}

2.4 一维差分常见问题与解决方案

问题 1：数据溢出

现象：当数组元素较大或修改次数较多时，d[i]或current（前缀和）超出int范围；
解决方案：差分数组、原始数组、临时变量（如current）均使用long long类型，int最大值约 2e9，无法满足 1e5 次修改（每次加 1e9）的需求。

问题 2：边界越界

现象：当r = n时，d[r+1] = d[n+1]，若差分数组长度为n，会导致越界；
解决方案：差分数组长度设为n+2（或至少n+1），确保r+1不会超出范围。

问题 3：初始差分数组构建错误

现象：直接将差分数组初始化为 0，未根据原始数组构建初始差值；
解决方案：严格按照d[1] = a[1]、**d[i] = a[i] - a[i-1]**的公式构建，若原始数组初始为 0，则可直接初始化差分数组为 0。

2.5 一维差分经典例题：海底高铁（洛谷 P3406）

题目来源：洛谷 P3406 海底高铁

题目描述

某高铁经过N个城市，相邻城市间的铁路段有两种购票方式：

纸质票：每次乘坐第i段铁路需花费A_i元；
IC 卡：购买 IC 卡需C_i元工本费，每次乘坐扣B_i元（B_i < A_i）。

现在有M个城市的访问序列P_1, P_2, ..., P_M，乘客从P_1出发，依次前往P_2, ..., P_M，求最少总花费（包含购票、买卡费用）。

输入描述

第一行：两个整数**N（城市数）、M（访问城市数）**；
第二行：M个整数，代表访问序列**P_1 ~ P_M**；
接下来N-1行：每行三个整数**A_i, B_i, C_i**（第i段铁路的纸质票价格、IC 卡单次价格、IC 卡工本费）。

输出描述

一个整数，代表最少总花费。

示例输入

复制代码

9 10
3 1 4 1 5 9 2 6 5 3
200 100 50
300 299 100
500 200 500
345 234 123
100 50 100
600 100 1
450 400 80
2 1 10

示例输出

复制代码

题目链接： https://www.luogu.com.cn/problem/P3406

解法思路

问题转化 ：首先需要计算每段铁路的乘坐次数cnt[i]（第i段铁路连接城市i和i+1）；
差分求乘坐次数 ：访问序列中，从P_i到P_{i+1}会经过min(P_i,P_{i+1})到max(P_i,P_{i+1})-1的所有铁路段，因此对差分数组d执行d[l] += 1、d[r+1] -= 1（l = min(P_i,P_{i+1})，r = max(P_i,P_{i+1})-1），最后通过前缀和得到cnt[i]；
计算最小花费 ：对每段铁路，比较 "纸质票总花费（A_i * cnt[i]）" 和 "IC 卡总花费（C_i + B_i * cnt[i]）"，取较小值累加。

代码实现

cpp 复制代码

#include <iostream>
#include <algorithm>  // 用于min、max函数
using namespace std;

typedef long long LL;
const int N = 1e5 + 10;  // N<=1e5，适配题目规模

int n, m;
LL d[N];  // 差分数组，计算每段铁路的乘坐次数
LL cnt[N];// 每段铁路的乘坐次数

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    // 步骤1：输入城市数、访问次数和访问序列
    cin >> n >> m;
    int prev;  // 上一个访问的城市
    cin >> prev;
    for (int i = 2; i <= m; ++i) {
        int curr;
        cin >> curr;
        // 计算当前行程经过的铁路段范围[l, r]
        int l = min(prev, curr);
        int r = max(prev, curr) - 1;
        // 差分更新：乘坐次数+1
        d[l] += 1;
        d[r + 1] -= 1;
        prev = curr;
    }

    // 步骤2：通过前缀和得到每段铁路的乘坐次数cnt
    LL current = 0;
    for (int i = 1; i <= n - 1; ++i) {
        current += d[i];
        cnt[i] = current;
    }

    // 步骤3：计算最小总花费
    LL total = 0;
    for (int i = 1; i <= n - 1; ++i) {
        LL A, B, C;
        cin >> A >> B >> C;
        // 比较纸质票和IC卡的花费，取最小值
        LL cost_ticket = A * cnt[i];
        LL cost_ic = C + B * cnt[i];
        total += min(cost_ticket, cost_ic);
    }

    cout << total << endl;

    return 0;
}

算法分析

时间复杂度：O (N + M)，处理访问序列 O (M)，计算乘坐次数 O (N)，计算花费 O (N)，完全满足 N、M<=1e5 的规模；
空间复杂度：O (N)，存储差分数组和乘坐次数数组；
核心亮点：用差分快速计算多段区间的 "次数累加"，避免暴力遍历每段行程的铁路段，效率提升显著。

三、二维差分：矩阵区间修改的 "高效工具"

一维差分适用于数组，而二维差分是其在矩阵中的扩展，用于快速处理 "多次修改子矩阵、最后查询矩阵" 的问题。

3.1 基本原理

3.1.1 二维差分数组的定义

对于n行m列的矩阵a[1...n][1...m]，其二维差分数组d[1...n+1][1...m+1] （边界多 1 行 1 列）的定义为：d[i][j] = a[i][j] - a[i-1][j] - a[i][j-1] + a[i-1][j-1]

推导思路 ：类比一维差分 "记录相邻元素差值"，二维差分记录 "当前位置与上方、左方、左上位置的差值关系"，确保对d求前缀和后能还原出a。

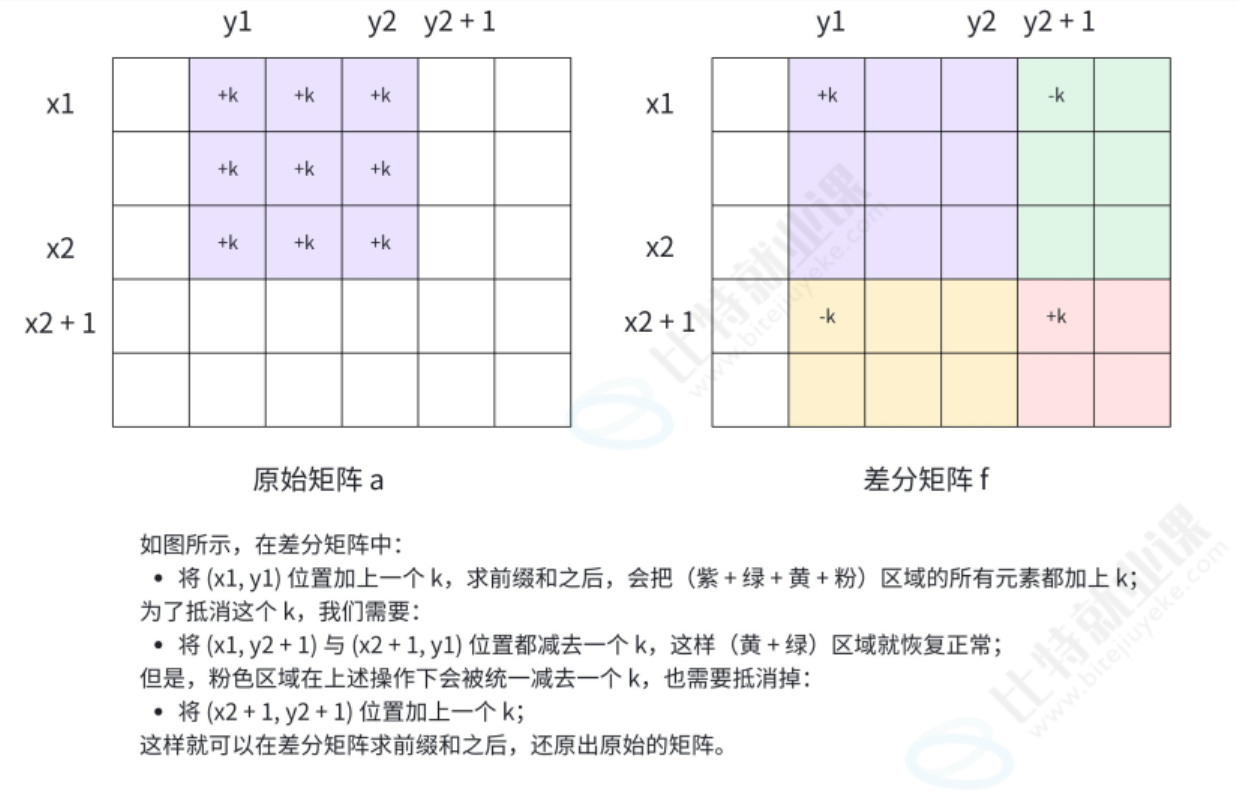
3.1.2 子矩阵修改的核心技巧

假设需要将矩阵a中以(x1,y1)为左上角、(x2,y2)为右下角的子矩阵内所有元素加k，如何通过二维差分数组d实现？

根据二维前缀和的性质（a是d的二维前缀和），我们需要让子矩阵内的所有元素在求前缀和时都增加k，同时不影响子矩阵外的元素。具体操作如下：

d[x1][y1] += k：从(x1,y1)开始，后续二维前缀和都会增加k；

d[x1][y2+1] -= k：抵消y2+1列及以后的增加量，避免右方区域受影响；

d[x2+1][y1] -= k：抵消x2+1行及以后的增加量，避免下方区域受影响；

d[x2+1][y2+1] += k：(x2+1,y2+1)位置被前两步抵消了两次，需加回一次k，恢复平衡。

这四步操作仅需修改差分数组的 4 个位置，时间复杂度为O(1)，与子矩阵的大小无关。

3.1.3 从二维差分数组还原原矩阵

所有子矩阵修改完成后，通过 "对二维差分数组求两次前缀和"（先每行求前缀和，再每列求前缀和，或反之）还原出最终的原矩阵：

行前缀和：对每一行i，d[i][j] += d[i][j-1]（j从 2 到m）；

列前缀和：对每一列j，d[i][j] += d[i-1][j]（i从 2 到n）；

最终**d[i][j]即为原矩阵a[i][j]**的最终值。

3.1.4 边界处理关键点

二维差分数组大小设为**(n+2)×(m+2)：确保x2+1 ≤ n+1、y2+1 ≤ m+1**，避免越界；
初始差分数组构建：若原矩阵初始非空，需根据原矩阵计算初始差分，而非直接初始化为 0。

3.2 二维差分实现步骤

步骤 1：输入原始矩阵与操作参数

读取矩阵的行数n、列数m、操作次数q，然后读取n行m列的原始矩阵a。

步骤 2：构建初始二维差分数组

初始化**d[(n+2)×(m+2)]**为 0，根据原始矩阵a计算初始差分：对于每个i（1≤i≤n）和j（1≤j≤m）：d[i][j] = a[i][j] - a[i-1][j] - a[i][j-1] + a[i-1][j-1]（注：a[0][j]和a[i][0]均视为 0）

步骤 3：处理所有子矩阵修改操作

对于每次操作(x1,y1,x2,y2,k)：

d[x1][y1] += k

d[x1][y2+1] -= k

d[x2+1][y1] -= k

d[x2+1][y2+1] += k

步骤 4：还原最终矩阵并输出

对差分数组d求行前缀和：对于每一行i（1≤i≤n），从j=2到m：d[i][j] += d[i][j-1]
对差分数组d求列前缀和：对于每一列j（1≤j≤m），从i=2到n：d[i][j] += d[i-1][j]
输出d[1...n][1...m]（即最终的原矩阵）。

3.3 二维差分代码模板（C++）

cpp 复制代码

#include <iostream>
using namespace std;

typedef long long LL;
const int N = 1010;  // 适配1e3×1e3的矩阵（n,m<=1e3）

int n, m, q;
LL a[N][N];    // 原始矩阵
LL d[N + 2][N + 2];// 二维差分数组（(n+2)×(m+2)）

// 子矩阵修改：给(x1,y1)到(x2,y2)的子矩阵加k
void insert(int x1, int y1, int x2, int y2, LL k) {
    d[x1][y1] += k;
    d[x1][y2 + 1] -= k;
    d[x2 + 1][y1] -= k;
    d[x2 + 1][y2 + 1] += k;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    // 步骤1：输入原始矩阵
    cin >> n >> m >> q;
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            cin >> a[i][j];
        }
    }

    // 步骤2：构建初始二维差分数组
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            insert(i, j, i, j, a[i][j]);  // 单个元素修改等价于子矩阵(i,j,i,j)加a[i][j]
        }
    }

    // 步骤3：处理q次子矩阵修改
    while (q--) {
        int x1, y1, x2, y2;
        LL k;
        cin >> x1 >> y1 >> x2 >> y2 >> k;
        insert(x1, y1, x2, y2, k);
    }

    // 步骤4：还原最终矩阵（行前缀和 + 列前缀和）
    // 行前缀和
    for (int i = 1; i <= n; ++i) {
        for (int j = 2; j <= m; ++j) {
            d[i][j] += d[i][j - 1];
        }
    }
    // 列前缀和
    for (int j = 1; j <= m; ++j) {
        for (int i = 2; i <= n; ++i) {
            d[i][j] += d[i - 1][j];
        }
    }

    // 输出最终矩阵
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            cout << d[i][j] << " ";
        }
        cout << endl;
    }

    return 0;
}

3.4 二维差分关键优化：初始差分的简化构建

在步骤 2 中，构建初始差分数组时，我们可以利用insert函数的 "单个元素修改" 功能（子矩阵左上角和右下角均为(i,j)），直接将a[i][j]作为k传入insert(i,j,i,j,a[i][j])，避免手动计算**d[i][j] = a[i][j] - a[i-1][j] - a[i][j-1] + a[i-1][j-1]**的复杂公式，减少代码出错概率。

这种方式的原理是：初始时差分数组d全为 0，对每个(i,j)执行 "子矩阵(i,j,i,j)加a[i][j]"，等价于构建了初始的差分数组，与手动计算结果完全一致。

3.5 二维差分经典例题：地毯（洛谷 P3397）

题目来源：洛谷 P3397 地毯

题目描述

在n×n的格子上有m个地毯，每个地毯覆盖以(x1,y1)为左上角、(x2,y2)为右下角的子矩阵。求每个格子被多少个地毯覆盖。

输入描述

第一行：两个整数n（格子大小）、m（地毯数）；
接下来m行：每行四个整数x1,y1,x2,y2（地毯的左上角和右下角坐标）。

输出描述

n行，每行n个整数，第i行第j列的整数表示(i,j)格子被覆盖的次数。

示例输入

cpp 复制代码

示例输出

复制代码

题目链接： https://www.luogu.com.cn/problem/P3397

解法思路

问题转化 ：每个地毯覆盖子矩阵(x1,y1,x2,y2)，等价于 "将该子矩阵的每个元素加 1"，最终查询每个元素的值；
二维差分实现 ：使用二维差分数组d，每次地毯覆盖操作对应insert(x1,y1,x2,y2,1)；
还原矩阵 ：所有地毯操作完成后，对d求行前缀和与列前缀和，得到每个格子的覆盖次数。

代码实现

cpp 复制代码

#include <iostream>
using namespace std;

const int N = 1010;  // n<=1e3，适配题目规模

int n, m;
int d[N + 2][N + 2];// 二维差分数组

// 子矩阵加1操作
void insert(int x1, int y1, int x2, int y2) {
    d[x1][y1] += 1;
    d[x1][y2 + 1] -= 1;
    d[x2 + 1][y1] -= 1;
    d[x2 + 1][y2 + 1] += 1;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    cin >> n >> m;
    for (int i = 0; i < m; ++i) {
        int x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        insert(x1, y1, x2, y2);
    }

    // 行前缀和
    for (int i = 1; i <= n; ++i) {
        for (int j = 2; j <= n; ++j) {
            d[i][j] += d[i][j - 1];
        }
    }

    // 列前缀和
    for (int j = 1; j <= n; ++j) {
        for (int i = 2; i <= n; ++i) {
            d[i][j] += d[i - 1][j];
        }
    }

    // 输出结果
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= n; ++j) {
            cout << d[i][j] << " ";
        }
        cout << endl;
    }

    return 0;
}

算法分析

时间复杂度：O (n² + m) ，处理m个地毯 O (m)，还原矩阵 O (n²)，n<=1e3时n²=1e6，完全满足时间要求；
空间复杂度：O (n²)，存储二维差分数组；
优势：相比暴力遍历每个地毯的子矩阵（O (m×n²)），二维差分将时间复杂度降低了许多，是解决此类问题的最佳方案。

四、差分与前缀和的关系：互逆运算的协同应用

差分与前缀和是互逆运算，二者结合能完美解决 "多次区间修改 + 多次区间查询" 的复杂问题，这也是算法竞赛中最常见的场景之一。

4.1 互逆关系的数学表达

差分是前缀和的逆运算：
- 对数组a求差分得到d，再对d求前缀和，得到的仍是a；
- 公式表示：prefix_sum(diff(a)) = a。
前缀和是差分的逆运算：
- 对数组d求前缀和得到a，再对a求差分，得到的仍是d；
- 公式表示：diff(prefix_sum(d)) = d。

4.2 协同应用场景：多次区间修改 + 多次区间查询

当需要同时处理 "多次区间修改" 和 "多次区间查询" 时，单独使用差分或前缀和都无法满足需求，需二者结合：

用差分处理区间修改：每次修改 O (1)，总时间 O (q)；
用前缀和处理区间查询：先将差分数组还原为原始数组（O (n)），再构建前缀和数组（O (n)），每次查询 O (1)，总时间 O (n + q')（q' 为查询次数）。

示例：一维数组的 "修改 + 查询"

假设需要对数组a执行m次区间修改（每次[l,r]加k）和q次区间查询（每次查询[l,r]的和），代码实现如下：

cpp 复制代码

#include <iostream>
using namespace std;

typedef long long LL;
const int N = 1e5 + 10;

int n, m, q;
LL d[N + 2];  // 差分数组
LL pre[N];    // 前缀和数组（用于查询）

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    cin >> n >> m >> q;

    // 处理m次区间修改
    for (int i = 0; i < m; ++i) {
        int l, r;
        LL k;
        cin >> l >> r >> k;
        d[l] += k;
        d[r + 1] -= k;
    }

    // 还原原始数组并构建前缀和数组
    LL current = 0;
    pre[0] = 0;
    for (int i = 1; i <= n; ++i) {
        current += d[i];
        pre[i] = pre[i - 1] + current;  // pre[i]是前i个元素的和
    }

    // 处理q次区间查询
    while (q--) {
        int l, r;
        cin >> l >> r;
        cout << pre[r] - pre[l - 1] << endl;
    }

    return 0;
}

4.3 二维场景的协同应用

对于矩阵的 "多次子矩阵修改 + 多次子矩阵查询"，同样也可以结合二维差分与二维前缀和：

用二维差分处理子矩阵修改（O (1) 每次）；
还原矩阵后，构建二维前缀和数组（O (n×m)）；
每次子矩阵查询通过二维前缀和实现（O (1) 每次）。

五、差分算法常见误区与优化技巧

5.1 常见误区

误区 1：二维差分公式记错

当修改子矩阵时遗漏了某一步操作（如忘记d[x2+1][y2+1] += k），导致还原后矩阵错误；
解决方案：牢记二维差分的 "四步操作"------"加左上、减右上、减左下、加右下"，可联想为 "抵消多余修改" 的逻辑，确保子矩阵外的元素不受影响。

误区 2：差分数组大小不足

现象：一维差分数组长度为n，导致r=n时d[r+1]越界；二维差分数组为n×m，导致x2=n或y2=m时越界；
解决方案：一维差分数组长度设为n+2，二维差分数组设为(n+2)×(m+2)，预留足够的边界空间。

误区 3：数据类型使用错误

现象：使用int类型存储差分数组或前缀和，导致数据溢出；
解决方案：无论一维还是二维，差分数组、前缀和数组、临时变量均使用long long类型，尤其是处理 1e5 规模的修改时。

误区 4：还原矩阵时前缀和顺序错误

现象：二维差分还原时先求列前缀和，再求行前缀和，导致结果错误；
解决方案：二维前缀和的顺序不影响结果（先 row 后 column 或反之均可），但需确保每行 / 每列的前缀和计算完整，避免遗漏。

5.2 优化技巧

技巧 1：空间优化

一维差分：若无需保留原始差分数组，可直接在差分数组上计算前缀和并输出，无需额外存储原始数组；
二维差分：同理，还原矩阵时可直接在差分数组上修改，无需额外开辟空间存储最终矩阵。

技巧 2：输入输出优化

当数据规模较大（如n=1e5或n=1e3）时，必须使用ios::sync_with_stdio(false); cin.tie(nullptr);加速输入输出，否则cin/cout的默认同步机制会导致 TLE。

技巧 3：函数封装

将差分的核心操作（如一维的区间修改、二维的子矩阵修改）封装为函数（如前文的insert函数），可减少代码冗余，降低出错概率，提高代码可读性。

技巧 4：边界预处理

对于二维差分，可提前将差分数组的0行和0列初始化为 0，避免处理i=1或j=1时的边界判断，简化代码逻辑。

总结

差分算法的应用远不止本文介绍的内容，在后续的前缀和优化 DP、滑动窗口等算法中，差分也会作为辅助工具出现。因此，熟练掌握差分算法，不仅能解决当前的基础问题，更能为后续的算法学习打下坚实基础。

希望本文能帮助大家深入理解差分算法的原理与应用。如果在学习过程中遇到问题，欢迎在评论区留言讨论！

算法基础篇：（五）基础算法之差分——以“空间”换“时间”

目录

前言

一、差分算法核心思想：为什么需要差分？

二、一维差分：数组区间修改的 "特效药"

2.1 基本原理

2.1.1 差分数组的定义

2.1.2 区间修改的核心技巧

2.1.3 从差分数组还原原数组

2.1.4 边界处理关键点

2.2 一维差分实现步骤

步骤 1：输入原始数组与操作参数

步骤 2：构建初始差分数组

步骤 3：处理所有区间修改操作

步骤 4：还原最终数组并输出

2.3 一维差分代码模板（C++）

2.4 一维差分常见问题与解决方案

问题 1：数据溢出

问题 2：边界越界

问题 3：初始差分数组构建错误

2.5 一维差分经典例题：海底高铁（洛谷 P3406）

题目来源：洛谷 P3406 海底高铁

题目描述

输入描述

输出描述

示例输入

示例输出

解法思路

代码实现

算法分析

三、二维差分：矩阵区间修改的 "高效工具"

3.1 基本原理

3.1.1 二维差分数组的定义

3.1.2 子矩阵修改的核心技巧

3.1.3 从二维差分数组还原原矩阵

3.1.4 边界处理关键点

3.2 二维差分实现步骤

步骤 1：输入原始矩阵与操作参数

步骤 2：构建初始二维差分数组

步骤 3：处理所有子矩阵修改操作

步骤 4：还原最终矩阵并输出

3.3 二维差分代码模板（C++）

3.4 二维差分关键优化：初始差分的简化构建

3.5 二维差分经典例题：地毯（洛谷 P3397）

题目来源：洛谷 P3397 地毯

题目描述

输入描述

输出描述

示例输入

示例输出

解法思路

代码实现

算法分析

四、差分与前缀和的关系：互逆运算的协同应用

4.1 互逆关系的数学表达

4.2 协同应用场景：多次区间修改 + 多次区间查询

示例：一维数组的 "修改 + 查询"

4.3 二维场景的协同应用

五、差分算法常见误区与优化技巧

5.1 常见误区

误区 1：二维差分公式记错

误区 2：差分数组大小不足

误区 3：数据类型使用错误

误区 4：还原矩阵时前缀和顺序错误

5.2 优化技巧

技巧 1：空间优化

技巧 2：输入输出优化

技巧 3：函数封装

技巧 4：边界预处理

总结