lc1959
定义dp[i][j]:前i+1个元素(下标0~i)分成j段,最少浪费的空间
递推公式:
dp[i][j] = min(dp[k-1][j-1] + g[k][i])(k从1到i),k=0时dp[-1][j-1]视为0
++g[k][i]是预处理的"区间i~j按最大值扩容的浪费量"++
- 初始化:
dp数组全设为无穷大(INF),表示初始状态无有效解
- 遍历顺序:
先遍历元素下标i(0到n-1),再遍历分段数j(1到k+1),最后遍历分割点k(0到i),确保子问题先求解
- 结果:dp[n-1][k+1],即所有元素分成k+1段(对应k次扩容)的最小浪费空间
class Solution {
public:
int minSpaceWastedKResizing(vector<int>& nums, int k) {
const int n = nums.size();
const int m = k + 2;
const int INF = 0x3f3f3f3f;
int g[n][n]; //预处理数组
for (int i = 0; i < n; ++i) {
int best = -INF; //准备用于记录区间内最大值
int total = 0; //区间和
for (int j = i; j < n; ++j) {
best = max(best, nums[j]); //更新最大值
total += nums[j]; //更新区间和
g[i][j] = best * (j - i + 1) - total; //得到权值
}
}
int dp[n][m]; //表示dp[i][j]表示前i个点分成j份的最小权值
memset(dp, INF, sizeof(dp));
for (int i = 0; i < n; ++i) //遍历每一个点
for (int j = 1; j < m; ++j) //遍历切割次数
for (int k = 0; k <= i; ++k) //切割成j段从切割成j - 1段转移而来
++dp[i][j] = min(dp[i][j], (k == 0 ? 0 : dp[k - 1][j - 1]) + g[k][i]);++
return dp[n - 1][k + 1];
}
};
lcr20
dp五步
定义dp[i][j]:表示字符串s从下标i到j的子串是否是回文串(true/false)
确定递推公式:
s[i]==s[j]时,i==j(单个字符)或i+1==j(相邻字符)直接是回文;否则看dp[i+1][j-1](内部子串是否回文);
s[i]!=s[j]则一定不是回文。
初始化:创建n×n的false数组,后续通过递推填充true情况
遍历顺序:
从后往前遍历i(保证i+1先算)
j从i开始往后(保证j>=i,子串有效)
- 计算结果:统计++dp数组中所有true的个数,++就是回文子串总数。
class Solution {
public:
int countSubstrings(string s) {
int n=s.size();
vector<vector<bool>> dp(n,vector<bool>(n,false));
++for(int i=n-1;i>=0;i--)
{
for(int j=i;j<n;j++)
{++
if(s[i]!=s[j])
dp[i][j]=false;
if(s[i]==s[j])
{
if(i==j)
dp[i][j]=true;//重合
else if(i+1==j)
dp[i][j]=true;//相邻
else
dp[i][j]=dp[i+1][j-1];
//不存在越界 因为重合和相邻的情况
//已经给这个二维数组 填好了一部分
}
}
}
int ret=0;
for(auto d:dp)
ret+=reduce(d.begin(),d.end(),0);
return ret;
}
};
lc1611
格雷码:相邻两位做异或,可以得到变化位
格雷码是相邻数二进制表示仅差1位的编码(无多余位变化,防误读

class Solution {
public:
int minimumOneBitOperations(int n) {
int mask = n;
while (mask) {
mask >>= 1;
n ^= mask;
}
return n;
}
};
生成格雷码
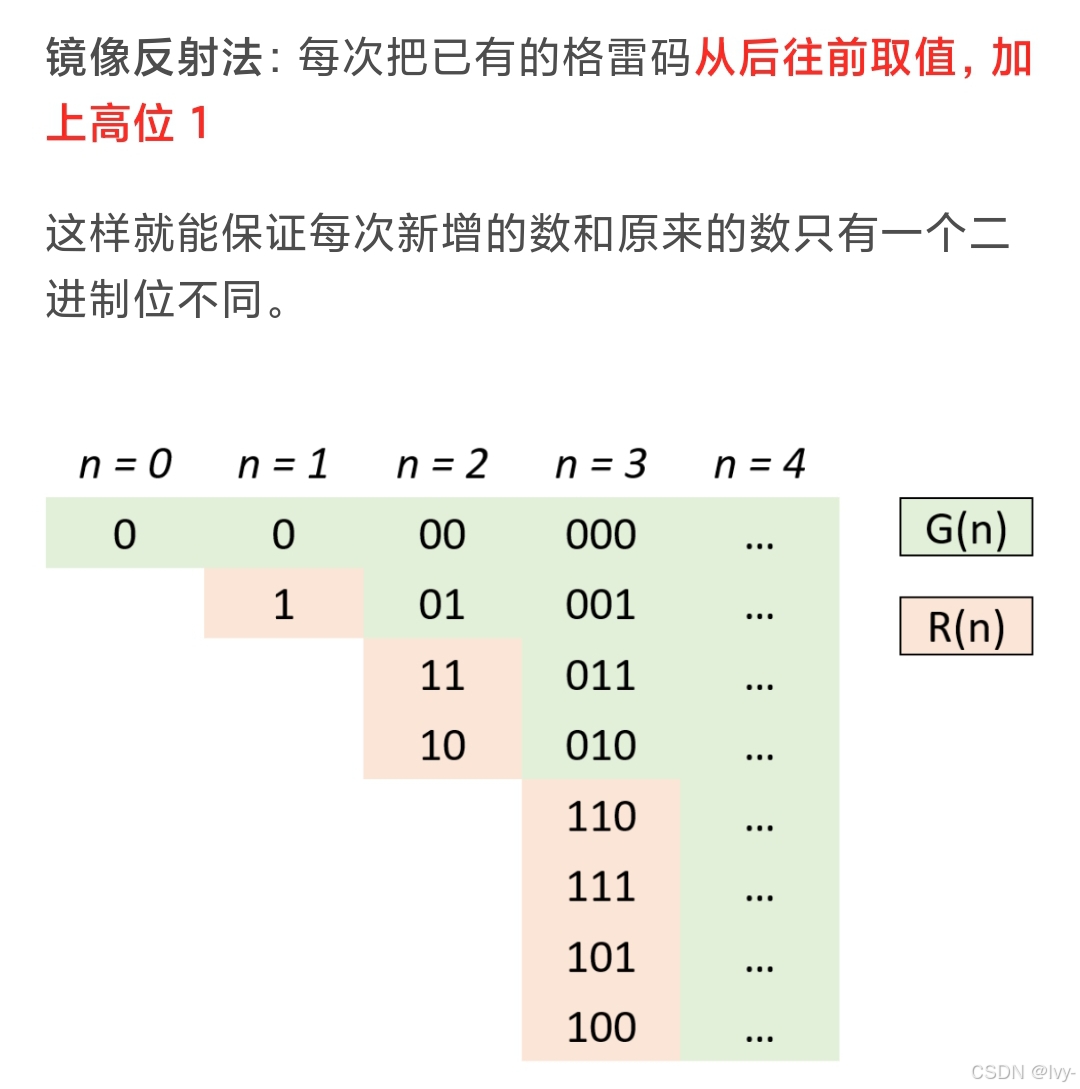
class Solution {
public:
//每次把已有的格雷码从后往前取值,加上高位 1
vector<int> grayCode(int n)
{
vector<int> ret;
ret.push_back(0); //初始化
int head=1;
//层数看待
for(int i=0;i<n;i++)
{
for(int j=ret.size()-1;j>=0;j--)
{
ret.push_back(head+ret[j]);
}
head<<=1;
}
return ret;
}
};
lc1155
dp[i][j] 表示使用 i 个骰子,总和为 j 时的组合方式数。
公式
对于第 i 个骰子,它的点数可以是 1~k 中的一个。假设第 i 个骰子掷出的点数是 f ,那么前 i-1 个骰子的总和需要是 j - f 。因此递推公式为:
dp[i][j] = (dp[i][j] + dp[i-1][j - f]) % MOD (其中 ++f 从 1 遍历到 k ,且 j - f ≥ 0 )。++
- 初始化DP数组
dp[0][0] = 1 :表示0个骰子,总和为0的情况只有1种(没有骰子时,自然总和为0)。
其他 dp[0][j] ( j>0 )和 dp[i][0] ( i>0 )都初始化为0,因为这些情况不可能出现
- 确定遍历顺序
先遍历骰子的数量 i (从1到 n ),因为每个骰子的状态依赖于前一个骰子的状态。
再遍历目标和 j (从1到 target ),因为当前总和 j 依赖于更小的总和 j - f 。
最后遍历每个骰子的点数 f (从1到 k ),枚举当前骰子可能的点数。
- return dp[n][target];
class Solution
{
const int MOD = 1e9 + 7;
public:
int numRollsToTarget(int n, int k, int target) {
vector<vector<int>> dp(n + 1, vector<int>(target + 1, 0));
dp[0][0] = 1;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= target; ++j) {
++for (int f = 1; f <= k; ++f) {
if (j - f >= 0) {
dp[i][j] = (dp[i][j] + dp[i - 1][j - f]) % MOD;++
}
}
}
}
return dp[n][target];
}
};
记忆化搜索
class Solution {
public:
int numRollsToTarget(int n, int k, int target) {
if (target < n || target > n * k) {
return 0; // 无法组成 target
}
constexpr int MOD = 1'000'000'007;
vector memo(n + 1, vector<int>(target - n + 1, -1)); // -1 表示没有计算过
auto dfs = [&](this auto&& dfs, int i, int j) -> int {
if (i == 0) {
return j == 0;
}
int& res = memo[i][j]; // 注意这里是引用
if (res != -1) { // 之前计算过
return res;
}
res = 0;
for (int x = 0; x < k && x <= j; x++) { // 掷出了 x
res = (res + dfs(i - 1, j - x)) % MOD;
}
return res;
};
return dfs(n, target - n);
}
};