112.路径总和 - 技术栈

一、题目描述

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

示例 1：

复制代码

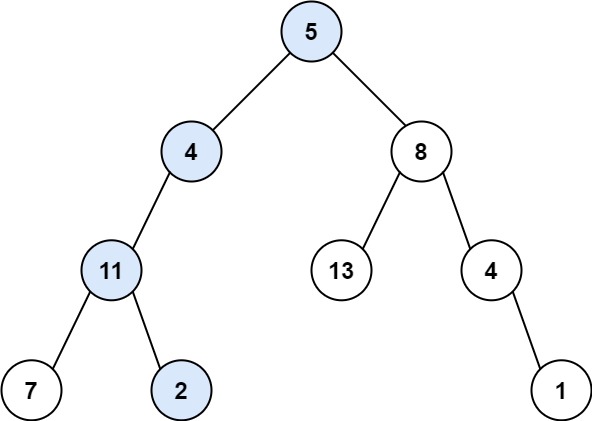
输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

示例 2：

复制代码

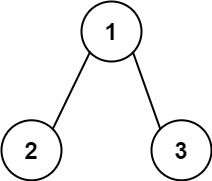
输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。

示例 3：

复制代码

输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。

提示：

树中节点的数目在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000

二、解题思路

核心思路：递归遍历 + 路径和累加

利用二叉树的递归遍历特性，从根节点开始逐步累加路径上的节点值，直到到达叶子节点时校验总和是否等于目标和。

具体逻辑：

终止条件 ：
- 若当前节点为 NULL（空树或遍历到空分支），返回 false（无有效路径）。
- 若当前节点是叶子节点（无左右子节点），判断当前节点值是否等于剩余目标和（初始目标和减去路径上所有前置节点值）。
递归过程 ：
- 非叶子节点时，计算剩余目标和（targetSum - 当前节点值）。
- 递归遍历左、右子树，只要任一子树返回 true，说明存在符合条件的路径，整体返回 true。

优势：

逻辑简洁，直接贴合题目 "根到叶子路径" 的遍历需求。
空间复杂度由递归栈深度决定，无需额外存储路径节点，效率较高。

三、代码实现（C 语言）

cpp 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool hasPathSum(struct TreeNode* root, int targetSum) {
    // 空树直接返回false，无路径可走
    if (root == NULL) {
        return false;
    }
    // 叶子节点：校验当前节点值是否等于剩余目标和
    if (root->left == NULL && root->right == NULL) {
        return root->val == targetSum;
    }
    // 计算剩余目标和，递归遍历左右子树
    int remainingSum = targetSum - root->val;
    return hasPathSum(root->left, remainingSum) || hasPathSum(root->right, remainingSum);
}

四、总结

1. 算法特性

时间复杂度：O (n)，n 为树的节点数，每个节点仅遍历一次。
空间复杂度：O (h)，h 为树的高度。最坏情况（斜树）为 O (n)，平均情况（平衡树）为 O (log n)，由递归栈深度决定。

2. 关键注意点

必须严格区分 "叶子节点"：仅当节点无左右子节点时才判定为叶子，避免将只有一个子节点的节点误判。
空树处理：若根节点为 NULL，无论目标和是否为 0，均返回 false（题目定义 "根到叶子路径" 不存在）。
负数场景兼容：节点值和目标和支持负数，递归过程中直接累加减法，无需额外处理符号问题。

3. 扩展思路

若需避免递归（应对极深的树防止栈溢出），可使用迭代法（栈存储节点和当前路径和），核心逻辑与递归一致，仅将递归栈替换为手动维护的栈结构。