文章目录
- 前言
- [题目 3 哈夫曼编码](#题目 3 哈夫曼编码)
- [题目4 设计LRU缓存结构](#题目4 设计LRU缓存结构)
前言
上一篇传送门:海致星图招聘 数据库内核研发实习生 一轮笔试 总结复盘(1)
这一篇包含两道实际应用型算法题。
题目 3 哈夫曼编码
题目描述:
给出一个有 n 种字符组成的字符串,其中第 i 种字符出现的次数为 aᵢ。请你对该字符串应用哈夫曼编码,使得该字符串的长度尽可能短,求编码后的字符串的最短长度。
输入描述
第一行输入一个整数 n(1 ≤ n ≤ 2・10⁵),表示字符种数。
第二行输入 n 个整数 aᵢ(1 ≤ aᵢ ≤ 10⁹),表示每种字符的出现次数。
输出描述
输出一行一个整数,表示编码后字符串的最短长度。
示例 1输入:
3
1 2 3
输出:
9
说明:
三种字符的哈夫曼编码分别为 "00"、"01"、"1" 时,长度最短,最短长度为 9。
哈夫曼编码基础
哈夫曼编码是一种基于字符出现频率的前缀编码 ,核心是对高频字符分配短编码、低频字符分配长编码,以此最大化压缩效率,其最短编码总长度等价于哈夫曼树的带权路径长度(WPL)。
1. 核心概念
- 前缀编码:任意一个字符的编码都不是其他字符编码的前缀,避免解码时产生歧义(如"0"和"01"就不是合法前缀编码,解码"01"时无法判断是"0+1"还是单独的"01")。
- 哈夫曼树:带权路径长度最短的二叉树,所有字符对应叶子节点,节点权重为字符出现次数。
- 带权路径长度(WPL) :所有叶子节点的权重 × 该节点到根节点的路径长度 之和,公式为:
W P L = ∑ i = 1 n ( w i × l i ) WPL = \sum_{i=1}^n (w_i \times l_i) WPL=i=1∑n(wi×li)
其中 w i w_i wi 为字符出现次数, l i l_i li 为该字符的哈夫曼编码长度。
2. 哈夫曼树的构建步骤
- 将每个字符的出现次数作为权重,构建独立的二叉树节点;
- 每次选取权重最小的两个节点,合并为一个新节点,新节点权重为两个子节点权重之和;
- 将新节点重新加入节点集合,重复步骤2,直到集合中只剩一个节点(哈夫曼树的根节点);
- 从根节点到叶子节点的路径即为编码(左分支为0、右分支为1,或反之)。
如下图例子👇:

3. 核心结论:WPL = 所有非叶子节点权重和
这是哈夫曼编码解题的关键简化思路,也是代码高效实现的核心,我们从原理和示例两层验证:
原理推导
合并两个节点时,新节点为非叶子节点,其权重是两个子节点的和。合并操作意味着两个子节点的路径长度各增加1,因此总WPL会增加「两个子节点的权重和」(即新节点权重)。多次合并后,所有非叶子节点的权重累加和,恰好等于所有叶子节点「权重×路径长度」的总和。
示例验证
我们依然用ABAACDC 字符串进行验证
先统计字符频率
字符:A B C D
频率:3 1 2 1 (对应 a = [3,1,2,1])
传统方式计算WPL
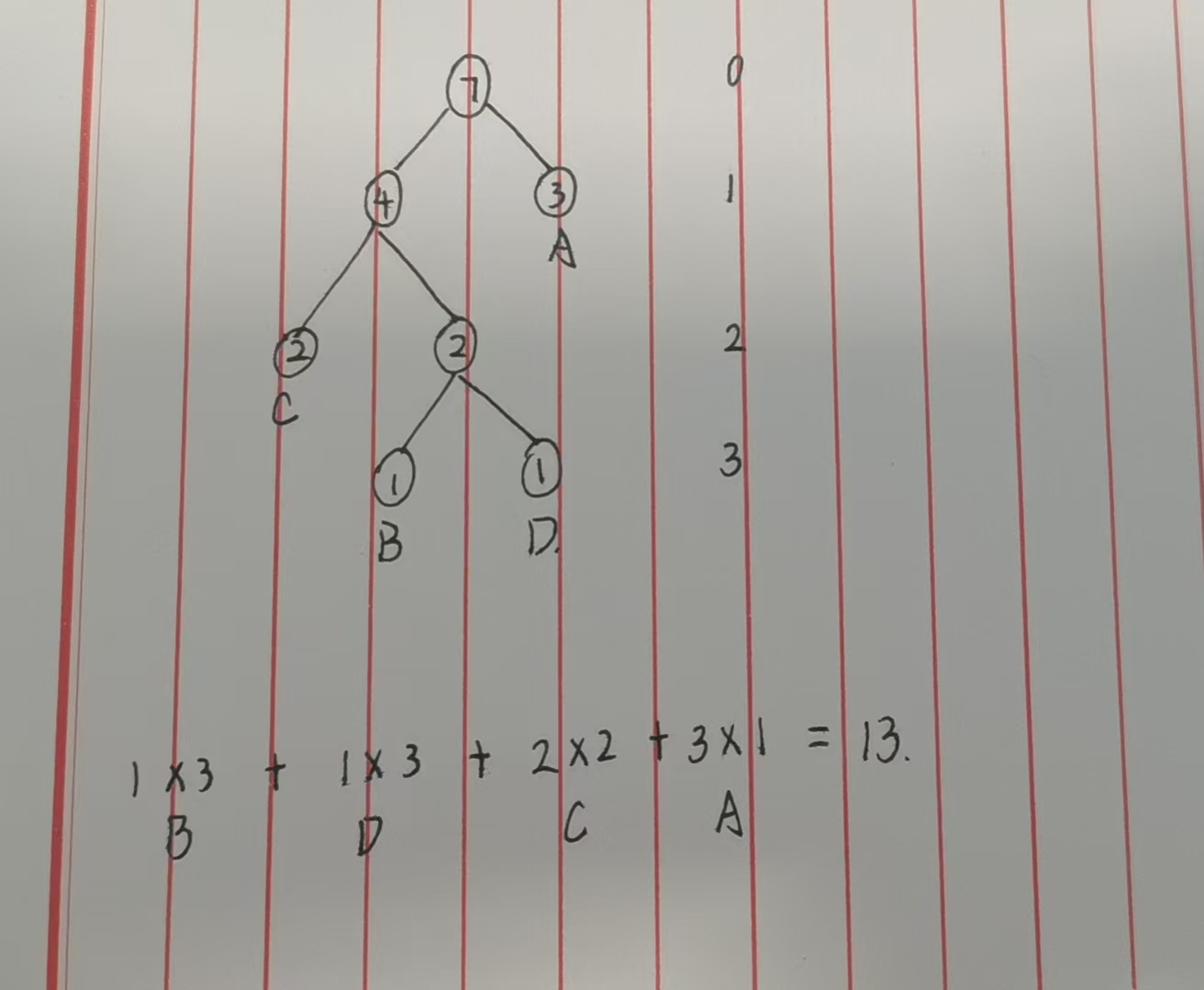
上述方式计算WPL
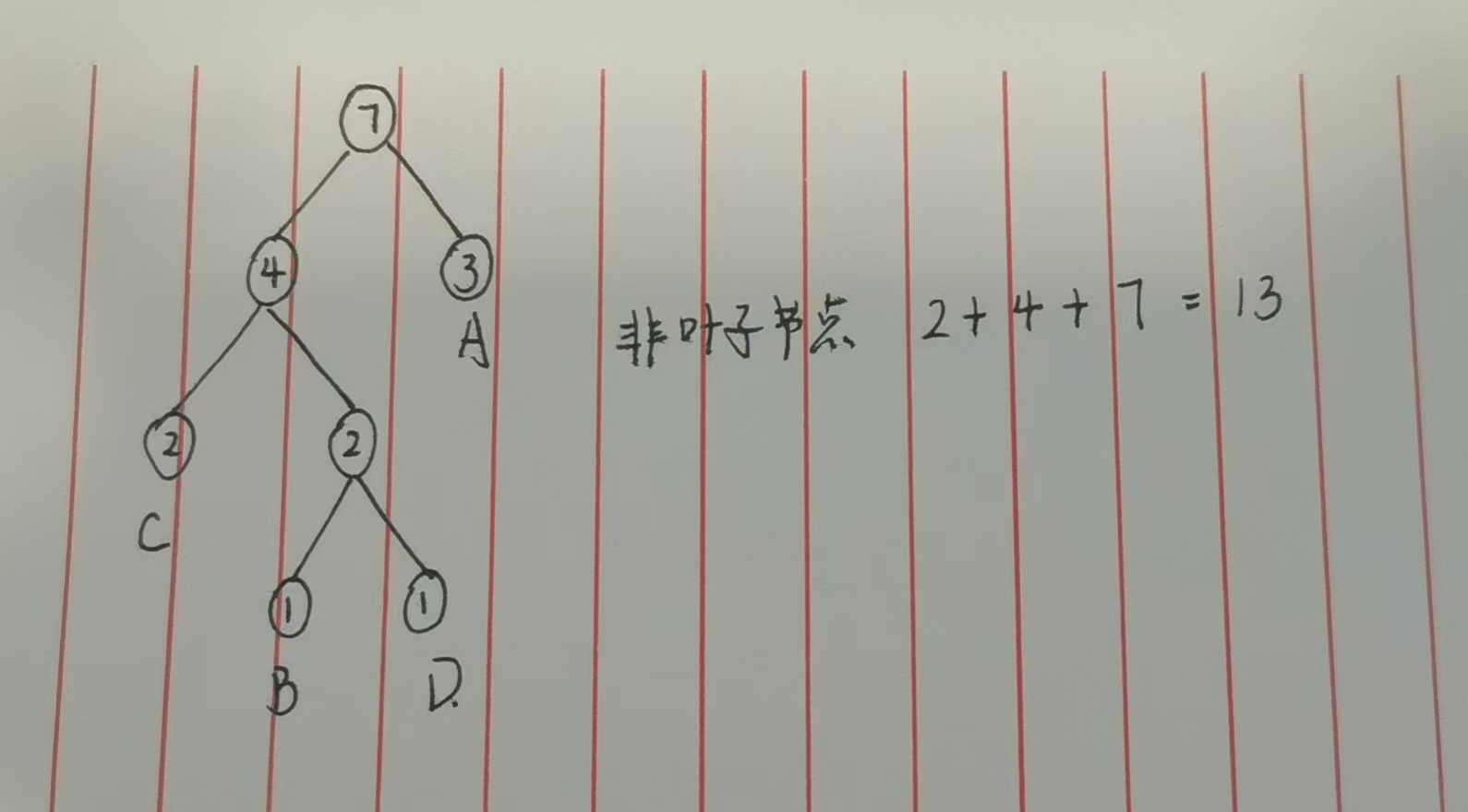
我们会发现两种计算方法的得到的结果是一致的
如果对哈夫曼编码有遗忘的朋友可以看下B站中这两位UP主的视频讲解的非常详细:哈夫曼树和哈夫曼编码, 看完秒懂! 和 数据结构------五分钟搞定哈夫曼树,会求WPL值,不会你打我
算法分析
核心解题思路
基于上述结论,解题无需显式构建哈夫曼树,只需通过反复合并最小权重节点,累加每次合并产生的非叶子节点权重,最终累加和即为最短编码总长度,步骤如下:
- 将所有字符的出现次数放入最小堆,快速获取最小权重;
- 每次从堆中取出两个最小权重,计算合并后的新权重,将新权重累加到总长度;
- 将新权重重新入堆,重复步骤2直到堆中只剩一个节点;
- 累加的总长度即为答案。
数据结构选择:最小堆(优先队列)
解题的关键是频繁快速获取并删除两个最小权重,最小堆是最优选择,原因如下:
- 堆的
top()操作可 O ( 1 ) O(1) O(1)获取最小值,pop()和push()操作时间复杂度为 O ( log k ) O(\log k) O(logk)(k为当前堆大小); - 适配题目数据规模:n最大为 2 × 10 5 2×10^5 2×105,堆操作的时间复杂度可满足时间限制。
注:C++中
priority_queue默认是大根堆,需自定义为小根堆。
边界情况处理
当 n = 1 n=1 n=1时,只有一种字符,无需进行任何合并操作,编码长度为0,因此总长度直接输出0即可。
代码实现
cpp
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
// 定义long long别名,防止溢出(a_i最大1e9,n最大2e5,总和可达1e14)
typedef long long ll;
int main() {
// 输入加速:关闭cin与stdio的同步,解除cin与cout的绑定,处理大数据量必备
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n;
cin >> n;
// 定义最小堆:priority_queue<类型, 底层容器, 比较规则>
priority_queue<ll, vector<ll>, greater<ll>> min_heap;
// 输入字符出现次数并初始化最小堆
for (int i = 0; i < n; ++i) {
ll a;
cin >> a;
min_heap.push(a);
}
ll total_length = 0; // 存储最终最短编码长度(即WPL)
// 合并过程:堆中节点数>1时持续合并,直到只剩根节点
while (min_heap.size() > 1) {
// 取出堆中两个最小的权重节点
ll first = min_heap.top();
min_heap.pop();
ll second = min_heap.top();
min_heap.pop();
// 合并为新节点,权重为两节点之和(非叶子节点权重)
ll merge = first + second;
// 累加非叶子节点权重到总长度,核心等价于更新WPL
total_length += merge;
// 新节点入堆,参与后续合并
min_heap.push(merge);
}
// 输出结果
cout << total_length << endl;
return 0;
}代码逐行核心解释
- 数据类型选择 :使用
long long而非int,因为 a i a_i ai最大为 10 9 10^9 109,n最大为 2 × 10 5 2×10^5 2×105,合并过程中总长度可能达到 10 14 10^{14} 1014,远超int的取值范围( 2 31 − 1 ≈ 2 × 10 9 2^{31}-1≈2×10^9 231−1≈2×109),避免溢出是必做操作; - 输入加速 :
ios::sync_with_stdio(false); cin.tie(nullptr);关闭cin与C语言stdio的同步,解除cin对cout的绑定,能大幅提升大数据量下的输入速度,否则处理 2 × 10 5 2×10^5 2×105个数据时容易超时; - 最小堆定义 :通过
greater<ll>将默认大根堆改为小根堆,确保每次top()能获取当前最小权重; - 合并逻辑:循环条件为堆大小>1,每次合并两个最小节点,累加合并后的权重到总长度,新节点重新入堆,直到堆中只剩根节点;
- 边界处理 :当 n = 1 n=1 n=1时,循环不会执行,
total_length保持0,直接输出即可,无需额外判断。
测试用例验证
- 示例1:输入3 1 2 3 → 合并1+2=3(总长度3),再合并3+3=6(总长度9)→ 输出9;
- 示例2:输入1 5 → 循环不执行,总长度0 → 输出0;
- 常规用例:输入4 3 1 2 1 → 合并1+1=2(总2)→ 合并2+2=4(总6)→ 合并3+4=7(总13)→ 输出13。
时间与空间复杂度分析
- 时间复杂度 : O ( n log n ) O(n \log n) O(nlogn)
堆初始化的时间为 O ( n ) O(n) O(n)(底层基于vector的堆构建);需执行 n − 1 n-1 n−1次合并操作,每次操作包含2次pop()和1次push(),每次堆操作的时间为 O ( log n ) O(\log n) O(logn),总操作时间为 O ( n log n ) O(n \log n) O(nlogn)。 - 空间复杂度 : O ( n ) O(n) O(n),用于存储堆中的所有节点。
实战思考与拓展
常见坑点(必避)
- 溢出问题 :忘记使用
long long,仅用int存储权重和总长度,这是最常见的错误,直接导致大数据量测试用例运行错误; - 堆类型错误:误用默认大根堆,导致每次取出的是最大权重节点,合并逻辑完全错误,结果偏离正确值;
- 输入超时 :未添加输入加速代码,处理 2 × 10 5 2×10^5 2×105个数据时cin读取速度过慢,触发时间限制;
- 边界忽略 :额外添加 n = 1 n=1 n=1的判断逻辑(如
if(n==1) cout<<a[0]<<endl;),错误输出字符出现次数而非0。
题目4 设计LRU缓存结构
题目描述:
设计LRU(最近最少使用)缓存结构,该结构在构造时确定大小,假设大小为 capacity,操作次数是 n ,并有如下功能:
Solution(int capacity):以正整数作为容量 capacity 初始化LRU缓存get(key):如果关键字 key 存在于缓存中,则返回key对应的value,否则返回 -1。set(key, value):将记录(key,value)插入该结构,如果关键字 key 已经存在,则变更其数据值 value,如果不存在,则向缓存中插入该组 key-value ,如果key-value的数量超过 capacity,弹出最久未使用的key-value
提示
1.某个key的set或get操作一旦发生,则认为这个key的记录成了最常使用的,然后都会刷新缓存。
2.当缓存的大小超过capacity时,移除最不经常使用的记录。
3.返回的value都以字符串形式表达,如果是set,则会输出"null"来表示(不需要用户返回,系统会自动输出),方便观察。
4.函数set和get必须以O(1)的方式运行
5.为了方便区分缓存里key与value,下面说明的缓存里key用"#"号包裹
数据范围1 ≤ capacity ≤ 10⁵
0 ≤ key,val ≤ 2×10⁹
1 ≤ n ≤ 10⁵
输入
["set","set","get","set","get","set","get","get","get"],[[1,1],[2,2],[1],[3,3],[2],[4,4],[1],[3],[4]],2输出
["null","null","1","null","-1","null","-1","3","4"]说明
我们将缓存看成一个队列,最后一个参数为2代表capacity,所以:
Solution s = new Solution(2);
s.set(1,1); //将(1,1)插入缓存,缓存是{"1"=1},set操作返回"null"
s.set(2,2); //将(2,2)插入缓存,缓存是{"2"=2, "1"=1},set操作返回"null"
output=s.get(1);//因为get(1)操作,缓存更新,缓存是{"1"=1, "2"=2},get操作返回"1"
s.set(3,3); //将(3,3)插入缓存,缓存容量是2,故去掉末尾的key-value,缓存是{"3"=3, "1"=1},set操作返回"null"
output=s.get(2);//因为get(2)操作,不存在对应的key,故get操作返回"-1"
s.set(4,4); //将(4,4)插入缓存,缓存容量是2,故去掉末尾的key-value,缓存是{"4"=4, "3"=3},set操作返回"null"
output=s.get(1);//因为get(1)操作,不存在对应的key,故get操作返回"-1"
output=s.get(3);//因为get(3)操作,缓存更新,缓存是{"3"=3, "4"=4},get操作返回"3"
output=s.get(4);//因为get(4)操作,缓存更新,缓存是{"4"=4, "3"=3},get操作返回"4"