
◆ 博主名称: 小此方-CSDN博客
大家好,欢迎来到小此方的博客。
⭐️个人专栏:《C语言》_小此方的博客-CSDN博客
⭐️踏破千山志未空,拨开云雾见晴虹。 人生何必叹萧瑟,心在凌霄第一峰。
➤ 老规矩:先看题目
给你一个链表的头节点
head,判断链表中是否有环。如果链表中有某个节点,可以通过连续跟踪
next指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数pos来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:
pos不作为参数进行传递。仅仅是为了标识链表的实际情况。如果链表中存在环 ,则返回
true。 否则,返回false。
➤ 题目非常简单,我们用一个快慢指针的思路就可以解决。
objectivec
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
typedef struct ListNode listnode;
bool hasCycle(struct ListNode *head)
{
listnode*fast=head;
listnode*slow=head;
while(fast&&fast->next)
{
fast=fast->next->next;
slow=slow->next;
if(slow==fast)
{
return true;
}
}
return false;
}➤ 一图解释这个原理:(注意图中的结点间隔非真实间隔:即只做示意)
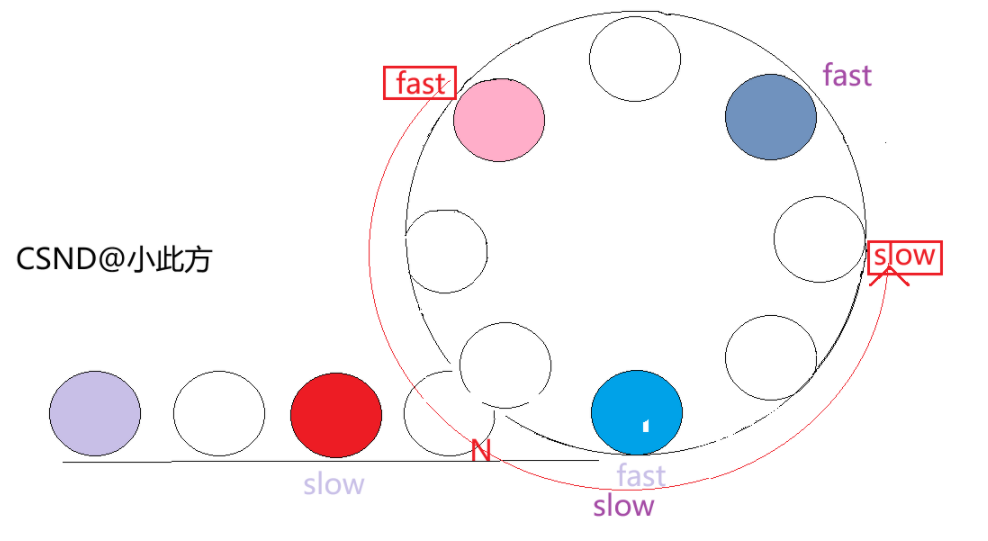
(如下:颜色对应图片)
✦ 1,slow指针和fast指针从链表头部(head)开始
✦ 2,fast一次走一步,slow一次走两步,此时fast指向【环的开始】
✦ 3,fast进入循环,slow随后指向【环的开始】
✦ 4,slow进入循环,此时,这个问题的性质变成了------------追击问题
✦ 5,我们假设fast到slow指针的距离是N,fast每次走两步,slow每次走一步,速度差为一步。
✦ 6,因此,每走一次,fast距离slow就缩短1,(N-1)直到最后,fast将会追上slow。
那么,这就结束了吗?远远没有。面试官一定会在次基础上问你更加深入的问题:
✦ 1,fast有咩有可能错过slow,永远也追不上?
✦ 2,如果fast一次走3步,4步,5步......x步呢?追上还是错过?
接下来就为大家解答第二个问题:(第一个问题在上面已经做出了解释)
➤当fast走x步
将这个问题简化,我们先来探讨:当fast走3步的时候。
fast和slow的速度差为3-1=2。此时,我们需要对slow进入循环时(即追及问题开始时),fast到slow的距离N进行讨论。
✦ N分别为奇数和偶数时
fast和slow移动时,N每次-2。我们画出这样一张表格:
| N为偶数 | N为奇数 |
|---|---|
| N | N |
| N-2 | N-2 |
| N-4 | N-4 |
| N-6 | N-6 |
| ............... | ............... |
| 6 | 5 |
| 4 | 3 |
| 2 | 1 |
| 0(追上) | -1(错过) |
可见,当N为奇数时,最终N=-1;会错过slow指针。而N为偶数时,刚好会追上slow指针。
那么问题又出现了:fast在第一轮错过了slow,在第二轮及以后会永远错过还是可能追上?
此时:我们不得不引入一个新的变量:C(circle)表示整个环的长度。
于是我们可以定义:当N=-1时(事实上就是去掉当前fast这个结点外的长度)fast到slow的长度为C-1;
接下来我们继续对C-1的奇偶讨论:
| C-1是偶数 | C-1是奇数 |
|---|---|
| C-1 | C-1 |
| C-3 | C3 |
| C-5 | C-5 |
| C-7 | C-7 |
| ............... | ............... |
| 6 | 5 |
| 4 | 3 |
| 2 | 1 |
| 0 | -1 |
✦ 显然,当C-1为偶数时在第二次追击时能够追上。
✦ 当C-1为奇数时,第二次及以后无数次永远不可能追上。
➤总结
回到刚才的问题:
2,如果fast一次走3步,4步,5步......x步呢?追上还是错过?
实际上,一切的关键在于三点:速度差(我们暂时用一个字母V表示),起始间距N,以及环总长C
➧ 如果起始间距是速度差的倍数,即:N%V==0,那么第一轮追击就可以追到。
➧ 如果起始间距不是速度差的倍数,即N%V!=0,那么第一轮追击就不可能追上。
✦如果C-(错过的步数x)是N的倍数,那么在第n(n>=2)轮就会追上。
✦如果C-(错过的步数x)不是N的倍数,那么永远也追不上。
➤真的永远也追不上吗?
有些小伙伴可能尝试着去用代码验证了一边上面的结论:发现,出现问题了。所以,结论问题出在哪里?就以fast的速度是slow的三倍的情况为例:
结论:
➧ 如果起始间距N是偶数,那么第一轮追击就可以追到。
➧ 如果起始间距N是奇数,那么第一轮追击就不能追到。
✦如果C-1是偶数,那么在下一轮就会追上。
✦如果C-1是奇数,那么永远也不能追不上。
既然"永远也不会追上 "的条件不成立,那么反推**"C是偶数并且N为奇数"**的条件也不成立
重新回到这个图:
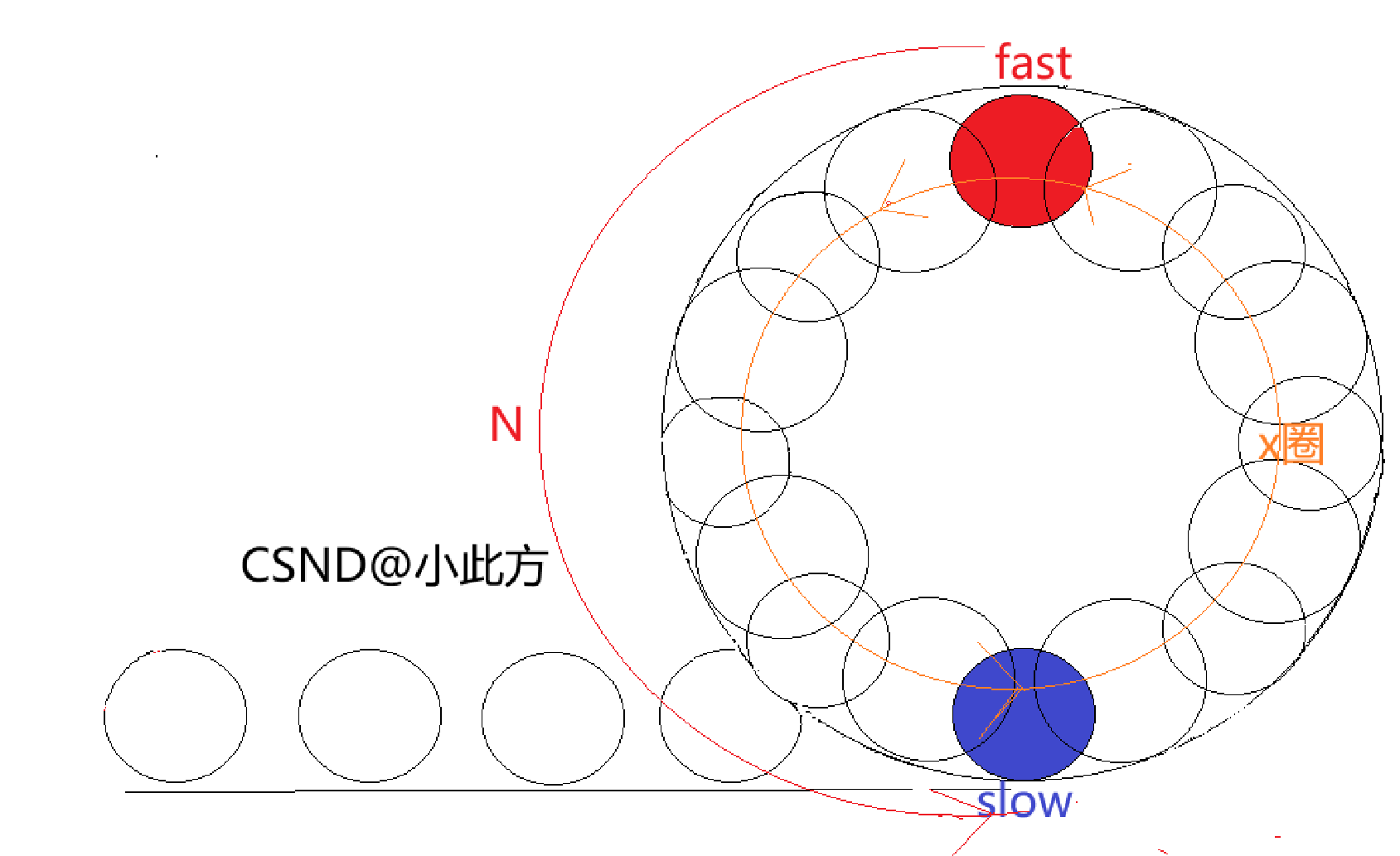
在此之前,我们忽略了一个细节:当slow准备进入循环时,fast可能已经走了很多圈了。
我们把圈数记为x,fast的速度是slow的三倍,所以速度差是两倍。
✦设进入循环后,slow的路程为L,fast的路程为3L
✦fast的路程可以表示为:3L=x*C+C-N。
✦slow的路程可以表示为:L
✦3L-L=2L=x*C+C-N=(x+1)*C-N
此时,我们在再C是偶数并且N为奇数的条件带进去:发生了矛盾。
由此证明了:这种情况下:不可能发生"永远也追不上的情况"。
好的,这个问题的讨论就到这里,我是此方,我们下期再见。