问题
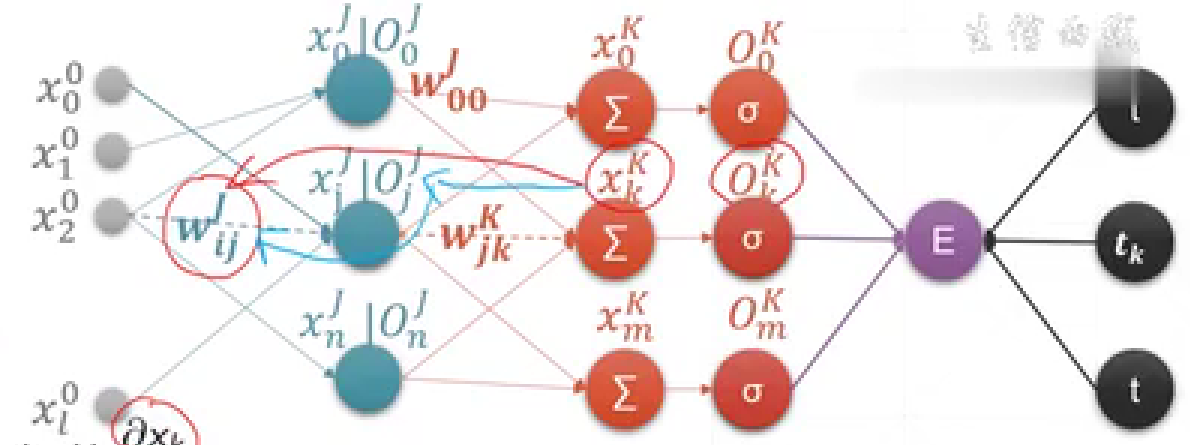
在学习反向传播的过程中,对于如下这一步:

我有了些问题,可以在上图中看到,xk和Oj之间还有一个wjk,而xk是等于求和Ojwjk这些的。那么我想,是否可以把dxk/dOj变为dxk/dwjk * dwjk/dOj(为方便没用δ)?由此,我开始了思考。
思考
要解决这个问题,首先就要知道,常数能不能作为导数?因为我们知道wjk大概是个常数。先来看一个例子:
想象一下,最简单的函数:y = 2 * x,我们都知道,y 对 x 的导数是2,什么意思呢?就是当 x 移动 1个单位的时候,y 移动两个单位。
那么,
y对2可不可以求导呢?我想(开始猜想,如有不对,恳请指正!)答案是可以,那么2移动一个单位的时候,y如何变化?答案是没有变化。因为y = 2x是一个图像对吧,是一个经过坐标轴原点的倾斜的直线。那么2如果进行变化了(hhh常数感觉就不应该变化,不过我也搞不懂说实话,猜就完事了,尽情幻想)和x没有关系那么x既然没有发生变动,那么y变了嘛?显然没有。
那么,
2变化一个单位,比如说2变成3了,但是y没有变化,也就是dy=0.
显然,
y对2的导数,是0。
好了,经过我们的思考过后,发现,y对常数可以求导,只不过是0。
回到我们最初的问题,dxk/dOj变为dxk/dwjk * dwjk/dOj,那么我们说,既然可以对常数求导,那么当然也可以对wjk求导(这里隐含了一个假设,wjk是常数,我们之后会分析这一点,暂且随我向前)。
那么我们对wjk求导可知,这个结果是0,但是后面还有一块,常数对变量求导,这个东西又是很奇怪。那么我们不得不再进行考虑。
突然,想到一点,我们为什么想把左边(dxk/dOj)变为右边(dxk/dwjk * dwjk/dOj)?
实际上除了对常数求导的迷思解决了以外,这里还有一个假设,就是我们可以进行链式求导,那么不妨我们深入一下链式求导:
上面是维基百科对于链式法则的解释,可以看到,链式法则是需要g对y可微分以及y对x可微分。也就是说,链式法则的成立需要中间变量非独立,常数显然不可以。
因此,我们无法用链式法则用常数作为中间变量对g进行求导。
那么回到我们的初始问题:能否dxk/dOj变为dxk/dwjk * dwjk/dOj,答案显然是不行。
然而,这些一切都是基于wjk是常数的考量下的,然而,这里出现了第二个问题。
问题

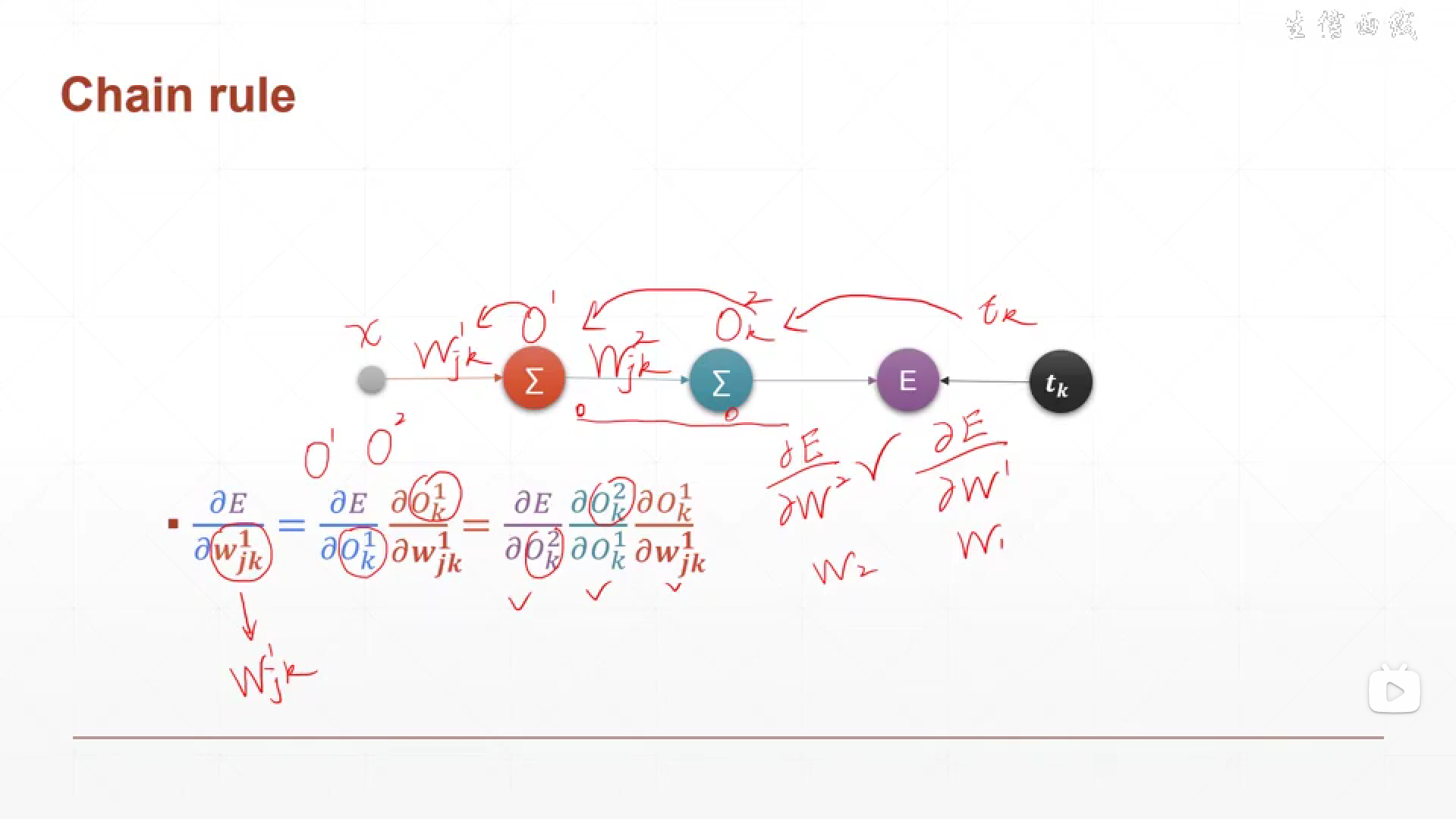
虽然说,我们知道了链式法则不能像我们之前提到的那样使用,但是,看到我们目前的图片,让我毛骨悚然的一点是,看看这个:dE/dwjk,这是什么?这不正是我们之前说的那个"常数"吗?
我们在深入链式法则中中间层的w的时候,却忘了在最开始,w就已经作为自变量,出现在我们面前了。
于是新的问题产生了,w,究竟是常数?还是什么???
思考
首先,我们看dE/dwjk,对于这个w,假如,他是常数,那么显然我们没必要求他,因为对常数求导,导数是0。那么所以说,这个w,他是一个自变量。在这个情况中,他就像y = 2x中的x一样。我们来画个草图:
他是这样的一个感觉。
那么,在这种情况下,他是一个自变量,那么为什么在刚才的情况下,我们不能够作为链式法则使用呢?
我想,这是因为w的角色不同。
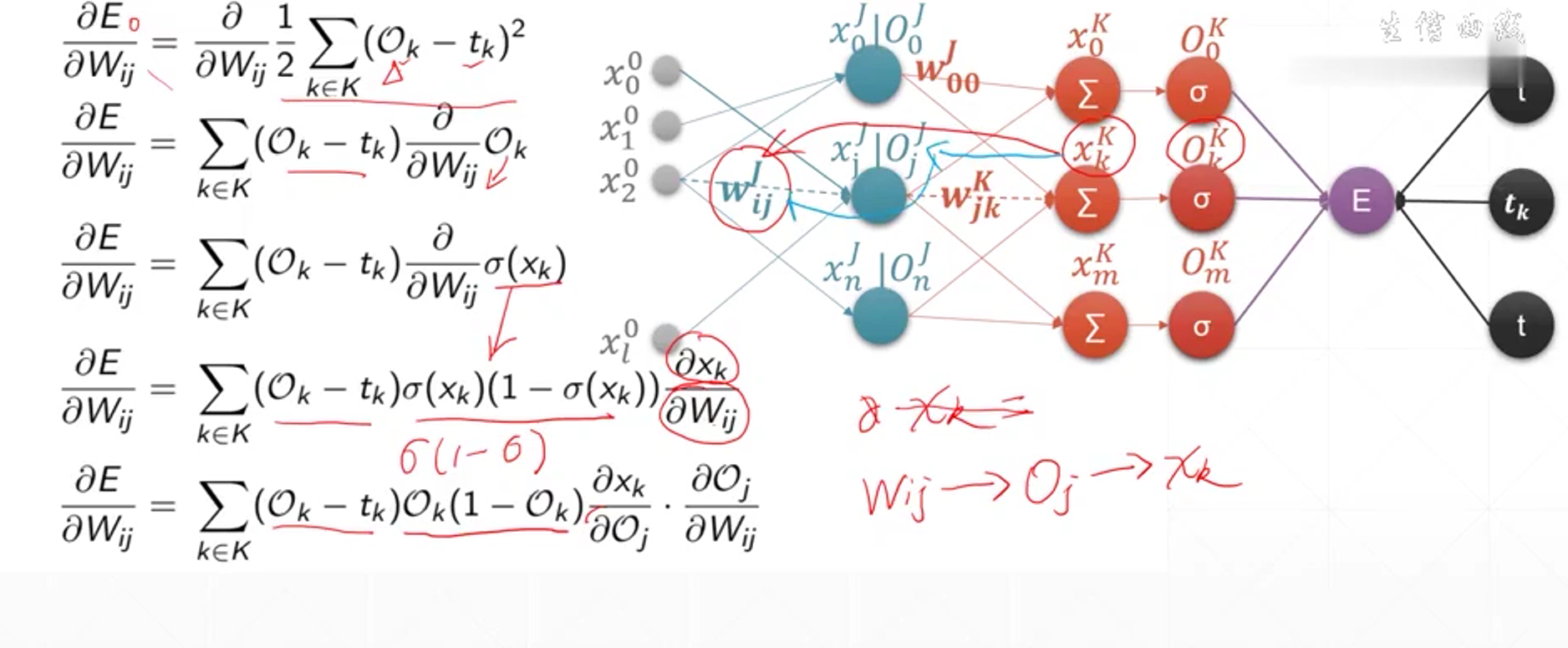
就像上图中,在dE/dwij的情况下,由于E是关于wij的函数,就是我现在就是要求wij变化的时候,E怎么变,那么自然,我是可以让wij作为自变量的。
然而,在如下这个部分,我们不可以拆分:
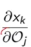
虽然中间有一个wjk,但是我们现在更新的是wij,我认为,神经网络的参数应该是逐层更新 的,那么,wjk 在这个场景下,就应该是一个常数 。原因就是逐层更新,而现在没有更新他 。那么我想他的值就是之前前向传播来的值,且固定。
至此,完成了我们这两个问题的辨析。
总结
总的来说,这个w究竟是常数还是自变量,要看这个w是否是现在正在更新,如果只是中间的一个参数,那么就把他视作常数。但是,如果他正在更新,那么就要把他视作自变量,因为我们要对他进行更新。
楼主机器学习小白,如有不对,还望各位不吝指正!
参考资料
【1】龙良曲PyTorch入门到实战(附课程源码)全150讲,绝对通俗易懂!_AI人工智能/计算机视觉/深度学习/pytorch/神经网络
