目录
[1. 基本概念](#1. 基本概念)
[2. 序贯覆盖](#2. 序贯覆盖)
[3. 剪枝优化](#3. 剪枝优化)
[3.1 预剪枝：早停指标](#3.1 预剪枝：早停指标)
[3.2 后剪枝 -- REP \ IREP \ IREP* \ RIPPER](#3.2 后剪枝 -- REP \ IREP \ IREP* \ RIPPER)
[4. 一阶规则学习](#4. 一阶规则学习)
[5. 归纳逻辑程序设计 ILP](#5. 归纳逻辑程序设计 ILP)
[5.1 最小一般泛化 LGG](#5.1 最小一般泛化 LGG)
[5.2 逆归结](#5.2 逆归结)
1. 基本概念
"规则学习" （rule learning）是从训练数据中学习出一组 能用于对未见示例进行判别的规则。
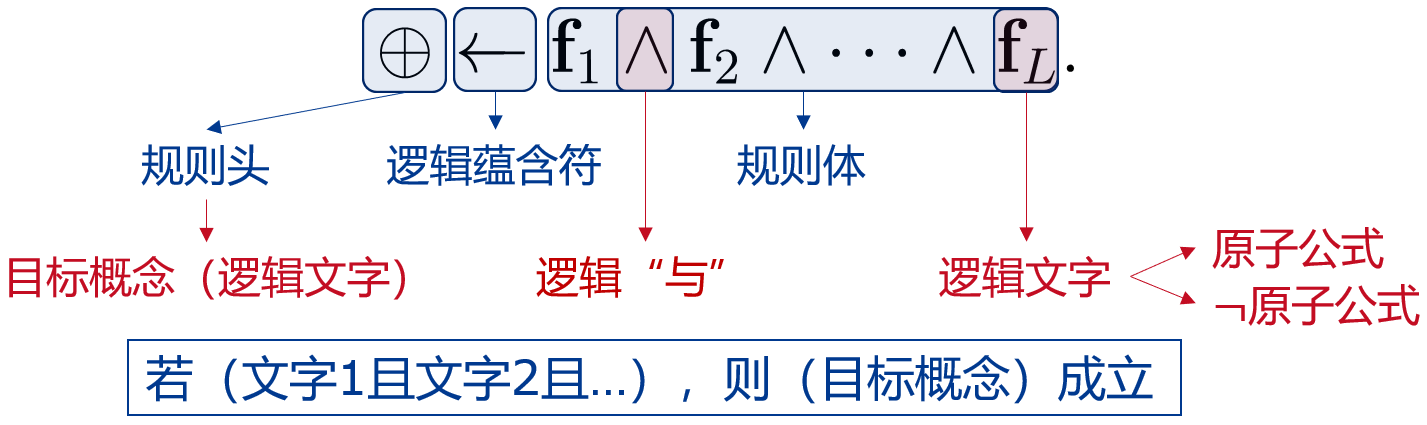
数理逻辑简洁地刻画和表达，例如 "父亲的父亲是爷爷" 这样的知识不易用函数式描述，
而用一阶逻辑则可方便地写为 "爷爷(X,Y) ← 父亲 (X,Z) ∧ 父亲(Z,Y)"
比如下面两条定义什么可以推出是好瓜 or 不是好瓜：
- 规则 1: 好瓜 ← (根蒂 = 蜷缩) ∧ (脐部 = 凹陷)；
- 规则 2: ¬ 好瓜 ← (纹理 = 模糊) ．
符合该规则的样本 称为被该规则 "覆盖"。
规则集合中的每条规则都可看作一个子模型 ，规则集合是这些子模型的一个集成。
当同一个示例被判别结果不同的多条规则覆盖 时，称发生了**"冲突"，**
需要进行 "冲突消解"：
投票法、排序法（按照排在前面的规则）、"元规则法"（定义规则如何使用的规则）
逻辑连接词（与、或、非、蕴含）
命题规则 or 一阶规则：由【原子命题 or 原子公式】和 逻辑连接词 构成的简单陈述句。
若规定 "自然数(X)" 表示 X 是自然数，σ(X) = X+1；
那么"所有自然数加1 都是自然数" 可写为，
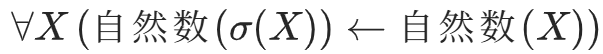
2. 序贯覆盖
规则学习的目标：产生一个能覆盖尽可能多的样例的规则集。
"序贯覆盖"：在训练集上每学到一条规则，就将该规则覆盖的训练样例去除，继续学。
产生一条规则就是寻找最优的一组逻辑文字来构成规则体，这是一个搜索问题。
自底向上（特殊到一半）：从单个样本，删除文字扩大规则覆盖范围。（适合少样本）
自顶向下（一般到特殊）：从比较一般的规则，添加文字缩小覆盖范围。（泛化性更好、噪声鲁棒性）
先加一个规则，覆盖正例 / 覆盖总数 = 准确率，每轮准确率最高的，
再进入下一轮加下一条规则，直到覆盖都是正例。
搜索过程贪心，容易局部最优 -> 可用 beam search 束搜索。
（每轮就选准确率前 k 高的组合）
规则生成过程中涉及一个评估规则优劣的标准：
可以用 （规则准确率、信息增益率、覆盖样例数、属性次序）等等。
3. 剪枝优化
贪心搜索 过拟合 / 没得到全局最优解。（类似决策树 需要剪枝）
3.1 预剪枝：早停指标
如 CN2 算法设置，LRS 比较大停止继续向下搜索规则。
似然率统计量 Likelihood Ratio Statistics LRS：
衡量了规则（集）覆盖 样例的分布 与 训练集经验分布的差别。
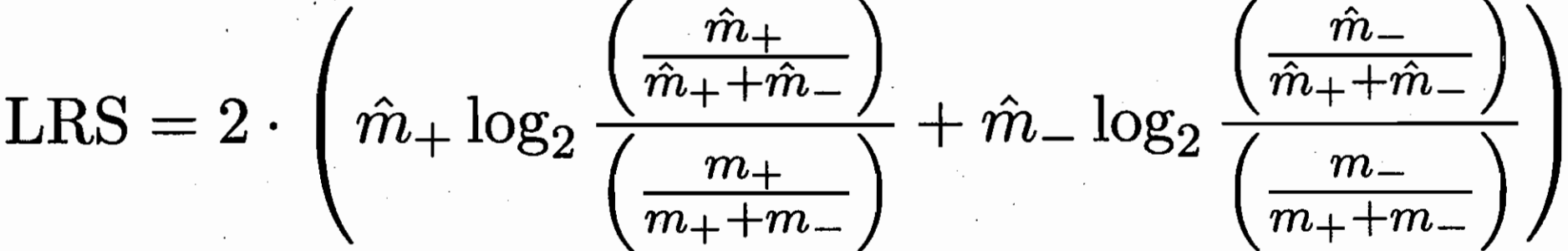
LRS 越大，用 "规则集预测" 相比于按照 "原正反例比例猜测" 效果越好。
3.2 后剪枝 -- REP \ IREP \ IREP* \ RIPPER
"Reduced Error Pruning" 减错剪枝 REP
从训练集 上学得规则集 R 后进行多轮剪枝，穷举所有剪枝操作，
再在验证集评估 所有候选规则集，保留最好的进下一轮剪枝。（但是穷举复杂度太高）
I（Incremental）REP
相比 REP 生成完规则后再进行后剪枝；IREP 每生成一条规则后都剪枝一下。（时间复杂度降低）
IREP* ：评判指标替换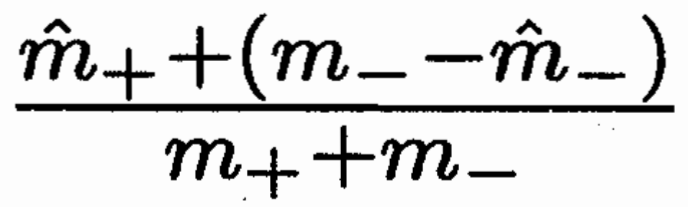 
取代了之前的准确率。
分母是当前集合总样本数，
分子为 规则覆盖的正例 + 未被规则覆盖的负例（乐观的认为他们后面会被判为正例）。
好处：原来的 "正确率" 负例太敏感，即使覆盖了很多正例，包含一些负例惩罚力度太大。
减少了 "过度剪枝"，并且全局视野，把剩下的样本交给后面的规则做。
IREP的问题：剪枝后，将这条规则覆盖的实例 从训练集中移除。
这种 "立即移除" 的策略使得算法对数据分割的顺序 非常敏感，容易陷入局部最优。
RIPPER：对规则集 R 中的每条规则 ri，产生两个变体。
替换规则 r1：基于 ri 覆盖的样例，用 IREP* 重新生成 r1。
修订规则 r2：ri 增加文字进行特化，用 IREP* 剪枝生成 r2。
比较原始的 R 和 （用r1换r后的 R' ）（用r2换r后的 R'' ）；保留三者中的最优。
4. 一阶规则学习
关系信息很重要，比如挑西瓜，我们不知道多绿才算"色泽青绿"，
我们会将西瓜进行相互比较，例如，"瓜 1 的颜色比瓜2 更深"
也会得到，X 和 Y 满足 *** 比较条件则，X 比 Y 更好 / 更差。
FOIL（First-Order Inductive Learner）
与命题规则学习类似，满足 更好(X,Y) 的为一阶规则覆盖的正例。
增加文字时，类似序贯覆盖，指标使用 FOIL 增益。
F_Gain = 新规则覆盖的正例数 * 新旧规则正例比例差异
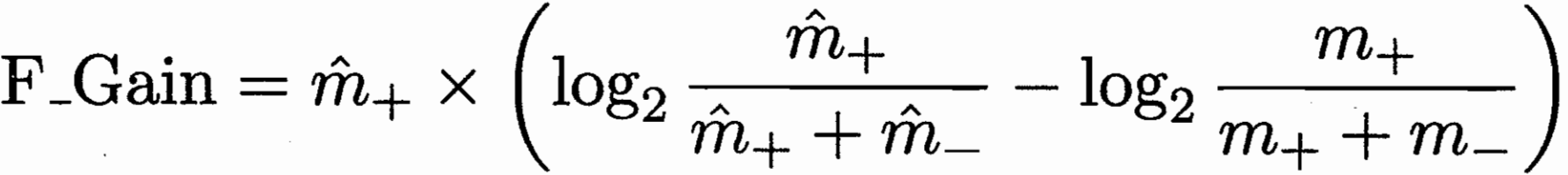
5. 归纳逻辑程序设计 ILP
归纳逻辑程序设计 (Inductive Logic Programming)
在一阶规则学习中引入了函数和逻辑表达式嵌套。
自底向上 ，从特殊泛化到一般。
5.1 最小一般泛化 LGG
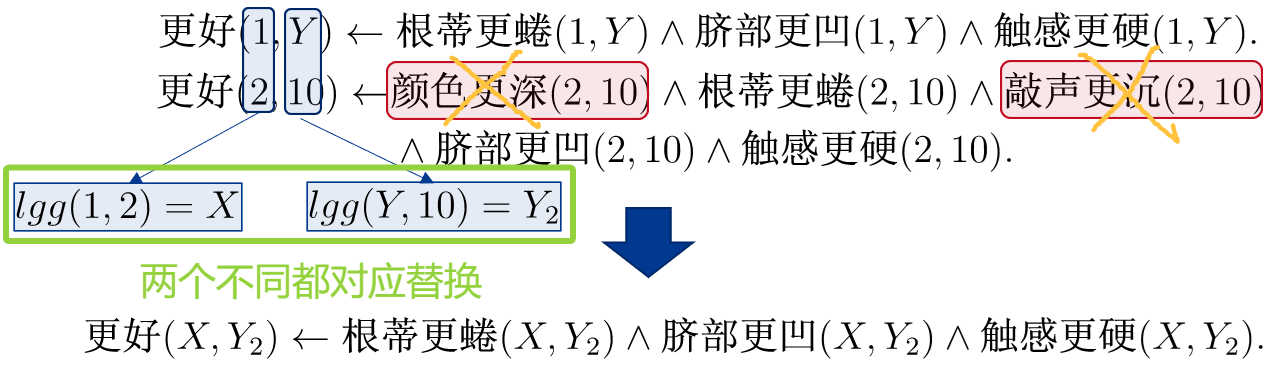
寻找两条规则的 LGG：
因为两个都是 1，一个是 10 一个是 15，把 10 和 15 都换成 Y。
并且 "声音更沉" 这个谓词不是交集，所以删除。
同理，如果再加一条规则；对应比较的两个都不同，都替换。
5.2 逆归结
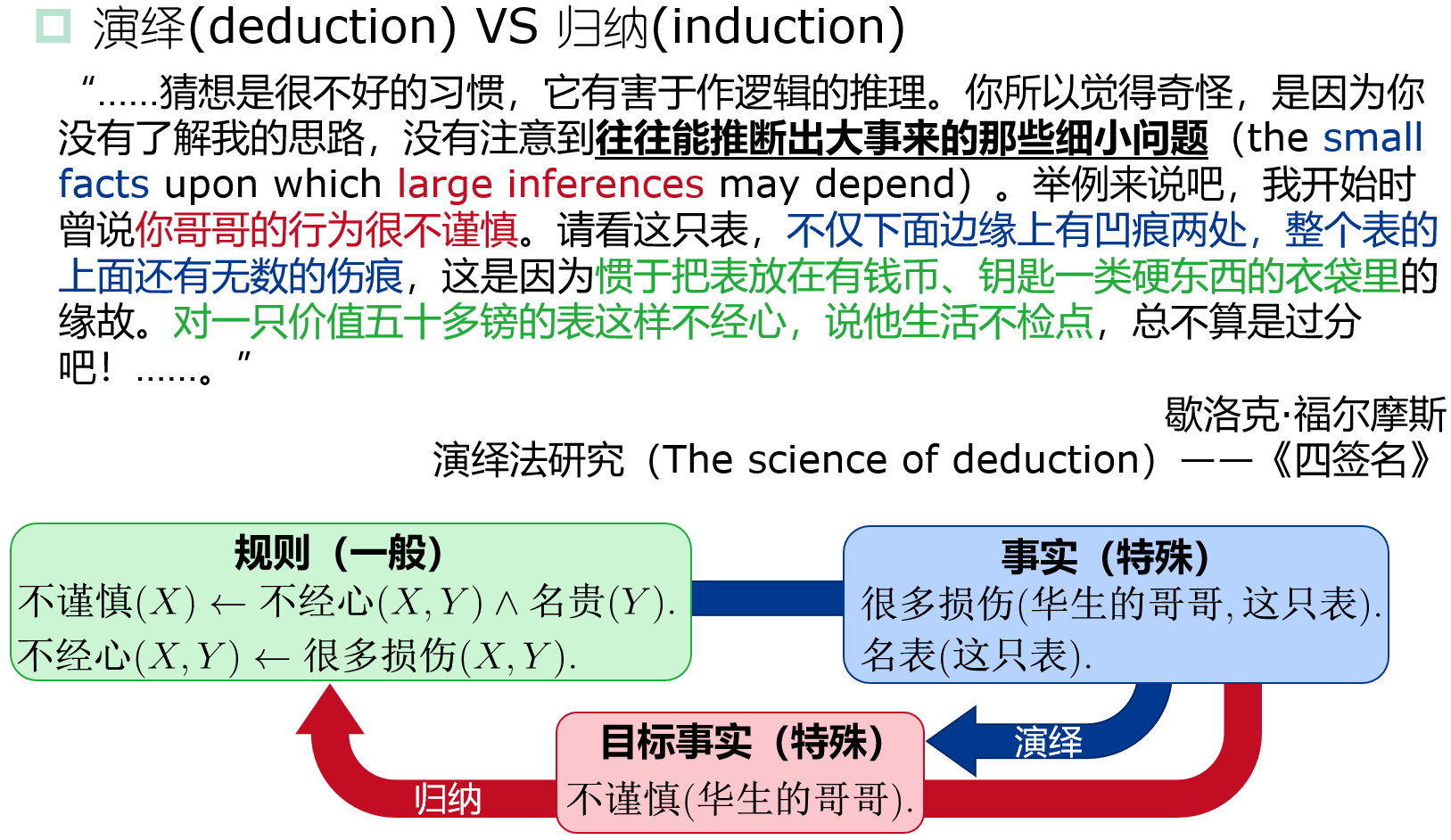
归纳：特殊到一般； 演绎：一般到特殊。
很多损伤 -> 人对表不经心； 表名贵 + 人对表不经心 -> 人不谨慎
可对应真值表。
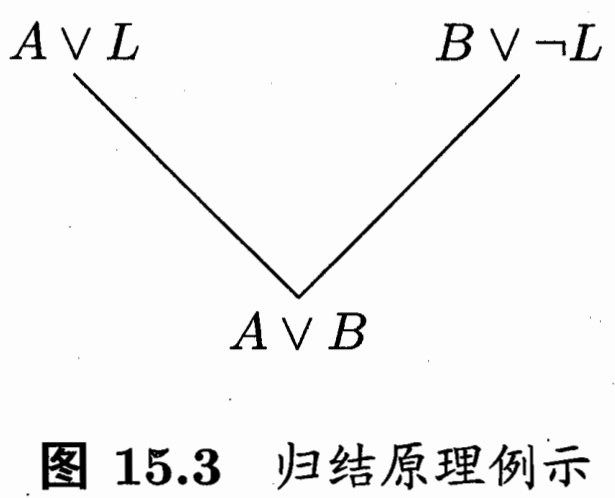
四种完备的逆归结操作；上面的可推出下面。
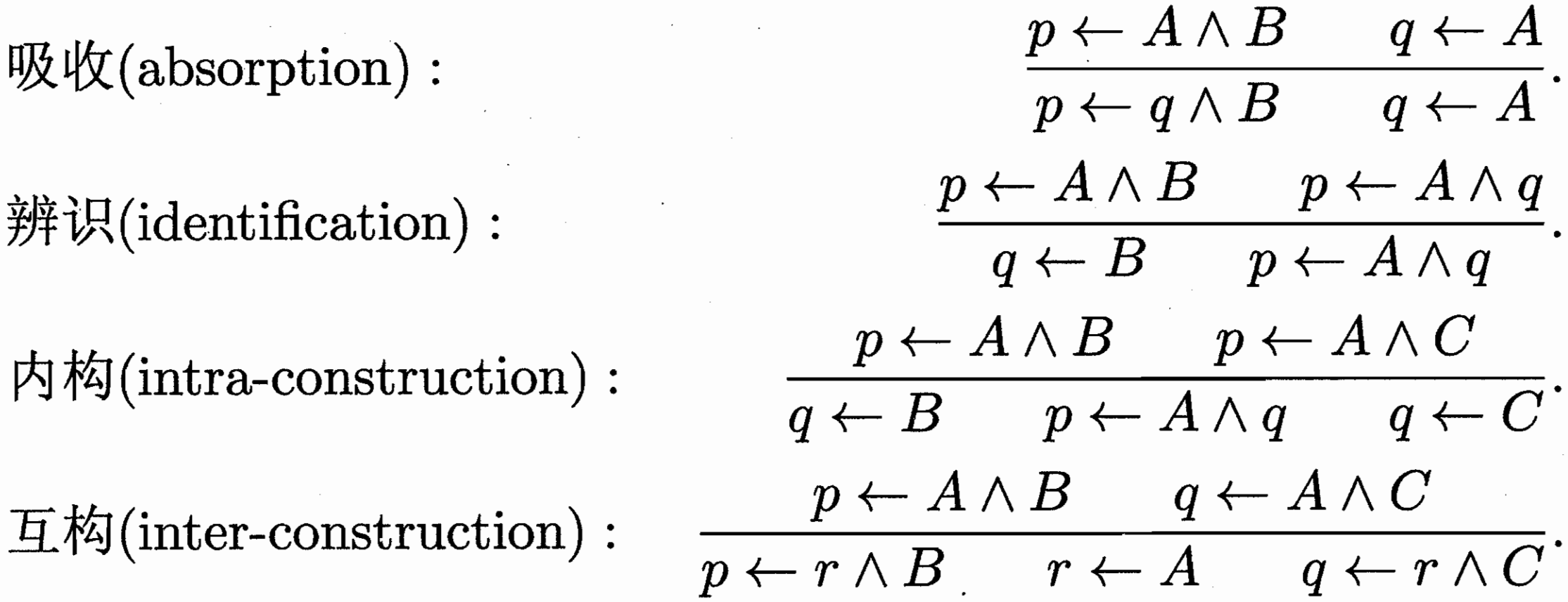
Prolog 示例，描述家庭成员关系；
由父母，性别；进一步定义什么是 祖父母，女儿等等。
