Zset
Zset是有序集合
注意:此处的有序就不是list和set的有序无序的有序了,list的有序是顺序有影响,set是无序的表示顺序不影响,而这里的有序指的是升序/降序的有序。
set:1、唯一 2、无序
孙行者,行者孙,者行孙 =》同一只猴
list:1、有序的 2、不唯一
孙行者,行者孙,者行孙 =》不同的猴
那这里排序的规则是什么呢?
redis给zset中的member同时引入了一个属性:分数,浮点类型。每个member都会安排一个分数。进行排序的时候就会依照此处的分数大小来进行升序/降序的排序
Zset中的member仍然要求是唯一的(score可以重复!!!)

命令
zadd
使用zadd向有序集合中,添加元素和分数。
ZADD key [NX | XX] [GT | LT] [CH] [INCR] score member [score member
...]ps:score,分数;member,元素。添加的时候,既要添加元素,又要添加分数。
不要把这里的member和score理解成"键值对",键值对中是有明确的"角色区分",谁是键,谁是值,是明确的,一定是根据键来查找值。
而对于有序集合来说是可以通过member来找到对应的score的,又可以通过score来找到对应的member。
时间复杂度:O(logN)
由于zset是有序的,要求新增的元素,要放到合适的位置上~~(找位置)
当然,时间复杂度是logN而不是N,也是充分地利用了有序这样的特点~~(zset的内部结构主要是跳表)
返回值:本次添加成功的元素个数。
zadd详解
NX|XX:

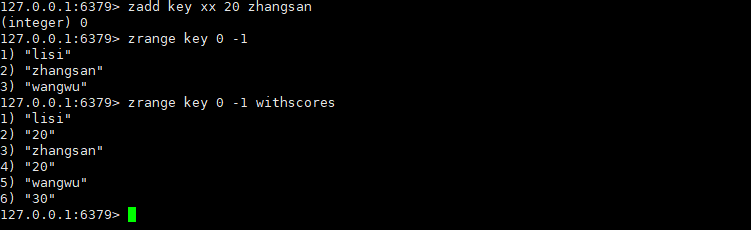
LT|GT

这里的LT|GT是redis6新增的,博主的redis版本只有5,因此无法进行演示。
CH

更新2+新增1 = 3
incr
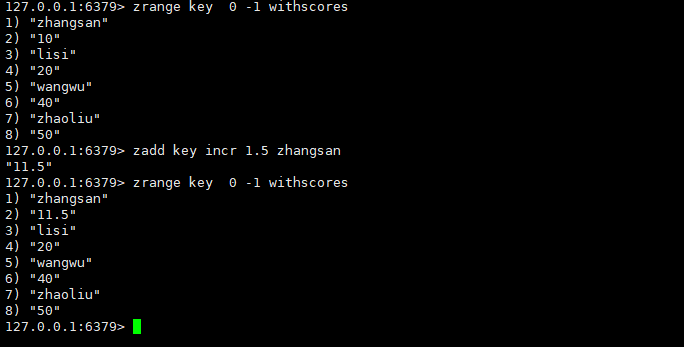
之前我们讲到zset会根据member的score进行排序,那如果member的score相同又会发生什么情况呢?
可以看到,分数相同,就会根据当前元素的字典序来排列;分数不同则仍按分数升序排序。
zrange
使用zrange就可以查看zset中的元素详情了~~
类似于lrange,可以指定一对下标构成的区间。有序集合,本身元素就是有先后顺序的~~谁在前,谁在后,都是很明确的!!因此也就可以给这个有序集合赋予下标这样的概念了~
ZRANGE key start stop [WITHSCORES]时间复杂度:O(log(N)+M),N为有序集合内元素个数,M为区间内元素个数。(此处要先根据下标找到边界值,找到之后就需要遍历了)
返回值:区间内的元素列表
zcard
获取一个zset的基数,即zset中的元素个数。
ZCARD key时间复杂度:O(1)
返回值:zset内的元素个数。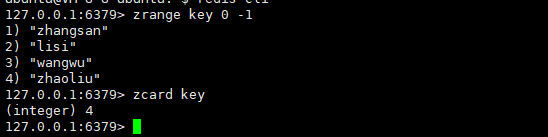
zcount
返回分数在min和max之间的元素个数,默认情况下,min和max都是包含的(闭区间),可以通过 "(" 进行排除。
ZCOUNT key min max时间复杂度:O(log(N))
返回值:满足条件的元素列表个数
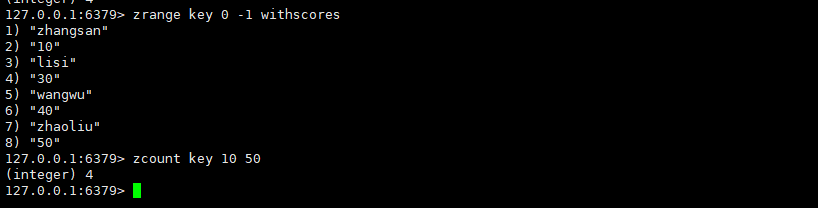
可以通过"("来排除区间边界元素
注意:这里zcount指定min和max分数区间,并不是根据min找到对应的元素,再根据max找到对应的元素。实际上,Zset的内部,会记录每个元素当前的"排行"/"次序"。查询到元素,就直接知道了元素所在的"次序"(下标),就可以直接把max对应的元素次序和min对应的元素次序,作减法即可!!
min和max是可以写成浮点数的:
再浮点数中,存在两个特殊的数值:
inf:无穷大
-inf:负无穷大 注意:负无穷大并不是无穷小

zrevrange
返回指定区间的元素,分数按照降序排序。带上withscores可以把分数也返回。(rev:reverse =》逆序)
时间复杂度:O(log(N)+M)
返回值:区间内的元素列表。
zrangebyscore
按照分数来找元素的,相当于和刚才的zcount类似。
备注:这个命令可能在6.20之后废弃,功能合并到zrange
ZRANGEBYSCORE key min max [WITHSCORES]时间复杂度:O(log(N)+M)
返回值:区间内的元素列表。
zpopmax
删除并返回分数最高的count个元素。
ZPOPMAX key [count]时间复杂度:O(log(N)*M)(N是有序集合元素的个数;M是count,即要删除的元素个数)
返回值:分数和元素列表。
如果当前有序集合中存在两个相同score的元素,再进行删除会怎么样呢?
结论:如果存在多个元素,分数相同,同时为最大值,popmax删除仍然只删除其中一个元素(分数虽然是主要因素,如果分数相同则会按照member的字典序进行排序)
此处删除的是最大值,相当于尾删。既然是尾删,为什么我们不把这个最后一个元素的位置特殊记录下来~~后续删除不就可以O(1)了吗?省去了查找的过程~~
这是可以做到的,但是redis并没有这么做,事实上,redis的源码中,针对有序集合确实是记录了尾部这样特定位置~~但是在实际删除的时候,并没有用上这个特性,而是直接调用了一个"通用的删除函数"
此处是存在优化空间的,但是未来会进行优化这件事是不好说的,因为当前这个logN的速度其实是不慢的,如果N不是非常大基本上是可以看做O(1)的。
优化这种活要优化到刀刃上~~优化一般是要先找到性能瓶颈,再针对性地优化!!!
bzpopmax
zpopmax的阻塞版本。
咱们这里的有序集合也可以视为是一个"优先级队列",有时候也需要一个带阻塞功能的"优先级队列"。
BZPOPMAX key [key ...] timeoutps:key:有序集合 timeout:表示超时时间,最多阻塞多久~~
bzpop是可以同时多个有序集合的
时间复杂度:O(logN)
返回值:元素列表

那如果当前bzpopmax同时监听了多个key,假设key是M个,此时时间复杂度是O(log(N)*M)吗?
不,这个操作并不是每个key都进行删除,而只删除第一个添加元素的key
zpopmin
删除并返回分数最低的count的元素。
ZPOPMIN key [count]时间复杂度:O(log(N)*M)
返回值:分数和元素列表。
此处的zpopmin和上面的zpopmax的逻辑是一致的(同一个函数实现的),虽然redis的有序集合也记录了开头的元素,但是删除的时候仍然使用的是通用的删除函数,导致出现了重新查找的过程~~
bzpopmin
zpopmin的阻塞版本。
BZPOPMIN key [key ...] timeout时间复杂度:O(logN)
返回值:元素列表。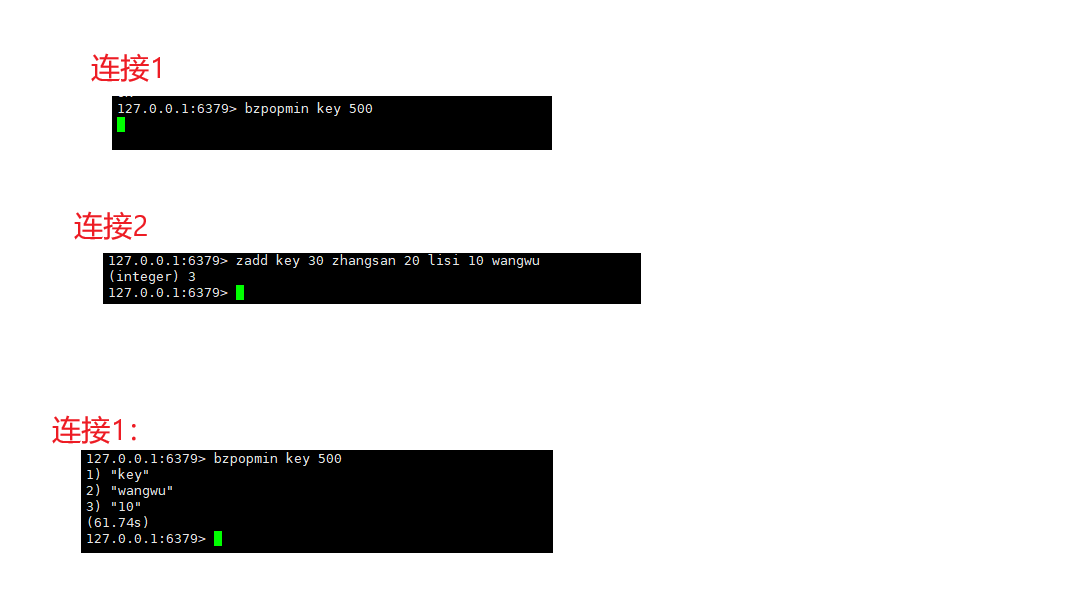
zrank
返回指定元素的排名,升序。
ZRANK key member时间复杂度:O(log(N))
返回值:元素列表
这里的时间复杂度和zcount一致,zcount也是先根据分数找到元素,再根据元素获取到排名,再把排名一减,得到了元素个数。
zrank得到的下标是,从前往后算的(升序)。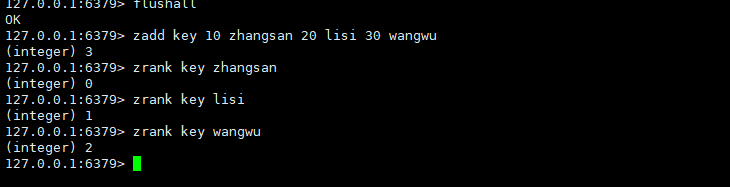
zrerank
返回指定元素的排名,降序。
ZREVRANK key member时间复杂度:O(log(N))
返回值:排名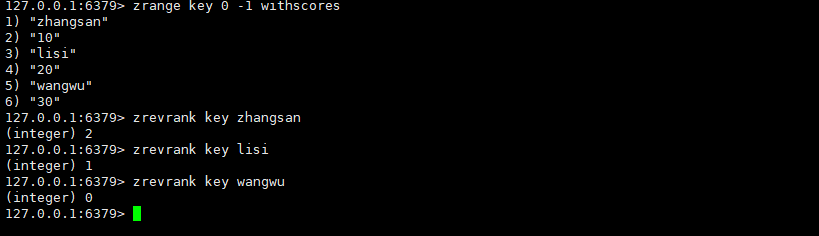
zscore
返回指定元素的分数
ZSCORE key member时间复杂度:O(1)
返回值:分数。
咦?前面,根据member找元素都是logN,这里不是也需要找元素吗?
此处相当于redis对于这样的查询操作做了特殊优化~~付出了额外空间代价~~针对这里优化到了O(1)实现。
zrem
删除指定的元素。
ZREM key member [member ...]时间复杂度:O(M*log(N)),N是整个有序集合的元素个数,M是参数中member的个数。
返回值:本次操作删除的元素个数。
zremrangebyrank
按照排序,升序删除指定范围的元素,闭区间。
ZREMRANGEBYRANK key start stop时间复杂度:O(log(N)+M),N是整个有序集合的元素个数,M是start-stop区间中的元素个数。此处查找元素位置,只需要进行一次(和zcount相同)。
返回值:本次操作删除的元素个数。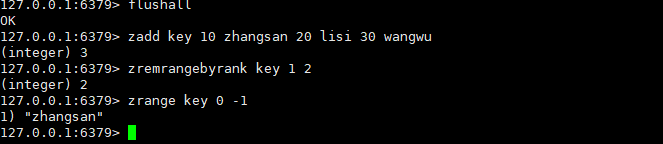
zremrangebyscore
按照分数删除指定范围的元素(闭区间)。
ZREMRANGEBYSCORE key min max时间复杂度:O(log(N)+M)
返回值:本次操作删除的元素个数。

zincrby
为指定的元素的关联分数添加指定的分数值。
ZINCRBY key increment member时间复杂度:O(log(N)) 此处不仅会修改分数内容,同时也能移动元素位置,保持整个有序集合仍然是升序的。
返回值:增加后元素的分数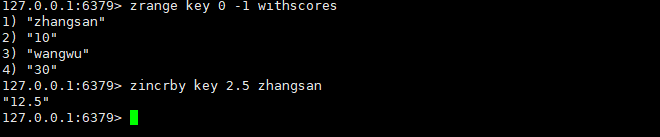
集合间操作
我们在set中已经学习了siner(集合间求交集)、sunion(集合间求并集)、sdiff(集合间求差集)。
但是ziner、zunion、zdiff是redis6.2版本才开始支持的,此处暂时无法演示。
zinerstore
将集合求交集并存储到另一个指定destination中。
ZINTERSTORE destination numkeys key [key ...] [WEIGHTS weight
[weight ...]] [AGGREGATE <SUM | MIN | MAX>]
时间复杂度:O(N*K)+O(M*log(M))N是输入的有序集合中,最小的有序集合的元素个数,K是输入了几个有序集合;M是最终结果的有序集合的元素个数。
返回值:目标集合中的元素个数。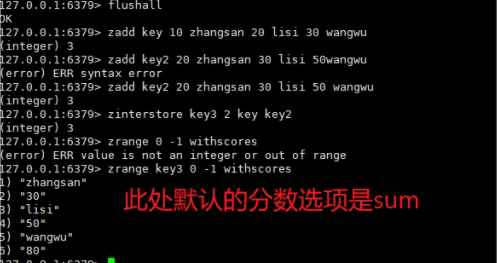
权重演示:
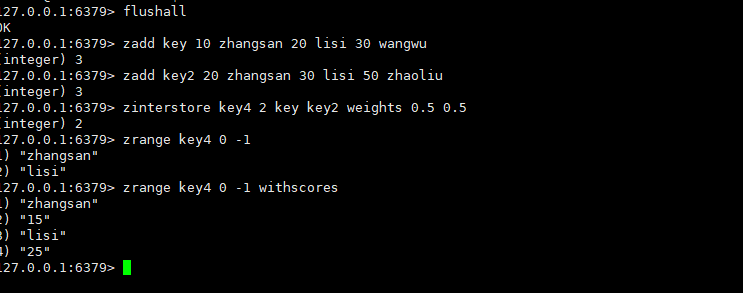
zhangsan scores:10*0.5+20*0.5 = 30
lisi scores:20*0.5+30*0.5 = 25
min: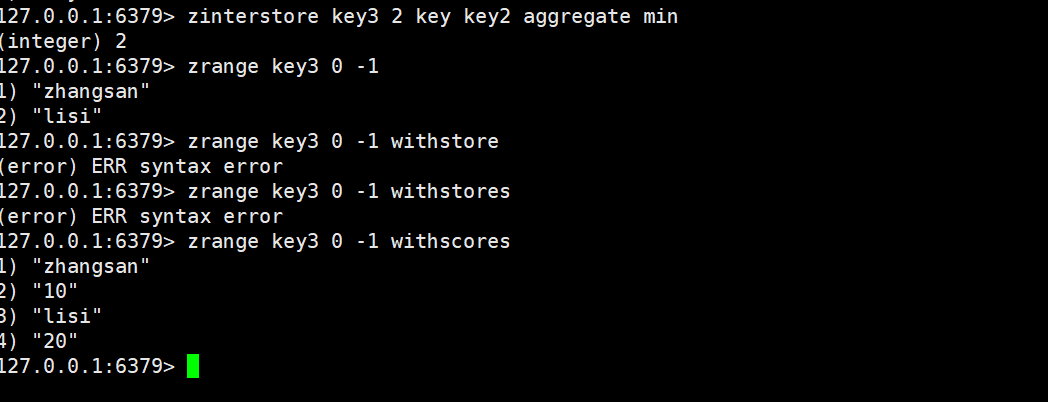
max:
zunionstore
将集合求并集并存储到另一个指定destination中。
ZUNIONSTORE destination numkeys key [key ...] [WEIGHTS weight
[weight ...]] [AGGREGATE <SUM | MIN | MAX>]时间复杂度:O(N*K)+O(M*log(M))N是输入的有序集合中,最小的有序集合的元素个数,K是输入了几个有序集合;M是最终结果的有序集合的元素个数。
返回值:目标集合中的元素个数。
用法基本与zinterstore一致,这里就不做过多赘述。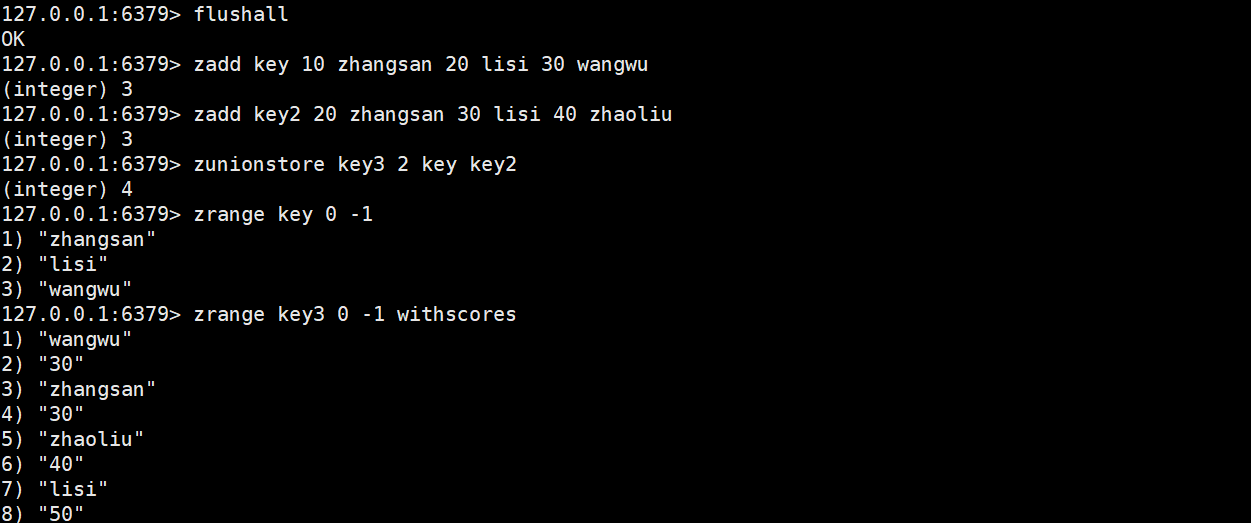
权重: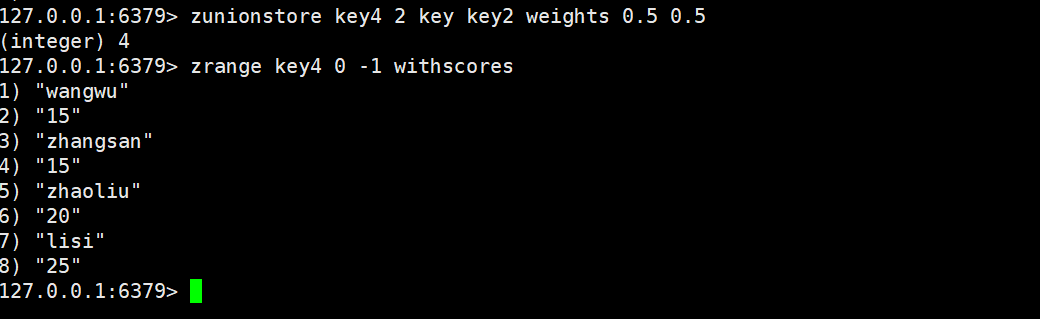
min:
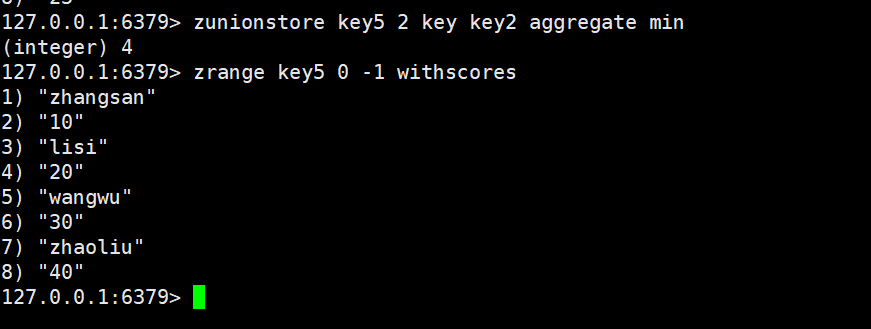
max: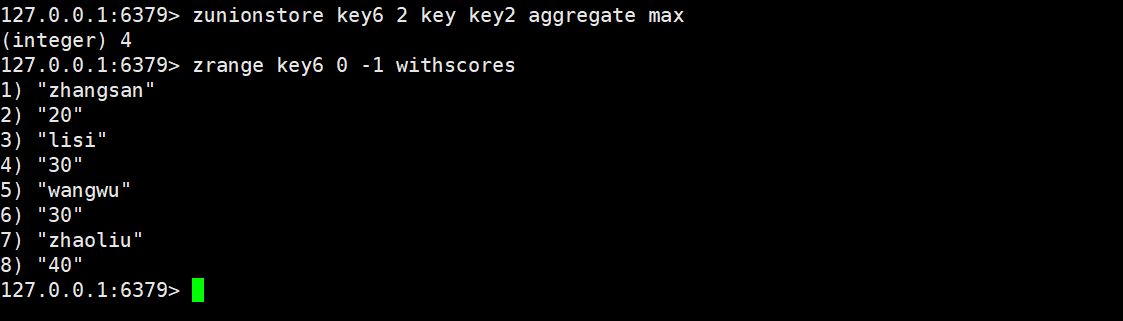
zdiffstore
将集合求差集并存储到另一个指定destination中。
ZDIFFSTORE destination numkeys key [key ...]时间复杂度:
L表示所有集合中元素的总数,N表示第一个集合的大小,K表示结果集合的大小。
返回值:目标集合中的元素个数。
这个命令需要6.2之后的版本,无法进行演示......
小结: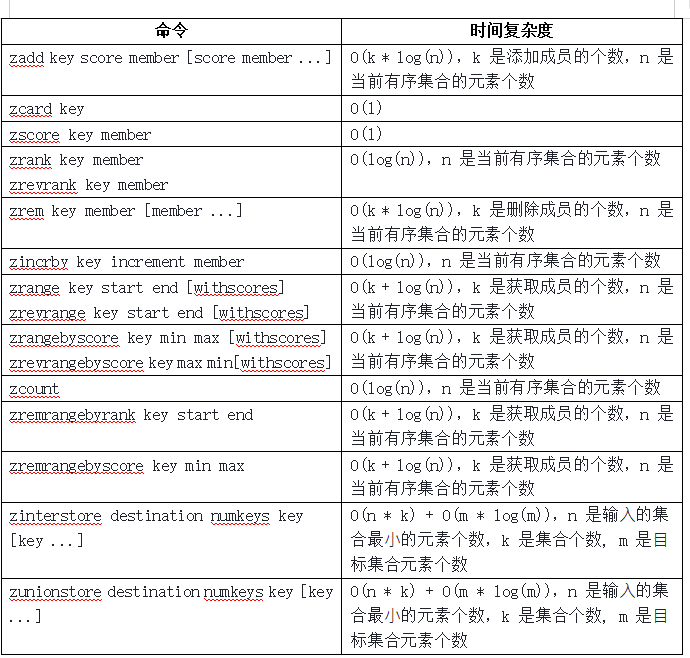
zset编码方式
如果有序集合中的元素个数较少,或者单个元素体积较小,使用ziplist来存储。=》压缩列表~~节省内存空间
如果当前元素个数较多,或者单个元素(member)体积较大,使用skiplist来存储了。
关于跳表
简单来说,跳表是一个"复杂链表"
查询时间复杂度:logN
相比于树形结构,更适合按照范围获取元素=》B+树
zset的应用场景
最关键的应用场景,排行榜系统。
排行榜场景又在很多地方有着用武之地:
1、微博热搜
2、游戏天梯排行
3、成绩排行
关键要点在于这里用来排行的"分数"是实时变化的,虽然这里是实时排行,但也需要高效地更新排行。
使用zset完成上述操作就非常简单~~比如游戏天梯排行,只需要把玩家信息和对应的分数放到有序集合中即可。自动就形成了一个排行榜,随时可以按照哦排行(下标),按照分数,进行范围查询~~
随着分数发生改变,也可以比较方便的,zincrby修改分数,排行顺序也能自动调整(logN)
那游戏玩家这么多,都用这个zset来存(内存),存得下吗?
就拿王者荣耀来举例吧,就按1亿玩家来算,就按userId 4 个字节,score 8个字节来存,表示一个玩家大概是12个字节。
12亿个字节 =》大概是1.2GB
啊?才1.2GB,那不是小case吗?
这里顺便教一下单位换算的技巧:
1000字节 = 1KB(千)
1000000字节 = 1MB(百万)
1000000000 = 1GB(十亿)
对于游戏排行榜,这里的前后顺序非常容易确定~~但是有的排行榜就要复杂些,比如:微博热度榜(需要综合浏览量、点赞量、转发量、评论量等维度),根据每个维度,计算得到综合得分才可以算出热度,此时就可以借助zinterstore/zunionstore按照加权方式处理了~~
此时就可以把上述每个维度的数值都放到一个有序集合中。member就是微博的id,score就是各自维度的数值~~
通过zinterstore或者zunionstore把上述有序集合按照约定好的权重,进行集合间运算即可~~得到的结果集合的分数就是热度。