【前后缀】Leetcode hot 100

文章目录

[LeetCode 238.除自身以外数组的乘积](#LeetCode 238.除自身以外数组的乘积)
[LeetCode 560.和为K的子数组](#LeetCode 560.和为K的子数组)
[LeetCode 121.买卖股票的最佳时机](#LeetCode 121.买卖股票的最佳时机)
[LeetCode 53.最大子数组和](#LeetCode 53.最大子数组和)

接雨水也算前后缀的题，只是在双指针那和盛水最多的容器写在了一起。

LeetCode 238.除自身以外数组的乘积

java 复制代码

class Solution {
    public int[] productExceptSelf(int[] nums) {
        int n = nums.length;
        int[] pre = new int[n];
        pre[0] = 1;
        for(int i = 1; i < n; i++){
            pre[i] = pre[i-1] * nums[i-1];
        }

        int[] suf = new int[n];
        suf[n-1] = 1;
        for(int i = n-2; i >= 0; i--){//注意这里是大于等于0，i--
            suf[i] = suf[i+1] * nums[i+1];
        }

        int[] ans = new int[n];
        for(int i = 0; i < n; i++){
            ans[i] = pre[i] * suf[i];
        }
        
        return ans;
    }
}

LeetCode 560.和为K的子数组

java 复制代码

class Solution {
    public int subarraySum(int[] nums, int k) {
        //sum(i,j)=k,也就是
        // s[j]-s[i-1] = k
        // s[i-1] = s[j]-k
        // 在 j 之前，有多少个 i-1 存在，使得 s[i-1] 的值恰好等于 s[j] - k。这里的s[j]包含nums[j]这个值！！和之前除自身以外数组的乘积那个题不一样！那个是左边所有元素的乘积
        int ans = 0;
        Map<Integer,Integer> prefixSumCounts = new HashMap<>();

        //注意这步
        prefixSumCounts.put(0, 1); //为了让s[i-1] = s[0-1] = s[-1]这种情况合法，因为要找0-j-1这些i里面符合s[j]-s[i-1] = k的数

        //用来维护s[j]的动态变化
        int currentPrefixSum = 0;

        for(int x:nums){
            //算s[j]
            currentPrefixSum += x;

            //算s[i-1]
            int targetPrefixSum = currentPrefixSum - k;
            //如果上面这个东西是0，同时x还是nums的第一个值，是存在那么1个的

            //找这个符合s[i-1]=s[j]-k(k=s[j]-s[i-1])的s[i-1]是否存在
            if(prefixSumCounts.containsKey(targetPrefixSum)){
                int count = prefixSumCounts.get(targetPrefixSum);
                ans+=count;
            }

            //存储s[j]
            // (1) 先获取 "currentPrefixSum" 之前出现过几次（默认为 0）
            int currentPrefixSumCnt = 0;
            if(prefixSumCounts.containsKey(currentPrefixSum)){
                currentPrefixSumCnt = prefixSumCounts.get(currentPrefixSum);
            }

            // (2) 在旧次数上 +1，然后存回哈希表
            prefixSumCounts.put(currentPrefixSum, currentPrefixSumCnt + 1);
        }
        return ans;
    }
}

思路总结：

其实这个没有维护一个前缀和数组，而是就是利用一个动态的值一次遍历计算前缀和，创造出了一个pre[nums[-1]]=0以便于求差计算（尤其是在子数组的情况下）！！因为会出现pre[n]-pre[0-1]也就是pre[n]-pre[-1]的情况

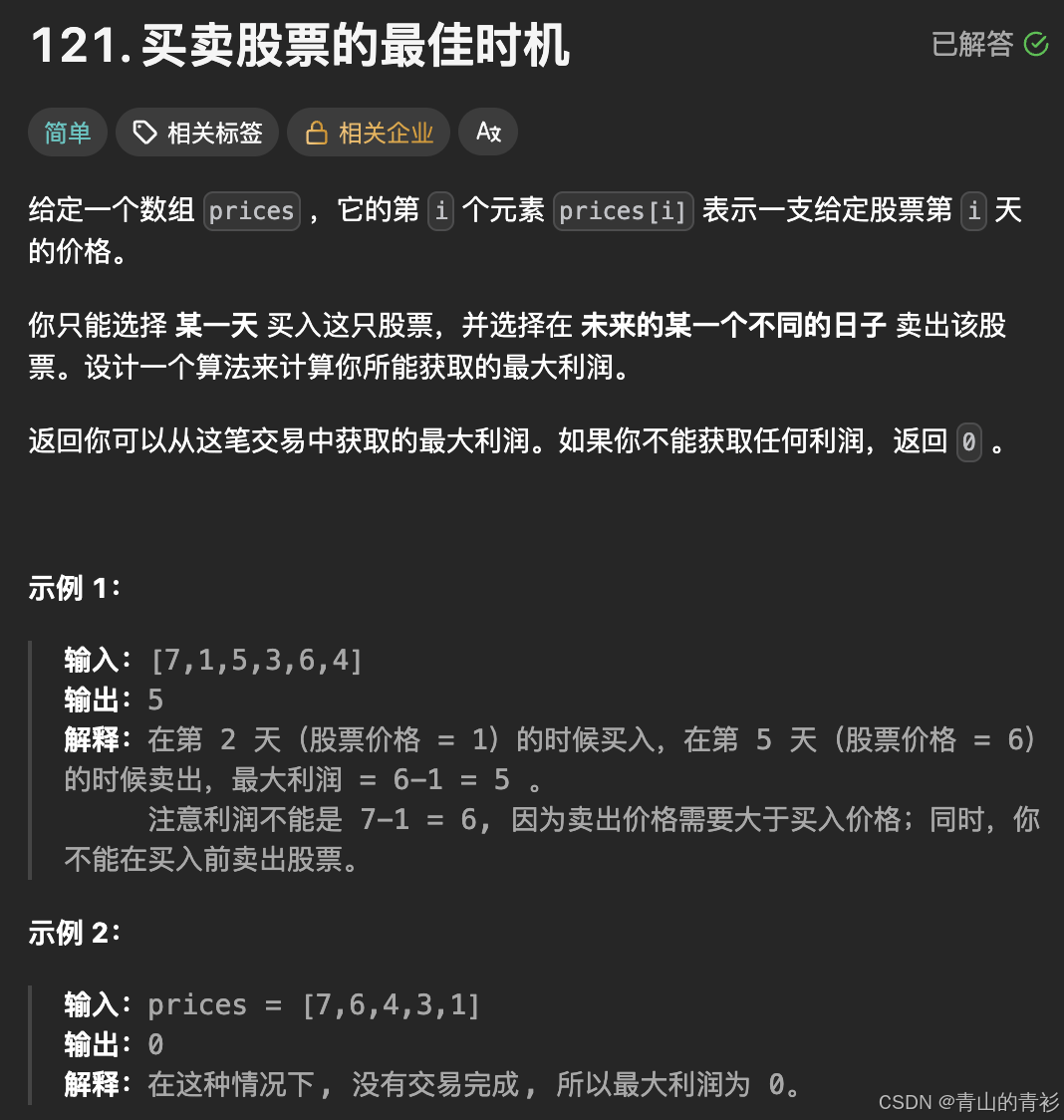
LeetCode 121.买卖股票的最佳时机

这题其实不算前缀和，算贪心，但是因为和53比较相似，也放进来了

java 复制代码

class Solution {
    public int maxProfit(int[] prices) {
        int ans = 0;
        int minPrice = prices[0];

        for(int p:prices){
            //注意先更新ans，后更新minPrice
            //先看如果今天卖能赚多少
            //再看要不要把今天当作新的最低价买点，使得后续能够用今天的价格计算
            //不然如果今天是历史最低点，这样算只考虑了今天买今天卖的情况，没有考虑之前买今天卖的情况
            ans = Math.max(ans, p-minPrice);
            minPrice = Math.min(minPrice,p);
        }
        return ans;
    }
}

思路总结：

主要就是注意先更新ans，后更新minPrice。

如果今天是历史最低点，先更新minPrice的话，只考虑了今天买今天卖的情况，没有考虑之前买今天卖的情况。不过题目也有要求，"你只能选择某一天买入这只股票，并选择在未来的某一个不同的日子卖出该股票。"

LeetCode 53.最大子数组和

java 复制代码

class Solution {
    public int maxSubArray(int[] nums) {
        int ans = Integer.MIN_VALUE;
        int minPreSum = 0;
        int preSum = 0;

        for(int x : nums){
            preSum += x;
            //先更新ans，后更新minPreSum
            //不然类比股票，只考虑了今天买今天卖的情况，没有考虑之前买今天卖的情况
            //而且这样会把当前前缀和误当成最小前缀和，导致计算出非法的空子数组，因为题目约束子数组最小为1
            ans = Math.max(ans, preSum-minPreSum); // 减去前缀和的最小值
            minPreSum = Math.min(minPreSum,preSum);// 维护前缀和的最小值
        }

        return ans;
    }
}

思路总结：

一边遍历数组计算前缀和，一边维护前缀和的最小值，用当前的前缀和减去前缀和的最小值，就得到了以当前元素结尾的子数组和的最大值，用它来更新答案的最大值。

由于题目要求子数组不能为空，应当先计算前缀和-最小前缀和，再更新最小前缀和。相当于不能在同一天买入股票又卖出股票。