leetcode 2536 - 技术栈

2536: 子矩阵元素加1

思路1：暴力解

复制代码

class Solution {
public:
    vector<vector<int>> rangeAddQueries(int n, vector<vector<int>>& queries) {
        vector<vector<int>> ans(n,vector<int>(n,0));
        for(auto& qur :queries){
            for(int i=qur[0];i<=qur[2];i++){
                for(int j=qur[1];j<=qur[3];j++){
                    ans[i][j]++;
                }
            }
        }

        return ans;
    }
};

思路2：二维差分+二维前缀和

一维差分，见 leetcode 2528

使用二维差分数组diff，其中diff[i][j]表示原数组mat[i][j]到mat[n-1][n-1]每个元素++变化值。++

例如将mat[x1][y1]到mat[x2][y2]每个元素值加一，反映到差分数组上就表现为：

diff[x1][y1]+=1，先从mat[x1][y1]到mat[n-1][n-1]每个元素都加一

diff[x2+1][y1]−=1，由于从mat[x2+1][y1]到mat[n-1][n-1]每个元素无需改变，第一步加的范围太大了，不该变的撤销变化

diff[x1][y2+1]−=1，与2同理，由于从mat[x1][y2+1]到mat[n-1][n-1]每个元素无需改变，第一步加的范围太大了，不该变的撤销变化

diff[x2+1][y2+1]+=1，由于第二步和第三步都包含范围mat[x2+1][y2+1]，所以这块"重复撤销"了，再加回来

对于每个query，以O(1)的时间复杂度可以计算出diff数组的变化。最终处理完所有query，再由diff差分数组反推出原数组mat就好了。

代码实现时，为方便计算二维前缀和，可以在二维差分矩阵最上面添加一行 0，最左边添加一列 0，这样计算二维前缀和无需考虑下标越界。

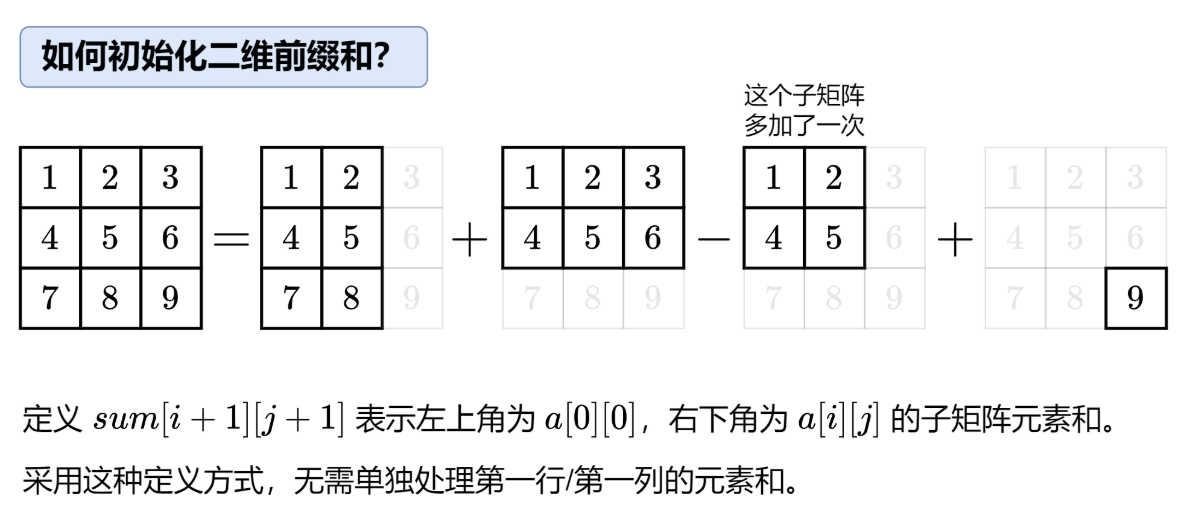
公式
diff[i][j] = diff[i][j] + diff[i-1][j] + diff[i][j-1] - diff[i-1][j-1]

正是二维前缀和递推式。

class Solution {
public:
vector<vector<int>> rangeAddQueries(int n, vector<vector<int>>& queries) {
/*二维差分，记录差分数组的变化
二维矩阵a的区域+1操作，等价于更新差分矩阵d中4个位置的差分值。
为方便计算二维前缀和，在二维差分矩阵上下左右各添加一行0 */
vector<vector<int>> diff(n+2,vector<int>(n+2)); //防止越界
for(auto& q :queries){
int r1=q[0],c1=q[1],r2=q[2],c2=q[3];
diff[r1+1][c1+1]++;
diff[r1+1][c2+2]--;
diff[r2+2][c1+1]--;
diff[r2+2][c2+2]++;
}
复制代码
```
      // 原地计算 diff 的二维前缀和，然后填入答案
      vector<vector<int>> ans(n,vector<int>(n));
      for(int i=0;i<n;i++){
          for(int j=0;j<n;j++){  
              diff[i+1][j+1]+=diff[i][j+1]+diff[i+1][j]-diff[i][j];
              ans[i][j]=diff[i+1][j+1];
          }
      }

      return ans;
  }
```
};