树与图的深度优先遍历
树是特殊的无环连通图
图分成有向图和无向图(a-b 建a->b和b->a)
有向图可以用邻接矩阵(g[a][b] == a->b)和邻接表(存储每个点直接到达的所有点,h[N]存储每个位置头结点,每次加入边都在头结点加入)两种表达方式。
txt
假设要构建一个无向图,包含边 1-2、1-3、2-4,执行过程如下:
初始状态:h[1]=-1、h[2]=-1、h[3]=-1、h[4]=-1,idx=0;
执行 add(1,2):
e[0]=2、ne[0]=-1(新节点指向空)、h[1]=0、idx=1;
此时 1 的邻接链表:1 -> 2;
执行 add(1,3):
e[1]=3、ne[1]=0(新节点指向原来的表头 0)、h[1]=1、idx=2;
此时 1 的邻接链表:1 -> 3 -> 2(头插法,新节点插在最前面);
执行 add(2,4):
e[2]=4、ne[2]=-1、h[2]=2、idx=3;
此时 2 的邻接链表:2 -> 4对于邻接表
java
M=N*2
int h[N],e[M], ne[M], idx;
boolean st[N];//表示点是否被走过
void add(int a, int b){//给节点 a 新增一个邻接节点 b
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
// 需要标记数组st[N], 遍历节点的每个相邻的便
void dfs(int u) {
st[u] = true; // 标记一下,记录为已经被搜索过了,下面进行搜索过程
for (int i = h[u]; i != -1; i = ne[i]) {
int j = e[i];
if (!st[j]) {
dfs(j);
}
}
}树的重心
思路:
找出每个点去掉后,它的剩余联通块的点数的最大值,然后遍历得到其中最大值的最小值是多少
每次当前节点保存该节点的子树的点的数量,对于每个节点,父节点那一坨 = n − s i z e n =n-size_n =n−sizen
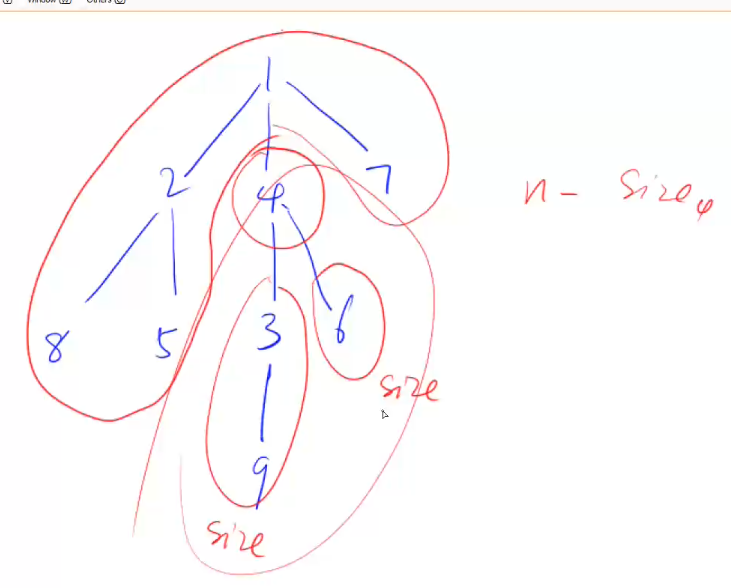
代码
java
import java.util.*;
public class Main{
static int N = 100010,M = N * 2,idx,n;
static int[] h = new int[N];
static int[] e = new int[M];//存的是双倍,所以是M
static int[] ne = new int[M];//存的是双倍,所以是M
static boolean[] st = new boolean[N];
static int ans = N; //一开始将最大值赋值成N,最大了
/***
* 邻接表,存储方法
* 邻接表不用管执行顺序,只需要知道每个节点能够执行到每个多少个节点就行
* 比如案例中4 3 , 4 6 ,头结点4插入两个节点3和6,所以执行到4就能够执行3和6,
* 固定的,邻接表就是这样子的
***/
public static void add(int a,int b){
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
//返回的是当前子树的数量,比如1下面的所有数量包括自己就是9
public static int dfs(int u){
int res = 0;//连通块中的最大值这个其实就是ans,到时候跟ans比较大小,小的话就赋值给ans的
st[u] = true;//将这个删除的点标记,下次不在遍历
int sum = 1;//将删除的点也算上是初始值就是1;到时候有利于求n-sum;
//单链表遍历
for(int i = h[u];i != -1 ; i = ne[i]){
int j = e[i];//然后将每一个的指向的点用变量表示出来
if(!st[j]){ //然后如果是没用过,没被标记过的,就可以执行
int s = dfs(j);//然后递归他的邻接表上面所有能够抵达的点
//然后返回的数量是他所删除的点下面的连通块的大小
res = Math.max(res,s); //然后和res比较一下大小,谁大谁就是最大连通块
sum += s; //这里是将每递归一个点,就增加一个返回的s,就可以将这个值作为返回值成为最大连通块
}
}
/***
* 因为邻接表表中只是往下面执行,删除的点的上面的连通块可能是最大的连通块,
* 所以需要用总数减去我们下面所统计出来的最大的连通块
* 然后将最大的连通块的值赋值给res
* **/
res = Math.max(res,n-sum);
//然后将每个次的最大值进行比较,留下最小的最大值
ans = Math.min(res,ans);
return sum;
}
public static void main(String[] ags){
Scanner scan = new Scanner(System.in);
n = scan.nextInt();
//这里是将每一个头节点都赋值成-1
for(int i = 1 ; i < N ; i++ ){
h[i] = -1;
}
//案例输入输出
for(int i = 0 ; i < n - 1 ; i ++){
int a = scan.nextInt();
int b = scan.nextInt();
//因为是无向边,所以就两个数同时指向对方
add(a,b);
add(b,a);
}
dfs(1);//从1开始
//最后输出的是最小的最大值
System.out.println(ans);
}
}树与图的广度优先遍历
图中点的层次
思路
最短路径都参考bfs写法,队列引入更新距离矩阵d
代码
java
import java.util.*;
public class Main{
static int N = 100010,M = N * 2,idx,hh,tt,n,m;
static int[] h = new int[N];
static int[] e = new int[M];//存的是双倍,所以是M
static int[] ne = new int[M];//存的是双倍,所以是M
static int[] d = new int[M];//1->n的距离
//初始化队列
static int[] q = new int[N];
public static void add(int a,int b){
e[idx]=b;ne[idx]=h[a];h[a]=idx++;
}
public static int bfs(){
hh=0;tt=-1;//初始化 放入1号点
q[++tt]=1;
d[1]=0;
while(hh<=tt){
int t = q[hh++];
for(int i=h[t];i!=-1;i=ne[i]){
int j = e[i];
if(d[j]==-1){
d[j]=d[t]+1;
q[++tt]=j;
}
}
}
return d[n];
}
public static void main(String[] ags){
Scanner scan = new Scanner(System.in);
n = scan.nextInt();
m = scan.nextInt();
for(int i = 1;i<N;i++){
h[i]=-1;
d[i]=-1;
}
while(m-->0){
int a = scan.nextInt();
int b = scan.nextInt();
add(a,b);
}
System.out.println(bfs());
}
}