在计算机视觉领域,单个像素常常会成为我们测量能力的极限------但这并非无法突破。在计量学和精密机器人等领域,哪怕仅仅一个像素的误差,都可能转化为微米级的实际偏差。为了突破传感器物理极限,工程师们采用了一种强大的技术:亚像素边缘检测。
亚像素边缘检测并非要换用更好的相机,而是要从相同的像素中提取更多信息。通过建模相邻像素间的灰度变化规律,我们可以用数学方法估算出边缘的精确位置,实现亚像素级精度。本文将深入解析亚像素边缘检测的原理、背后的数学基础,以及它为何能成为高精度视觉系统的核心技术。
"亚像素"到底是什么?
每张数字图像都由离散的像素点组成,这些微小方格记录了亮度或颜色信息。传统的边缘检测算法(如Sobel、Prewitt或Canny)通过识别像素值的剧烈变化来定位边缘,最终得到的是像素级的二值边缘图:边缘要么穿过某个像素,要么不穿过。来看下面这张圆形和矩形的示例图:

以下是像素级和亚像素级边缘检测效果的对比:


可以看出,亚像素操作能让我们将边缘定位到其真实的几何位置,而不再受限于离散的像素网格。
结果是,我们得到了更平滑、更连续的轮廓线,能更好地还原场景中的真实形状。圆形变得更圆润,直线更笔直,角落位置也精准无误。
在深入探讨亚像素世界之前,我们得先理解边缘的定义以及如何进行初步的边缘检测。
理解边缘与梯度
我们从一个简单的例子开始:想象一张半黑半白的图片,中间有一条清晰锐利的分界线------这就是我们所说的边缘。

这条分界线就是图像中灰度值发生突变的地方,从暗到亮,或从亮到暗。如果你沿着一条水平线绘制穿过这条边界的亮度值,你会看到一个突然的跳跃:一段平坦的黑像素区域,一个急剧上升的过渡区,然后又是一段平坦的白像素区域。
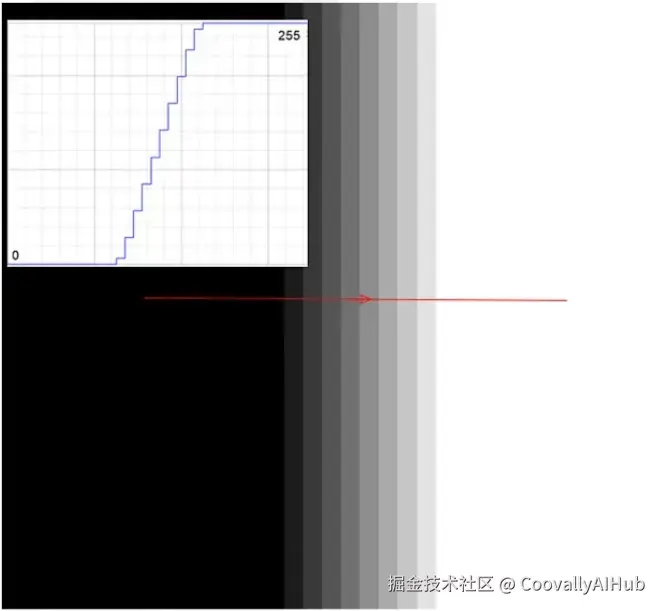
本质上,边缘就是灰度值发生急剧变化的位置。它们是图像在告诉我们"这里有变化"。无论是物体的轮廓、阴影边界还是纹理变化,所有这些都通过灰度的变化来定义。
那么,如何量化像素间的这种突变呢?
一个简单的思路是查看每个像素与其相邻像素的差异。
如果我们用一个像素的灰度值减去它前一个像素的值,就能得到一个反映该点亮度变化程度的数值。
换句话说,我们计算的是相邻像素之间的差值------这本质上就是导数的概念。正如微积分中导数衡量函数变化快慢一样,在图像中,它衡量的是灰度在空间上的变化速度。
当这个差值(或导数)很大时,我们就知道找到了一个边缘。平坦区域的变化很小或为零;而边缘处则存在强烈的突变。
这正是梯度概念的用武之地。我们刚才计算的差值只反映了一个方向上的变化,但图像可能在多个方向上同时发生变化。梯度将导数的概念扩展到了二维空间------它是一个向量,同时捕捉了变化的大小和方向。
用数学术语来说,图像 I(x, y) 的梯度表示为:

其中:
- ∂I/∂x 衡量的是水平方向上的亮度变化(x方向梯度),
- ∂I/∂y 衡量的是垂直方向上的亮度变化(y方向梯度)。
为了估算这些偏导数,我们可以使用小的卷积核(滤波器),例如:

如果你不熟悉图像处理,卷积操作 听起来可能有点复杂,但其实很简单。可以把它想象成一个小的"窗口"或滤波器,在图像上滑动,通过结合邻域像素的值来计算中心像素的新值。
当我们把上述的 Gx 滤波器应用到我们的黑白图像时,可以观察到:
- 平坦区域(亮度均匀)产生零或极低的值,因为相邻像素间几乎没有变化。
- 过渡区域(亮度急剧跳跃)产生高值,表明像素强度发生了强烈变化。

根据这些水平和垂直方向的变化,我们可以计算出两个基本量:梯度幅值 和 梯度方向,定义如下:

幅值告诉我们变化的强度(边缘的明显程度),而方向则指向边缘的朝向。之后,我们可以对梯度幅值图像设定一个阈值来判定每个像素是否为边缘点,或者像Canny边缘检测那样使用双阈值滞后法来进行判断。
至此,我们大致了解了梯度如何揭示图像发生变化的位置和锐利程度,以及这些变化如何定义边缘。现在,我们可以深入探讨由Von Gioi和Randall改进的Devernay方法 [1],进入亚像素的世界。
Devernay亚像素边缘检测方法
我们可以将Devernay方法视为Canny算法的改进版。因为Devernay方法遵循了相似的哲学,但更进一步。因此,算法步骤看起来很相似,但包含了一些不同的操作。
- 算法步骤:
- 高斯模糊:首先应用高斯模糊来抑制噪声、平滑灰度变化,使梯度计算更稳定。
- 计算X和Y方向梯度及幅值:这就是我在"理解边缘与梯度"部分解释的内容。
- 计算边缘点:这是Devernay方法的核心,执行亚像素校正。因此我将进行详细解释。
- 连接边缘点:将属于同一边缘的点连接成链。
- 滞后阈值处理:滤除噪声产生的虚假边缘,保留真实的边缘链。
第三步(计算边缘点)的算法工作原理如下:
对于每个像素点:
获取当前像素的上、下、左、右四个邻域像素值。
如果当前像素值大于其左 和 右邻域像素值:
这意味着在当前像素的水平3像素邻域内,它是峰值。
如果当前像素值大于其上 和 下邻域像素值:
这意味着在当前像素的垂直3像素邻域内,它是峰值。
如果该像素在水平或垂直方向上是峰值:
则进行二次插值计算,以精确定位边缘。
为了详细说明,我们使用之前的黑白图像。当你在完成前两步后对图像进行放大观察,你会看到类似下面的输出:

假设算法当前正在处理图像中心的像素。我们会看到下图所示的值。可以想象,当前像素值大于其左边和右边的像素值。在这种情况下,它将进入"计算二次插值"的步骤。

这对应于沿着梯度方向(假设是水平方向)的三个像素点。然后,我们通过这三个样本点拟合一条抛物线,并找到其顶点(即最大值),这个顶点就是像素之间的真实边缘位置。
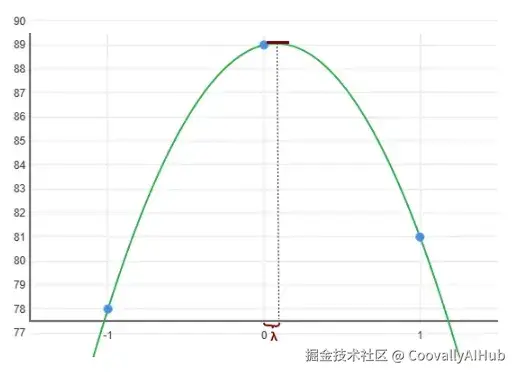
这些点代表了梯度强度在相邻像素间的变化情况:中心点 (x = 0) 对应当前像素,-1 和 +1 位置对应其邻居。
平滑的绿色曲线是通过这三个样本点拟合出的抛物线。这条曲线的真实最大值(用小红线标记)对应抛物线的顶点,它指示了边缘的实际位置。因为梯度最大值所在的位置就是变化最剧烈的地方。
顶点的x坐标值也意味着相对于中心像素的偏移量 (λ),因为中心像素被定位在 x = 0。在这个例子中,顶点正好在中心像素上方,所以偏移量 (λ) 接近于零。你可以在下图中看到输出点的位置。

如果曲线的峰值略微偏左或偏右,λ就会是一个小的负值或正值,意味着实际的边缘位于像素之间。
- 如果 λ = 0 → 最大值正好在像素中心。
- 如果 λ > 0 → 边缘略微朝向 +1 方向的像素。
- 如果 λ < 0 → 边缘更靠近 -1 方向的像素。
根据Devernay [2]的说法,λ可以通过以下公式计算:
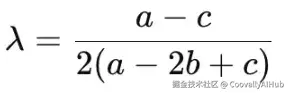
我们知道 f(−1) = a, f(0) = b, f(1) = c。对于我们这个例子,a = 78, b = 89, c = 81。因此可以算出 λ ≈ 0.078。正如我所说,它接近零。但在精确的圆形边缘过渡处,你可能会看到其他情况(峰值不在像素正中心),如下图所示。
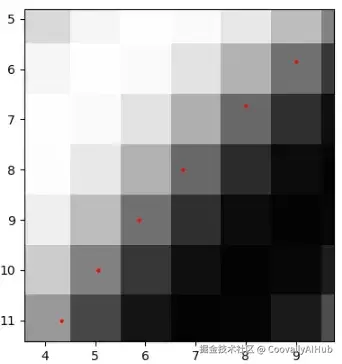
因此,对于每个进入if条件的像素,都会计算这个偏移值,然后通过将偏移值加到该像素的x或y坐标上,来定义新的亚像素边缘位置。这就是第三步的工作原理,正如你所想象的,这是亚像素校正的关键部分。
第四步是连接过程,也称为"链边缘点"。每个边缘点(来自第三步)都是独立计算出来的,属于同一条边缘的点需要被连接起来,形成对应于图像轮廓的曲线。因此,算法会将一个边缘点连接到距离最近的其他边缘点(距离不超过某个容差范围内)。
它检查当前边缘点周围5x5邻域内的其他边缘点,并找到那些与当前点梯度方向相似的点。当你把这些点收集到一个集合中,并找到与当前点距离最小的那个点时,你就可以像下面这样将这些点连接起来:

这样就确保了只有属于同一物理轮廓的点才会被连接起来,从而产生平滑、连贯的边缘曲线。
第五步,滞后阈值处理:在检测并连接完所有亚像素边缘点之后,接下来的挑战是判断哪些边缘是可靠的,哪些只是噪声。这最后一步应用了一个称为滞后阈值法的过程,类似于Canny边缘检测器中使用的方法。
对于每个边缘点 e,如果其梯度幅值 |g(e)| 大于或等于高阈值 (H),则将其标记为有效。这个点被视为"强边缘"。
从每个强边缘点出发,算法沿着已连接的边缘链移动:
如果下一个连接点的梯度幅值仍然高于低阈值 (L),那么它也被标记为有效。
这个过程持续进行,直到链上的点其梯度幅值低于 L 为止。
因此,与强边缘相连的弱边缘得以保留,而孤立的弱响应则被忽略。
最后,在此过程之后仍然未被标记为有效的任何边缘点,将从边缘点列表中解除链接并彻底移除。
这就是改进版Devernay算法的大致工作方式!算法的输出效果可以在下面的示例图中看到:

通过结合梯度分析、边缘链接和滞后阈值处理,这种方法将原始的图像梯度转化为了精确、连续的边缘轮廓,可直接用于任何高精度的计算机视觉应用中。