实现链式结构二叉树--递归中的暴力美学（第13讲）

一.堆的应用

1.1 堆排序（上一篇文章已经讲过啦~）

1.2 TOP-K问题

TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。比如：专业前10名，世界500强，富豪榜，游戏中前100的活跃玩家等等。

对于TOP-K问题，能想到的最简单直接的方式就是排序，但是，如果数据量非常大，排序就不太可取了（可能数据都不能一下子全部加载到内存中）。最佳的方式就是用堆来解决。

灵魂拷问：假设现在有10亿个整数，求前K个最大的数，需要申请多大内存？

答：我们知道，1G=1024KB=1024*1024KB=1024*1024*1024byte≈10亿，一个整数四个字节，所以十亿个整数要消耗10亿*4=4G的空间。

假设现在只有1G内存，咋办？

思路：可以先把10亿个数据平均分成四等分，第一份先拿来建堆（消耗1G的空间），取最大的前几个数据，然后第二份数据再拿来建堆，再取最大的前几个数据，依此类推...

假设现在只有1KB内存咋办？

思路：找最大的前K个数据，取这些数据的前K个数（注：无顺序排列）建小堆，遍历剩下的数据和堆顶比，如果比堆顶小，继续往后遍历，如果比堆顶大，就和堆顶交换，继续遍历，最后堆中的K个元素就是十亿个数据中前K个最大的数。

如果要找最小的前K个数据，建大堆，遍历剩下的数据和堆顶比，比堆顶小就和堆顶交换。

//找最大的前K个数
void TopK()
{
	int k = 0;
	printf("请输入K：\n");
	scanf("%d", &k);
	const char* file = "data.txt";
	FILE*fout=fopen(file, 'r');//打开文件，为只读模式;fout接收返回值
	//如果文件打开失败
	if (fout == NULL)
	{
		perror("fopen fail");
		exit(1);
	}
	//申请空间大小为K的整型数组--建小堆
	int* minHeap = (int*)malloc(sizeof(int)*k);
	if (minHeap == NULL)
	{
		perror("malloc fail");
		exit(2);
	}
	//读取文件K个数据放到数组中
	for (int i = 0; i < k; i++)
	{
		fscanf(fout, "%d", &minHeap[i]);
	}
	//数组调整建堆-向下调整算法
	//找最大的前k个数，建小堆
	for (int i = (k - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(minHeap, i, k);

	}
	//遍历剩下的n-k个数，跟堆顶比较，谁大谁入堆
	int data = 0;//将剩下数据保存到data中
	while (fscanf(fout, "%d", &data) != EOF)
	{
		if (data > minHeap[0])
		{
			minHeap[0] = data;
			AdjustDown(minHeap, 0, k);
		}
	}
	//打印堆里的值
	for (int i = 0; i < k; i++)
	{
		printf("%d", minHeap[i]);
	}
	printf("\n");
	fclose(fout);//打开文件一定要记得最后关闭
}

---

二. 实现链式结构二叉树

用链表来表示一棵二叉树，即用链来指示元素的逻辑关系。通常的方法是链表中的每个节点由三个域组成，数据域和左右指针域，左右指针分别用来给出该节点左孩子和右孩子所在的链结点的存储地址。

#pragma once
#include <stdio.h>
#include <stdlib.h>
typedef int BTDataType;
//定义二叉树节点结构
typedef struct BinaryTreeNode {
	int data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode; 

回顾二叉树的概念，二叉树分为空树和非空二叉树，非空二叉树由根节点，根节点的左子树，根节点的右子树组成。根节点的左子树和右子树分别是由子树节点，子树节点的左子树 ，子树节点的右子树组成的，因此二叉树定义是递归式的。

（一）前中后序遍历

二叉树的操作离不开树的遍历，我们先看看二叉树的遍历有哪些方式。

2.1.1遍历规则

①前序遍历 ：先遍历根节点，再遍历左子树，最后遍历右子树----根左右（先根遍历）

②中序遍历：先遍历左子树，再遍历根节点，最后遍历右子树----左根右

③后序遍历：先遍历左子树，再遍历右子树，最后遍历根节点----左右根

④层序遍历：按照层次依次遍历----从上到下，从左到右

注：前/中/后序遍历都属于深度优先遍历，层序遍历属于广度优先遍历。

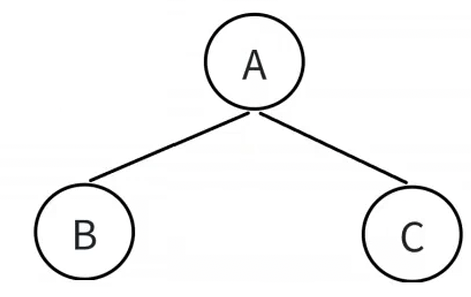
前序遍历：A->B->C 中序遍历：B->A->C

后序遍历：B->C->A 层序遍历：A->B->C

小试牛刀：

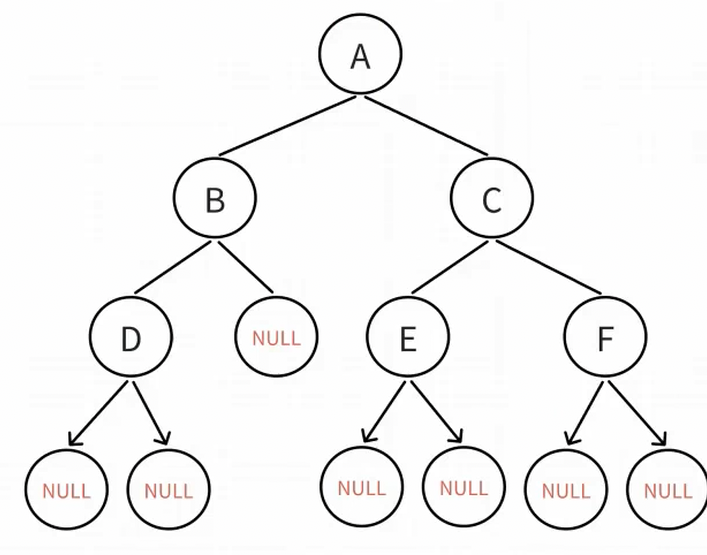
前序遍历：A->B-> D-> NULL-> NULL ->NULL-> C-> E ->NULL ->NULL ->F ->NULL-> NULL

中序遍历：NULL->D->NULL->B->NULLA->NULL->E->NULL->C->NULL->F->NULL

后序遍历：NULL->NULL->D->NULL->B->NULL->NULL->E->NULL->NULL->F->C->A

2.1.2 代码实现

(1) 前/中/后序遍历

//1.前序遍历
void PreOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%c ", root->data);
	PreOrder(root->left);
	PreOrder(root->right);
}
//2.中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	PreOrder(root->left);
	printf("%c ", root->data);
	PreOrder(root->right);
}
//3.后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	PreOrder(root->left);
	PreOrder(root->right);
	printf("%c ", root->data);
}

（2）求二叉树有效节点个数（三种写法）

//4.求二叉树有效节点个数
int size = 0;
int BinaryTreeSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	size++;
	BinaryTreeSize(root->left);
	BinaryTreeSize(root->right);
	return size;
}
//5.二叉树节点个数
int Binarytreesize(BTNode* root,int* psize)
{
	if (root == NULL)
	{
		return 0;
	}
	(*psize)++;
	Binarytreesize(root->left,psize);
	Binarytreesize(root->right,psize);
}
//6.二叉树节点总数
int BinaryTreeDeepth(BTNode* root)
{
	return 1 + BinaryTreeDeepth(root->left) + BinaryTreeDeepth(root->right);
}

（3）二叉树叶子结点个数

/7.二叉树叶子结点个数
int BinaryTreeLeafsize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	return BinaryTreeLeafsize(root->left) + BinaryTreeLeafsize(root->right);
}

（4）二叉树第k层节点个数

//8.二叉树第K层节点个数
int BinaryTreeKsizenode(BTNode* root,int k)
{
	if (root == NULL)
	{
		return 0;
	}
	//判断是否为第k层
	if (k == 1)
	{
		return 1;
	}
	return BinaryTreeKsizenode(root->left, k - 1) + BinaryTreeKsizenode(root->right, k - 1);
}

（5）二叉树高度/深度

//9.二叉树的高度/深度
int BinaryTreedepth(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	int leftdep = BinaryTreedepth(root->left);
	int rightdep = BinaryTreedepth(root->right);
	return (leftdep > rightdep ? leftdep : rightdep) + 1;
}

（6）二叉树的销毁

//11.二叉树销毁(后序遍历)
void BInaryTreeDestory(BTNode** root)
{
	if (*root == NULL)
	{
		return;
	}
	BInaryTreeDestory(&((*root)->left));
	BInaryTreeDestory(&((*root)->right));
	free(*root);
	*root = NULL;
}

2.1.3 层序遍历

思路：借助数据结构--队列。将根节点保存在队列中，使队列不为空，循环判断队列是否为空，不为空取队头，将队头节点不为空的孩子结点入队列。

//12.层序遍历--借助队列结构
void LevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		//取队头，打印队头,出队头
		BTNode* top = QueueFront(&q);
		printf("%c ", top->data);
		QueuePop(&q);
		//再将队头节点不为空的孩子结点入队列
		if (top->left != NULL)
			QueuePush(&q, top->left);
		if (top->right != NULL)
			QueuePush(&q, top->right);
	}

	QueueDestory(&q);
}

2.1.4 判断二叉树是否为完全二叉树

思路：借助数据结构--队列。根节点先入队列，保证队列不为空，循环判断队列是否为空，不为空取队头，出队头，将队头节点的左右孩子都入队列。若最后队列中既有非空节点，又有空节点，则为非完全二叉树；若队列中最后只有非空节点，则为完全二叉树。

//13.判断是否为完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		//取队头，出队头
		BTNode* top = QueueFront(&q);
		QueuePop(&q);
		if (top == NULL)
		{
			//top取到空就直接出队列
			break;
		}
		//将队头节点的左右孩子入队列
		QueuePush(&q, top->left);
		QueuePush(&q, top->right);
	}
	//队列不为空，继续取队列中的队头
	while (!QueueEmpty(&q))
	{
		BTNode* top = QueueFront(&q);
		QueuePop(&q);
		if (top != NULL)
		{
			//不是完全二叉树
			return false;
		}
	}
	QueueDestory(&q);
	return true;
}