一、树的存储结构
1.1 树的逻辑结构回顾
- 树的逻辑结构
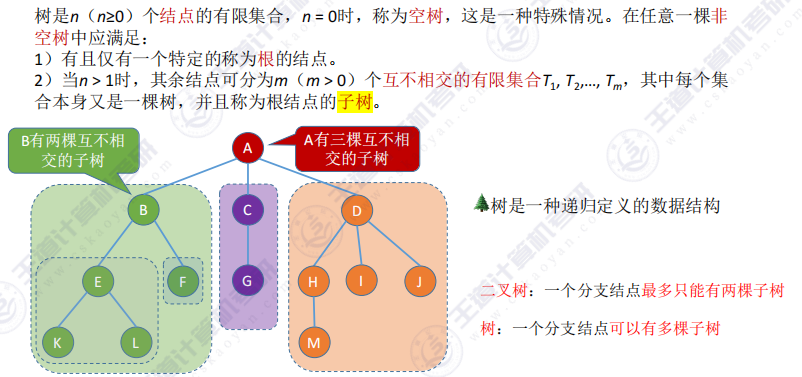
- 二叉树的存储结构
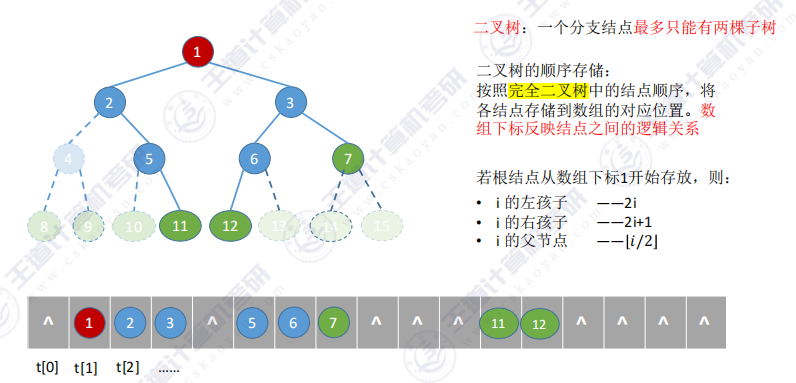
- 使用二叉树的顺序存储法,无法反映树的逻辑关系
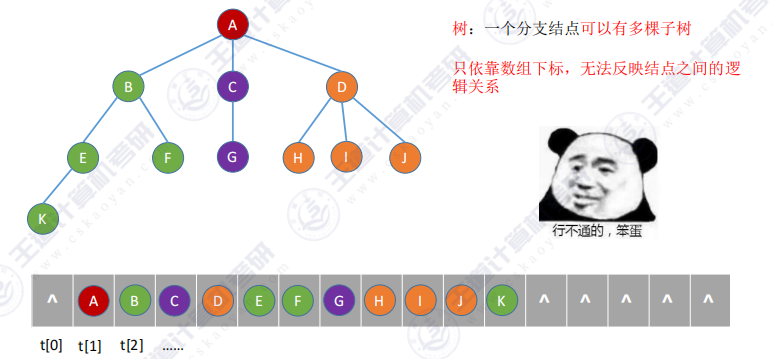
1.2 双亲表示法(顺序存储)
-
思路:用数组顺序存储各个结点,每个结点中保存数据元素、指向双亲结点(父节点)的"指针"
-
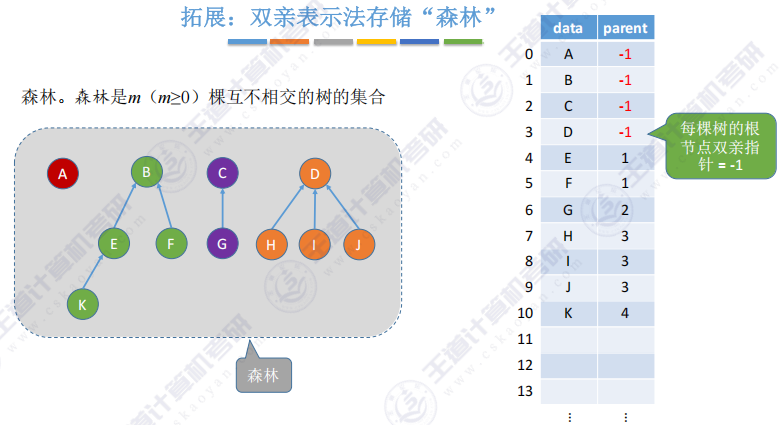
根节点的双亲指针 = -1(如下图"parent"的-1,表示A为根节点)
-
非根节点的双亲指针 = 父节点在数组中的下标 (如下图的"parent"的1,表示E的父节点是B,B的数组下标为1)

-
双亲表示法存储森林
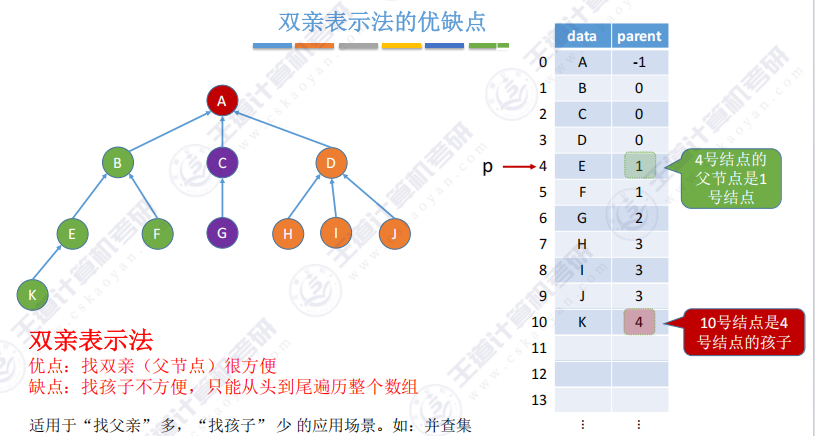
- 双亲表示法的优缺点
优点 :找双亲(父节点)很方便
缺点:找孩子不方便,只能从头到尾遍历整个数组
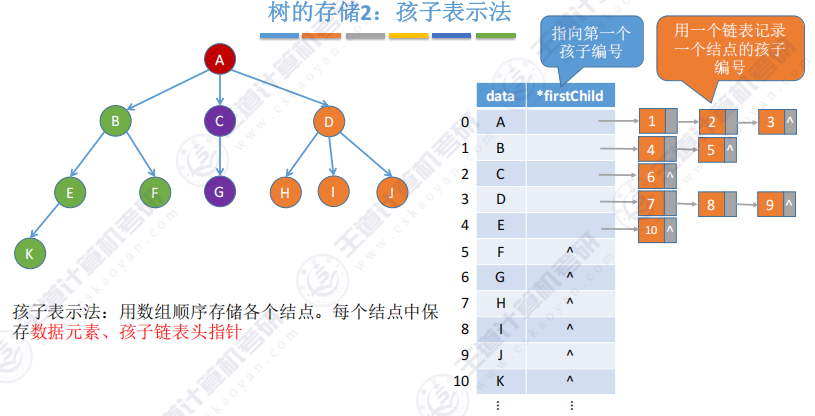
1.3 孩子表示法(顺序+链式存储)
- 孩子表示法:用数组顺序存储各个结点。每个结点中保存数据元素、孩子链表头指针
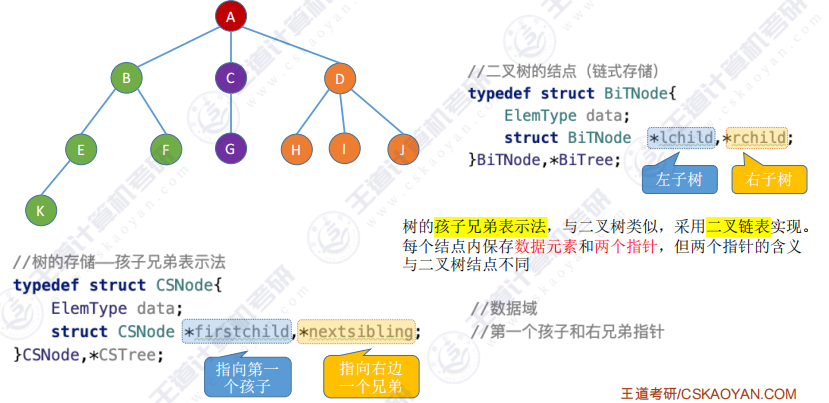
1.4 孩子兄弟表示法(链式存储)
- 孩子兄弟表示法 :与二叉树类似,采用二叉链表实现。每个结点内保存数据元素 和两个指针 ,但两个指针的含义与二叉树结点不同
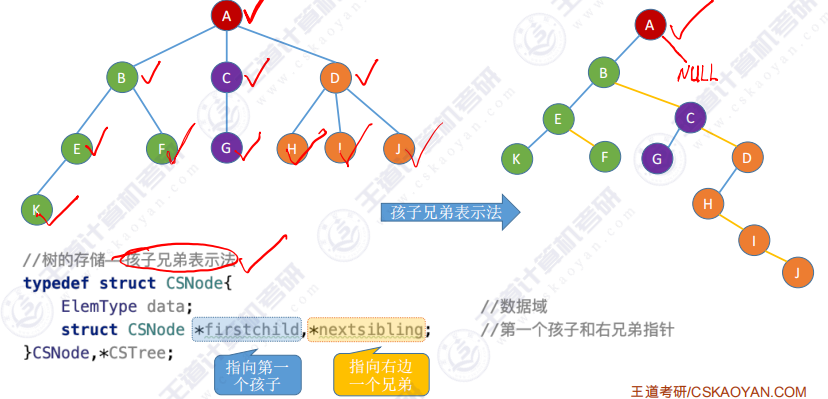
- 树的孩子兄弟表示法存储
- 森林的孩子兄弟表示法存储
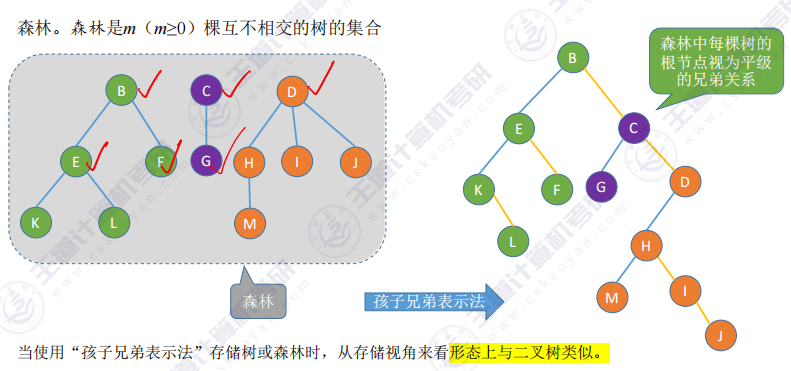
1.5 总结
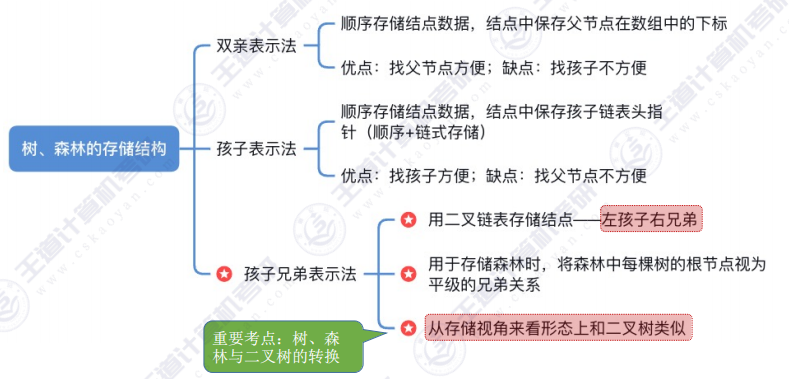
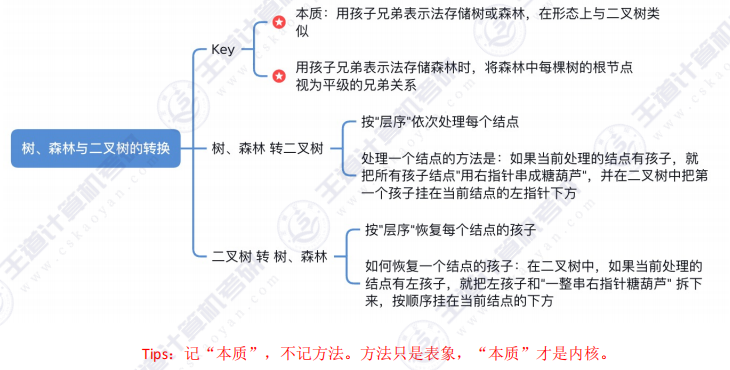
二、树、森林和二叉树的转换
2.1 树转二叉树
- 转换规则 :"左孩子,右兄弟"。先在二叉树中,画一个根节点,再按"树的层序"依次处理每个结点。
- 处理一个结点的方法:如果当前处理的结点在树中有孩子,就把所有孩子结点"用右指针串成糖葫芦",并在二叉树中把第一个孩子挂在当前结点的左指针下方
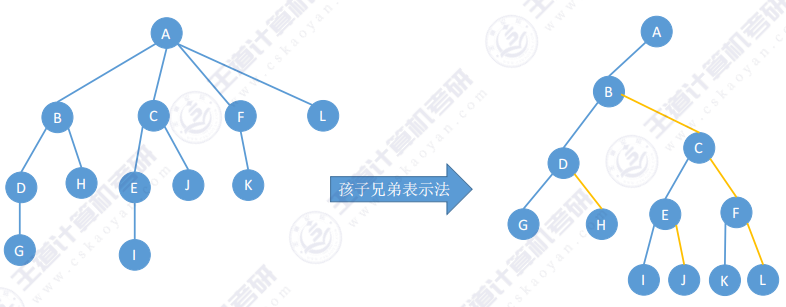
2.2 森林转二叉树
- 转换规则 :"左孩子,右兄弟"。先把所有树的根结点画出来,在二叉树中用右指针串成糖葫芦 ,再按"森林的层序"依次处理每个结点。
- 处理一个结点的方法:如果当前处理的结点在树中有孩子,就把所有孩子结点"用右指针串成糖葫芦",并在二叉树中把第一个孩子挂在当前结点的左指针下方
- 注意 :森林中各棵树的根节点视为平级的兄弟关系
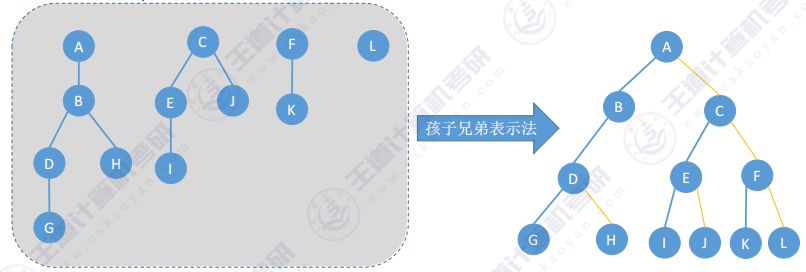
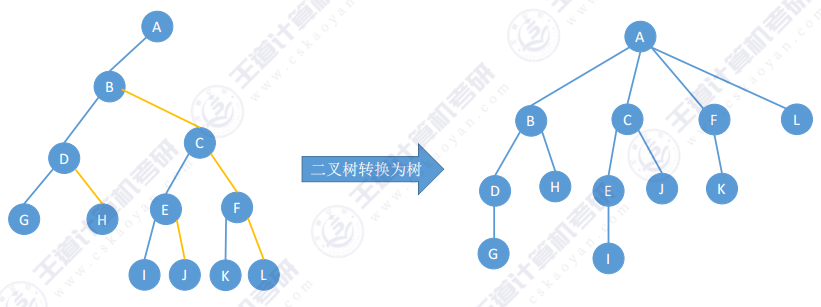
2.3 二叉树转树
- 二叉树转树技巧 :先画出树的根节点,从树的根节点开始,再按"树的层序"恢复每个结点的孩子
- 如何恢复一个结点的孩子 :在二叉树中,如果当前处理的结点有左孩子,就把左孩子和"一整串右指针糖葫芦"拆下来,按顺序挂在当前结点的下方
2.4 二叉树转森林
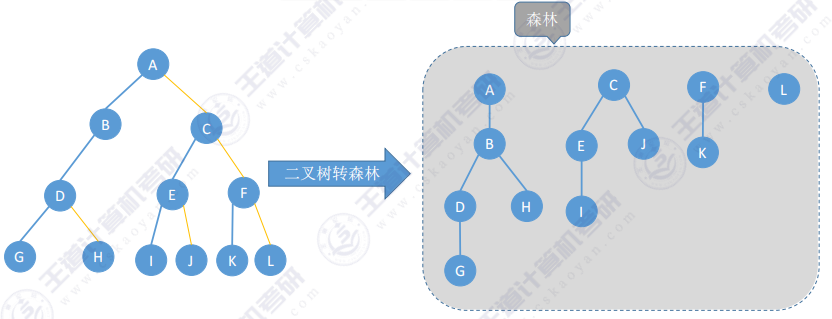
- 二叉树转森林技巧 :先把二叉树的根节点和"一整串右指针糖葫芦"拆下来,作为多棵树的根节点,再按"森林的层序"恢复每个结点的孩子
- 如何恢复一个结点的孩子:在二叉树中,如果当前处理的结点有左孩子,就把左孩子和"一整串右指针糖葫芦"拆下来,按顺序挂在当前结点的下方
2.5 总结
三、树和森林的遍历
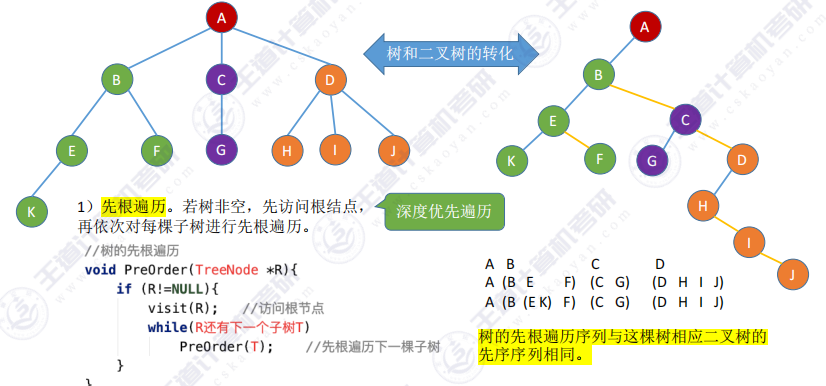
3.1 树的遍历
-
先根遍历 :树的先根遍历序列与这棵树相应二叉树的先序序列相同
-
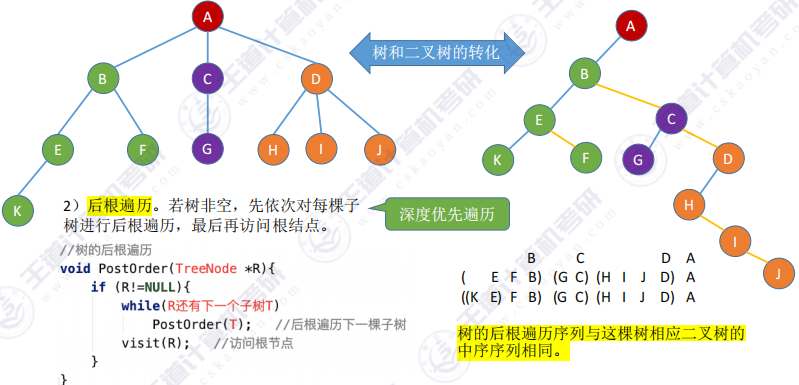
后根遍历 :树的后根遍历序列与这棵树相应二叉树的中序序列相同
-
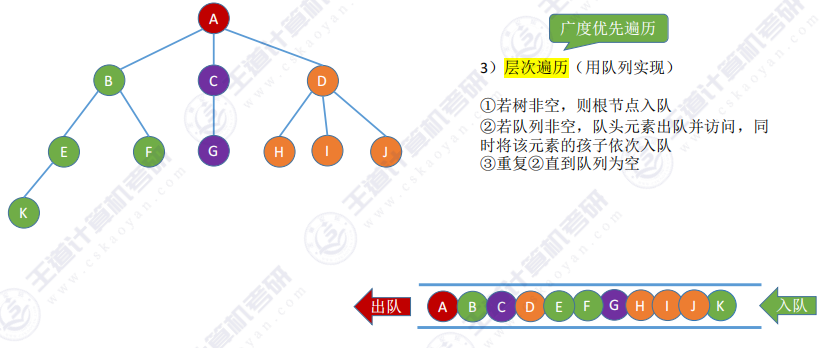
层序遍历 :用队列实现
3.2 森林的遍历
-
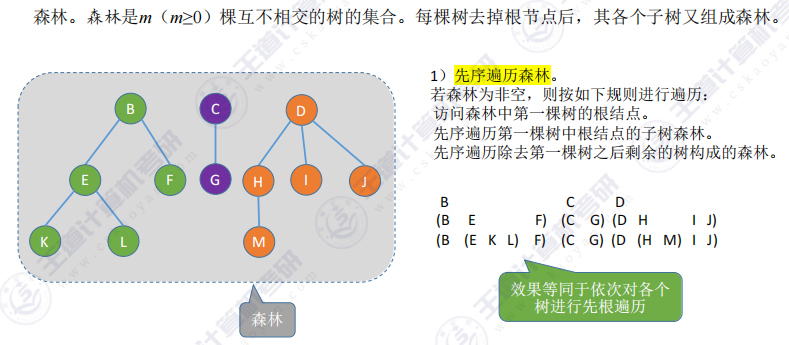
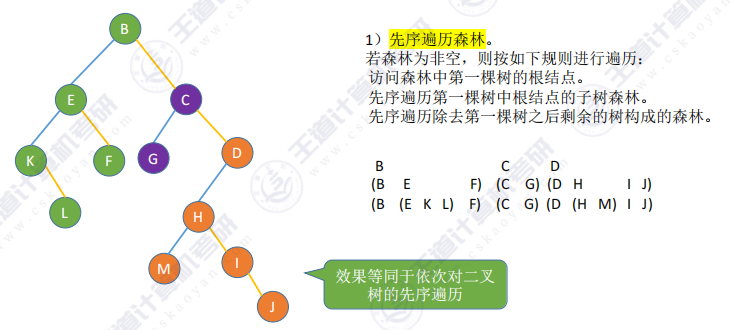
先序遍历
(1)效果等同于依次对各个树进行先根遍历;
(2)效果等同于依次对二叉树的先序遍历。
-
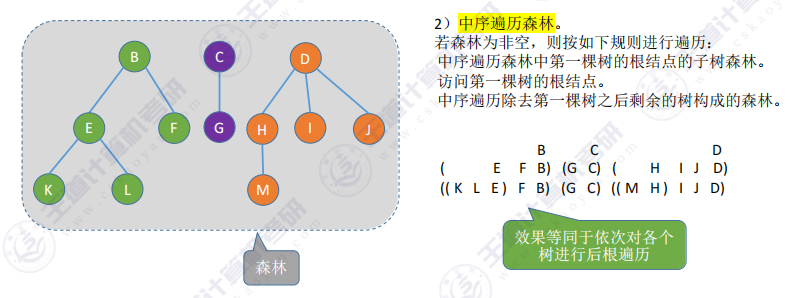
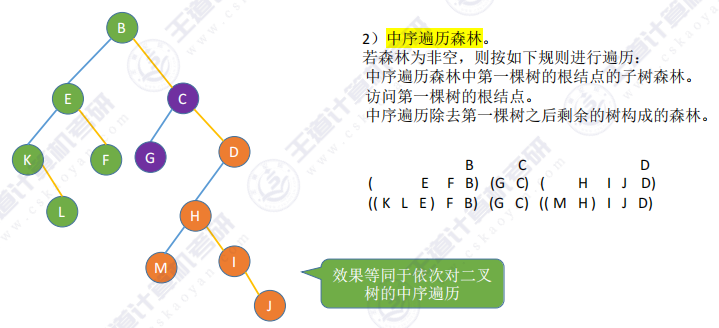
中序遍历
(1) 效果等同于依次对各个树进行后根遍历;
(2) 效果等同于依次对二叉树的中序遍历。
3.3 总结
