递归法:核心思路与实现
- 核心思路
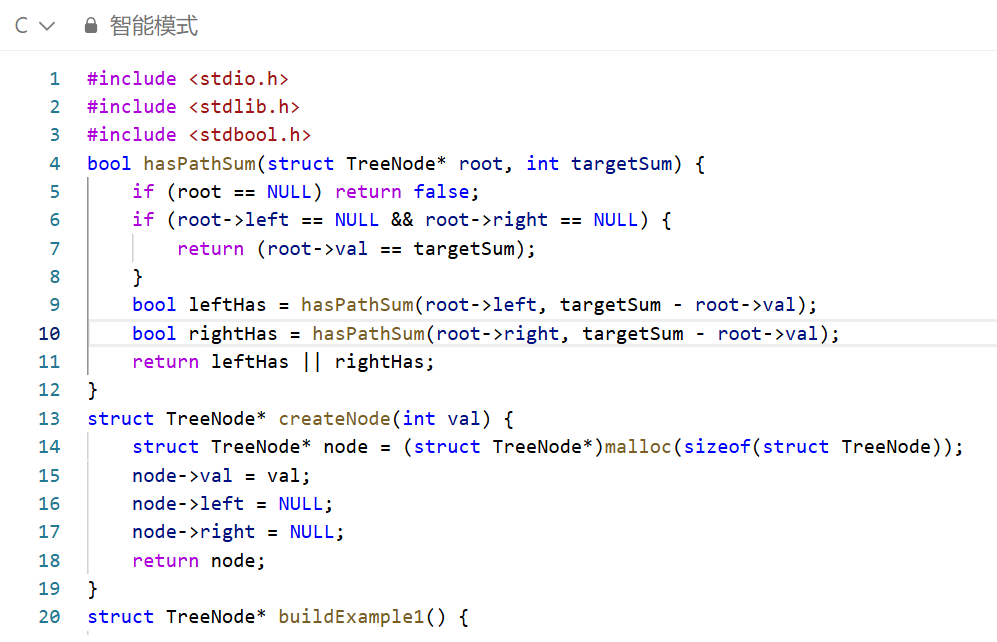
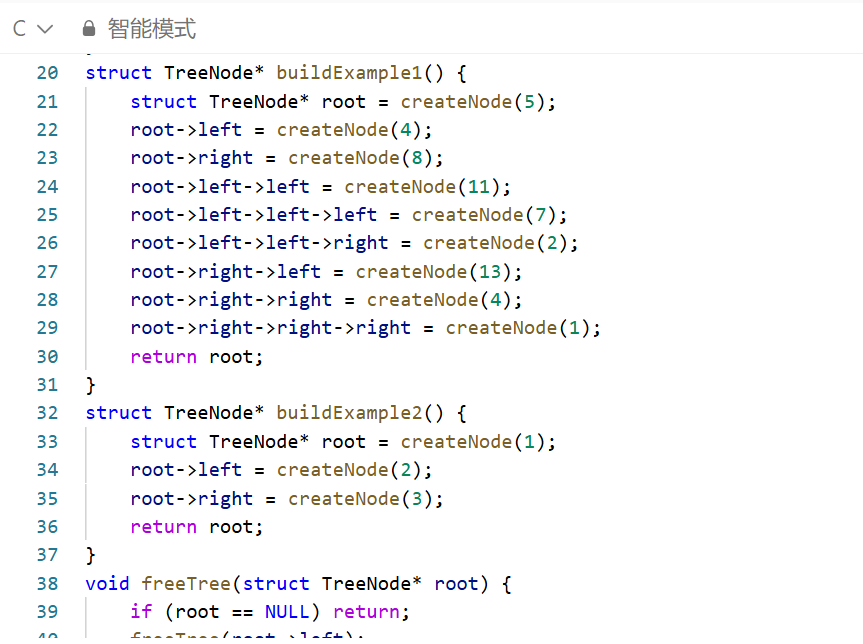
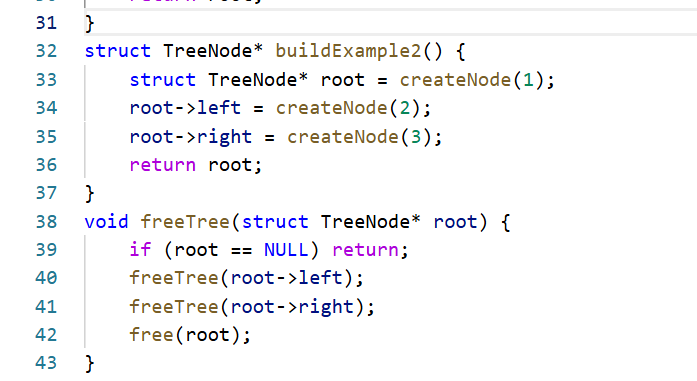
递归法的本质是将大问题分解为小问题,并利用函数调用栈来管理求解过程。
问题分解:要判断整棵树是否存在从根到叶的路径和为 targetSum,可以分解为:
判断根节点的左子树是否存在从左孩子到叶的路径和为 targetSum - root.val。
判断根节点的右子树是否存在从右孩子到叶的路径和为 targetSum - root.val。
终止条件:
如果当前节点为空(root == NULL),说明这条路走不通,返回 false。
如果当前节点是叶子节点(root->left == NULL && root->right == NULL),我们检查 root->val 是否等于当前剩余的目标和。如果相等,返回 true,否则返回 false。
递归过程:对于非叶子节点,递归地探索其左、右子树。只要左、右子树中有一个返回 true,就说明存在满足条件的路径。
 3. 优点
3. 优点
代码简洁直观:递归法的代码非常短,逻辑直接映射了问题的自然描述,易于理解和编写。
可读性强:代码本身就解释了算法的思路,几乎不需要额外的注释。
- 复杂度分析
时间复杂度: O (n)其中 n 是二叉树的节点总数。在最坏的情况下,我们需要访问树中的每一个节点才能确定是否存在满足条件的路径。空间复杂度: O (h)其中 h 是二叉树的高度。这是因为递归调用会在函数调用栈中保存帧。栈的最大深度取决于树的高度。在平衡二叉树中,高度 h 约为 log(n),空间复杂度相对较低。在最坏情况(例如,一棵退化成链表的树),高度 h 等于 n,此时空间复杂度为 O(n),可能会导致栈溢出。