深度学习基础知识总结（二）：激活函数（Activation Function）详解

在上一篇文章中，我们详细讲解了卷积（Convolution）的基本原理，知道了它如何从图像中提取出边缘、纹理、形状等特征。
但如果神经网络中只有卷积层和线性运算，那无论堆叠多少层，它本质上仍然是一个"线性模型"。

这样的网络------只能画直线，不能画曲线。

而现实世界是非线性的：

猫的图像和狗的图像差别不是像素线性组合能表达的；
声音、文本、视频等复杂数据中存在大量非线性特征；
深度学习的强大之处，就在于它能自动捕捉这些非线性模式。

所以，我们需要一个"让网络弯起来"的工具------

这就是 激活函数（Activation Function）。

一、为什么要用激活函数？

我们先看一个没有激活函数的网络：

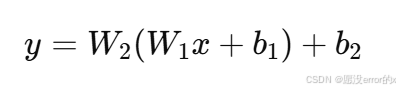
如果我们展开，会发现这是一个线性变换：

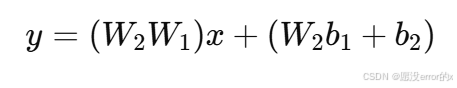
换句话说，两个线性层叠加起来依旧是一个线性函数。

那三层、十层、甚至一百层呢？

------没错，还是线性函数。

没有激活函数的神经网络 = 再深也学不会复杂的函数。

激活函数的引入，使网络具备"非线性拟合能力"，能学习图像、语言、语音等复杂关系。

它让神经网络从"直线大脑"进化成"曲线大脑"。

二、激活函数的作用总结

激活函数主要起以下三个作用：

引入非线性特征：让网络能拟合复杂的函数关系。
限制输出范围：防止数值爆炸，提高稳定性。
提供梯度：便于反向传播（求导更新参数）。

在神经网络中，每个神经元的计算可写为：

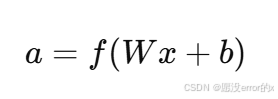
其中**f(⋅)**就是激活函数。

三、常见激活函数详解

1️⃣ Sigmoid 函数

公式：

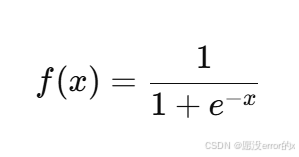
特点：

输出范围：(0,1)(0, 1)(0,1)
形状：S 形曲线，输入越大输出越接近 1，输入越小输出越接近 0。
常用于二分类问题的输出层。

优点：

具有概率意义：输出可以被解释为"属于正类的概率"。
平滑且单调。

缺点：

当输入过大或过小时，梯度接近 0，容易出现梯度消失。
输出非零均值，训练收敛慢。
计算较复杂（需要指数运算）。

📊 直观理解：

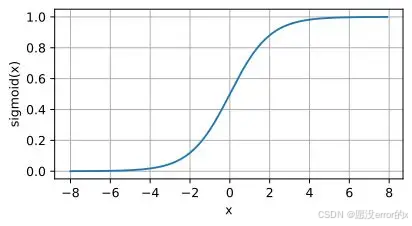
Sigmoid 就像一个"压缩器"，把任意数值压到 0～1 之间。

但压得太狠了，信息会"卡住"，导致网络更新慢。

2️⃣ Tanh（双曲正切函数）

公式：

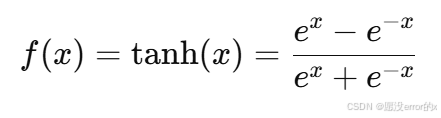
特点：

输出范围：(−1,1)(-1, 1)(−1,1)
零均值输出，收敛速度比 Sigmoid 更快。

优点：

能保留输入的符号信息（正负）；
相对 Sigmoid，不会导致神经元全部输出正值。

缺点：

同样存在梯度消失问题（在 ∣x∣>2|x| > 2∣x∣>2 区域梯度趋近 0）。

📈 直觉类比：

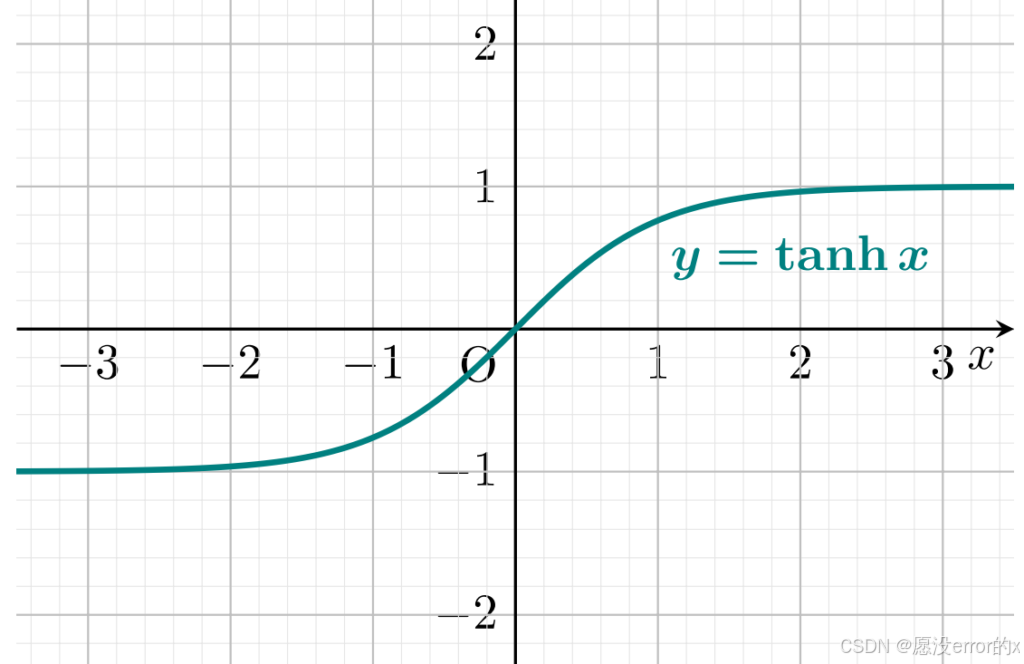
Tanh 就像 Sigmoid 的"升级版"------它让输出可以为负数，信息分布更平衡。

在早期 RNN 网络（如 LSTM）中非常常见。

3️⃣ ReLU（Rectified Linear Unit）

公式：

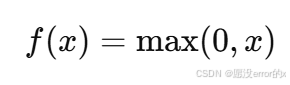
特点：

当 x>0：输出等于输入；
当 x≤0：输出为 0。
输出范围：[0, +∞)

优点：

计算简单；
不存在指数运算；
梯度恒为 1，不会梯度消失（在正区间）；
能加速收敛，使网络更稀疏（部分神经元输出 0）。

缺点：

当输入为负时梯度为 0，神经元可能"死掉"（即永远输出 0）。

📘 形象理解：

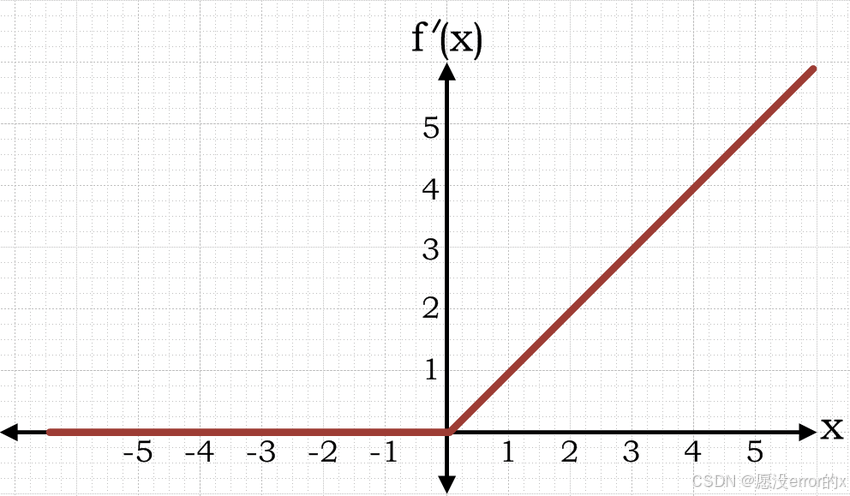
ReLU 就像一个"单向阀门"------只让正信号通过，负信号一律屏蔽。

这既加快了计算，又保留了有意义的激活。

💡 应用场景：

目前几乎所有 CNN、Transformer 的隐藏层都默认使用 ReLU。

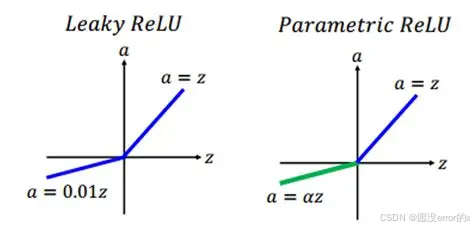
4️⃣ Leaky ReLU / Parametric ReLU

公式：

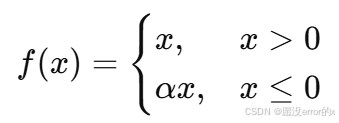
其中 α 通常取 0.01，或者作为可学习参数（PReLU）。

特点：

改进 ReLU 的"神经元死亡"问题；
让负区间也有微弱梯度，不完全丢弃信息。

使用建议：

当发现训练中大量神经元输出恒为 0 时，试试 Leaky ReLU；
PReLU 在轻量化网络中（如 MobileNet）常见。

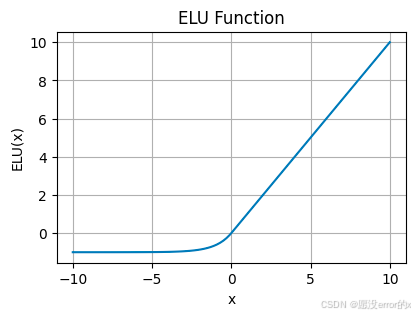
5️⃣ ELU / SELU（指数线性单元）

ELU 公式：

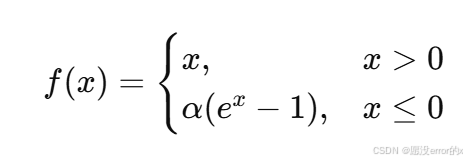
特点：

负区间平滑过渡，输出有负值；
输出均值更接近 0；
训练稳定性较好。

SELU 是在 ELU 基础上添加自归一化特性，用于特定网络结构（Self-Normalizing NN）。

6️⃣ Swish / GELU（现代激活函数）

Swish（Google 提出）：

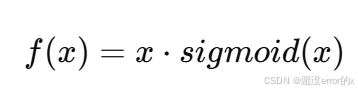
GELU（Gaussian Error Linear Unit）：

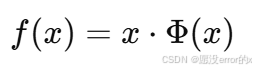
（Φ(x) 为高斯分布的累积分布函数）

特点：

平滑且可微；
在 Transformer、BERT 等大型模型中普遍使用；
表现往往优于 ReLU。

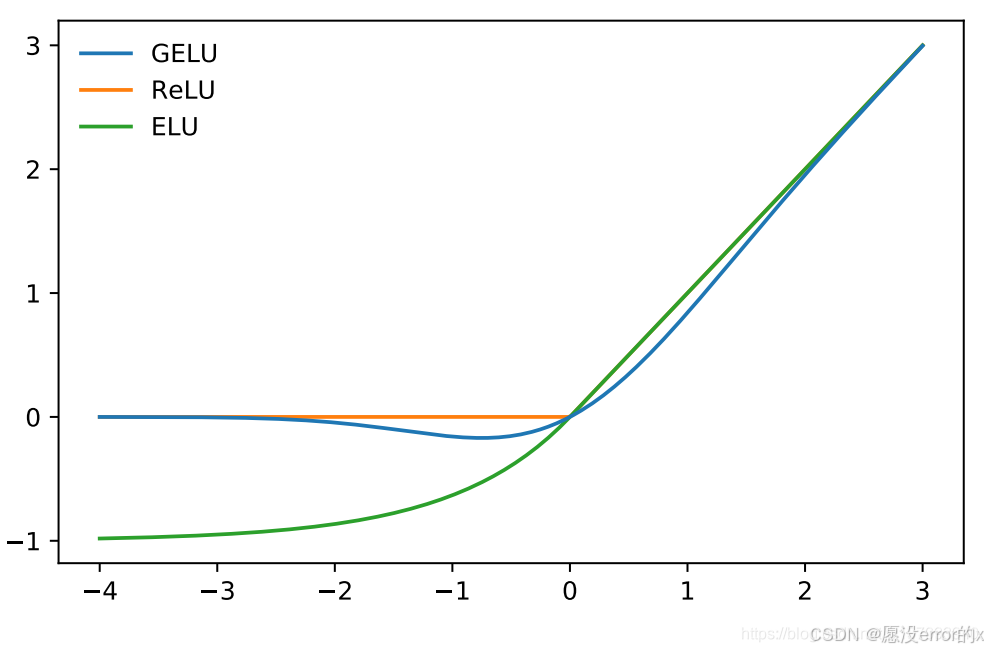
📊 理解：

Swish / GELU 可以看作是"带柔性阀门的 ReLU"------比 ReLU 更细腻，梯度流动更平滑。

四、激活函数之间的对比

激活函数	输出范围	零均值	是否有梯度消失	是否稀疏	常见用途
Sigmoid	(0, 1)	否	是	否	二分类输出层
Tanh	(-1, 1)	是	是	否	RNN 隐藏层
ReLU	[0, ∞)	否	否（正区间）	是	CNN 隐藏层
Leaky ReLU	(-∞, ∞)	是	否	稍弱	改进 ReLU
ELU	(-α, ∞)	近似	否	否	深层网络
Swish / GELU	(-∞, ∞)	是	否	否	Transformer / BERT 等

五、如何选择合适的激活函数？

✅ 经验总结：

场景	推荐激活函数
卷积神经网络（CNN）	ReLU / Leaky ReLU
深层网络（梯度稳定）	ELU / GELU
RNN / LSTM 网络	Tanh / Sigmoid
二分类输出层	Sigmoid
多分类输出层	Softmax
大模型（Transformer 等）	GELU / Swish

六、激活函数的可视化与代码实践

我们可以用 Python 简单绘制几种激活函数的曲线来直观感受差异 👇

复制代码

import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt

x = torch.linspace(-5, 5, 200)

activations = {
    "Sigmoid": torch.sigmoid(x),
    "Tanh": torch.tanh(x),
    "ReLU": F.relu(x),
    "Leaky ReLU": F.leaky_relu(x, 0.1),
    "Swish": x * torch.sigmoid(x)
}

plt.figure(figsize=(10,6))
for name, y in activations.items():
    plt.plot(x, y, label=name)
plt.legend()
plt.title("常见激活函数曲线对比")
plt.xlabel("x")
plt.ylabel("f(x)")
plt.grid(True)
plt.show()

运行后你会看到：

Sigmoid、Tanh 在两端趋于饱和；
ReLU 线性且稀疏；
Swish/GELU 更平滑。

七、总结

模块	作用
卷积层（Convolution）	提取局部特征
激活函数（Activation）	引入非线性，增加表达能力
池化层（Pooling）	降维，增强鲁棒性

激活函数虽然只是网络中的"一行代码"，

却决定了整个网络是否能"思考"。

一个恰当的激活函数，往往能显著提升模型的训练效率和性能。

📚 下一篇预告：

深度学习基础知识总结（三）：池化层（Pooling）与特征下采样

我将深入解析最大池化、平均池化的区别，以及它们如何让模型更稳、更强。

有需要的可以点个关注哦！