目录
[1. 代码逐行分析](#1. 代码逐行分析)
[2. 广播(Broadcasting)详解](#2. 广播(Broadcasting)详解)
[2.1 什么是广播?](#2.1 什么是广播?)
[2.2 广播规则](#2.2 广播规则)
[2.3 本例的广播过程](#2.3 本例的广播过程)
[2.4 可视化广播过程](#2.4 可视化广播过程)
[2.特殊切片:arr[:, 1:3]](#2.特殊切片:arr[:, 1:3])
[1. 布尔索引 (Boolean Indexing)](#1. 布尔索引 (Boolean Indexing))
[2. 条件筛选与替换](#2. 条件筛选与替换)
一、NumPy数值分析库基础架构
1、核心概念
NumPy(Numerical Python)是Python科学计算的基础库,提供高效的多维数组对象ndarray及配套工具集。其核心优势包括:
-
向量化运算:通过C语言优化的底层实现,消除Python循环的性能瓶颈
-
多维数组支持:统一处理标量、向量、矩阵及高阶张量
-
广播机制:实现不同形状数组间的自动维度扩展与运算对齐
-
内存连续存储:采用紧凑的C风格内存布局,提升数据访问效率
2、数组对象特性
-
数据类型系统:支持8/16/32/64位整数、单/双精度浮点、复数、布尔值等21种数据类型
-
维度属性 :通过
ndim(维度数)、shape(各维度大小)、size(元素总数)描述数组结构 -
字节序控制 :可指定大端序(>)或小端序(<)存储格式
3、广播机制详解
广播遵循三个核心规则:
-
维度对齐:从右向左逐维度匹配,缺失维度视为1
-
形状兼容:对应维度或为1或相等
-
扩展执行:维度为1的数组沿该方向复制至匹配大小
示例:
python
import numpy as np
a = np.array([[1, 2, 3]]) # shape (1,3)
b = np.array([4, 5, 6]) # shape (3,)
result = a + b 1. 代码逐行分析
python
import numpy as np作用 :导入NumPy库并设置别名为np,这样我们就可以用np.来调用NumPy的功能。
python
a = np.array([[1, 2, 3]]) # shape (1,3)作用:创建一个二维数组
-
[[1, 2, 3]]表示一个包含单个元素的列表,这个元素本身是列表[1, 2, 3] -
形状(shape) :
(1, 3)- 1行3列 -
可视化:a = [[1, 2, 3]]
python
b = np.array([4, 5, 6]) # shape (3,)作用:创建一个一维数组
-
[4, 5, 6]是一个普通的一维列表 -
形状(shape) :
(3,)- 只有3个元素,没有行和列的概念 -
可视化:b = [4, 5, 6]
python
result = a + b # 广播发生在这里!作用:执行数组加法,触发广播机制
2. 广播(Broadcasting)详解
2.1 什么是广播?
广播 是NumPy的一种智能扩展机制,允许不同形状的数组进行数学运算。NumPy会自动将较小的数组"广播"到较大数组的形状,使它们具有兼容的形状。
2.2 广播规则
NumPy从最右边的维度开始比较形状,遵循以下规则:
-
维度相等:可以运算
-
其中一个维度为1:可以广播扩展
-
其中一个维度缺失:可以广播扩展
-
其他情况:报错
2.3 本例的广播过程
python
a形状: (1, 3) # 1行3列
b形状: (3,) # 只有3个元素的一维数组
# 步骤1:维度对齐(从右向左比较)
a: (1, 3)
b: (3) # 在左边补1,变成(1, 3)
# 步骤2:扩展维度为1的轴
a: (1, 3) → 保持不变
b: (1, 3) → 将第0维(值为1)扩展到与a相同
# 实际扩展过程:
b = [4, 5, 6] 原始形状(3,)
扩展为:[[4, 5, 6]] 形状(1, 3)2.4 可视化广播过程
运算前:
python
a = [[1, 2, 3]] 形状(1,3)
b = [4, 5, 6] 形状(3,)广播后:
python
a = [[1, 2, 3]] 形状(1,3)
b = [[4, 5, 6]] 形状(1,3) ← b被扩展了!计算结果:
python
result = [[1+4, 2+5, 3+6]] = [[5, 7, 9]]
二、数组创建与运算体系
**1、**NumPy数组创建方法
1.常规创建
python
import numpy as np
# 从Python列表/元组创建
arr1 = np.array([1, 2, 3]) # 一维数组
arr2 = np.array([[1, 2, 3], [4, 5, 6]]) # 二维数组
arr3 = np.array([1, 2, 3], dtype=float) # 指定数据类型
print("常规创建:")
print(arr1) # [1 2 3]
print(arr2) # [[1 2 3] [4 5 6]]
print(arr3) # [1. 2. 3.] - 浮点数
应用场景:
-
将现有的Python数据转换为NumPy数组
-
需要精确控制数据类型时
-
小规模数据的手动创建
2.特殊值初始化
python
# 创建全零数组
zeros_1d = np.zeros(5) # 一维,5个元素
zeros_2d = np.zeros((2, 3)) # 二维,2行3列
# 创建全一数组
ones_1d = np.ones(4) # 一维,4个元素
ones_2d = np.ones((3, 2)) # 二维,3行2列
# 创建未初始化数组(内容随机)
empty_arr = np.empty((2, 2)) # 快速创建,不初始化
# 创建单位矩阵
identity = np.eye(3) # 3x3单位矩阵
print("\n特殊值初始化:")
print("zeros_2d:\n", zeros_2d)
print("ones_2d:\n", ones_2d)
应用场景:
-
预分配内存空间:知道数组大小但不知道具体值时
-
矩阵运算:单位矩阵用于线性代数
-
模板创建:创建与其他数组同形状的零/一数组
3.数值序列生成
python
# arange: 类似range,生成等差数列
arr_arange = np.arange(0, 10, 2) # [0, 2, 4, 6, 8]
# linspace: 生成指定数量的等间距数值
arr_linspace = np.linspace(0, 1, 5) # [0., 0.25, 0.5, 0.75, 1.]
# logspace: 生成对数等间距数值
arr_logspace = np.logspace(0, 2, 5) # [1., 3.16, 10., 31.62, 100.]
print("\n数值序列生成:")
print("arange:", arr_arange)
print("linspace:", arr_linspace)
print("logspace:", arr_logspace)
应用场景:
-
绘图坐标:创建x轴坐标点
-
采样点:在指定范围内均匀采样
-
数值模拟:创建时间序列或空间网格
4.随机数生成
python
# 均匀分布 [0,1)
uniform = np.random.rand(3, 3) # 3x3均匀分布
# 标准正态分布
normal = np.random.randn(3, 3) # 3x3标准正态分布
# 指定范围的随机整数
randint = np.random.randint(0, 100, (2, 4)) # 2x4,范围[0,100)
# 随机选择
choice = np.random.choice([1, 2, 3, 4], size=5) # 从列表中随机选择5次
#也就是:np.random.choice(
[1, 2, 3, 4], # 候选元素池:只能从这4个数字中选择
size=5 # 选择次数:总共选择5个元素
)
print("\n随机数生成:")
print("标准正态分布:\n", normal)
print("随机整数:\n", randint)
应用场景:
-
数据模拟:生成测试数据
-
机器学习:权重初始化
-
蒙特卡洛模拟:随机抽样
-
数据增强:添加随机噪声
5.综合对比表
| 方法类型 | 示例代码 | 主要参数 | 输出示例 | 应用场景 |
|---|---|---|---|---|
| 常规创建 | np.array([1,2,3]) |
Python列表, dtype | [1 2 3] |
数据转换 |
| 全零数组 | np.zeros((2,3)) |
shape | [[0. 0. 0.] [0. 0. 0.]] |
内存预分配 |
| 全一数组 | np.ones(5) |
shape | [1. 1. 1. 1. 1.] |
模板创建 |
| 数值序列 | np.arange(0,10,2) |
start, stop, step | [0 2 4 6 8] |
坐标生成 |
| 等分序列 | np.linspace(0,1,5) |
start, stop, num | [0. 0.25 0.5 0.75 1.] |
均匀采样 |
| 随机数组 | np.random.randn(3,3) |
shape | 标准正态分布 | 数据模拟 |
6.选择指南
-
已知具体数据 →
np.array() -
预分配空间 →
np.zeros()/np.ones() -
创建数值序列 →
np.arange()/np.linspace() -
生成随机数据 →
np.random相关函数 -
快速创建(不初始化) →
np.empty()
每种方法都有其特定的使用场景,根据实际需求选择最合适的方法!
2、运算体系分类
-
算术运算 :
+ - * / // % **(支持广播) -
矩阵运算 :
@或np.dot()实现矩阵乘法 -
逻辑运算 :
& | ^ ~(需配合括号使用) -
比较运算 :
== != > < >= <=返回布尔数组
3、数学计算实现
python
import numpy as np
# 1. 矩阵创建
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
print("矩阵 A:\n", A)
print("矩阵 B:\n", B)
# 2. 矩阵乘法
C = A @ B
print("\n矩阵乘法 A @ B:\n", C)
# 3. 矩阵求逆
A_inv = np.linalg.inv(A)
print("\nA的逆矩阵:\n", A_inv)
# 验证逆矩阵
identity = A @ A_inv
print("\n验证 A × A⁻¹:\n", identity)
# 4. 特征值分解
eigenvalues, eigenvectors = np.linalg.eig(A)
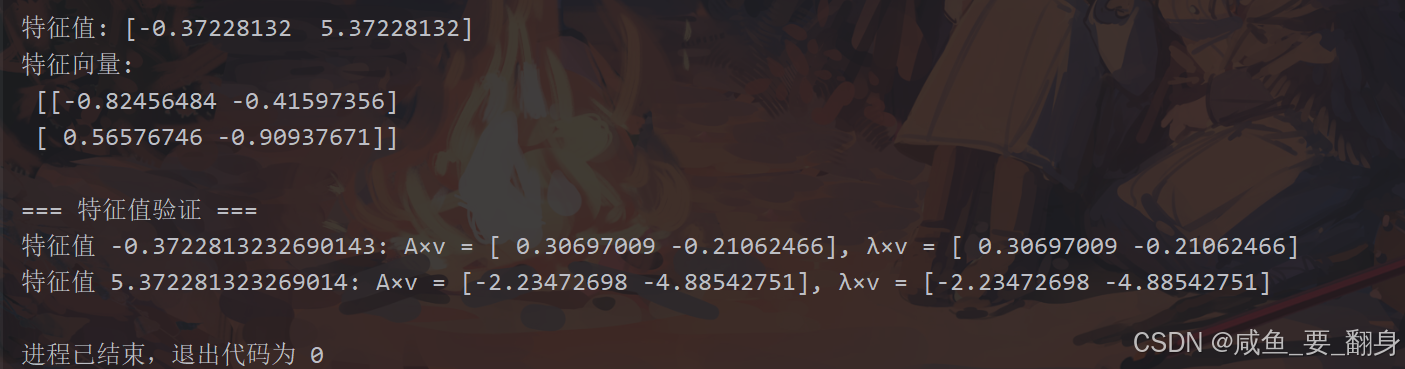
print("\n特征值:", eigenvalues)
print("特征向量:\n", eigenvectors)
# 验证特征值分解
print("\n=== 特征值验证 ===")
for i in range(len(eigenvalues)):
λ = eigenvalues[i]
v = eigenvectors[:, i]
print(f"特征值 {λ}: A×v = {A@v}, λ×v = {λ*v}")
三、高级索引与数据筛选技术
1、索引机制
-
基本索引 :
arr[i,j]形式访问元素 -
花式索引:使用整数数组或列表进行非连续访问
python
arr = np.array([10,20,30,40,50])
print(arr[[1,3,4]]) # 输出 [20 40 50]从数组 arr 中按索引 [1, 3, 4] 的顺序提取对应的元素。
2、切片操作
-
支持多维切片:
arr[start:stop:step, ...] -
特殊切片:
arr[:,1:3]选取所有行的第2-3列
1.二维数组切片示例
python
import numpy as np
# 创建 4x5 的二维数组
arr = np.array([[1, 2, 3, 4, 5],
[6, 7, 8, 9, 10],
[11,12,13,14,15],
[16,17,18,19,20]])
print("原始数组:")
print(arr)
print("形状:", arr.shape) # (4, 5)
2.特殊切片:arr[:, 1:3]
python
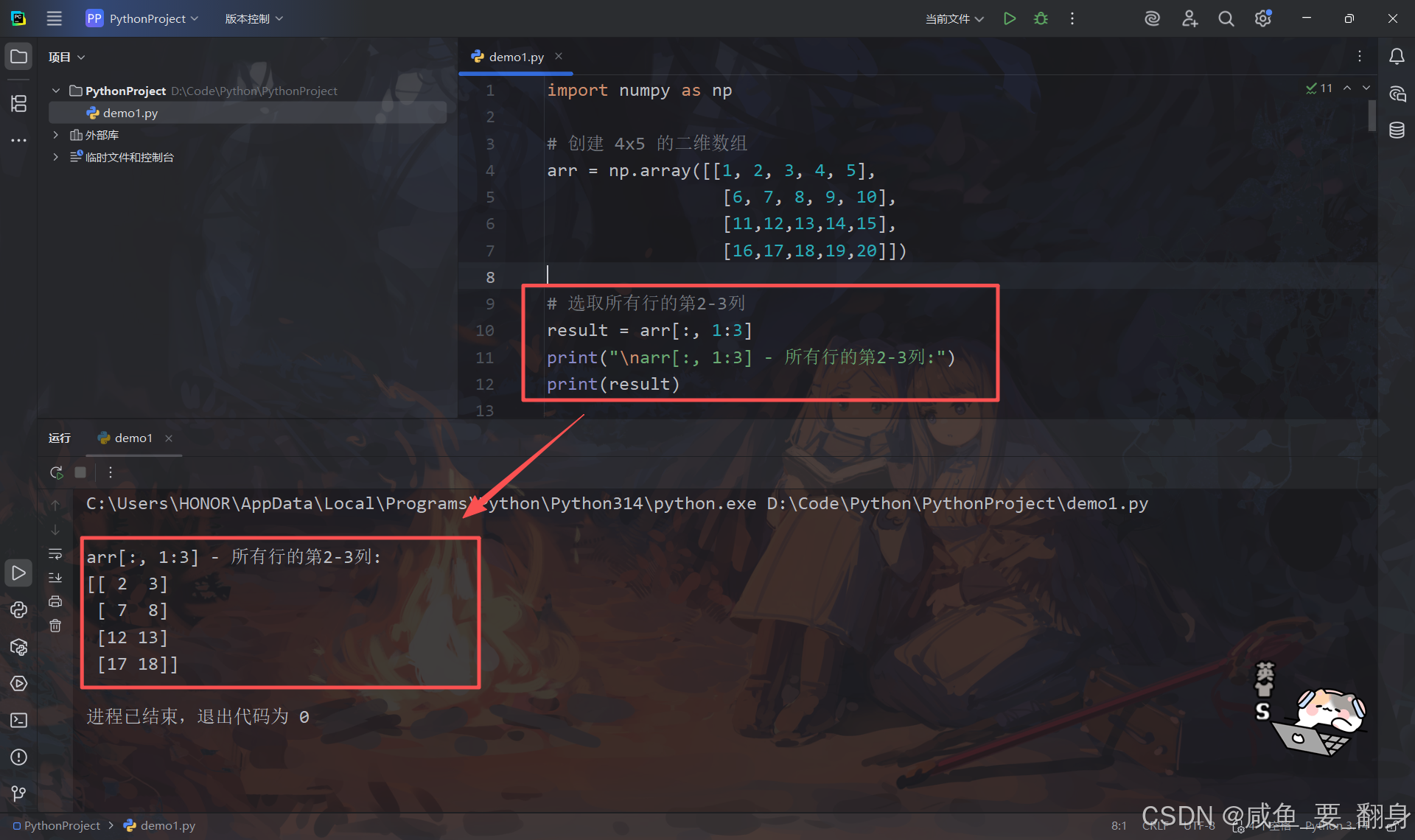
# 选取所有行的第2-3列
result = arr[:, 1:3]
print("\narr[:, 1:3] - 所有行的第2-3列:")
print(result)解析:
-
:→ 所有行(第0维:行) -
1:3→ 第2列到第3列(索引1到2,不包含3)
结果:
3、布尔索引
1. 布尔索引 (Boolean Indexing)
python
data = np.random.randn(5,5) # 创建5x5的随机数组
mask = data > 0 # 生成布尔掩码
positive_data = data[mask] # 提取所有正数工作原理:
-
data > 0返回一个与原数组形状相同的布尔数组 -
True表示对应位置的元素满足条件(>0) -
data[mask]返回所有True位置对应的一维数组
示例演示
python
import numpy as np
# 创建一个3x3的数组(比5x5小,方便观察)
data = np.array([[ 1.2, -0.5, 0.8],
[-1.1, 2.3, -0.2],
[ 0.4, -0.9, 1.5]])
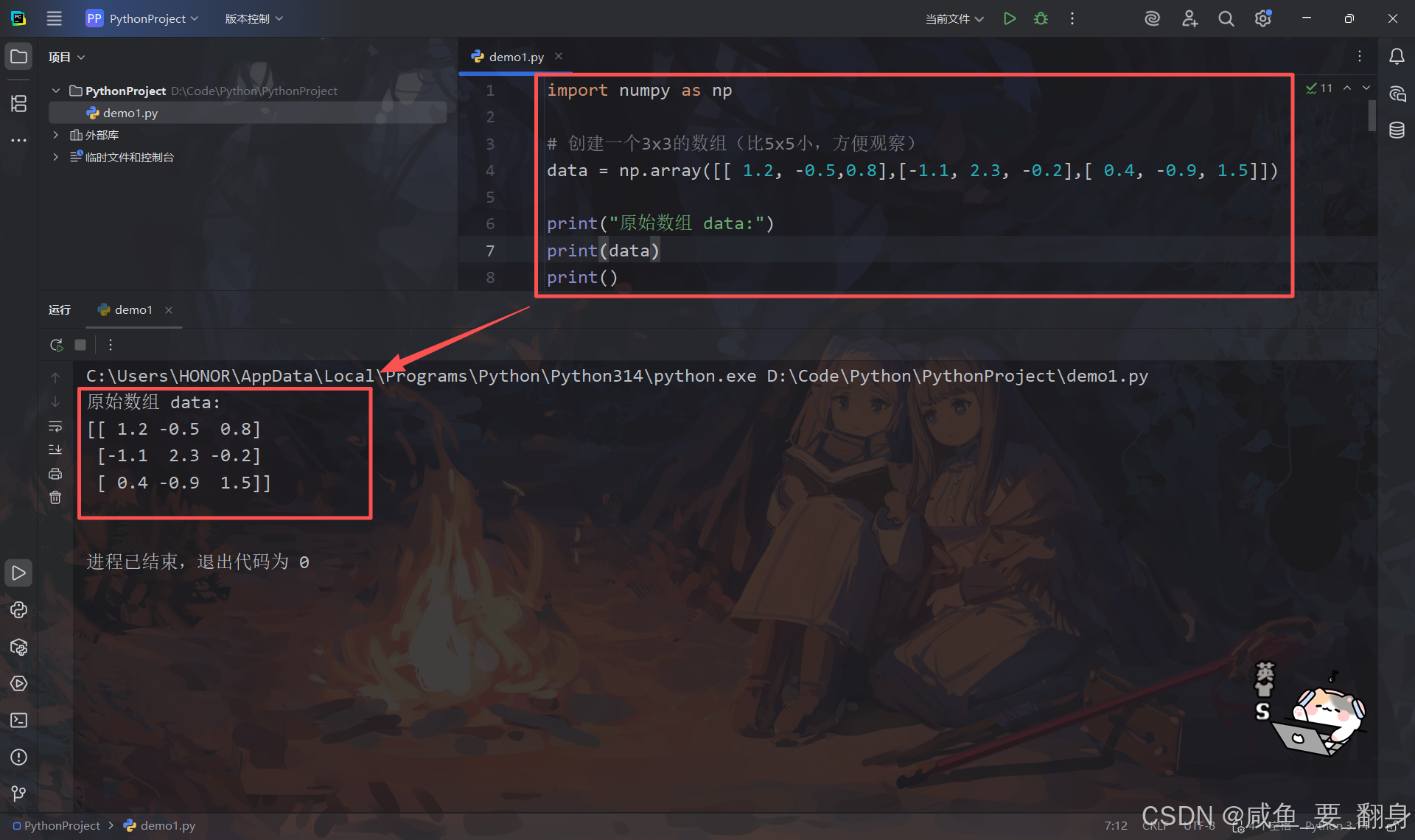
print("原始数组 data:")
print(data)
print()输出:
步骤1:生成布尔掩码
python
mask = data > 0
print("布尔掩码 mask (data > 0):")
print(mask)输出:
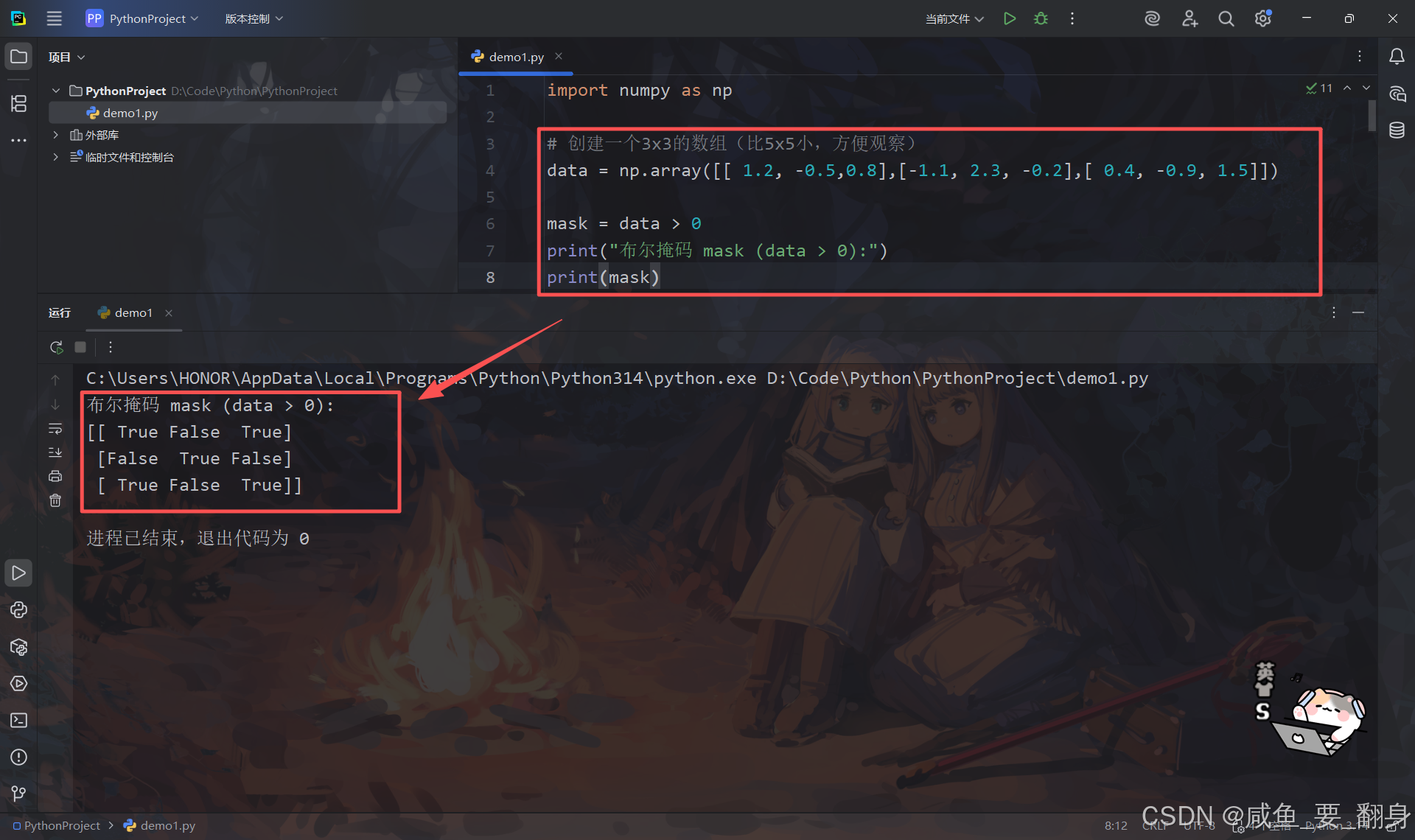
解释:
-
True表示该位置的数 > 0 -
False表示该位置的数 ≤ 0 -
掩码形状与data相同,都是3x3
步骤2:使用布尔掩码提取数据
python
positive_data = data[mask]
print("提取的正数 positive_data:")
print(positive_data)输出:
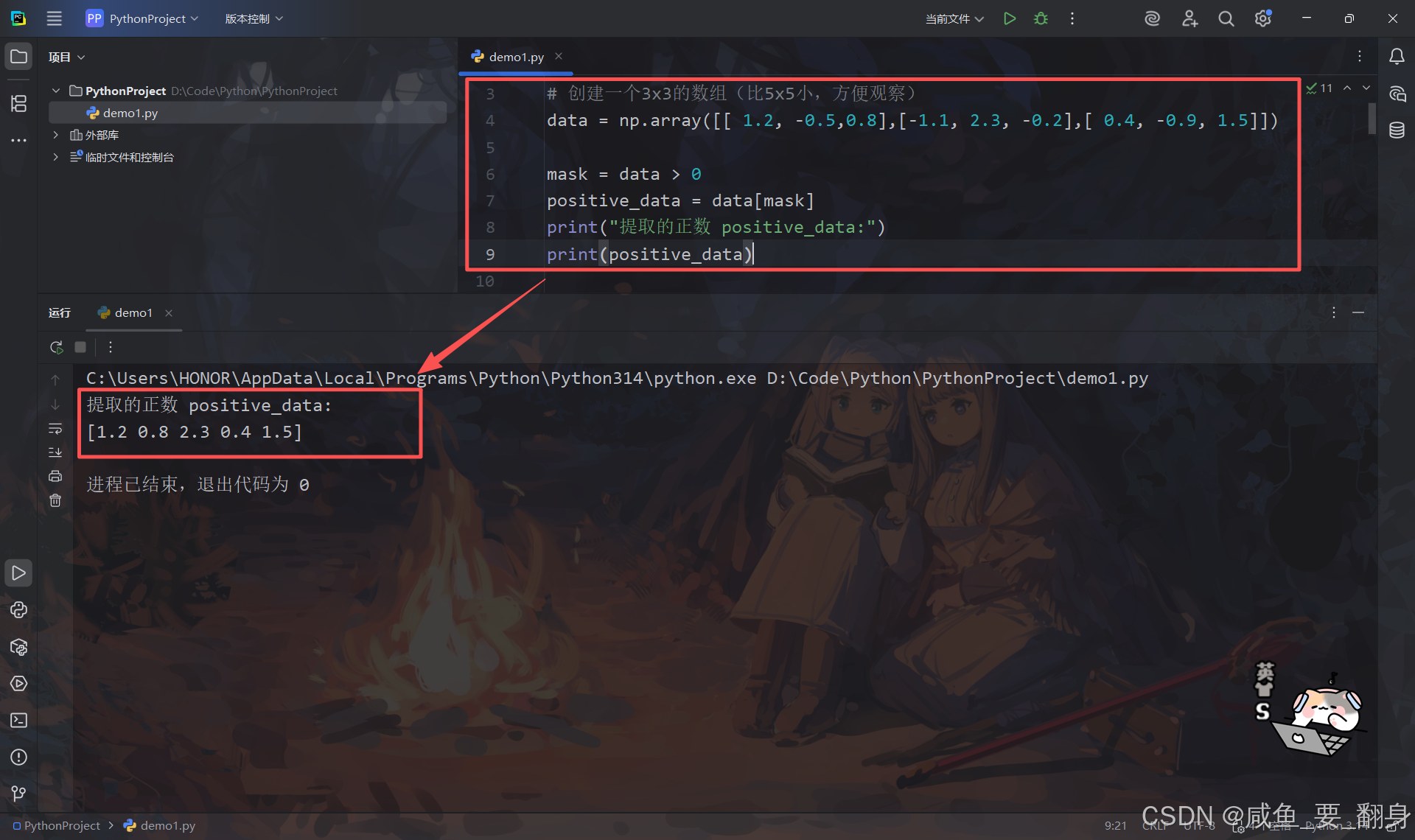
可视化理解
python
原始数组 data: 布尔掩码 mask: 提取结果:
[ 1.2, -0.5, 0.8] [ T, F, T] → 提取: 1.2, 0.8
[-1.1, 2.3, -0.2] [ F, T, F] → 提取: 2.3
[ 0.4, -0.9, 1.5] [ T, F, T] → 提取: 0.4, 1.5最终结果:
-
原始数组:3x3的二维数组
-
提取结果 :包含所有正数的一维数组
[1.2, 0.8, 2.3, 0.4, 1.5]
关键点:
-
布尔索引会"拍平"数组,返回一维结果
-
只保留掩码为
True位置的元素 -
顺序按行遍历(从左到右,从上到下)
2. 条件筛选与替换
步骤1:设置阈值并生成布尔掩码
python
threshold = 0.5
mask = data < threshold
print("布尔掩码 mask (data < 0.5):")
print(mask)输出:
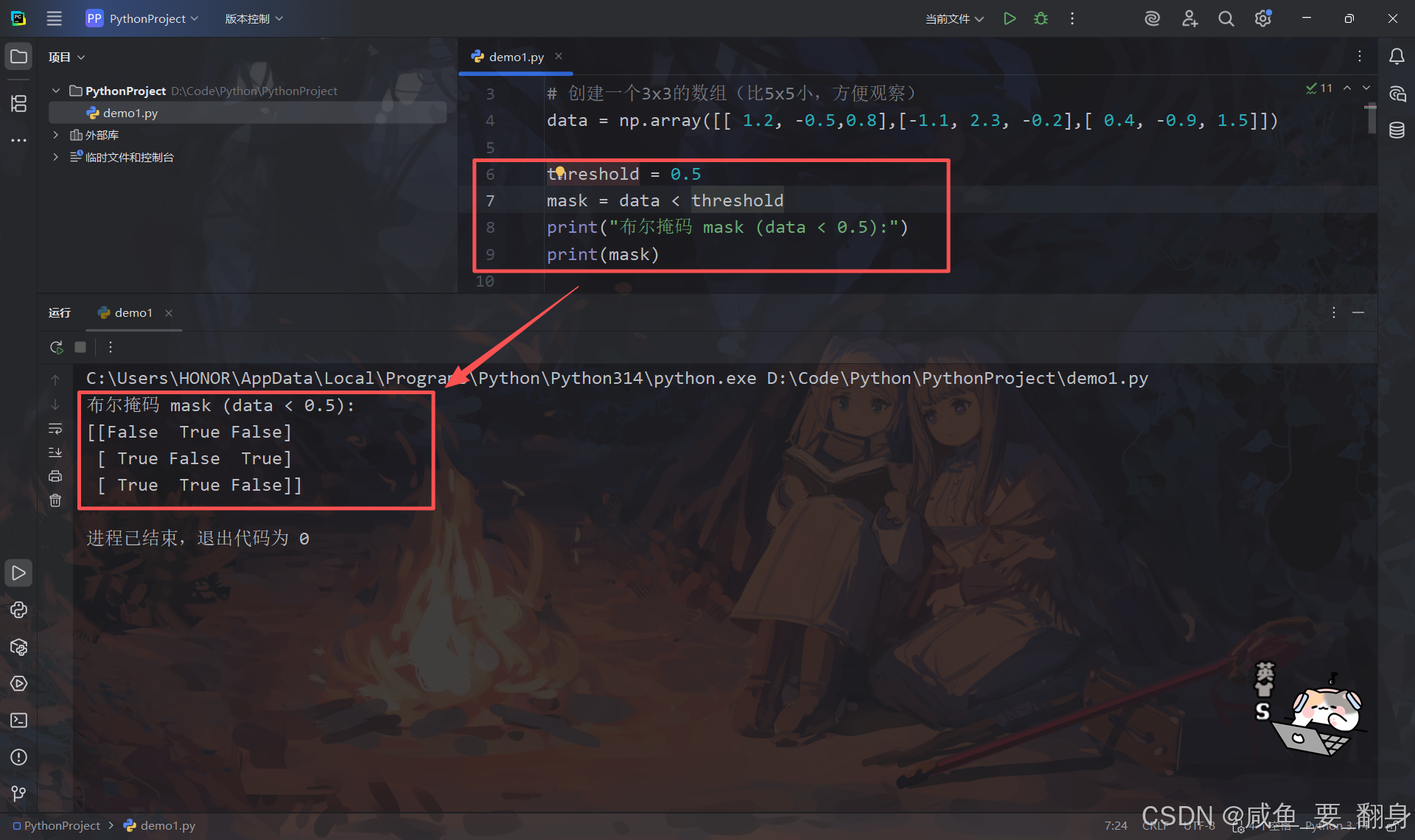
解释:
-
True表示该位置的数 < 0.5 -
False表示该位置的数 ≥ 0.5
步骤2:执行条件替换
python
data[data < threshold] = np.nan
print("替换后的数组 data:")
print(data)输出:
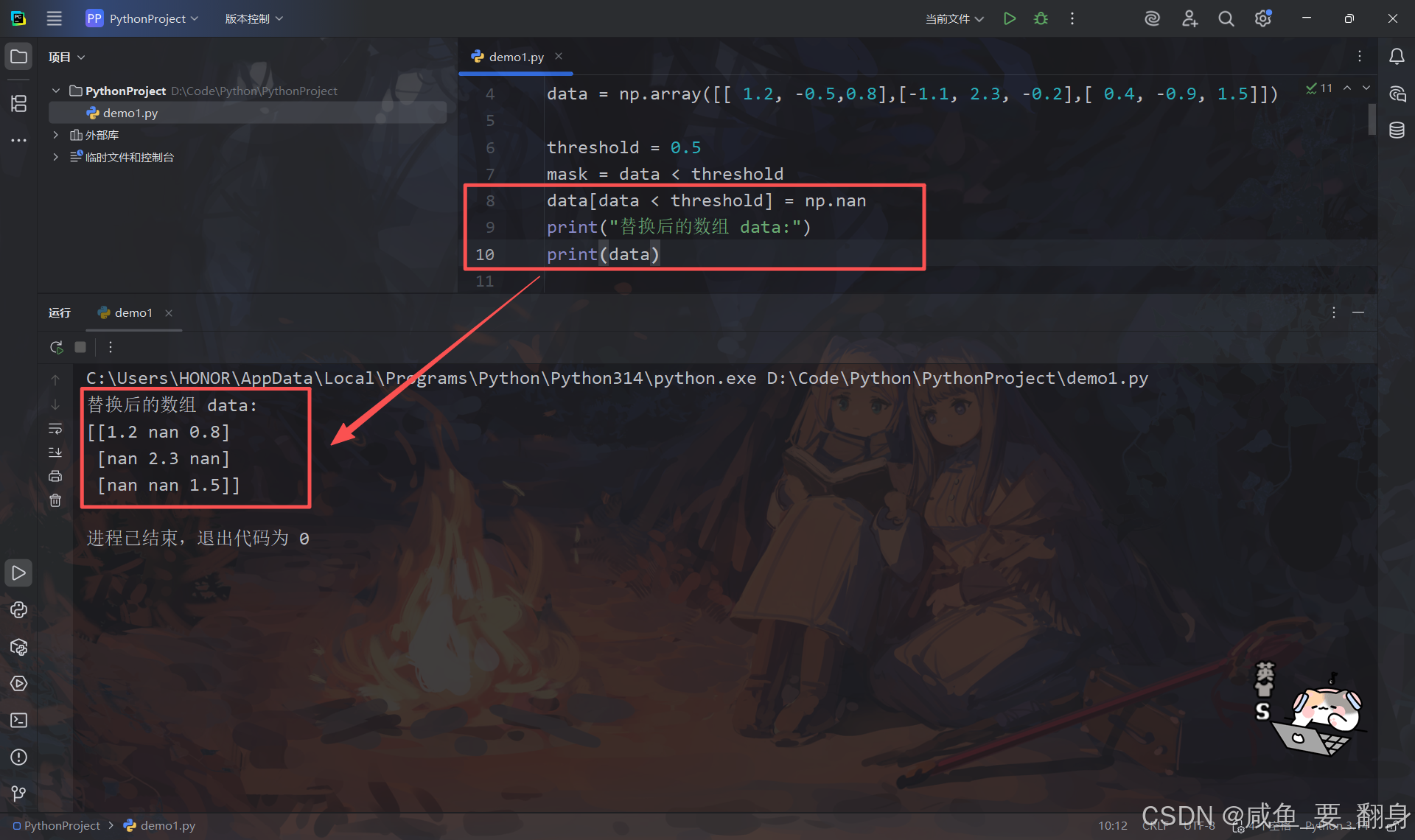
可视化理解
python
替换前: 条件判断: 替换后:
[ 1.2, 0.3, 0.8] [ F, T, F] [ 1.2, nan, 0.8]
[ 0.1, 2.3, 0.4] [ T, F, T] [ nan, 2.3, nan]
[ 0.6, -0.9, 1.5] [ F, T, F] [ 0.6, nan, 1.5]详细变化:
被替换的元素:
-
0.3→nan(因为 0.3 < 0.5) -
0.1→nan(因为 0.1 < 0.5) -
0.4→nan(因为 0.4 < 0.5) -
-0.9→nan(因为 -0.9 < 0.5)
保留的元素:
-
1.2(≥ 0.5) -
0.8(≥ 0.5) -
2.3(≥ 0.5) -
0.6(≥ 0.5) -
1.5(≥ 0.5)
工作原理:
-
data < threshold生成布尔掩码 -
直接将满足条件的元素替换为
np.nan -
这是一种原地操作,会修改原数组
主要特点:
-
高效:向量化操作,比循环快得多
-
简洁:一行代码完成复杂筛选
-
灵活 :可组合多个条件(使用
&,|,~) -
实用:常用于数据清洗和预处理
这两种方法在数据处理中非常常用,特别是数据清洗、异常值处理等场景。
四、特殊数值处理机制
1、特殊值定义
-
NaN(Not a Number):表示未定义或不可表示的数值 -
Inf(Infinity):表示超出浮点数表示范围的数值
2、生成方式
python
nan_val = np.nan
inf_val = np.inf
neg_inf = -np.inf3、影响分析
-
传播特性:任何涉及NaN的运算结果均为NaN
-
比较陷阱 :
NaN != NaN返回True -
统计影响 :
np.mean()等聚合函数默认忽略NaN
4、处理方法
1. 检测特殊值
python
np.isnan(arr) # 检测NaN值(不是数字)
np.isinf(arr) # 检测无穷大值(正无穷或负无穷)作用:
-
返回布尔数组,标记特殊值的位置
-
True表示该位置是特殊值,False表示正常值
2. 填充处理
python
arr_filled = np.nan_to_num(arr, nan=0.0, posinf=1e6, neginf=-1e6)参数含义:
-
nan=0.0:将所有NaN替换为0.0 -
posinf=1e6:将所有正无穷大替换为1000000 -
neginf=-1e6:将所有负无穷大替换为-1000000
3. 过滤处理
python
clean_data = arr[~np.isnan(arr)]解释:
-
np.isnan(arr):找出所有NaN位置 -
~:取反运算符,把True变False,False变True -
arr[~np.isnan(arr)]:只保留不是NaN的元素
简单示例:
python
import numpy as np
arr = np.array([1, 2, np.nan, 4, np.inf, -np.inf])
# 检测
print("NaN位置:", np.isnan(arr))
print("无穷大位置:", np.isinf(arr))
# 填充
filled = np.nan_to_num(arr, nan=0, posinf=999, neginf=-999)
print("填充后:", filled)
# 过滤
clean = arr[~np.isnan(arr)]
print("过滤NaN后:", clean)输出:
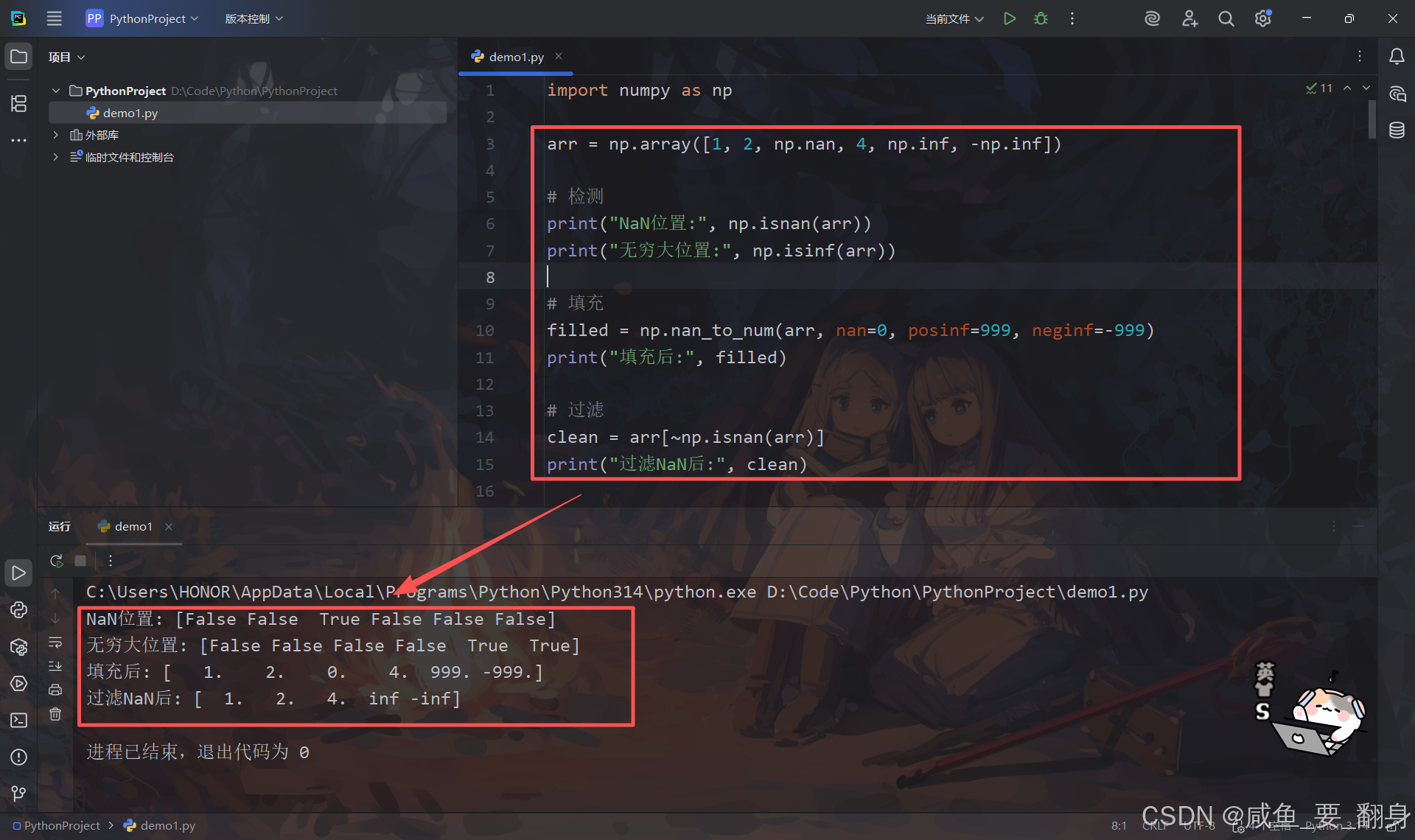
总结:
-
检测:找出问题数据
-
填充:用合理值替换特殊值
-
过滤:直接删除特殊值
五、函数应用体系
1、聚合函数
| 函数 | 功能说明 | 示例 |
|---|---|---|
np.sum() |
求和(可指定轴方向) | np.sum(arr, axis=1) |
np.mean() |
计算算术平均值 | np.mean(arr, keepdims=True) |
np.std() |
计算标准差 | np.std(arr, ddof=1) |
np.argmax() |
返回最大值索引 | np.argmax(arr, axis=0) |
1. np.sum() - 求和
python
np.sum(arr, axis=1) # 沿轴1(行方向)求和功能:计算数组元素的和
axis参数:
-
axis=0:按列求和(垂直方向) -
axis=1:按行求和(水平方向) -
不指定:计算所有元素的和
2. np.mean() - 求平均值
python
np.mean(arr, keepdims=True) # 计算平均值并保持维度功能:计算算术平均值
keepdims:保持原数组维度,结果维度不变
3. np.std() - 求标准差
python
np.std(arr, ddof=1) # 计算样本标准差功能:计算标准差,衡量数据离散程度
ddof参数:
-
ddof=0:总体标准差(默认) -
ddof=1:样本标准差
4. np.argmax() - 找最大值索引
python
np.argmax(arr, axis=0) # 沿轴0(列方向)找最大值索引功能:返回最大值所在的索引位置
axis参数:
-
axis=0:每列的最大值索引 -
axis=1:每行的最大值索引 -
不指定:整个数组的最大值索引(扁平化后)
2、逐元素函数
-
数学变换 :
np.exp(), np.log(), np.sqrt() -
三角函数 :
np.sin(), np.cos(), np.arctan2() -
舍入函数 :
np.round(), np.floor(), np.ceil()
3、高级应用示例
python
# 加权平均计算
weights = np.array([0.1, 0.3, 0.6])
data = np.array([1, 2, 3])
weighted_mean = np.sum(data * weights)
# 数据标准化
def normalize(arr):
return (arr - np.mean(arr)) / np.std(arr)