【C++ STL容器适配器】：解密Stack、Queue与Priority Queue的设计智慧

🎬 博主名称 ：月夜的风吹雨
🔥 个人专栏 : 《C语言》《基础数据结构》《C++入门到进阶》

⛺️任何一个伟大的思想，都有一个微不足道的开始!

一篇彻底讲清容器适配器原理、设计权衡与底层实现的深度教程 ✨

💬 前言

本文将带你深入STL容器适配器的核心设计，不仅理解"如何使用"，更要洞悉"为何如此设计"。我们将揭开这些看似简单却蕴含深意的组件背后的奥秘。

✨ 阅读后，你将彻底掌握：

容器适配器模式的本质与价值

stack、queue和priority_queue的接口设计哲学

deque作为底层容器的技术权衡

优先级队列与堆算法的完美融合

自定义实现STL组件的关键技巧

文章目录

[一、什么是容器适配器？ 🧩](#一、什么是容器适配器？ 🧩)
- [1.1 适配器模式的本质](#1.1 适配器模式的本质)
- [1.2 STL中的适配器](#1.2 STL中的适配器)
[二、Stack：后进先出的精妙实现 📚](#二、Stack：后进先出的精妙实现 📚)
- [2.1 Stack接口与使用场景](#2.1 Stack接口与使用场景)
- [2.2 例题：最小栈的实现](#2.2 例题：最小栈的实现)
- [2.3 例题：栈的弹出序列验证](#2.3 例题：栈的弹出序列验证)
[三、Queue：先进先出的可靠保障 🚶](#三、Queue：先进先出的可靠保障 🚶)
- [3.1 Queue接口与使用场景](#3.1 Queue接口与使用场景)
[四、Priority Queue：堆结构的STL封装 ⛰️](#四、Priority Queue：堆结构的STL封装 ⛰️)
- [4.1 Priority Queue的本质](#4.1 Priority Queue的本质)
- [4.2 接口与自定义比较器](#4.2 接口与自定义比较器)
- [4.3 例题：数组中第K个最大元素](#4.3 例题：数组中第K个最大元素)
五、为什么stack和queue选择deque作为默认容器？🔍
- [5.1 deque：分段连续的精妙设计](#5.1 deque：分段连续的精妙设计)
- [5.2 为何stack和queue选择deque？](#5.2 为何stack和queue选择deque？)
[六、模拟实现：stack、queue、priority_queue 💻](#六、模拟实现：stack、queue、priority_queue 💻)
- [6.1 Stack的模拟实现](#6.1 Stack的模拟实现)
- [6.2 Queue的模拟实现](#6.2 Queue的模拟实现)
- [6.3 Priority Queue的模拟实现](#6.3 Priority Queue的模拟实现)
[七、性能对比：不同场景下的容器选择 📊](#七、性能对比：不同场景下的容器选择 📊)
- [7.1 排序性能对比](#7.1 排序性能对比)
- [7.2 优化策略：deque排序的最佳实践](#7.2 优化策略：deque排序的最佳实践)
[八、思考与总结 ✨](#八、思考与总结 ✨)
九、下篇预告

一、什么是容器适配器？ 🧩

在深入具体容器前，我们需要理解"适配器"这一核心概念。

1.1 适配器模式的本质

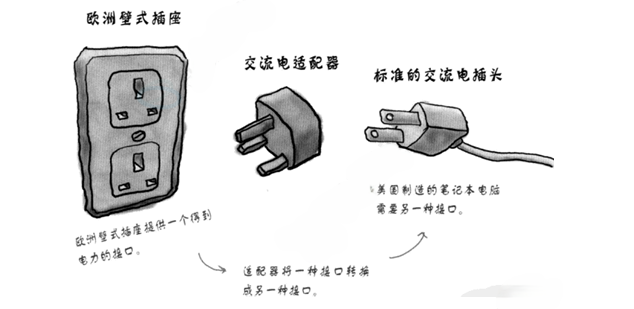
适配器模式（Adapter Pattern）是一种设计模式，它将一个类的接口转换成客户希望的另一个接口。

在电子设备中，适配器让不同标准的接口能够协作；在STL中，容器适配器让通用容器通过特定接口满足特定数据结构需求。

1.2 STL中的适配器

STL将stack、queue和priority_queue定义为容器适配器，而非独立容器，这种设计蕴含深意：

cpp 复制代码

template<class T, class Container = deque<T>>
class stack
{
    Container _con; // 底层容器
public:
    void push(const T& x) { _con.push_back(x); }
    void pop() { _con.pop_back(); }
    const T& top() const { return _con.back(); }
    // 其他接口...
};

💡 核心思想：

复用而非重复：基于现有容器构建新功能
接口隔离：只暴露特定操作，隐藏不必要的功能
策略可替换：底层容器可自定义，保持接口不变

适配器不是创造新轮子，而是将现有轮子改装成适合特定车辆的形态。

二、Stack：后进先出的精妙实现 📚

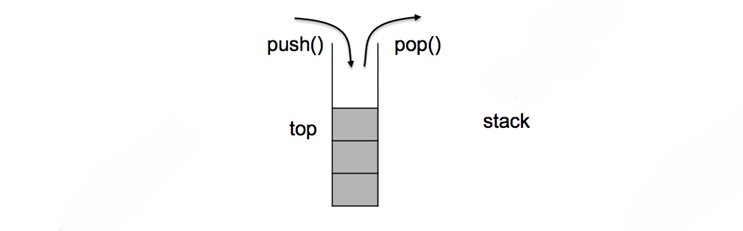
2.1 Stack接口与使用场景

STL stack提供简洁而精准的接口：

函数	说明
`stack()`	构造空栈
`empty()`	检测栈是否为空
`size()`	返回栈中元素个数
`top()`	返回栈顶元素引用
`push(x)`	将元素 x 压入栈中
`pop()`	弹出栈顶元素

应用场景：

函数调用栈
括号匹配
表达式求值（如逆波兰表达式）
深度优先搜索

2.2 例题：最小栈的实现

点击链接跳转 👉力扣：155. 最小栈

cpp 复制代码

class MinStack {
public:
    void push(int x) {
        _elem.push(x);
        // 如果x小于等于_min栈顶或_min为空，将x也压入_min
        if(_min.empty() || x <= _min.top())
            _min.push(x);
    }

    void pop() {
        // 如果弹出的元素等于_min栈顶，_min也要弹出
        if(_min.top() == _elem.top())
            _min.pop();
        _elem.pop();
    }

    int top() { return _elem.top(); }
    int getMin() { return _min.top(); }

private:
    stack<int> _elem;  // 保存栈中元素
    stack<int> _min;   // 保存当前最小值
};

💡 核心思路：

使用辅助栈记录历史最小值
入栈时同步更新两个栈
出栈时保持两个栈状态一致
O ( 1 ) O(1) O(1)时间复杂度获取最小值

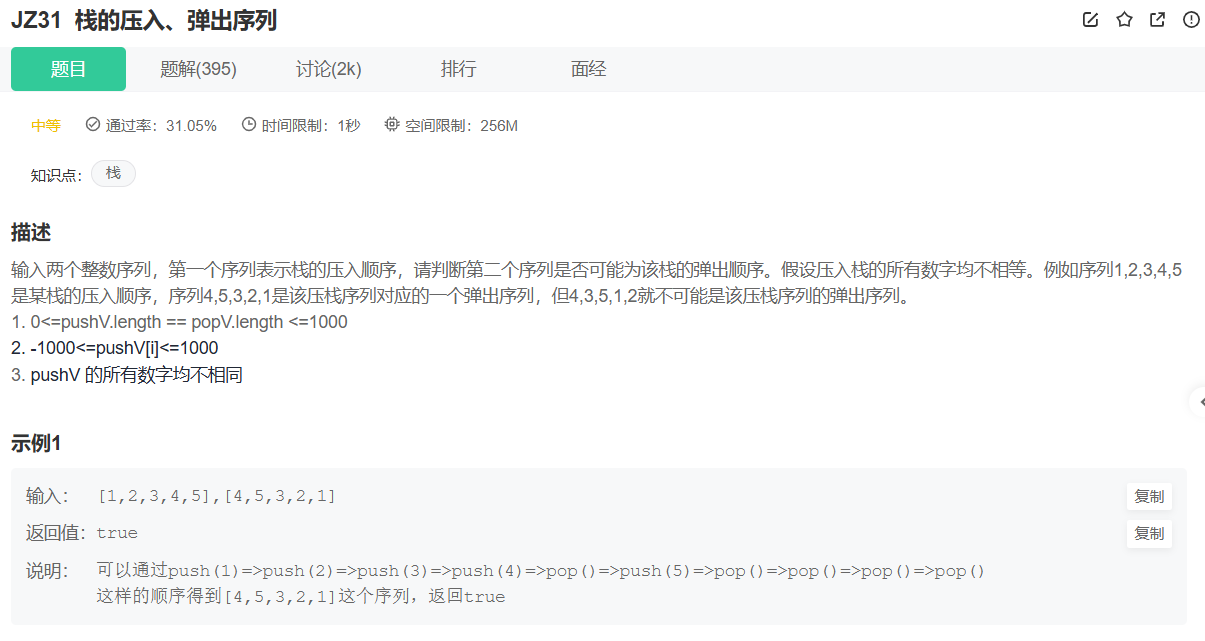
2.3 例题：栈的弹出序列验证

点击链接跳转 👉牛客：JZ31 栈的压入、弹出序列

cpp 复制代码

bool IsPopOrder(vector<int> pushV, vector<int> popV) {
    if(pushV.size() != popV.size()) return false;
    
    int outIdx = 0, inIdx = 0;
    stack<int> s;
    
    while(outIdx < popV.size()) {
        // 当栈空或栈顶不等于待出栈元素时，继续入栈
        while(s.empty() || s.top() != popV[outIdx]) {
            if(inIdx < pushV.size())
                s.push(pushV[inIdx++]);
            else
                return false;
        }
        // 栈顶元素与出栈序列匹配，弹出
        s.pop();
        outIdx++;
    }
    return true;
}

💡 核心思路：

用栈模拟入栈和出栈过程
贪心策略：只要栈顶与目标出栈元素匹配，立即出栈
时间复杂度： O ( n ) O(n) O(n)，空间复杂度： O ( n ) O(n) O(n)

三、Queue：先进先出的可靠保障 🚶

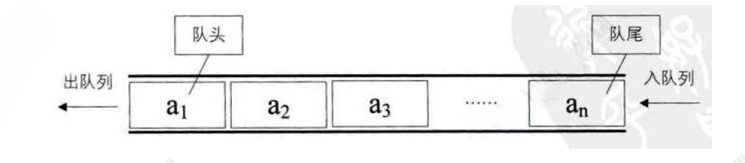
3.1 Queue接口与使用场景

queue提供FIFO操作的核心接口：

函数	说明
`queue()`	构造空队列
`empty()`	检测队列是否为空
`size()`	返回队列中有效元素个数
`front()`	返回队头元素引用
`back()`	返回队尾元素引用
`push(x)`	在队尾插入元素 x
`pop()`	删除队头元素

应用场景：

任务调度
广度优先搜索
缓冲区管理
消息队列

四、Priority Queue：堆结构的STL封装 ⛰️

4.1 Priority Queue的本质

优先级队列不是普通队列，而是堆数据结构的STL封装。默认情况下，它是大顶堆（最大元素在顶部）。

4.2 接口与自定义比较器

函数	说明
`priority_queue()`	构造空的优先级队列
`empty()`	检测队列是否为空
`top()`	返回堆顶元素
`push(x)`	插入元素 x 并调整堆
`pop()`	删除堆顶元素并调整堆

关键特性：自定义比较器

cpp 复制代码

// 创建大顶堆（默认）
priority_queue<int> maxHeap;

// 创建小顶堆
priority_queue<int, vector<int>, greater<int>> minHeap;

4.3 例题：数组中第K个最大元素

cpp 复制代码

int findKthLargest(vector<int>& nums, int k) {
    // 将所有元素放入大顶堆
    priority_queue<int> pq(nums.begin(), nums.end());
    
    // 弹出前k-1个最大元素
    for(int i = 0; i < k-1; ++i) {
        pq.pop();
    }
    
    return pq.top();
}

💡 时间复杂度分析：

建堆： O ( n ) O(n) O(n)
弹出k-1次： O ( k l o g n ) O(k log n) O(klogn)
总时间复杂度： O ( n + k l o g n ) O(n + k log n) O(n+klogn)，当k远小于n时，优于排序的 O ( n l o g n ) O(n log n) O(nlogn)

五、为什么stack和queue选择deque作为默认容器？🔍

5.1 deque：分段连续的精妙设计

deque(双端队列)：是一种双开口的"连续"空间的数据结构 ，双开口的含义是：可以在头尾两端进行插入和删除操作，且时间复杂度为 O ( 1 ) O(1) O(1)，与vector比较，头插效率高，不需要搬移元素；与list比较，空间利用率比较高。

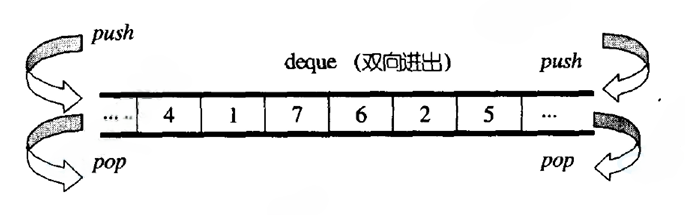
deque并不是真正连续的空间，而是由一段段连续的小空间拼接而成的，实际deque类似于一个动态的二维数组 ，其底层结构如下图所示：

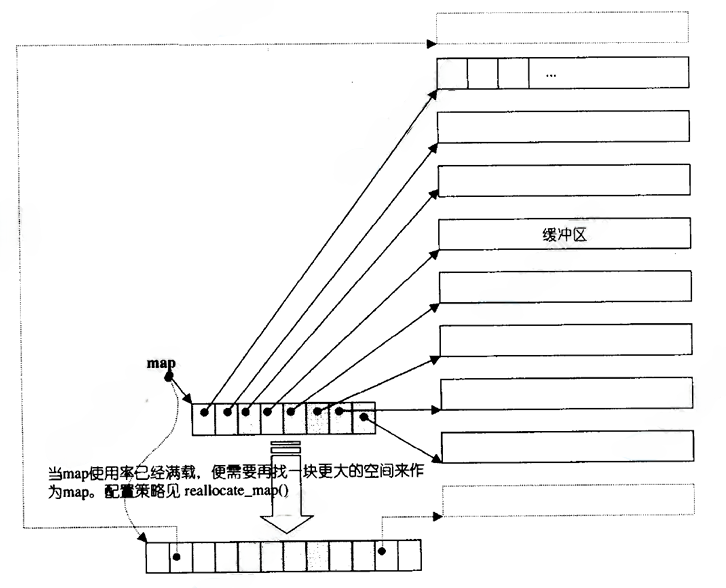
双端队列底层是一段假象的连续空间，实际是分段连续的，为了维护其"整体连续"以及随机访问的假象，落在了deque的迭代器身上，因此deque的迭代器设计就比较复杂，如下图所示：

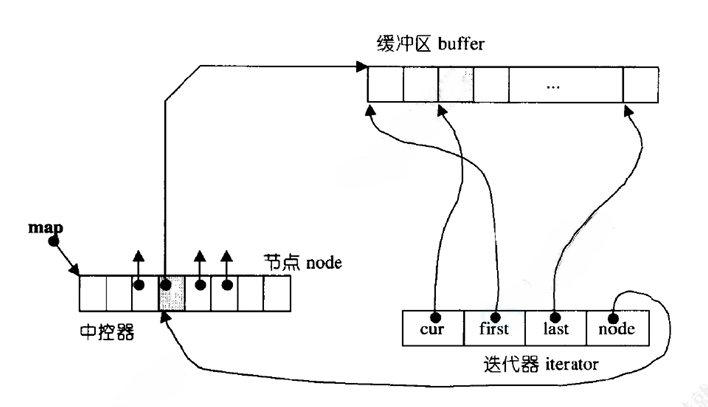
那deque是如何借助其迭代器维护其假想连续的结构呢？

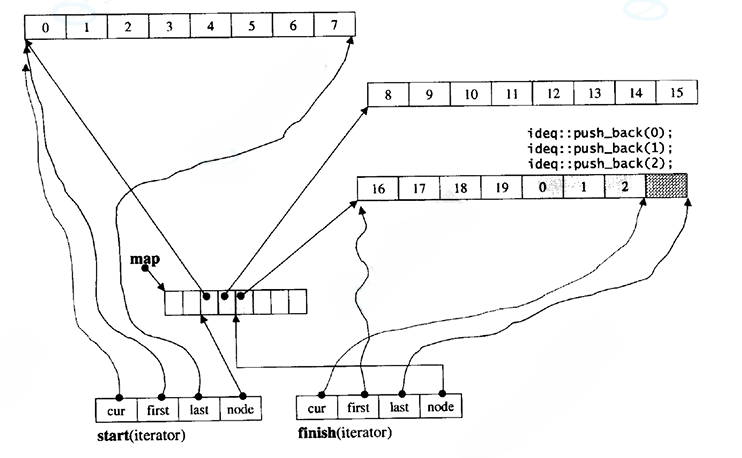
deque的头插，如上图：
1.如果缓冲区都满了的情况，则会在前面再开一个同样大小的缓冲区（8个int大小），并把头插元素放到该缓冲区的末尾位置，所以第一个有效元素 的下标不再是0，而是7；而原来下标为0的元素，下标就变为8；
2.如果第一个缓存区未满，则在第一个有效元素的前面直接放入头插元素即可。

尾插就比较简单了，就挨着最后一个元素插入，不够再创建缓冲区，头部插入即可

deque 的下标是 "全局连续" 的，不管缓冲区如何新增 / 删除，每个元素的 "全局下标" 由其插入顺序决定（头插会让后续元素下标增大，尾插则扩展下标）。

以 "头插新增缓冲区" 为例：假设原 deque 有 3 个缓冲区（每个 8 个元素），总元素 24 个，元素下标为 0~ 23。现在头插一个新缓冲区（8 个元素），则原元素的下标会变为 8~31，新元素下标为 0 ~7。

此时访问原下标 19 的元素（现在全局下标变为 19+8=27）：

计算节点：27 / 8 = 3 → 第 4 个节点（start + 3）；
计算元素位置：27 % 8 = 3 → 该节点数组的下标 3。

deque的核心优势：

头尾操作高效： O ( 1 ) O(1) O(1) 时间复杂度的头插/头删
无需内存搬移：扩容时只需分配新块，无需拷贝所有元素
空间利用率高：相比list，没有额外指针开销
随机访问支持：提供类似数组的随机访问能力

5.2 为何stack和queue选择deque？

容器	头插/头删	尾插/尾删	随机访问	内存碎片	适合场景
vector	O(n)	O(1) 摊销	O(1)	低	需要随机访问
list	O(1)	O(1)	不支持	高	频繁中间插入/删除
deque	O(1)	O(1)	O(1)	中	两端操作

选择deque的关键原因：

适配器不需要遍历：stack和queue没有迭代器，无需担心deque遍历效率低的问题
头尾操作高效：stack需要高效的尾部操作，queue需要高效的头尾操作
内存效率平衡：比list内存利用率高，比vector在头插时效率高
避免极端情况：vector在头插时O(n)的性能可能导致不可预测的延迟

📌 结论：deque完美契合stack和queue的操作特征，同时规避了自身遍历效率低的缺陷，是"合适工具用于合适任务"的经典范例。

六、模拟实现：stack、queue、priority_queue 💻

6.1 Stack的模拟实现

cpp 复制代码

namespace bit {
    template<class T, class Container = deque<T>>
    class stack {
    public:
        void push(const T& x) { _con.push_back(x); }
        void pop() { _con.pop_back(); }
        const T& top() const { return _con.back(); }
        size_t size() const { return _con.size(); }
        bool empty() const { return _con.empty(); }
        
    private:
        Container _con; // 底层容器
    };
}

💡 实现精要：

模板参数：Container允许自定义底层容器（deque/vector/list）
接口简化：仅暴露栈的核心操作，隐藏底层容器的其他功能
类型安全：通过模板保证类型一致性

6.2 Queue的模拟实现

cpp 复制代码

namespace bit {
    template<class T, class Container = deque<T>>
    class queue {
    public:
        void push(const T& x) { _con.push_back(x); }
        void pop() { _con.pop_front(); }  // 注意：deque必须支持pop_front
        const T& front() const { return _con.front(); }
        const T& back() const { return _con.back(); }
        size_t size() const { return _con.size(); }
        bool empty() const { return _con.empty(); }
        
    private:
        Container _con;
    };
}

💡 关键点：

操作对称性：push_back + pop_front实现FIFO
容器要求：底层容器必须支持队头删除操作
接口封装：将容器操作转化为队列语义

6.3 Priority Queue的模拟实现

cpp 复制代码

namespace bit {
    // 默认是大堆
    template<class T, class Container = vector<T>, class Compare = Less<T>>
    class priority_queue {
    public:
        void push(const T& x) {
            _con.push_back(x);
            AdjustUp(_con.size() - 1); // 上滤调整
        }
        
        void pop() {
            swap(_con[0], _con[_con.size() - 1]);
            _con.pop_back();
            AdjustDown(0); // 下滤调整
        }
        
        const T& top() const { return _con[0]; }
        size_t size() const { return _con.size(); }
        bool empty() const { return _con.empty(); }
        
    private:
        void AdjustUp(int child) {
            Compare com;
            int parent = (child - 1) / 2;
            while (child > 0) {
                if(com(_con[parent], _con[child])) {
                    swap(_con[child], _con[parent]);
                    child = parent;
                    parent = (child - 1) / 2;
                } else break;
            }
        }
        
        void AdjustDown(int parent) {
            size_t child = parent * 2 + 1;
            Compare com;
            while (child < _con.size()) {
                if (child + 1 < _con.size() && com(_con[child], _con[child + 1])) {
                    ++child; // 选择较大的孩子
                }
                if (com(_con[parent], _con[child])) {
                    swap(_con[child], _con[parent]);
                    parent = child;
                    child = parent * 2 + 1;
                } else break;
            }
        }
        
        Container _con;
    };
}

💡 设计亮点：

函数对象：Compare参数支持自定义比较逻辑
二叉堆实现：通过数组表示完全二叉树
高效调整：上滤(AdjustUp)和下滤(AdjustDown)保证 O ( l o g n ) O(log n) O(logn)时间复杂度
底层选择：使用vector而非deque，因为堆需要随机访问

七、性能对比：不同场景下的容器选择 📊

为了验证不同底层容器的性能差异，我们进行两个关键测试：

7.1 排序性能对比

cpp 复制代码

void test_op1() {
    srand(time(0));
    const int N = 1000000;
    
    deque<int> dq;
    vector<int> v;
    
    for (int i = 0; i < N; ++i) {
        auto e = rand() + i;
        v.push_back(e);
        dq.push_back(e);
    }
    
    int begin1 = clock();
    sort(v.begin(), v.end());
    int end1 = clock();
    
    int begin2 = clock();
    sort(dq.begin(), dq.end());
    int end2 = clock();
    
    printf("vector:%d\n", end1 - begin1);   // 通常更快
    printf("deque:%d\n", end2 - begin2);    // 通常慢1.5-2倍
}

7.2 优化策略：deque排序的最佳实践

cpp 复制代码

void test_op2() {
    // ...
    int begin2 = clock();
    // 拷贝到vector排序，再拷贝回deque
    vector<int> v(dq2.begin(), dq2.end());
    sort(v.begin(), v.end());
    dq2.assign(v.begin(), v.end());
    int end2 = clock();
    // 通常比直接对deque排序快2-3倍
}

📌 实践建议：

避免直接对deque排序：其迭代器不是原生指针，访问开销大
排序场景用vector：需要排序时，优先考虑vector
两端操作场景用deque：频繁头尾插入/删除时，deque性能优势明显
极端内存限制用list：当内存碎片不是主要问题，且需要稳定迭代器时

八、思考与总结 ✨

核心概念	关键理解
容器适配器	通过接口转换实现特定功能的数据结构封装
底层容器选择	`deque` 平衡了效率与空间需求
优先级队列	堆算法的 STL 封装，自定义比较器提供灵活性
性能权衡	没有万能容器，根据场景选择合适工具

💡 设计准则：

"适配器的精髓不在于隐藏复杂性，而在于提供恰到好处的抽象层次。"

封装适度：只暴露必要接口，隐藏实现细节
策略可替换：允许自定义底层容器和比较策略
性能可预测：操作复杂度明确，无隐藏开销
接口一致：遵循STL统一规范，无缝融入STL系统

九、下篇预告

在下一篇《C++模板进阶：从泛型到元编程的思维跃迁》中，我们将探索：

非类型模板参数的妙用与限制
函数模板与类模板的特化技巧
偏特化在STL中的经典应用
模板分离编译的陷阱与解决方案
从语言特性到设计哲学的升华

✨ 特别亮点：我们将剖析std::enable_if和SFINAE原则，揭示现代C++模板元编程的核心思想。