大家好,我们又见面了!!!之前给大家介绍了ST表,今天,这一期我将带领大家练习三道ST表相关的练习题,难度由易到难,欢迎大家前来挑战。就当作一次检验ST表学习成果的机会。
如果大家没有学过 ST 表,可以参考我的一篇关于 ST 表的博客学习一下:
创作不易,别忘了一键三连~~~
废话不多说,我们直接开始:
题目一:忠诚
1. 题目描述:
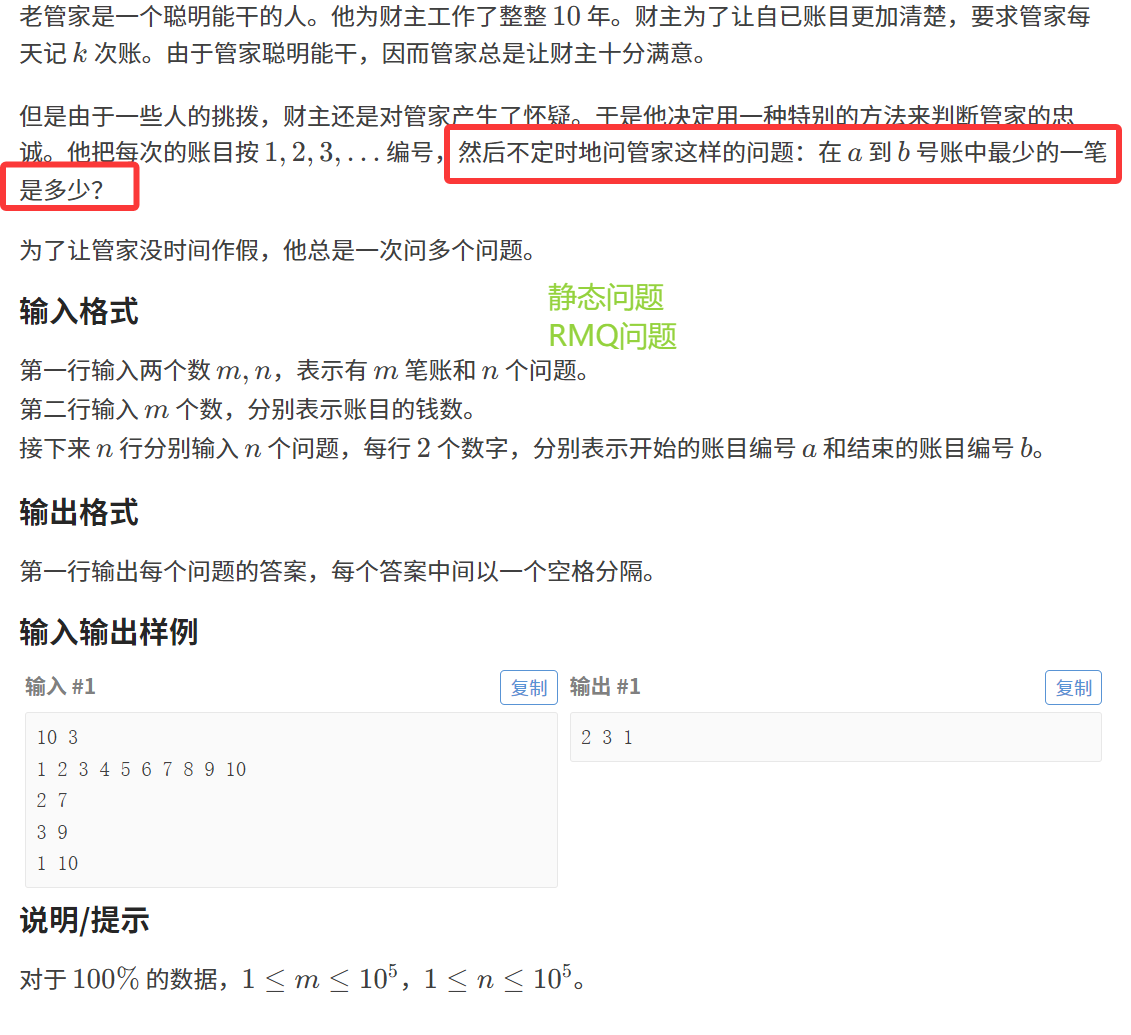
2. 算法原理:
第一道练习题,先给大家热热身。这道题就是一个简单的ST表的模板题
3. 代码实现:
cpp
#include <iostream>
#include <cmath>
#include <vector>
using namespace std;
const int N = 1e5 + 10;
int f[N][25];
int m, n;
vector<int> ret;
int query(int a, int b)
{
int t = log2(b - a + 1);
return min(f[a][t], f[b - (1 << t) + 1][t]);
}
int main()
{
cin >> m >> n;
for(int i = 1; i <= m; i++) cin >> f[i][0];
for(int j = 1; j <= log2(m); j++)
{
for(int i = 1; i + (1 << j) - 1 <= m; i++)
{
f[i][j] = min(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
}
}
while(n--)
{
int a, b; cin >> a >> b;
ret.push_back(query(a, b));
}
for(int i = 0; i < ret.size(); i++)
{
cout << ret[i] << " ";
}
cout << endl;
return 0;
}题目二:最大数
1. 题目描述:

2. 算法原理:
解法一:线段树(模板)
通过读题,发现本题是一道单点修改和区间查询相关的题目。首先应该想到的是数据结构:线段树
注意:树状数组无法求区间内的最大值,因为区间最值不满足可差分。
这道题的主流解法就是线段树,我们不要被题目的过程迷惑,直接创建一个长度为M的数组,先初始化为0,然后就是线段树单点修改和区间查询的模板了。
解法二:ST表(逆序ST表)
这道题还有一种解法,就是ST表(非主流解法),但ST表的解法不容易想到,因此,大家一定要掌握线段树的解法,如果学有余力,可以看一下下面的ST表解法。
我们之前学习ST表时,因为ST表的实现原理是预处理思想,因此ST表解决的大多都是静态问题。
但是,我们这道题比较特殊,虽然是动态问题,但是也能使用ST表解决。
这道题就不是简单的背一下ST表的模板就能解决了。要深刻理解ST表的原理!!!

由于我们是在尾部插入元素,因此并不会对之前ST表维护的信息产生影响。
对于一次尾部插入操作,我们只需要在ST表每一行最后一个元素后再插入一个元素就可以了。
那么问题来了,如何插入呢???代码如何实现呢???
如果直接去修改的话,是不太容易实现的,那我们转换一下思维,把ST表整体右移:

这样的话,只需要修改ST表的最后一列就可以了,一次循环就可以实现了。
这其实就是《逆序ST表》。
打破我们的惯性思维,仅仅修改一下状态表示和状态转移方程就能够实现。

3. 代码实现:
解法一:线段树(模板)
cpp
#include <iostream>
using namespace std;
#define lc p << 1
#define rc p << 1 | 1
typedef long long LL;
const int N = 2e5 + 10;
int n, d;
LL a[N];
struct node
{
int l, r;
LL m;
}tr[N << 2];
void pushup(int p)
{
tr[p].m = max(tr[lc].m, tr[rc].m);
}
void build(int p, int l, int r)
{
tr[p] = {l, r, a[l]};
if(l == r) return;
int mid = (l + r) >> 1;
build(lc, l, mid); build(rc, mid + 1, r);
pushup(p);
}
void modify(int p, int x, int k)
{
int l = tr[p].l, r = tr[p].r;
if(l == x && r == x)
{
tr[p].m = k;
return;
}
int mid = (l + r) >> 1;
if(x <= mid) modify(lc, x, k);
else modify(rc, x, k);
pushup(p);
}
LL query(int p, int x, int y)
{
int l = tr[p].l, r = tr[p].r;
if(x <= l && r <= y) return tr[p].m;
int mid = (l + r) >> 1;
LL ret = 0;
if(x <= mid) ret = max(ret, query(lc, x, y));
if(y > mid) ret = max(ret, query(rc, x, y));
return ret;
}
int main()
{
cin >> n >> d;
build(1, 1, n);
int cnt = 0;
LL t = 0;
for(int i = 1; i <= n; i++)
{
char op; cin >> op;
if(op == 'A')
{
cnt++;
LL x; cin >> x;
modify(1, cnt, (x + t) % d);
}
else
{
LL x; cin >> x;
t = query(1, cnt - x + 1, cnt);
cout << t << endl;
}
}
return 0;
} 解法二:ST表(逆序ST表)
cpp
#include <iostream>
#include <cmath>
using namespace std;
typedef long long LL;
const int N = 2e5 + 10;
LL m, d, n;
LL f[N][20];
int main()
{
cin >> m >> d;
LL pre = 0;
while(m--)
{
char op; LL x; cin >> op >> x;
if(op == 'Q')
{
// query [n - x + 1, n]
int k = log2(x);
pre = max(f[n][k], f[n - x + (1 << k)][k]);
cout << pre << endl;
}
else
{
LL t = (pre + x) % d;
n++;
f[n][0] = t;
for(int j = 1; j <= log2(n); j++)
f[n][j] = max(f[n][j - 1], f[n - (1 << (j - 1))][j - 1]);
}
}
return 0;
}题目三:01序列
1. 题目描述:
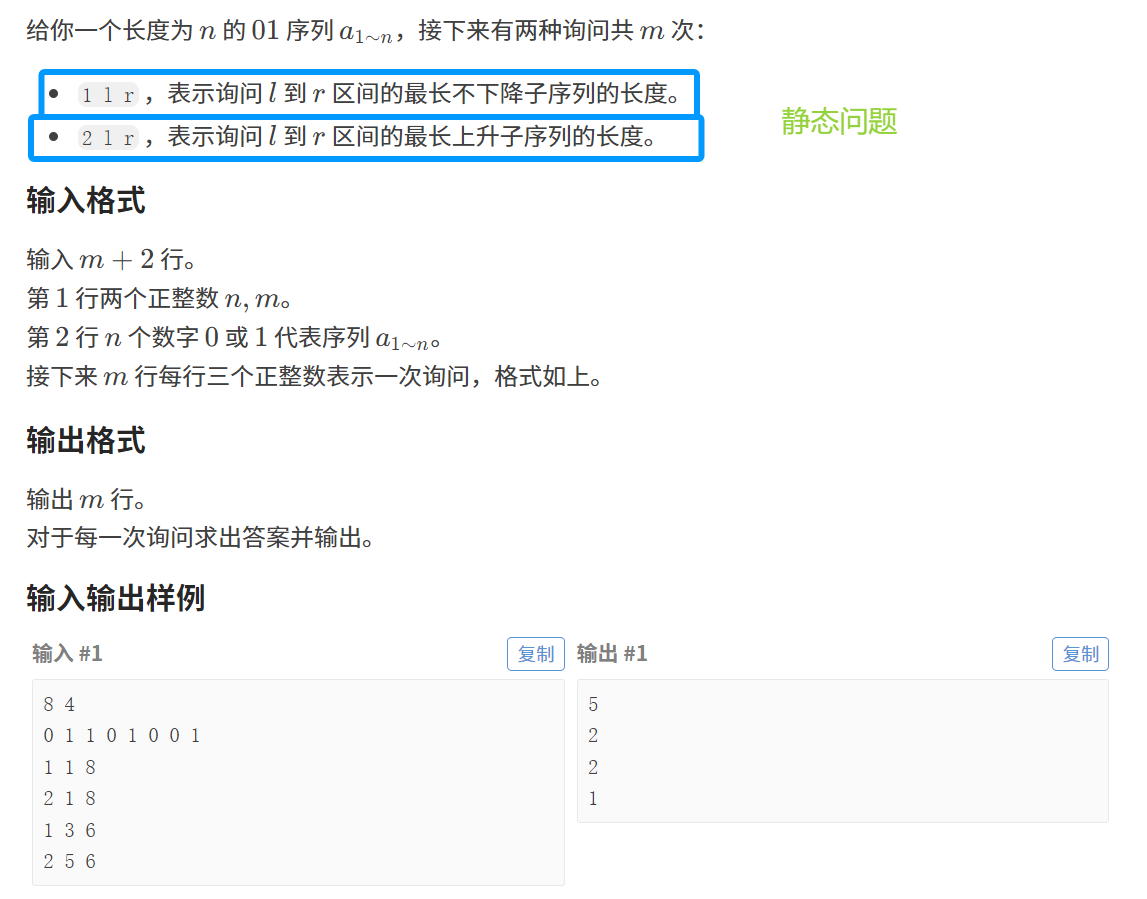
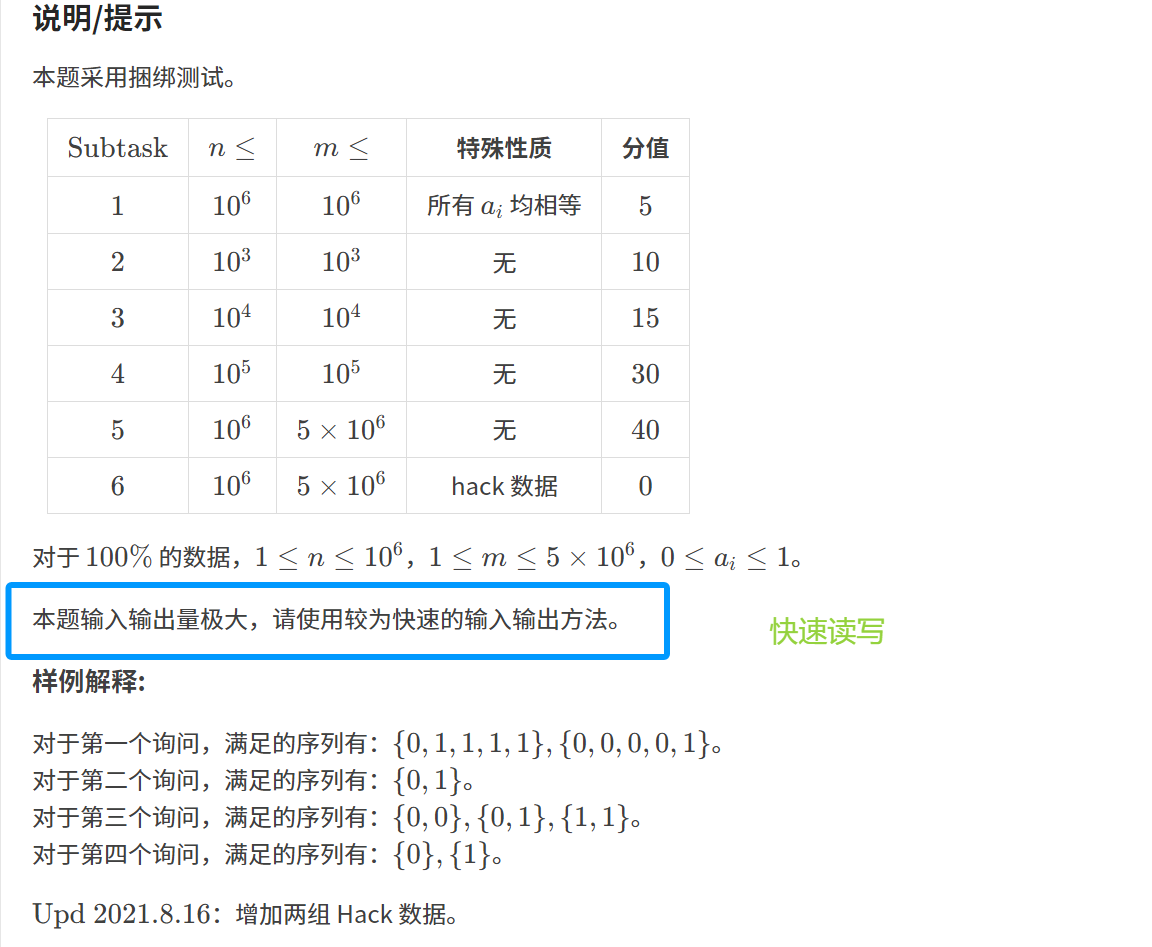

2. 算法原理:
通过读题,发现这又是一道查询相关的题目。首先想一下能不能使用一种数据结构把信息维护起来
我们发现直接维护最长不下降子序列的长度信息的是比较困难的,线段树、树状数组、ST表都不能解决。
那我们只能一步一步分析了:遇到陌生的查询问题,一定要锻炼一下自己的题目分析能力
首先考虑处理:最长不下降子序列
我们要在 [L,R] 区间内找到最长不下降子序列,我们挑出来的子序列无非就以下三种情况:
1. 挑出来的都是 0。
2. 挑出来的都是 1。
3. 挑出来的前面是 0 后面是 1。
逐一讨论就行了。
情况一: 挑出来的都是 0
我们统计 [L,R] 中一共有多少个 0 就可以了,可以使用前缀和实现。
情况二: 挑出来的都是 1
我们统计 [L,R] 中一共有多少个 1 就可以了,可以使用前缀和实现。
情况三: 挑出来的前面是 0 后面是 1
我们枚举分割点,然后结合上面的两个前缀和数组,就可以算出最长的长度。

我们对上面的那个式子进行一个化简:

我们在分析问题的过程中,发现一个子问题可以用我们学过的ST表解决!!!
这样的话,最长不下降子序列我们就讨论完了。
接下来处理第二个查询:最长上升子序列
因为题目给出的是 01 串,那么最长上升自序列的长度不是 1 就是 2(01)
存在相邻的 01 答案就是 2,否则答案就是 1。
我们可以预处理出一个数组:h[x]:表示:[1,i] 区间内,形如 "01" 这种形式出现了多少次。
然后使用前缀和的思想,如果 h[L] == h[R] 那么说明 [L,R] 内不存在 "01",答案就是 1.
如果 h[L] != h[R],说明 [L,R] 中存在 "01",答案就是 2.
如何预处理 h[x] ??? --- 动态规划:(如下图)
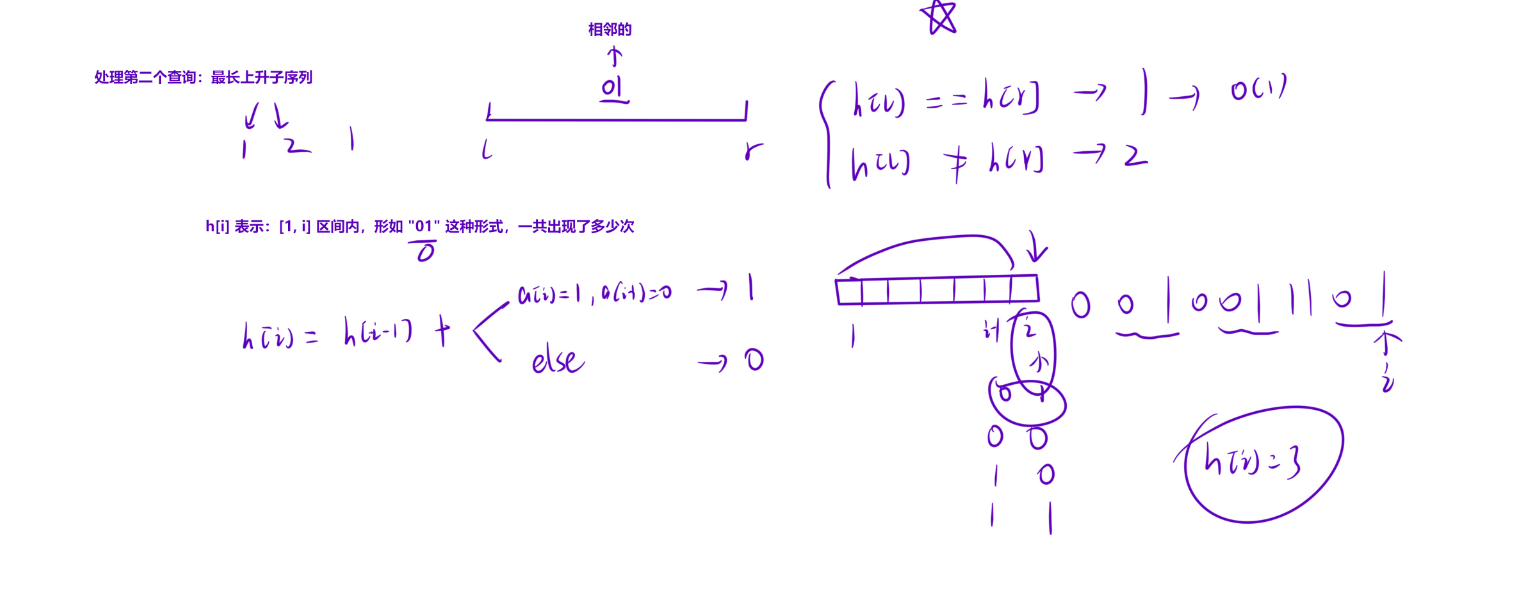
这样的话,最长上升子序列我们也讨论完了。
这道题目难度还是有的,一定要想明白。
接下来,请看代码:
3. 代码实现:
cpp
#include <iostream>
#include <cmath>
using namespace std;
const int N = 1e6 + 10;
//快速读写
int read()
{
char ch = getchar();
int ret = 0;
while(ch < '0' || ch > '9') ch = getchar();
while(ch >= '0' && ch <= '9')
{
ret = ret * 10 + ch - '0';
ch = getchar();
}
return ret;
}
void write(int x)
{
if(x > 9) write(x / 10);
putchar(x % 10 + '0');
}
int n, m;
int a[N], f[N], g[N], h[N];
int st[N][20];
int main()
{
n = read(); m = read();
for(int i = 1; i <= n; i++)
{
a[i] = read();
f[i] = f[i - 1] + (a[i] == 0);
g[i] = g[i - 1] + (a[i] == 1);
h[i] = h[i - 1] + (a[i] && !a[i - 1]);
}
//ST表 f[i] - g[i]
for(int i = 1; i <= n; i++) st[i][0] = f[i] - g[i];
for(int j = 1; j <= log2(n); j++)
{
for(int i = 1; i + (1 << j) - 1 <= n; i++)
{
st[i][j] = max(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
}
}
while(m--)
{
int op = read(), l = read(), r = read();
if(op == 1)
{
int k = log2(r - l + 1);
int ret = max(st[l][k], st[r - (1 << k) + 1][k]) + g[r] - f[l - 1];
write(max(ret, max(f[r] - f[l - 1], g[r] - g[l - 1])));
putchar('\n');
}
else
{
write(h[r] == h[l] ? 1 : 2);
putchar('\n');
}
}
return 0;
}好的,今天这一期的分享就到这里了,谢谢大家的观看,我们下一期再见!!!