这篇文章从程序员视角,类比理解 LLM 的底层原理。
阶段一:设计蓝图
LLM 现在都用 Transformer 架构,最开始也要设置一些额外的参数。
d_modle
比如 4096,是 2 的 n 次方。代表内部向量的维度,常见的 xy 轴就是二维的,左边代表比如 [1,2],4096 维度就用 [1,2,3....] 一共有 4096 个数字,所以不需要想象出 4096 维在现实世界是什么样的结构,我们用数学中的矩阵表示他们。
维度代表了思考的广度,比如我们从各个角度判断一个人,身高、体重、性别等等,每一个角度都类比一个维度。
Layers
比如 96 层,每个 4096 的矩阵代表一层,每层里面有多个 4096 的矩阵,有不同的含义。后面会详细解释。
Layers 代表思考的深度。
Vocab Size
比如 128k,这个是词汇表大小,词汇表配置了 LLM 有多少个 token。
Token 是 Tokenizer 根据统计规律切分出来的,不完全等同于中文的每个字或者因为的每个单词,还包括标点符号、词、或短语,取决于 Tokenizer 是如何切分的,比如它发现 "奥利给" 经常出现在一起,也会把这个词标记为一个 token。
这些 token 和对应的向量坐标存在 Vocab Map 和 Embedding Table 中,Map 的数据是 token 和 Id 的对应。
json
// Vocab Map
{
"apple": 501,
"cat": 882,
"Java": 998,
"love": 1024
}Embedding Table 中存的是 Id 和向量坐标,形状是[ VocabSize, d_modle],即 [128k,4096]。
这里要重点解释下形状和向量。
Shape 形状和 Vector 向量
形状的 [128k,4096] 表示 128k 行,4096 列的矩阵。
向量的 [128k,4096] 表示一个点在二维坐标系的方向和大小,先找到这个点的坐标,再从原点当起点画条线连接上这个点,就是向量。这个向量的形状是 [1,2],因为是 1 行 2 列。
后续我都会严格的区分形状和向量,可以停顿下理解两者的区别。

阶段二:预训练
在阶段一中设置好所有参数,阶段二就是通过海量数据学习,配置这些参数(矩阵)。
我们说的 LLM 好不好用,就是取决于这些 token 在向量的坐标地址、矩阵的转换等等是否合理。
举个例子,比如在阶段 1 定义了 2 个参数(实际上 LLM 要多得多,光 GPT3 就有 1760 亿),类比代码中新建一个对象 new Person() 有身高和体重两个参数。
经过阶段二后,这个对象就被默认赋值身高 170,体重 70kg(默认向量地址)。
而当上下文出现男字后,这个属性就变成了 175 和 75kg,出现女字就变成 165 和 55kg(矩阵转换)。
向量的位置
还记得阶段一说的 Embedding Table 是一个形状为 [128k,4096] 的矩阵吗?通过 Transformer 训练后,LLM 决定把 "人" 这个 Token 放到一个特定的坐标 [1.3,0,4...]一共 4096 位。
我们不知道为什么是这个坐标,这是 LLM 黑盒的地方,既不知道 Why 但知道 How(Transformer 训练)。
"人" 这个字在中文里有太多含义,男人、女人、好人、好人等等,这些词又是不同的向量,向量正是这些向量合并的均值。

矩阵转换
如果上下文有 "男" 这个字,整句话(其实是最后一句话最后一个 token 的向量,后面再解释)的向量就会朝着 "男人" 这个 token 的位置偏一点。
转换的方式,就是用的矩阵乘法。
举个例子解释这种转换,假设公司有 5 个初级 3 个中级 1 个高级开发工程师,用一个形状为 [3,1] 的矩阵表示,矩阵内容是 <math xmlns="http://www.w3.org/1998/Math/MathML"> v i n = [ 5 3 1 ] v_{in} = \begin{bmatrix} 5 \\ 3 \\ 1 \end{bmatrix} </math>vin= 531 。
如果想知道他们的总薪资成本和总代码量,这是个形状为 [2,1] 的矩阵,如何转换?
这就需要一个形状为 [2,3] 的规则矩阵,这里面定义了不同级别工程师的薪资和代码量。 <math xmlns="http://www.w3.org/1998/Math/MathML"> M = [ 10 20 50 200 500 1000 ] M = \begin{bmatrix} 10 & 20 & 50 \\ 200 & 500 & 1000 \end{bmatrix} </math>M=[1020020500501000]
M 规则矩阵表示初级的薪资 是 10 代码量是 200,中级是 20 和 500,高级是 50 和 1000。
然后使用矩阵乘法。
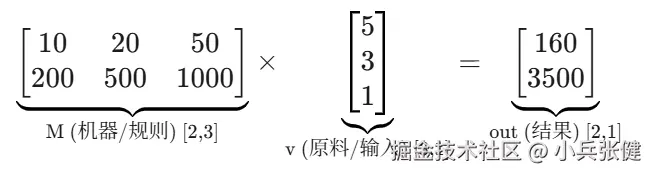
矩阵乘法就是用前一个矩阵横行每一个值,乘以第二个矩阵纵列每一个值,即 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( 10 × 5 ) + ( 20 × 3 ) + ( 50 × 1 ) = 160 (10 \times 5) + (20 \times 3) + (50 \times 1)= 160 </math>(10×5)+(20×3)+(50×1)=160, <math xmlns="http://www.w3.org/1998/Math/MathML"> ( 200 × 5 ) + ( 500 × 3 ) + ( 1000 × 1 ) = 3500 (200 \times 5) + (500 \times 3) + (1000 \times 1) = 3500 </math>(200×5)+(500×3)+(1000×1)=3500,这就是点积。
简短解释下点积,点积是计算两个向量相似度的。
<math xmlns="http://www.w3.org/1998/Math/MathML"> A = [ a 1 , a 2 , a 3 ] A = [a_1, a_2, a_3] </math>A=[a1,a2,a3]
<math xmlns="http://www.w3.org/1998/Math/MathML"> B = [ b 1 , b 2 , b 3 ] B = [b_1, b_2, b_3] </math>B=[b1,b2,b3]
<math xmlns="http://www.w3.org/1998/Math/MathML"> A ⋅ B = ( a 1 × b 1 ) + ( a 2 × b 2 ) + ( a 3 × b 3 ) A \cdot B = (a_1 \times b_1) + (a_2 \times b_2) + (a_3 \times b_3) </math>A⋅B=(a1×b1)+(a2×b2)+(a3×b3)
值为正数说明相似度很大,为 0 说明垂直(正交)没有关系,为负数说明方向相反。
回到矩阵乘法,这里要注意,规则矩阵 M 是放在前面的,不能反过来,矩阵乘法中第一个矩阵的列数必须等于第二个矩阵的列数,上面的计算用形状表示就是 [2,3] * [3,1] = [2,1]。
现在应该对矩阵乘法有个大致认知了吧,规则矩阵 * 原始值矩阵 = 结果矩阵,就是这么回事,不用太在意是怎么乘到底怎么算,只需要记住他们可以通过矩阵乘法转换。
LLM 中大量用到的这种转化,这也是我们刚刚说 "人" 的向量会偏向 "男人" 的原因,但实际上更复杂和精妙,让我们正式进入 Transfer 架构。