一、HashMap
1.1 成员变量与构造方法
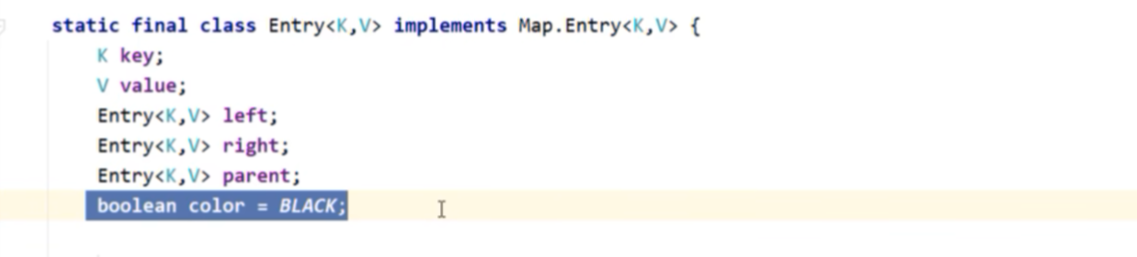
每一个Entry对象内部的属性有:key(键)、value(值)、left(左子节点地址值)、right(右子节点地址值)、color(该节点的颜色)。
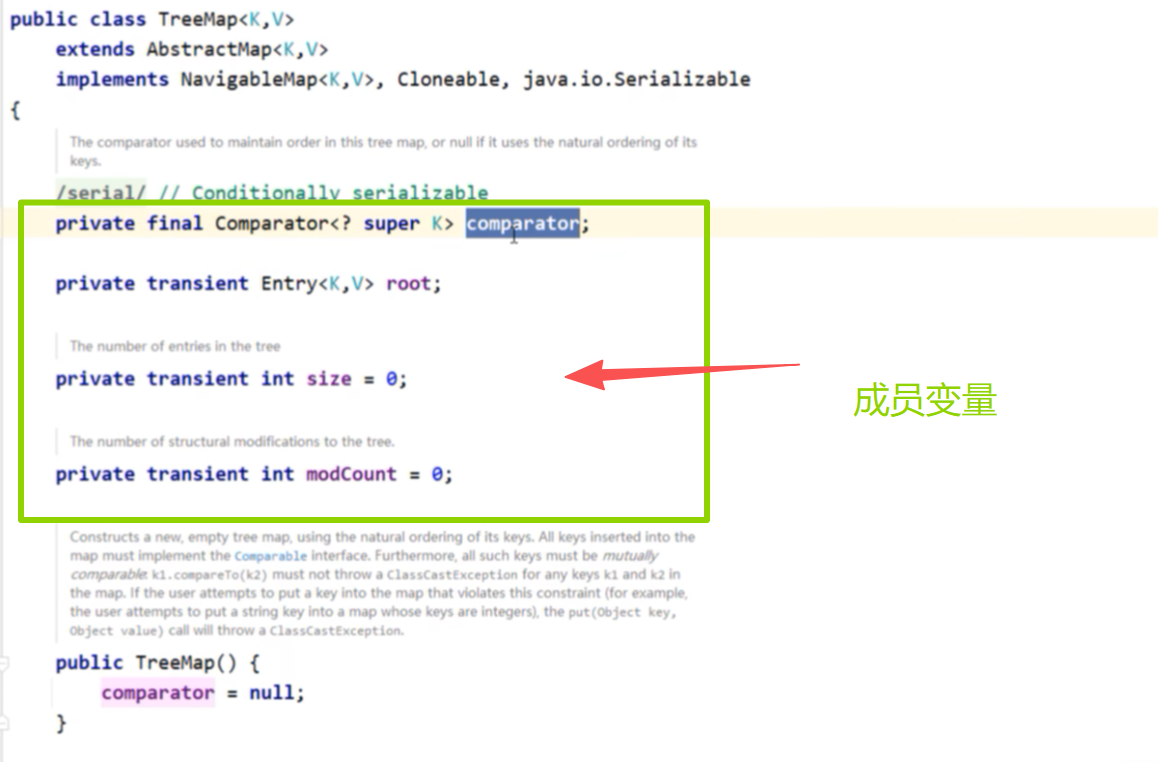
TreeMap中的成员变量目前需要了解的三个:
comparator比较的规则;
root 记录根节点的地址值;
size 表示集合的长度,也表示红黑节点的个数;
空参构造中没有传递任何的数据。
comparator = null ; 表示没有任何比较器对象。
带参构造:我们需要把比较器对象传递给其参数,然后赋值给我们的成员变量。

1.2 添加元素分析
1.2.1 首次添加元素
在添加的时候,传递两个参数(K key,V value); 其方法内部又调用了三个参数

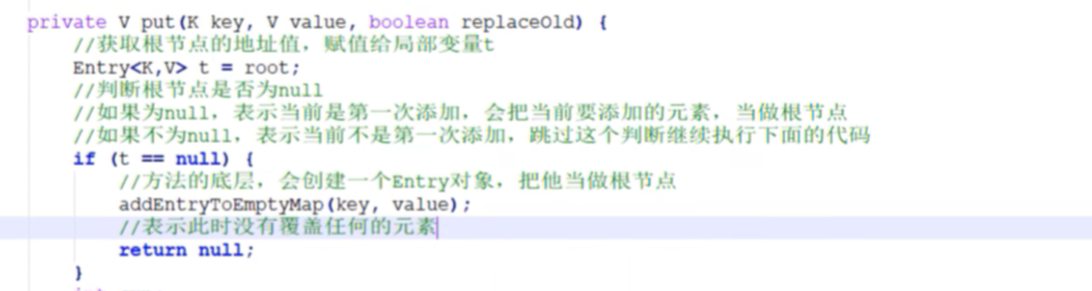
① 查看重写put的方法体,root在此之前已经说过是全局变量(成员变量),表示根节点的地址值。这里是模拟首次添加元素,所以此时局部变量t记录的是null。
② 对t的是否空的if判断语句,其中addEntryToEmptyMap(key,value)方法是将其首次添加的元素设置为根节点。return null 之后下面的代码就不走了。
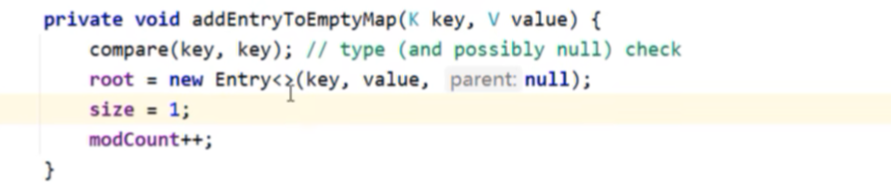
addEntryToEmptyMap(key,value)其底层源码:
compare(key, key) :调用 compare 方法,传入相同的 key 作为参数。这通常用于类型检查(确保 key 的类型正确)和可能的空值检查。
核心逻辑:
创建了一个Entry的对象(Entry是TreeMap的一个内部类,创建类的对象),并且把这个地址值赋值给了root根节点(parent null)。同时将size长度设置为1,表示已经添加成功集合中已经有一个元素存在。
modCount 通常用于记录映射的修改次数,以便在迭代过程中检测是否发生了结构上的修改。
1.2.2 两次添加元素
第二次添加元素,此时root根节点已经有了元素,if判断语句不成立,直接执行下面的代码。
① cpm:表示两个键比较之后的结果。它是通过 comparator(比较器)的 compare 方法来比较 key 和 t.key 之后得到的整数值。
- 如果
cmp < 0,表示key小于t.key,代码会进入左子树(t = t.left;)。 - 如果
cmp > 0,表示key大于t.key,代码会进入右子树(t = t.right;)。 - 如果
cmp == 0,表示key等于t.key,此时会进行值的替换或返回旧值。
② Entrt<K,V> parent ; 当我们添加第二个元素,是成为根节点的左子节点还是右子节点呢?现在目前不知道啊,但是唯一能确定的就是其父节点一定就是根节点!这里parent获取的就是根节点root的地址值。


③ cpr:记录比较规则 (Comparator 是 Java 中的一个接口,用于定义对象之间的比较规则。在对集合(如 List)进行排序时,可以使用 Comparator 来定义自定义的排序规则。)

④ if语句判断是否有比较器对象。
这里看空参,即没有传递比较器的情况,其实两者代码大致相同,搞明白即可。

⑤ 把"键"进行强转,强转成comparable类型的 (Comparable 类型是 Java 中的一个接口,它允许对象进行自然排序。具体来说,一个类如果实现了 Comparable 接口,就必须提供一个 compareTo 方法,该方法定义了对象之间的比较规则。)
do - while循环不断的去找,判断条件为t != null 表示根节点的右子节点指向的是null停止循环,
注意:这里t 就像是一个比较器的手电筒(指引针),如果插入的元素比根节点大,去右边找,就能找到这个节点!
t 是记录我们root根节点的临时变量 赋值 给我们parent,意思是把root根节点当作当前节点的父节点。
调用compareTo方法调用根节点t.key的键值跟 当前k添加的节点的 键 按照cmp 比较器的方式进行比较。
如果为负数,去左子节点找;
如果为正数,去右子节点找;
如果为0,覆盖旧有的"值"数据,具体:
- 获取旧值
oldValue = t.value - 如果
replaceOld为true或oldValue为null,则用新值替换旧值 - 返回旧值
return oldValue;(表示覆盖了旧值)
addEntey()是具体的添加元素节点的方法。
1.3 第三次添加元素
假设第三次添加的元素大于上两次添加的元素,一样重复上述规则,此时形成的红黑树是违背红黑树规则的,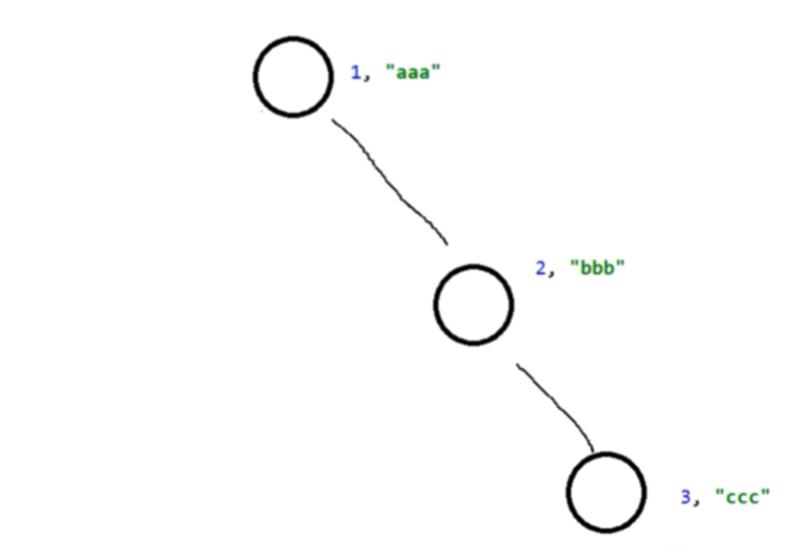
在addEntey()中具体还做了相应的调正:
首先还是创建了Entry()对象
如果你添加是父节点的左子节点,那么就把父节点的左子节点的left,记录为当前的节点e;
如果你添加是父节点的右子节点,那么就把父节点的右子节点的right,记录为当前的节点e。
互相记录,互相认亲,一个认亲老爸、一个认亲儿子。
fixAfterInsertion(e): 就是按照红黑树的规则进行调整。
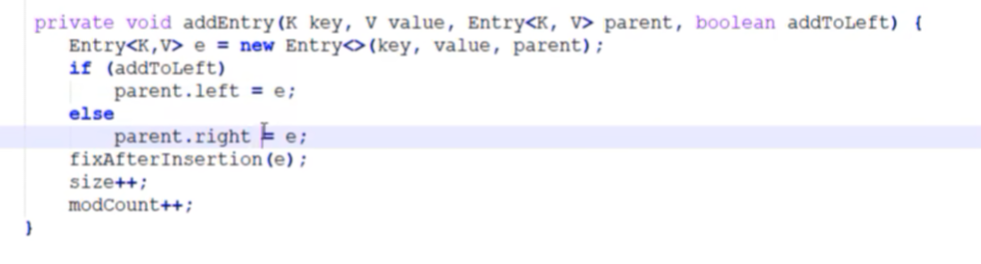
fixAfterInsertion(e):
第一步就是调整颜色

后续代码:



循环条件
1while (x != null && x != root && x.parent.color == RED) {- 条件 :当
x不为null且x不是根节点且x的父节点为红色时,进入循环。 - 目的:确保红黑树的性质(红色节点不能有红色的子节点)。
父节点是祖父节点的左子节点
1if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {- 条件 :
x的父节点是其祖父节点的左子节点。 - 目的 :确定
x在树中的具体位置,以便进行相应的调整。
叔叔节点为红色
1Entry<K,V> y = rightOf(parentOf(parentOf(x)));
2if (colorOf(y) == RED) {
3 setColor(parentOf(x), BLACK);
4 setColor(y, BLACK);
5 setColor(parentOf(parentOf(x)), RED);
6 x = parentOf(parentOf(x));
7}- 条件 :
x的叔叔节点(祖父节点的右子节点)为红色。 - 操作 :
- 将
x的父节点和叔叔节点设为黑色。 - 将祖父节点设为红色。
x指向祖父节点,继续检查更高层的节点。
- 将
叔叔节点为黑色且 x 是右子节点
1else {
2 if (x == rightOf(parentOf(x))) {
3 x = parentOf(x);
4 rotateLeft(x);
5 }
6 setColor(parentOf(x), BLACK);
7 setColor(parentOf(parentOf(x)), RED);
8 rotateRight(parentOf(parentOf(x)));
9}- 条件 :
x的叔叔节点为黑色且x是其父节点的右子节点。 - 操作 :
x指向其父节点。- 对
x进行左旋转。 - 将
x的父节点设为黑色,祖父节点设为红色。 - 对祖父节点进行右旋转。
父节点是祖父节点的右子节点
(代码结构与上述类似,但方向相反)
最终操作
1root.color = BLACK;- 操作:将根节点设为黑色,确保红黑树的性质。
声明:
分析借鉴于通义AI
以上均来源于B站@ITheima的教学内容!!!
本人跟着视频内容学习,整理知识引用