lcr90
return max(dp(nums,1),dp(nums,2)+nums[0])
如何 实现 对环的处理的呢?
通过 对第一个位置的 选 不选
将dp 隔离为一个函数,两次调用~
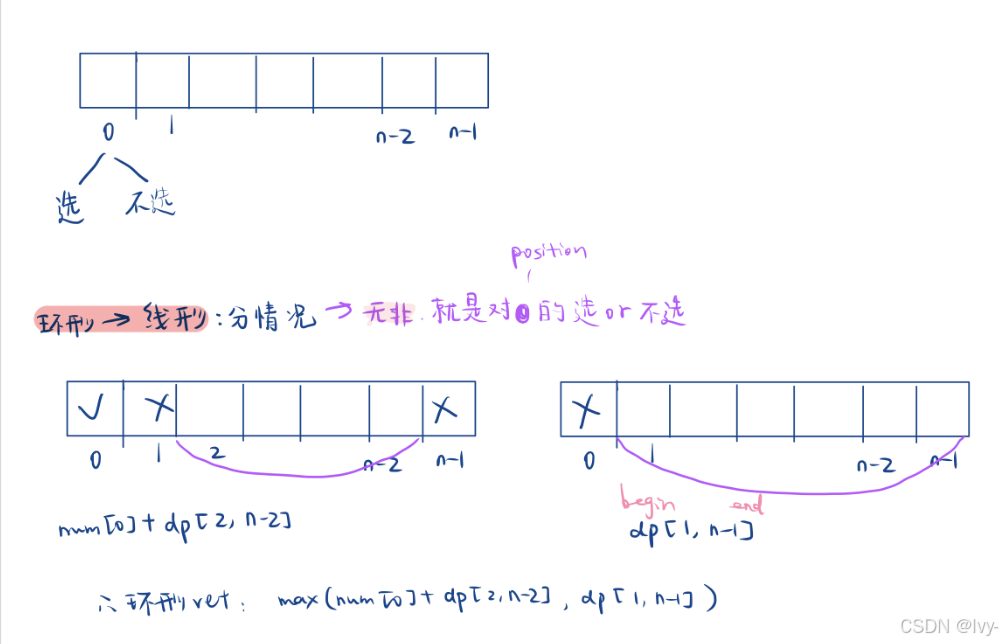
class Solution {
vector<int> nums;
public:
int rob(vector<int>& nums)
{
if(nums.empty())
return 0;
this->nums=nums;
int n=nums.size();
++return max(nums[0]+solve(2,n-2),solve(1,n-1));++//nums[0]选 不选的预讨论
}
int solve(int a,int b)
{
if(a>b) return 0;
vector<int> t(nums.begin()+a,nums.begin()+b+1);//ok
int n=t.size();
vector<vector<int>> dp(n+1,vector<int>(2,0));//0选
for(int i=1;i<=n;i++)
{
dp[i][0]=dp[i-1][1]+t[i-1];
dp[i][1]=max(dp[i-1][1],dp[i-1][0]);
}
++return max(dp[n][0],dp[n][1]);++
}
};
lc2708
维护"到第i位的最大乘积"和"到第i位的最小乘积"两个状态
考虑当前数与前序最大/最小乘积的乘法组合
推导出整个数组的最大小组实力值(乘积)
class Solution {
public:
long long maxStrength(vector<int>& nums) {
int const N = nums.size();
// dp[0][i]: maximum strength from 0 - i pos.
// dp[1][i]: minimum strength from 0 - i pos.
vector<vector<long long>> dp(2, vector<long long>(N, 0));
dp[0][0] = nums.front();
dp[1][0] = nums.front();
for (int i = 1; i < N; ++i) {
long long const num = nums[i];
dp[0][i] = max(max(dp[0][i - 1], num),
max(dp[0][i - 1] * num, dp[1][i - 1] * num));
dp[1][i] = min(min(dp[1][i - 1], num),
min(dp[0][i - 1] * num, dp[1][i - 1] * num));
}
return dp[0][N - 1];
}
};
lc2304
bfs和floyd tle麻了,想到dp了🤡🖐🏻
定义DP状态: dp[i][j] 表示从网格第一行走到第 i 行第 j 列的最小路径成本
确定初始状态:第一行无需移动, dp[0][j] 直接等于网格第一行对应位置的值 grid[0][j]
推导状态转移方程:第 i 行第 j 列的最小成本,等于上一行所有列 k 到当前列的成本(上一行成本+移动成本+当前格值)的最小值,即 ++dp[i][j] = min(dp[i-1][k] + moveCost[grid[i-1][k]][j] + grid[i][j])++
明确遍历顺序:从上到下、从左到右
确定最终结果:最后一行所有列的最小路径成本中,最小值即为整个网格的最小路径成本
(初看题目movecost确实有点长,但代码写起来还是挺丝滑的说
class Solution {
public:
int minPathCost(vector<vector<int>>& grid, vector<vector<int>>& moveCost) {
auto dp = grid;
int m = grid.size(),n = grid.back().size();
for(int i = 1; i < m; ++i){
for(int j = 0; j < n; ++j){
int base = grid[i][j];
dp[i][j] = INT_MAX;
for(int k = 0; k < n; ++k){
++dp[i][j] = min(dp[i][j],
dp[i - 1][k] + moveCost[grid[i - 1][k]][j] + base);++
}
}
}
return *(min_element(dp.back().begin(),dp.back().end()));
}
};