前言
🎯 学习目标
-
建立深度学习所需的基础数学直觉
-
知道什么是"模型、参数、损失函数、梯度下降"
-
入门机器学习的最基本流程
📌 本周必须搞懂
-
线性代数:向量、矩阵、矩阵乘法
-
微积分:偏导、链式法则
-
概率:高斯分布、期望、方差
-
机器学习流程:训练 → 验证 → 测试
-
什么是"过拟合、欠拟合"
🎬 推荐学习资源
-
线性代数可视化(强推)
B站:搜索 "3Blue1Brown 线性代数"
🧠 学完后你应该能回答
-
为什么深度学习需要矩阵乘法?
-
什么是梯度?为什么梯度下降能优化模型?
-
标准差和方差是什么?
-
什么是训练集 / 验证集 / 测试集?
🧪 实践任务
-
写一个简单的线性回归(不用 PyTorch,用 Python 实现)
-
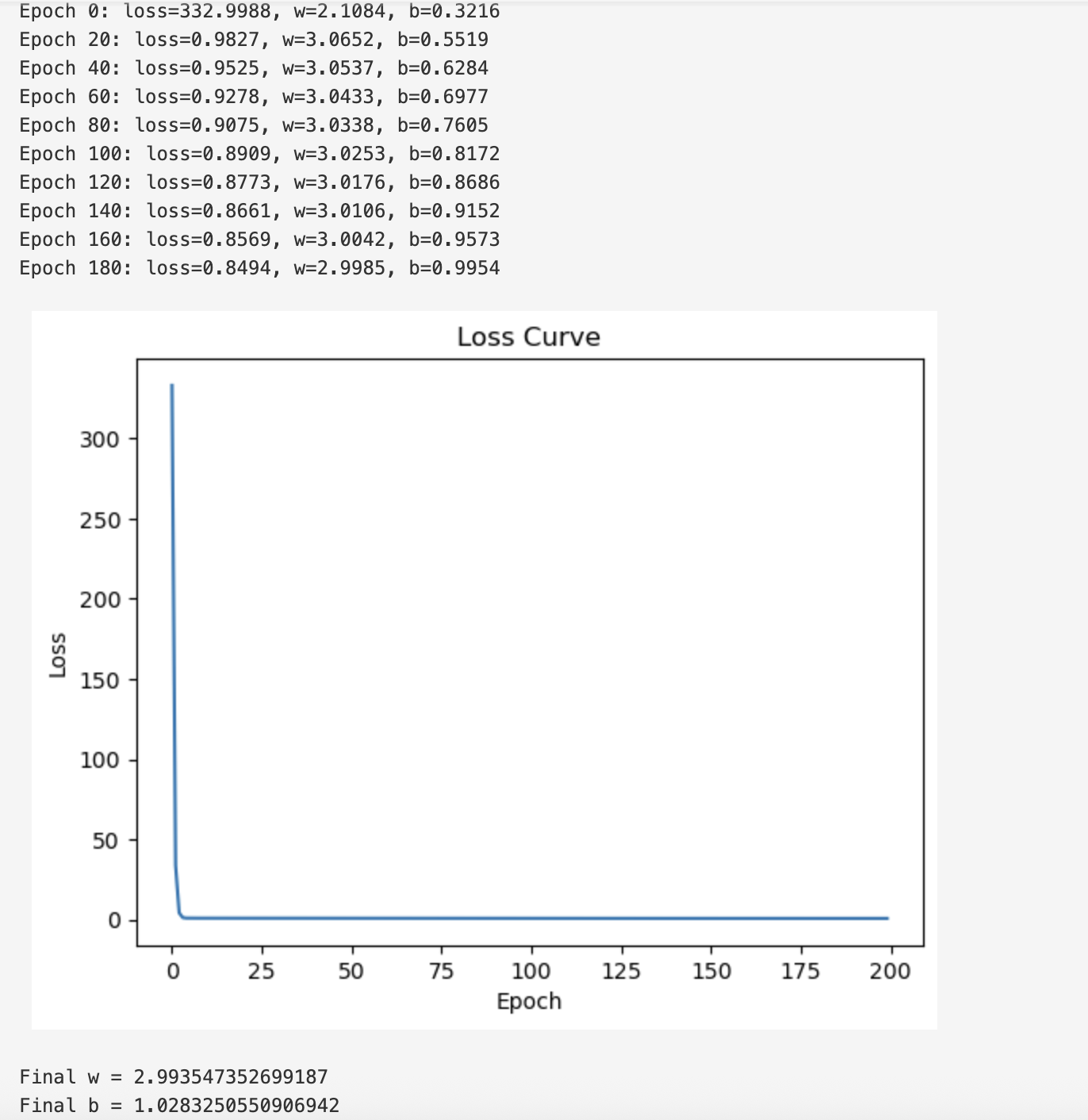
用梯度下降拟合 y = 3x + 1
-
手写损失函数、手写梯度
-
-
画出损失下降曲线(matplotlib)
1. 线性代数
线性组合,张成的空间与基
张成的空间?
1.1 基
其他任何向量都可以表示为基向量的线性组合。
线性无关、线性相关?
1.2 矩阵乘法
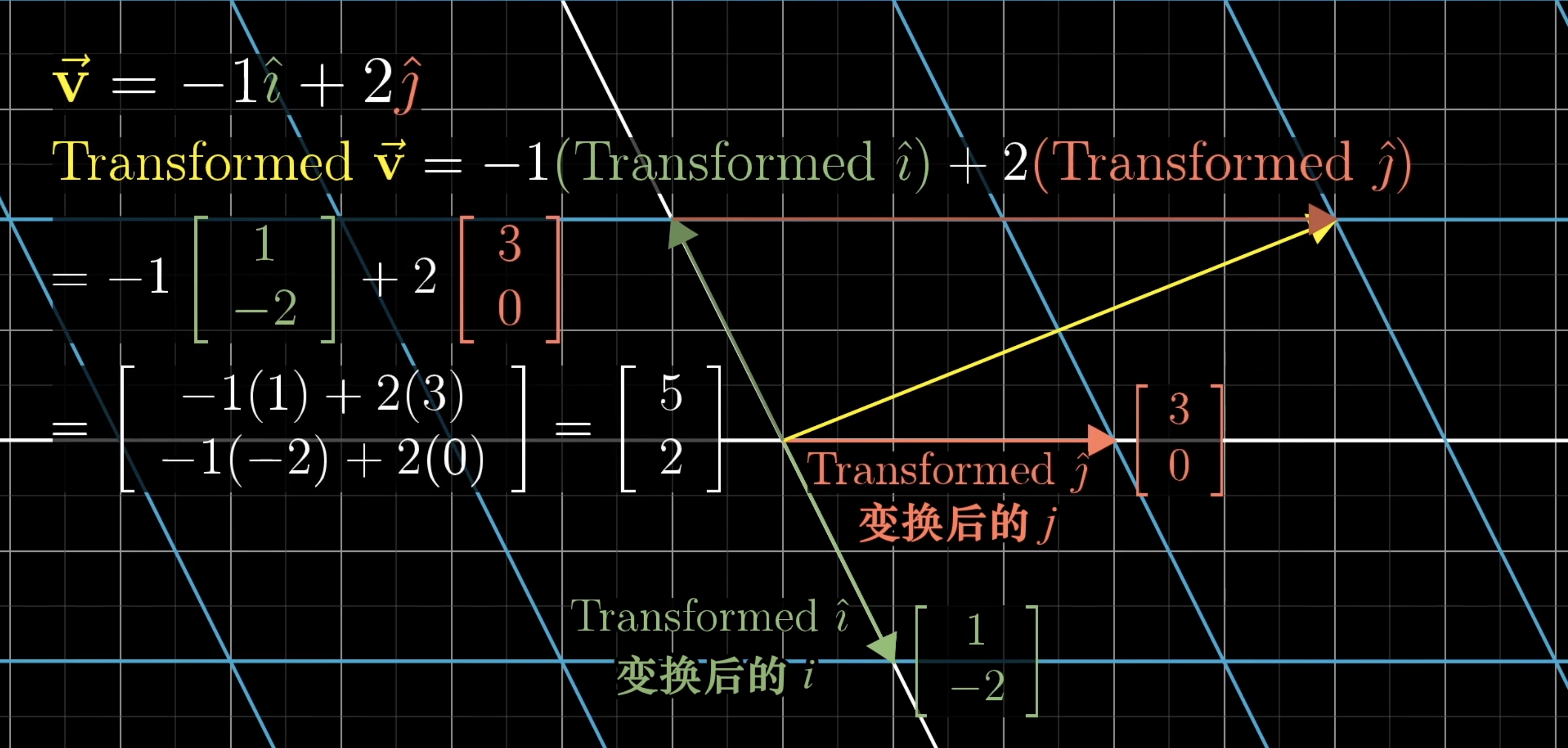
一个二维线性变换仅由4个数字完全确定,变换后的两个坐标和变换后
的两个坐标。
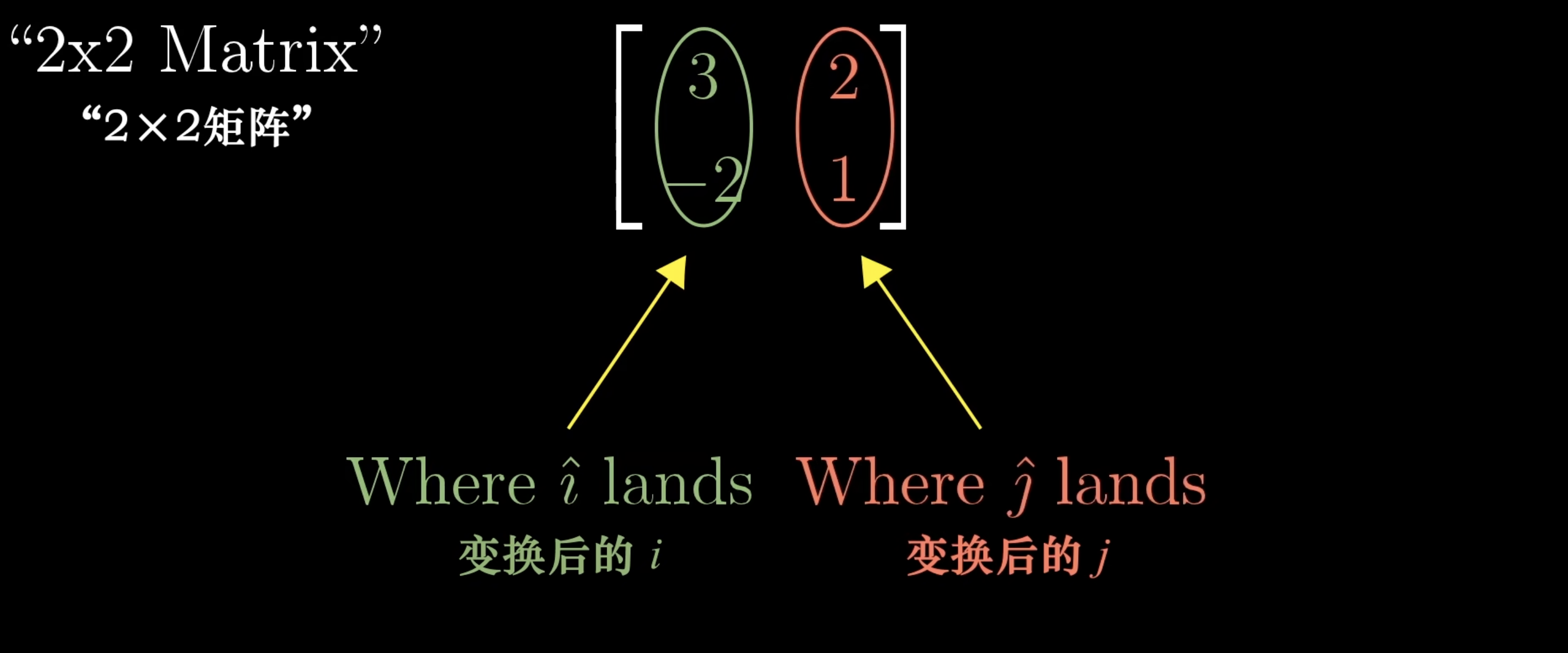
把坐标包裹在2✖️2的格子中,即矩阵。
矩阵向量乘法就是计算线性变换作用于给定向量的一种途径(一个矩阵✖️一个向量,就是将线性变换作用于该向量)
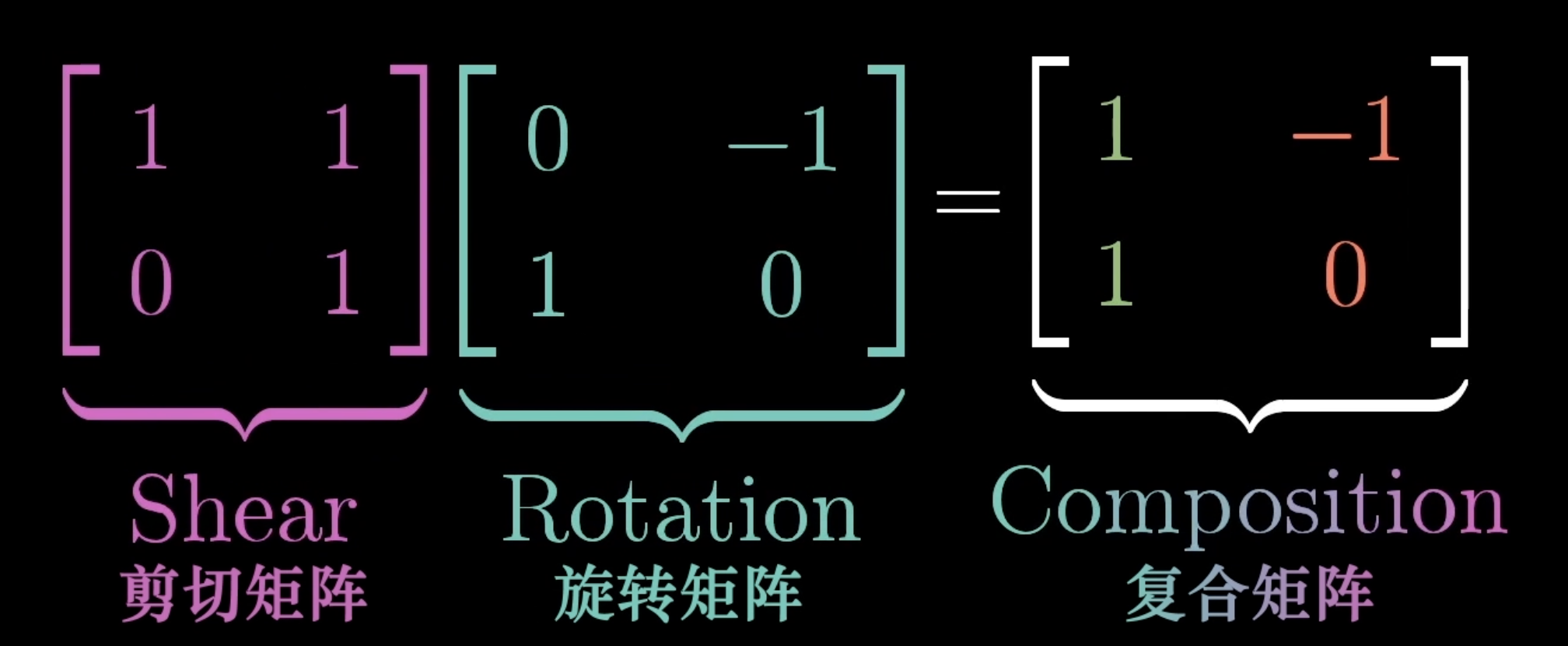
矩阵乘法。交换律❌ 结合律✅
✅结合律-- (AB)C=A(BC) 变换的顺序不同,但是变换之后的结果还是一样的
❌交换律-- ABBA (第一个矩阵输出的基向量方向不同,第二个矩阵作用在不同方向上,结果就不同)(保留)
三维空间的线性变换也类似。
📍矩阵乘法本质上是:
把输入向量 x 投影到新的特征空间。
神经网络就是不断改变数据的空间表示 → 提取特征。
1.3 行列式
矩阵所带来的线性变换使得一个给定区域面积增大或者减小的比例。(三维就是体积)
二维行列式=0,说明将平面压缩到一条线上,甚至是一个点上。(三维空间也是,三维行列式=0,说明将空间压缩至一个平面或者一条线,甚至是一个点上)
--也就是说知道一个矩阵的行列式是否为0,可以知道这个矩阵代表的变换是否将空间压缩到更下的维度上。
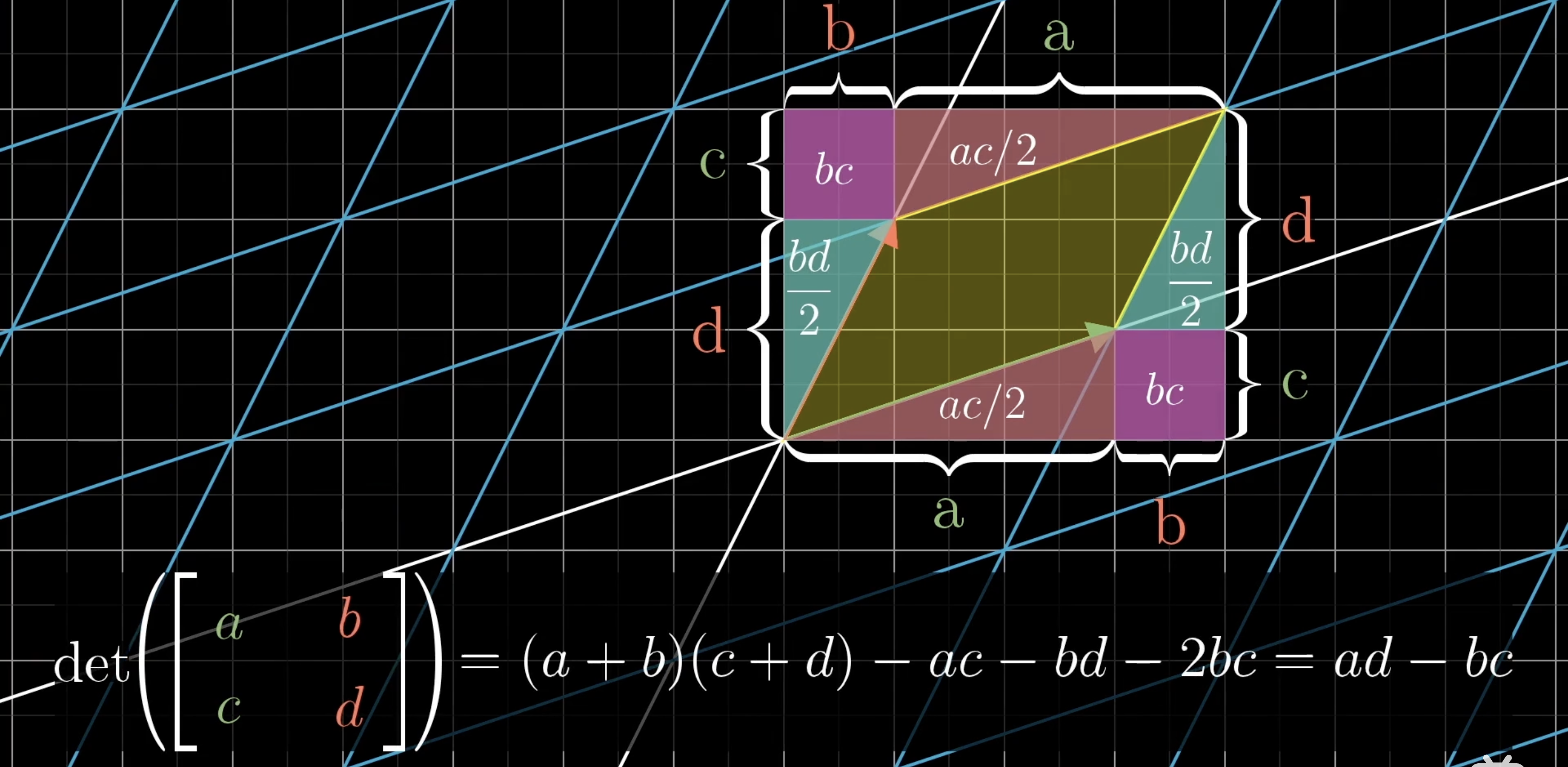
行列式有正有负,那么行列式为负代表什么呢?
初始状态在
的左侧

变换后在
的右侧,说明空间的定向发生了改变

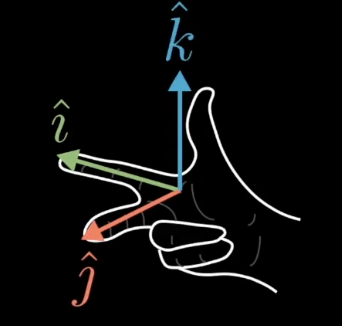
如果变换后,还是可以这么做,说明定向没有改变,行列式为正。
1.4 线性方程
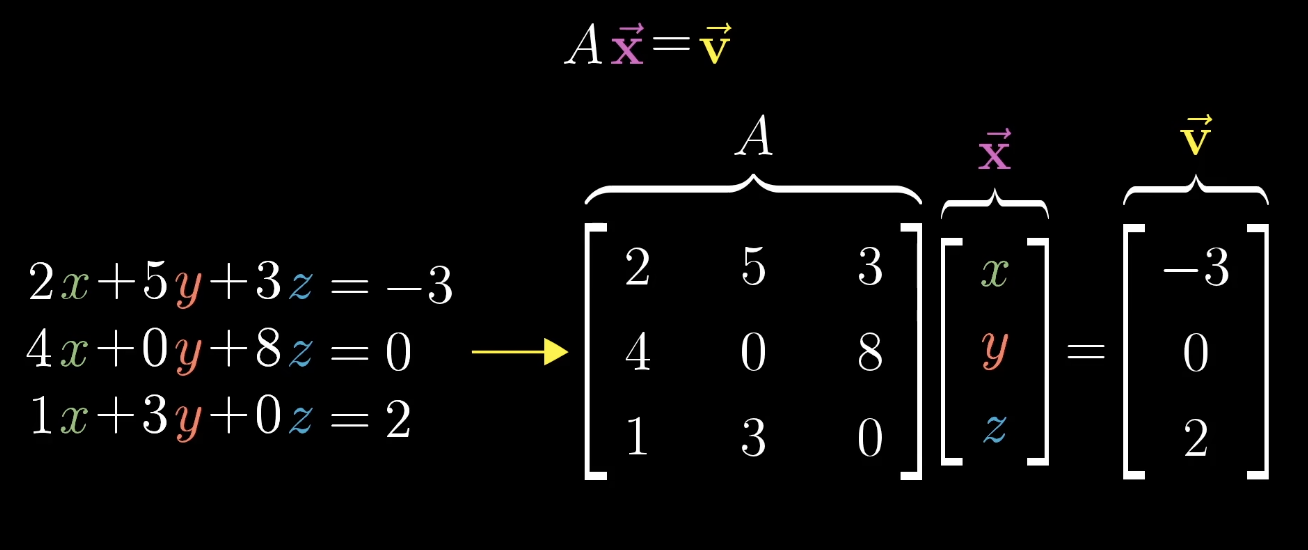
求救方程意味着去寻找一个向量,使得它在变换后和
重叠。
行列式不等于0 (对于二维来说,就说明没有压缩成一条直线或者一个点),说明只有一个向量和v重叠,并且可以逆向进行变换找到这个向量。
(det(A)0,A可逆)
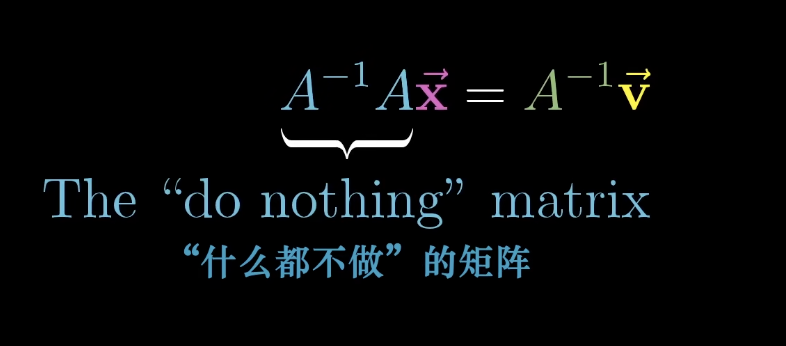
行列式=0,没有逆变换(二维,没有办法将一条线解压为一个平面),也可能有解
刚好落到压缩的直线上(det(A)==det(A,
)),就有解,否则没有解。

当v为零向量时,零空间就是这个向量方程所有可能的解。
1.5 逆矩阵
=一个什么都不做的矩阵,保持
和
不变。
1.6 秩
变换后空间的维数
当秩与列数相等,秩达到最大值,称为满秩。
1.7 零空间
对于变换后的一些向量落在零向量上,零空间就是这些向量所构成的空间。
2. 微积分
2.1 偏导数
偏导数是在多变量函数中,只改变一个变量时,函数的变化率。
2.2 链式求导

深度学习的网络层层嵌套,需要用链式法则从输出把梯度传回输入。
3. 概率论
3.1 高斯分布(正态分布)

3.2 期望

4. 反向传播

5. 数据集
训练集:训练模型,更新参数。
验证集:在训练过程中用于调参数(超参数)、早停、选择最优模型。
测试集:评估模型在没有见过的数据集上的性能。
6. 过拟合和欠拟合
6.1 过拟合
在训练集上效果好,在测试集上效果不好。说明模型在"记住训练集",而不是"学会泛化"。
6.1.1 原因
-
模型太复杂
-
数据太少
-
参数太多
-
训练太久
-
特征噪声大
6.1.2 解决方法
-
数据增强(最有效)
翻转、旋转、裁剪、加噪声
-
Dropout(随机屏蔽神经元)
-
L2 正则化(weight decay)
-
降低模型容量(减少层数或参数)
-
早停 Early stopping
-
增加训练数据
6.2 欠拟合
训练集上的效果都不好 ------ 模型太弱或训练不足
7. 梯度下降
梯度 = 多变量函数的"方向导数",代表函数增长最快的方向。
7.1 深度学习中的梯度
深度学习的目标是让损失函数 L(θ) 尽可能小 ,
这里 θ 是所有模型参数(权重)。
L(θ):
-
高 → 模型表现差
-
低 → 模型表现好
每次训练的关键是:
找到 L(θ) 下降最快的方向。
损失函数下降最快的方向 = 负梯度方向 −∇L(θ)
这就是"梯度下降"(Gradient Descent)。
7.2 梯度下降如何优化模型?
梯度告诉模型:参数往哪个方向改会让损失变小。
每一步更新:
θ=θ−η⋅∇L(θ)
其中
-
θ:模型参数
-
η:学习率
-
∇L:梯度
理解:
-
如果梯度很大 → 表示"损失增加得很快" → 用大步来修正
-
如果梯度很小 → 表示"接近最低点" → 用小步修正
最终,参数会"走向山谷底"(最优点)。
沿着 负梯度方向 能让损失函数下降得最快,最终找到最小值附近的点。
8.实践
框架
python
import numpy as np
import matplotlib.pyplot as plt
# ================================
# 1. 生成数据
# ================================
# y = 3x + 1,加上一点随机噪声会更真实
# TODO:生成 100 个 x 数据(建议使用 np.linspace)
# x = ?
# TODO:生成 y 数据(y = 3x + 1 + 噪声)
# y = ?
# ================================
# 2. 初始化参数
# ================================
# TODO:初始化 w 和 b(随机数即可,例如 0)
# w = ?
# b = ?
learning_rate = 0.01
epoch = 200
loss_history = []
# ================================
# 3. 定义预测函数
# ================================
def predict(x, w, b):
# TODO:返回 wx + b
# return ?
pass
# ================================
# 4. 定义损失函数(MSE)
# ================================
def compute_loss(y_pred, y_true):
# TODO:写出均方误差 MSE
# return ?
pass
# ================================
# 5. 手写计算梯度
# ================================
def compute_gradients(x, y_true, y_pred):
# TODO:
# ∂L/∂w = (2/n) * sum( x * (y_pred - y_true) )
# ∂L/∂b = (2/n) * sum( y_pred - y_true )
# return dw, db
pass
# ================================
# 6. 梯度下降循环
# ================================
for i in range(epoch):
# TODO:预测
# y_pred = ?
# TODO:计算损失
# loss = ?
# loss_history.append(loss)
# TODO:计算梯度
# dw, db = ?
# TODO:更新参数
# w = ?
# b = ?
# 每 20 次打印一次当前参数
if i % 20 == 0:
print(f"Epoch {i}: loss={loss:.4f}, w={w:.4f}, b={b:.4f}")
# ================================
# 7. 绘制损失下降曲线
# ================================
plt.plot(loss_history)
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.title("Loss Curve")
plt.show()
print("Final w =", w)
print("Final b =", b)
python
import numpy as np
import matplotlib.pyplot as plt
# ================================
# 1. 生成数据
# ================================
# y = 3x + 1,加上一点随机噪声会更真实
# TODO:生成 100 个 x 数据(建议使用 np.linspace)
x = np.linspace(0,10,100)
# TODO:生成 y 数据(y = 3x + 1 + 噪声)
y =3*x+1 + np.random.normal(0,1,100)
# ================================
# 2. 初始化参数
# ================================
# TODO:初始化 w 和 b(随机数即可,例如 0)
w = 0.0
b = 0.0
learning_rate = 0.01
epoch = 200
loss_history = []
# ================================
# 3. 定义预测函数
# ================================
def predict(x, w, b):
# TODO:返回 wx + b
return w*x+b
pass
# ================================
# 4. 定义损失函数(MSE)
# ================================
def compute_loss(y_pred, y_true):
# TODO:写出均方误差 MSE
return np.mean((y_pred-y_true)**2)
pass
# ================================
# 5. 手写计算梯度
# ================================
def compute_gradients(x, y_true, y_pred):
# TODO:
# ∂L/∂w = (2/n) * sum( x * (y_pred - y_true) )
# ∂L/∂b = (2/n) * sum( y_pred - y_true )
n=x.shape[0]
dw=(2/n)*sum(x*(y_pred - y_true))
db=(2/n)*sum((y_pred - y_true))
return dw, db
pass
# ================================
# 6. 梯度下降循环
# ================================
for i in range(epoch):
# TODO:预测
y_pred = predict(x, w, b)
# TODO:计算损失
loss = compute_loss(y_pred, y)
loss_history.append(loss)
# TODO:计算梯度
dw, db = compute_gradients(x, y, y_pred)
# TODO:更新参数
w = w-learning_rate*dw
b = b-learning_rate*db
# 每 20 次打印一次当前参数
if i % 20 == 0:
print(f"Epoch {i}: loss={loss:.4f}, w={w:.4f}, b={b:.4f}")
# ================================
# 7. 绘制损失下降曲线
# ================================
plt.plot(loss_history)
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.title("Loss Curve")
plt.show()
print("Final w =", w)
print("Final b =", b)