本博客的图表来源于《Dynamic UAV path planning in mountainous terrain utilizing an arithmetic optimization algorithm incorporating adaptive thermal conduction search and elite population genetic strategies》论文的实验数据
这篇发表于《Aerospace Science and Technology》(航空航天科学与技术领域的高水平期刊,JCR Q1区,最新影响因子5.63)的论文,提出了一种名为TQGAOA的改进算法,专门用于解决山区复杂地形下无人机动态路径规划的难题。
一、论文核心贡献与问题背景
论文致力于解决山区环境下无人机动态路径规划的挑战。这些挑战主要来自:
复杂地形:陡峭山脊、深谷等地形特征,极大地增加了飞行路径规划和风险。
动态障碍物:鸟类、其他无人机等动态障碍,要求无人机能够实时规避并调整路径。
多约束目标:路径规划需同时兼顾飞行安全、能量效率、监控区域覆盖率以及飞行高
传统路径规划方法(如RRT、A*、APF、深度学习等)在动态、复杂环境中表现不佳:
容易陷入局部最优;难以实时响应动态障碍;缺乏对多目标(能耗、安全、覆盖率)的综合考虑。
针对这些问题,论文的主要贡献在于提出了一种融合了三种改进策略的算术优化算法(AOA)新变体------TQGAOA,以提升算法在解决此类复杂优化问题时的综合性能。
二、动态路径规划数学模型详解
论文将无人机动态路径规划问题构建为一个多约束优化问题,其核心是如下总成本函数:
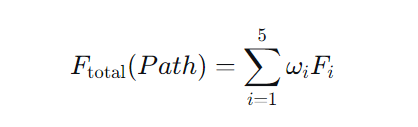
其中, 是各子成本函数的权重,用于根据不同任务需求调整其重要性。该总成本函数包含以下五个子成本函数:
能耗成本确保路径总长度、每一步到目标点的剩余距离以及总步数尽可能小,以节省能量
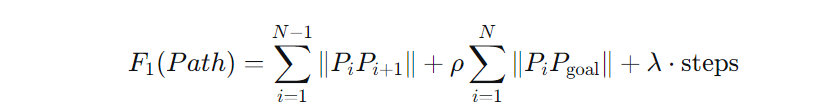
第一项:路径总长度
第二项:引导无人机朝向目标
第三项:惩罚步数过多
障碍威胁成本迫使无人机与静态、动态障碍物保持安全距离。动态障碍物位置会根据预设轨迹实时更新。
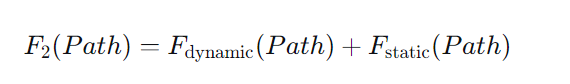
对静态和动态障碍分别建模为圆柱体
动态障碍位置随时间更新:
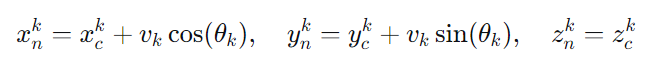
威胁成本函数为分段函数,根据距离决定是否碰撞、是否在安全距离内。
地形碰撞威胁成本通过三次样条插值在路径节点间插入密集点,检查是否与地形高程模型碰撞。
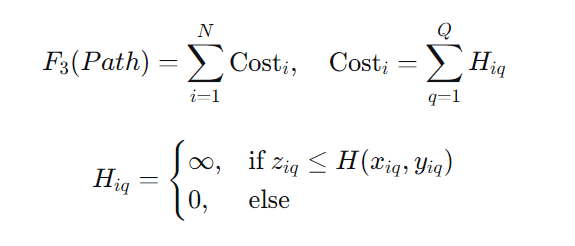
区域覆盖率成本鼓励无人机航迹尽可能覆盖任务区域,减少监测盲区。
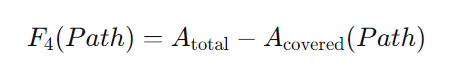
将任务区域划分为网格,计算未覆盖的网格数。
飞行高度成本 将无人机飞行高度约束在一个预设的安全范围内

论文中TQGAOA算法核心改进策略
基础AOA算法
AOA是元启发式算法的经典代表,由Abualigah及其团队于2021年提出。它采用了基本的算术运算------乘法、除法、加法和减法------来解决优化问题。AOA算法在更新候选解的迭代过程中具有数学上的可解释性,这为其在复杂受限环境中的优化搜索提供了更强的逻辑。此外,其结构简单且更新机制透明,使其极具未来研究者的改进和实用适应性。迄今为止,AOA已被广泛应用于解决各种工程优化挑战。
基于四种算术运算(加减乘除)的元启发式算法
分为探索阶段 (乘除)和开发阶段(加减)
使用 MOAMOA 函数控制阶段切换:
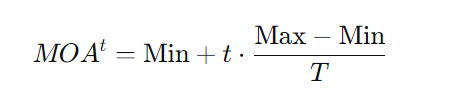
TQGAOA算法在基础AOA上集成了三种策略,显著提升了全局探索和局部开发能力:
自适应热传导搜索策略 (Exploration阶段增强)
灵感来源:物理中的热传导现象,热量从高温物体传向低温物体。
核心机制:将当前解与最优解的差异视为"温度差":
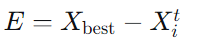
热传导效率自适应变化:
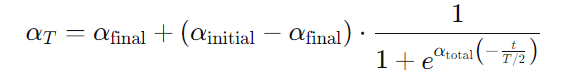
引入t分布扰动

模拟异常热传导,帮助算法跳出局部最优。
作用:在迭代前期, 较大,扰动强,增强全局探索;迭代后期,
减小,进行精细局部搜索。
二次插值策略 (Exploitation阶段增强)
灵感来源:数学中的曲线拟合方法。
核心机制:利用当前最优解和两个随机解的信息,构造二次插值曲线,预测出潜在更优的新解位置。其数学表达式为:
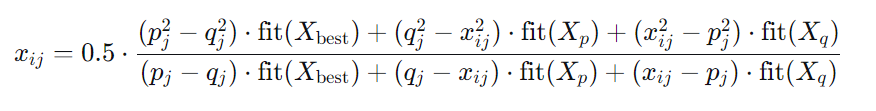
作用:使算法在局部开发时更新机制更精细,避免因过度依赖单一最优解而陷入局部最优。
精英种群遗传策略
灵感来源:遗传算法中的交叉和变异操作。
核心机制:
精英选择:选取种群中适应度最高的前三个解作为精英解。
交叉操作:精英解与其他解进行信息交换,生成新解:
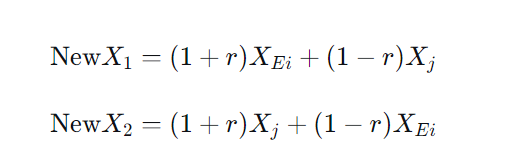
变异操作:以较小概率(论文设为0.05)随机改变解的某些维度,增加种群多样性:
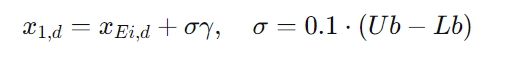
作用:促进优质信息在种群中传播,同时通过变异维持种群多样性,防止早熟收敛。
这三种策略的协作关系如下所示:
自适应热传导搜索进行全局探索 可以扩大搜索范围,避免早熟收敛
二次插值进行局部开发提高局部搜索精度和收敛速度
精英种群遗传进行种群更新可以保持种群多样性,促进优质信息交流
三、实验验证与性能分析
论文通过标准函数测试和路径规划实验验证TQGAOA的性能。
CEC2017基准测试
在复杂的优化问题中,算法性能的评估至关重要,尤其是在处理高维和多约束问题时。CEC2017基准测试集被广泛用于优化算法的比较研究,涵盖了多种优化问题类型。本节基于该标准基准,全面评估TQGAOA算法在不同优化任务中的性能,为其在无人机路径规划问题中的应用奠定理论基础。

对比算法:与JAYA、DE、IVY、BKA、GWOCS、MPSO、TSLSSCSO及原始AOA等8种元启发式算法对比。
关键结果:在29个测试函数中,TQGAOA在19个函数上取得最优平均解,展现出更强的收敛精度和鲁棒性。在某些函数上,其精度较原始AOA提升了七个数量级。TQGAOA在函数方面展现出明显优势F1,F3,F10,F12,F14,F16,F18,F28 和F29其雷达图表曲线显著向中心收缩,呈现更紧凑稳定的形状。相比之下,AOA、TSLSSCSO和JAYA等算法在多函数上表现较差,外扩轮廓反映收敛能力较弱。
统计检验:Wilcoxon符号秩检验结果表明TQGAOA相比大多数对比算法具有显著性能优势。
山区路径规划实验
场景设置:基于真实山区地形(天津蓟州区许家台镇)构建了6个不同复杂度的场景,障碍物密度和动态障碍比例递增。
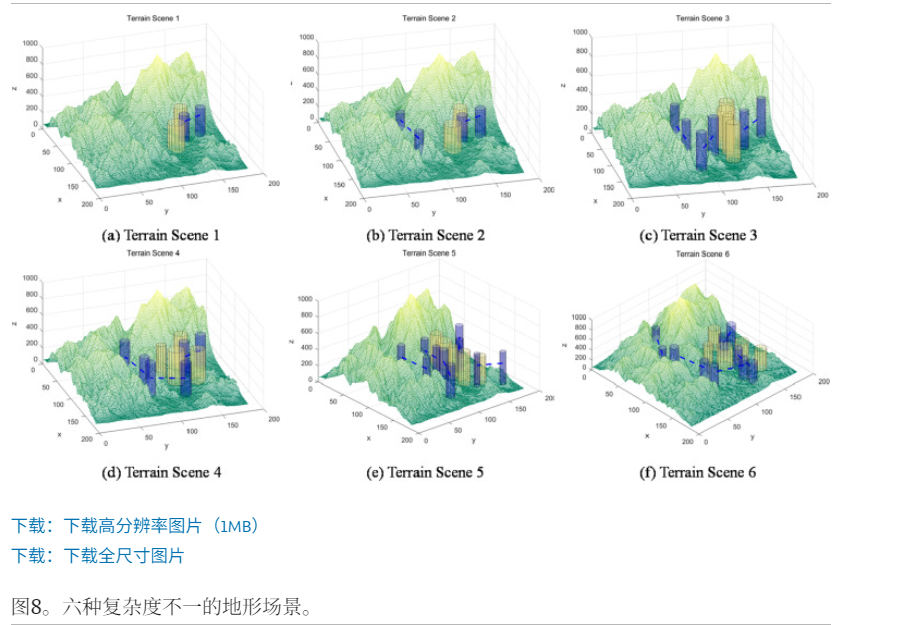
评估指标:路径总成本、成本标准差(稳定性)、规划所需平均步数。
关键结果:
TQGAOA在所有6种场景下均取得最低的平均路径成本。
在5种场景下取得了最小的标准差,表明其规划结果稳定性高、可重复性好。
所需平均步数最少,意味着路径更直接、能量更高效。
可视化路径图显示,TQGAOA规划的路径更短、更平滑,且能有效覆盖任务核心监测区域。
消融实验与参数分析
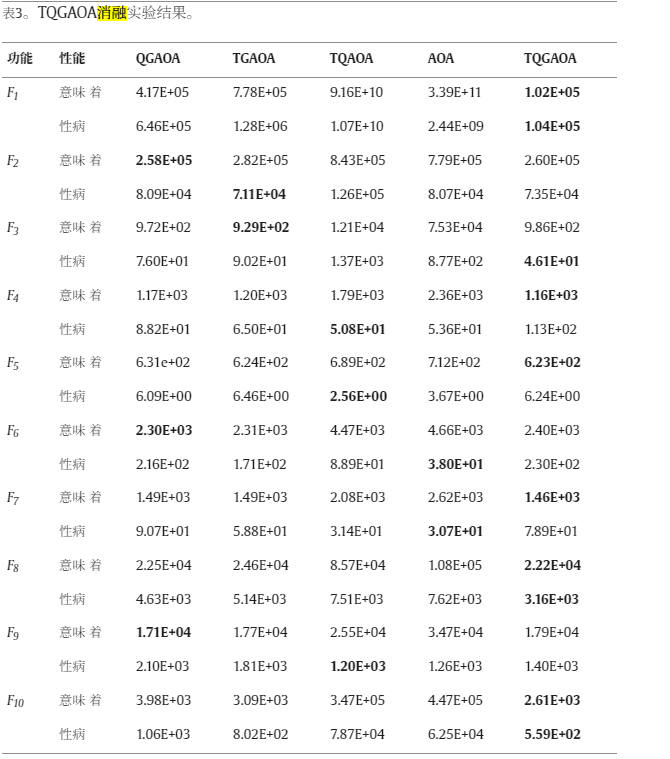
消融实验:通过逐一移除三个改进策略,验证了每个策略对算法性能提升均有贡献,且三者具有互补性。
参数敏感性分析:确定了自适应热传导搜索策略中参数和
为较优配置。
在平均表现方面,TQGAOA在六个函数情形中取得最佳成绩,而QGAOA和TGAOA分别在三种和一种情况下表现最佳。将QGAOA与完整的TQGAOA进行比较,可以发现F1,F5,F7,F8 和F10这些都是单模或多模函数,去除该策略后性能显著下降。这表明自适应热传导搜索有效扩大了全球勘探阶段的搜索范围,防止过早收敛。
TGAOA在所有功能上表现都不如TQGAOA,除了F3 ,其中性能差距特别大F1,F8 和F10.F1是一个单峰函数,主要考察算法的局部搜索能力,而 TGAOA 和 TQGAOA 之间最大的区别就在这里。这表明二次插值策略提高了局部利用阶段的搜索精度,使候选解在接近最优解时能做出更细致的调整,从而提高收敛准确性。
四、论文总结与未来展望
这项研究针对山区复杂环境下的无人机动态路径规划问题,提出了一种集成多策略改进的TQGAOA算法,核心价值在于:
有效性:通过精确的数学模型将复杂的工程问题转化为多目标优化问题。
创新性:将自适应热传导搜索、二次插值和精英种群遗传策略有机结合,有效平衡了全局探索和局部开发。
实用性:在标准测试和模拟场景中均表现出更优的路径质量、收敛性和鲁棒性。
论文也指出了当前研究的局限性和未来方向:
局限性:未考虑完整的无人机动力学和电池消耗模型;动态障碍物运动模式假设过于理想;算法计算时间略长(但仍处于秒级,可接受)。
未来方向:集成更精确的无人机物理模型;研究动态障碍物的不确定性建模;将算法扩展到多无人机协同路径规划任务;进行实际外场飞行验证。