方法三:贪心枚举
递归解决方法为我们理解问题提供了简洁直观的方法。我们仍然可以用递归解决这个问题。为了改进上述暴力枚举解决方案,我们可以在递归中加入贪心。我们可以将枚举重新格式化如下:
从一个数字到多个数字的组合开始,一旦我们找到一个可以组合成给定数字 n 的组合。
那么我们可以说我们找到了最小的组合,因为我们贪心的从小到大的枚举组合。
为了更好的解释,我们首先定义一个名为 is_divided_by(n, count) 的函数,该函数返回一个布尔值,表示数字 n是否可以被一个数字 count 组合,而不是像前面函数 numSquares(n) 返回组合的确切大小。
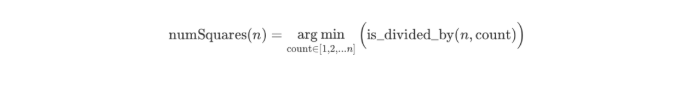
与递归函数 numSquare(n) 不同,is_divided_by(n, count) 的递归过程可以归结为底部情况(即 count==1)更快。
下面是一个关于函数 is_divided_by(n, count) 的例子,它对 输入 n=5 和 count=2 进行了分解。
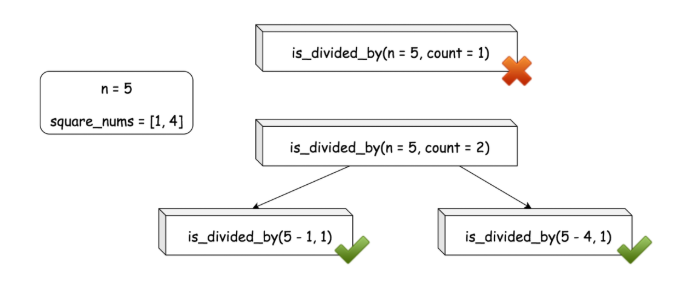
通过这种重新构造的技巧,我们可以显著降低堆栈溢出的风险。