Flutter for OpenHarmony 实现计算几何：Graham Scan 凸包算法的可视化演示

Flutter for OpenHarmony 实现计算几何：Graham Scan 凸包算法的可视化演示

在计算几何学中，凸包问题是一个基础且重要的研究领域。它不仅具有理论意义，在计算机图形学、地理信息系统（GIS）、机器人路径规划等领域也有广泛应用。本文将通过一段完整的 Flutter 代码示例，展示如何利用 Graham Scan 算法实现二维点集的凸包计算，并以直观的 UI 展示其形成过程。

🌐 加入社区 欢迎加入 开源鸿蒙跨平台开发者社区 ，获取最新资源与技术支持： 👉 开源鸿蒙跨平台开发者社区

---

完整效果

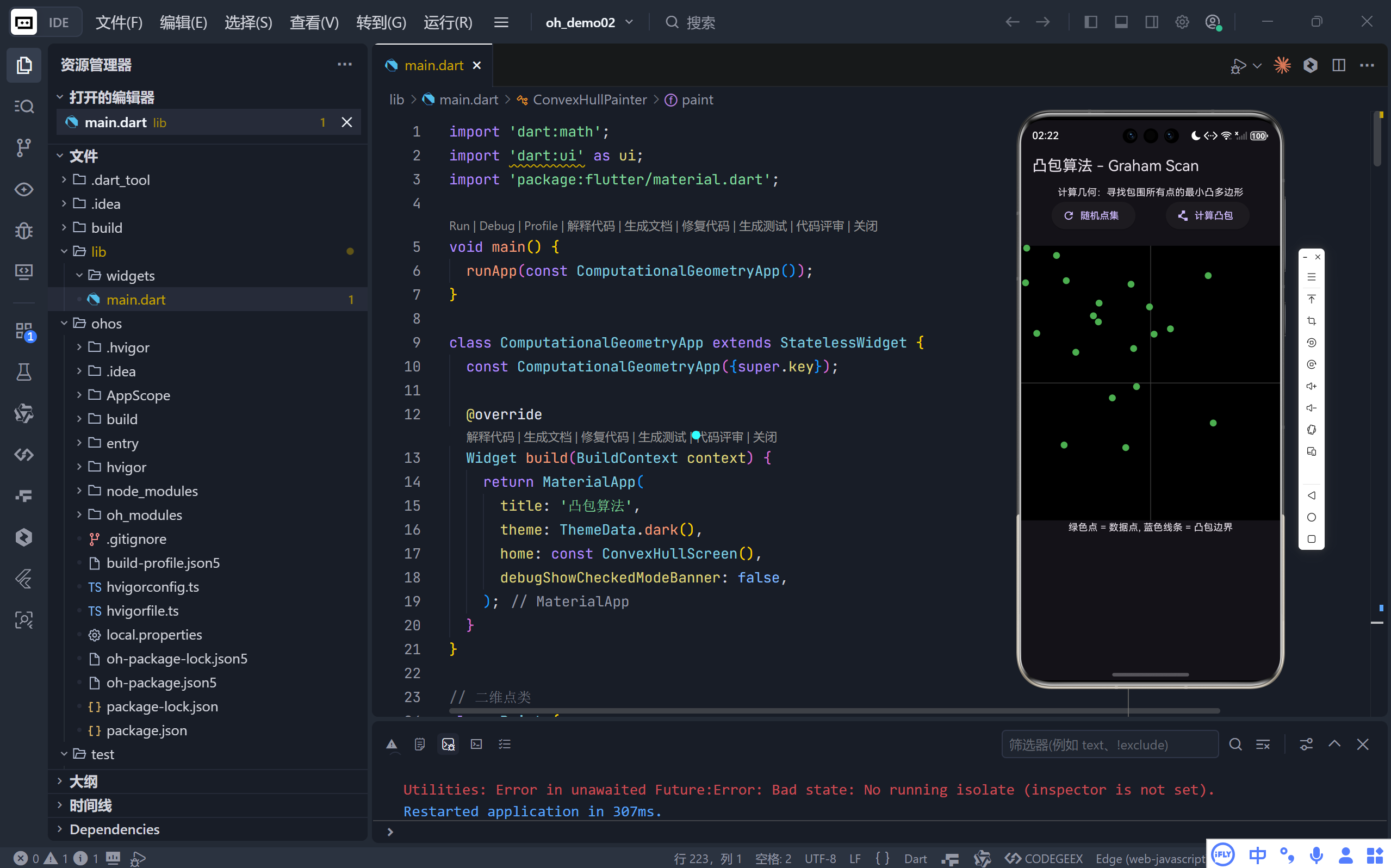
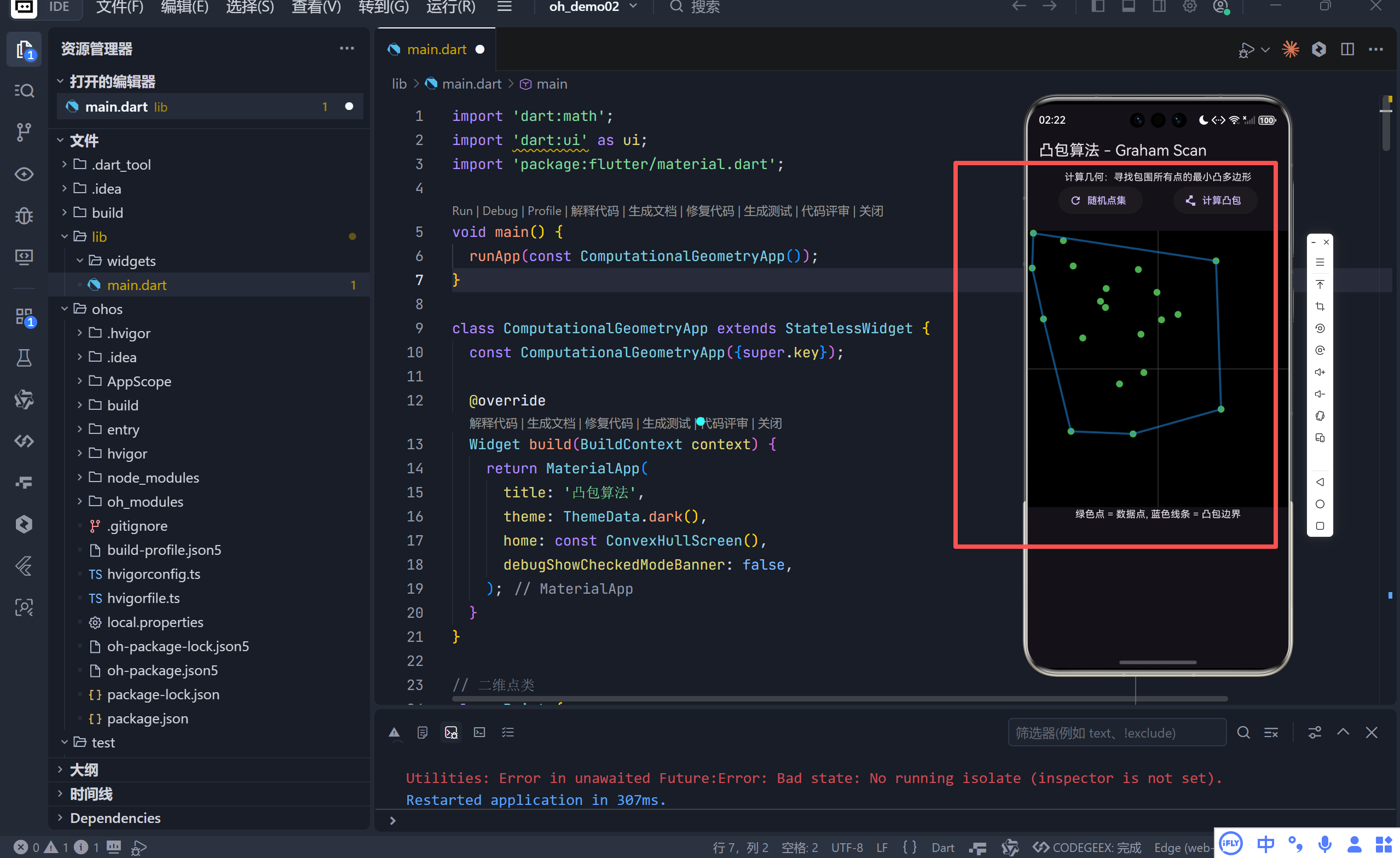
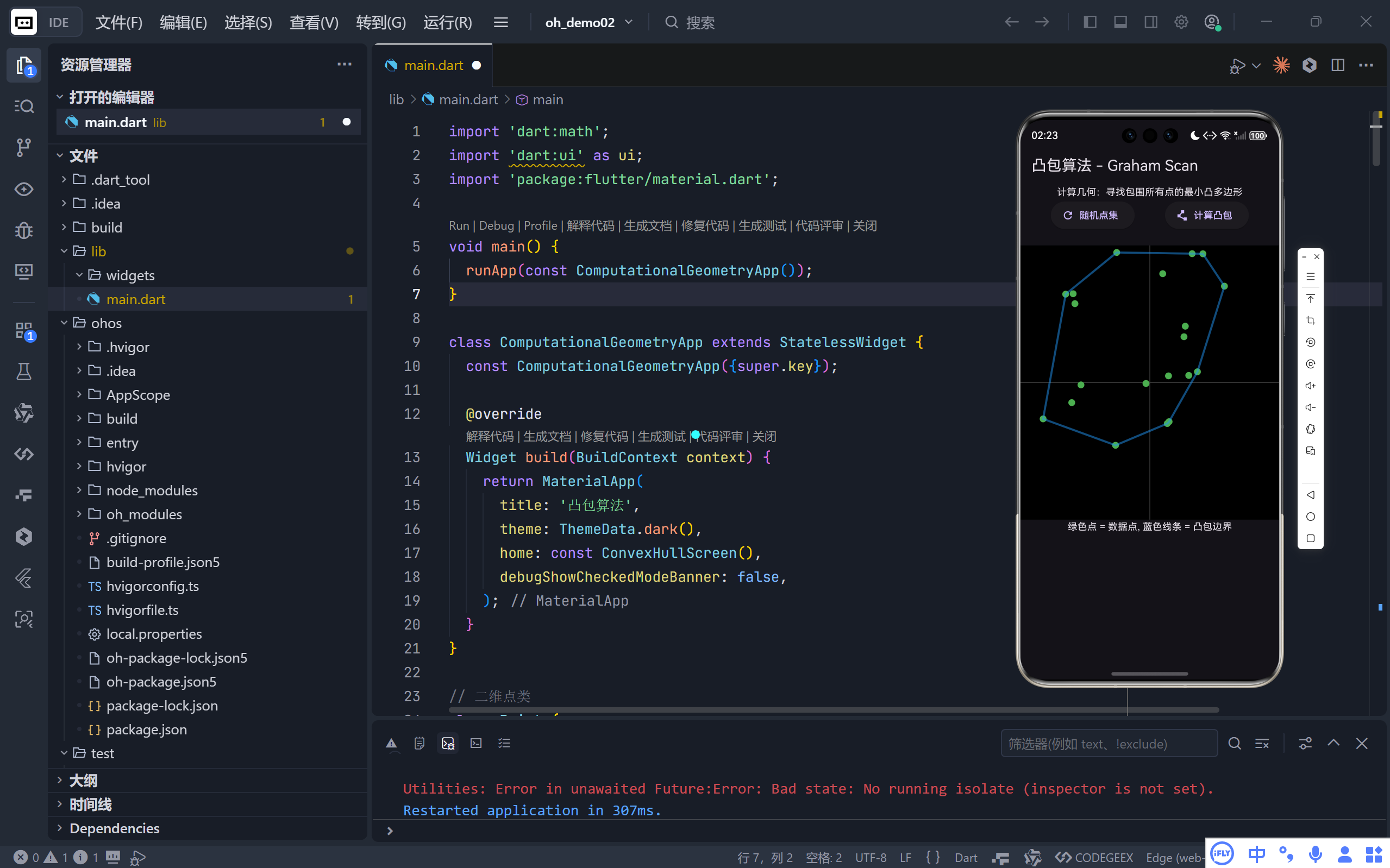
一、项目概述

应用功能

该应用主要实现了以下功能：

• 自动生成随机分布的二维点集；
• 使用 Graham Scan 算法计算并显示这些点的最小凸多边形（即凸包）；
• 动态展示凸包构建的过程，增强用户对算法的理解。

核心技术

• Dart：Flutter 的编程语言，用于编写逻辑和界面。
• Graham Scan 算法：一种高效计算平面点集凸包的经典算法，时间复杂度为 O(n log n)。
• CustomPaint 组件：Flutter 中绘制自定义图形的关键组件。

---

二、Graham Scan 算法详解

1. 基本思想

Graham Scan 通过如下步骤找到点集的凸包：

1. 选择基准点：通常选取 y 坐标最小的点作为起点（如果存在多个这样的点，则选 x 坐标最小者）。
2. 排序剩余点：基于与基准点的极角大小对其他点进行排序；若角度相同，则距离近者优先。
3. 构造栈结构：遍历排序后的点集，使用栈维护当前凸包边界上的点，确保每增加一个新点时，形成的转向均为左转（逆时针方向），否则移除栈顶元素直至满足条件。

2. 关键函数解释

// 计算叉积 (判断转向)
double _crossProduct(Point o, Point a, Point b) {
  return (a.x - o.x) * (b.y - o.y) - (a.y - o.y) * (b.x - o.x);
}

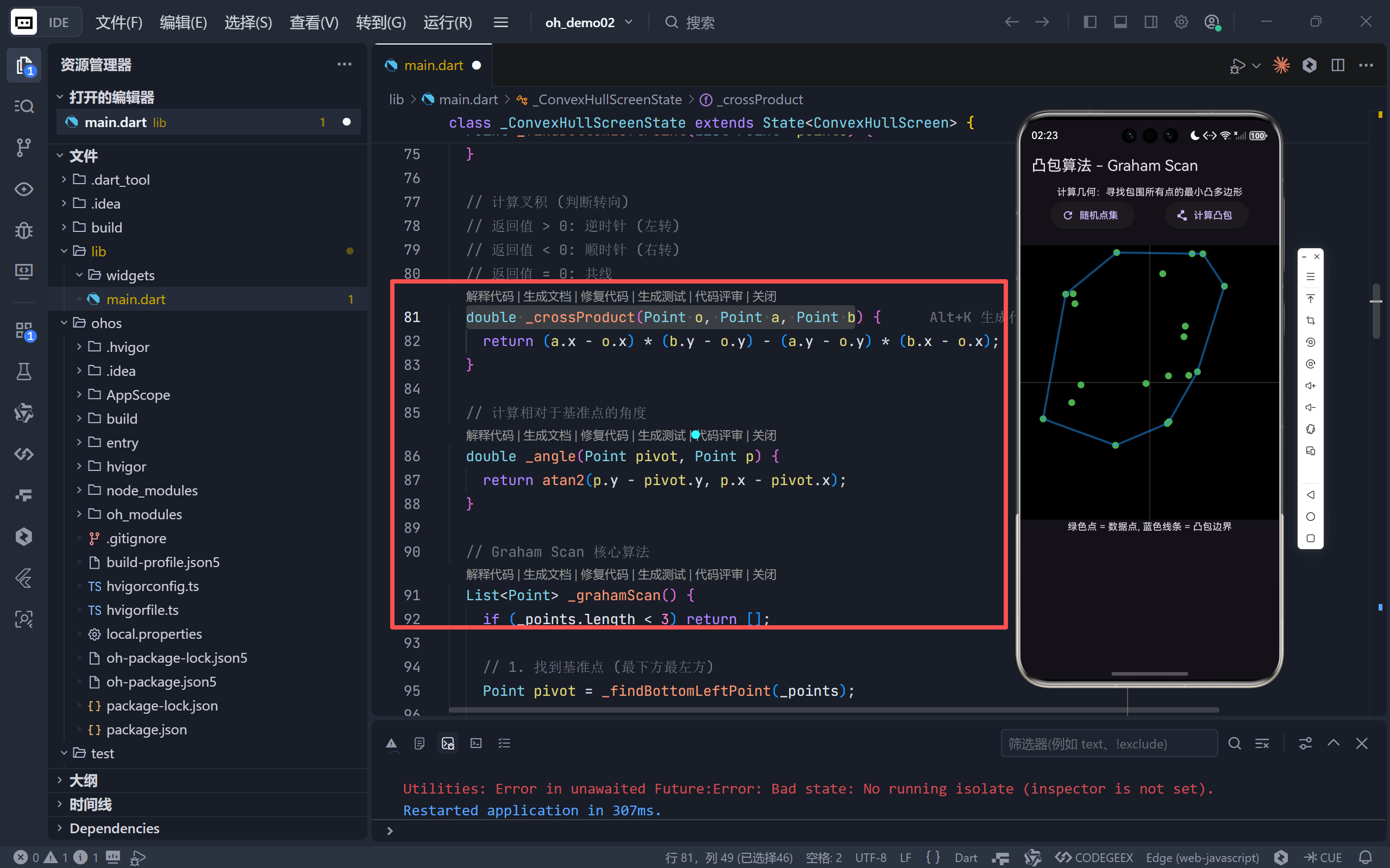
此函数用于判断三个点 o, a, b 形成的方向。正数表示左转，负数表示右转，零则代表三点共线。

// 按照相对于基准点的角度进行排序
List<Point> sortedPoints = List.from(_points);
sortedPoints.sort((a, b) {
  double angleA = _angle(pivot, a);
  double angleB = _angle(pivot, b);
  if (angleA == angleB) {
    // 如果角度相同，距离近的排在前面
    return pivot.distanceTo(a).compareTo(pivot.distanceTo(b));
  }
  return angleA.compareTo(angleB);
});

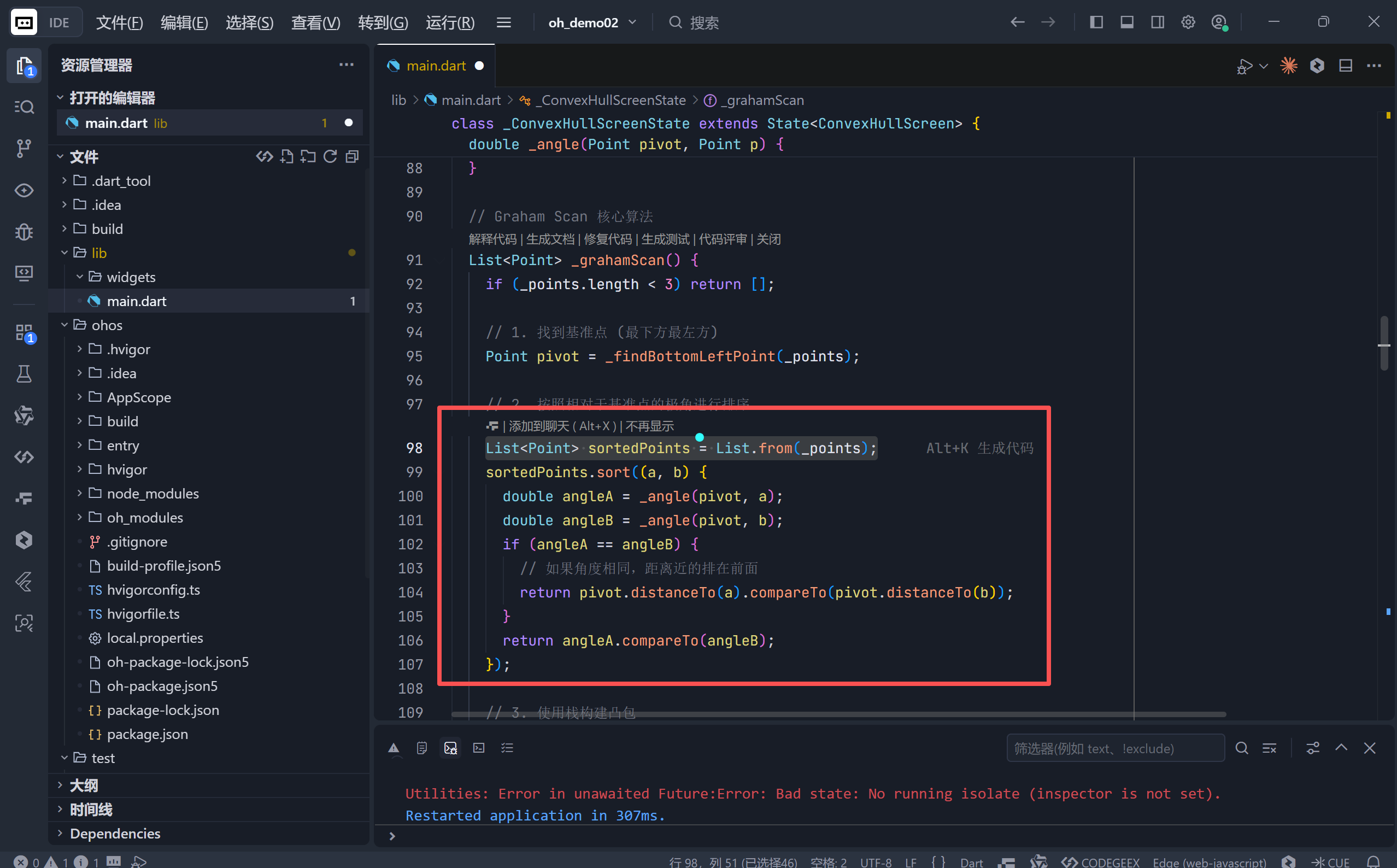
这里首先计算每个点相对于基准点的角度，然后根据角度大小排序，处理特殊情况（如角度相同时按距离排序）。

---

三、UI 设计与交互体验

1. 主界面布局

• 顶部操作区：包含两个按钮------"随机点集"用于重新生成点，"计算凸包"触发 Graham Scan 算法执行。
• 绘图区域 ：采用 CustomPaint 组件动态绘制点集及其凸包边界。绿色圆点代表原始数据点，蓝色线条描绘最终形成的凸包轮廓。
• 提示信息：简要说明各颜色标记的意义，帮助用户理解界面元素。

2. 动态效果

为了增强教学效果，每当点击"计算凸包"按钮后，程序会模拟一定延迟，逐步显示出凸包构建的全过程。这不仅让抽象的数学运算变得生动具体，也加深了对算法流程的认识。

---

四、代码亮点分析

1. 数据结构设计

class Point {
  final double x, y;
  Point(this.x, this.y);

  double distanceTo(Point other) {
    return sqrt(pow(x - other.x, 2) + pow(y - other.y, 2));
  }
}

简洁明了地定义了二维点类，内含坐标属性及两点间距离计算方法，便于后续调用。

2. 异步处理

void _computeHull() async {
  ...
  await Future.delayed(const Duration(milliseconds: 500));
  ...
  for (int i = 0; i <= hull.length; i++) {
    ...
    await Future.delayed(const Duration(milliseconds: 300));
  }
}

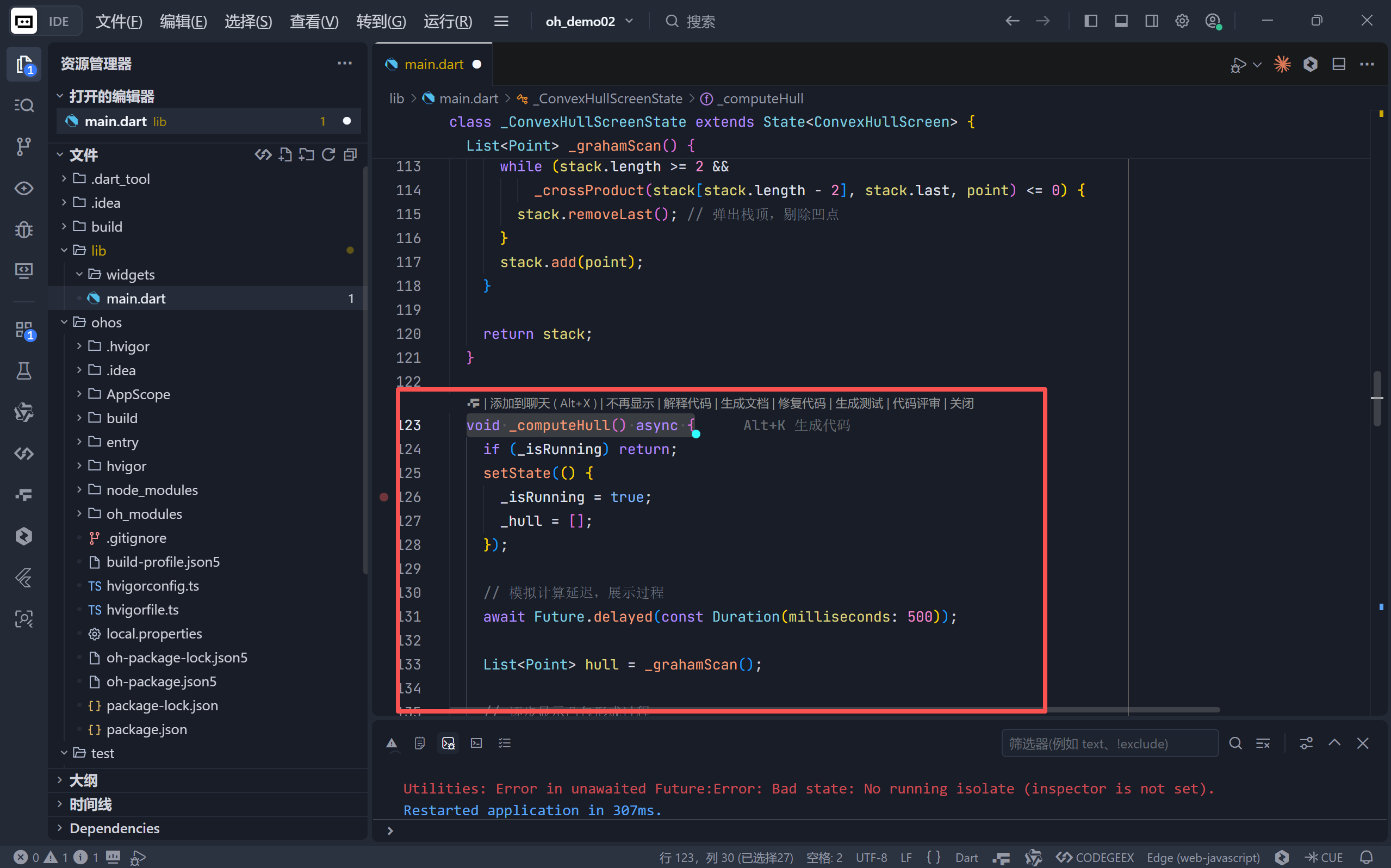
通过异步函数结合延时器，巧妙实现了动画效果，使凸包形成过程得以分步呈现。

---

五、结论与展望

通过这段 Flutter 应用，我们不仅能深入理解 Graham Scan 算法的工作原理，还能领略到计算几何的魅力所在。尽管这里的实现针对的是简单的二维空间，但其所蕴含的思想同样适用于更高维度的问题求解。未来可以考虑加入更多类型的计算几何算法，进一步丰富学习资源，或集成实际应用场景的数据集，提升实用性。

完整代码

import 'dart:math';
import 'dart:ui' as ui;
import 'package:flutter/material.dart';

void main() {
  runApp(const ComputationalGeometryApp());
}

class ComputationalGeometryApp extends StatelessWidget {
  const ComputationalGeometryApp({super.key});

  @override
  Widget build(BuildContext context) {
    return MaterialApp(
      title: '凸包算法',
      theme: ThemeData.dark(),
      home: const ConvexHullScreen(),
      debugShowCheckedModeBanner: false,
    );
  }
}

// 二维点类
class Point {
  final double x, y;
  Point(this.x, this.y);

  // 计算两点之间的距离
  double distanceTo(Point other) {
    return sqrt(pow(x - other.x, 2) + pow(y - other.y, 2));
  }
}

class ConvexHullScreen extends StatefulWidget {
  const ConvexHullScreen({super.key});

  @override
  State<ConvexHullScreen> createState() => _ConvexHullScreenState();
}

class _ConvexHullScreenState extends State<ConvexHullScreen> {
  List<Point> _points = [];
  List<Point> _hull = [];
  bool _isRunning = false;

  @override
  void initState() {
    super.initState();
    _generateRandomPoints();
  }

  // 生成随机点
  void _generateRandomPoints() {
    final random = Random();
    setState(() {
      _points = List.generate(20, (index) {
        return Point(
          random.nextDouble() * 300,
          random.nextDouble() * 300,
        );
      });
      _hull = [];
    });
  }

  // 寻找最下方（最左方）的点作为基准点
  Point _findBottomLeftPoint(List<Point> points) {
    Point bottomLeft = points[0];
    for (Point p in points) {
      if (p.y < bottomLeft.y || (p.y == bottomLeft.y && p.x < bottomLeft.x)) {
        bottomLeft = p;
      }
    }
    return bottomLeft;
  }

  // 计算叉积 (判断转向)
  // 返回值 > 0: 逆时针 (左转)
  // 返回值 < 0: 顺时针 (右转)
  // 返回值 = 0: 共线
  double _crossProduct(Point o, Point a, Point b) {
    return (a.x - o.x) * (b.y - o.y) - (a.y - o.y) * (b.x - o.x);
  }

  // 计算相对于基准点的角度
  double _angle(Point pivot, Point p) {
    return atan2(p.y - pivot.y, p.x - pivot.x);
  }

  // Graham Scan 核心算法
  List<Point> _grahamScan() {
    if (_points.length < 3) return [];

    // 1. 找到基准点 (最下方最左方)
    Point pivot = _findBottomLeftPoint(_points);

    // 2. 按照相对于基准点的极角进行排序
    List<Point> sortedPoints = List.from(_points);
    sortedPoints.sort((a, b) {
      double angleA = _angle(pivot, a);
      double angleB = _angle(pivot, b);
      if (angleA == angleB) {
        // 如果角度相同，距离近的排在前面
        return pivot.distanceTo(a).compareTo(pivot.distanceTo(b));
      }
      return angleA.compareTo(angleB);
    });

    // 3. 使用栈构建凸包
    List<Point> stack = [];
    for (Point point in sortedPoints) {
      // 如果栈中至少有两个点，检查是否为右转
      while (stack.length >= 2 &&
          _crossProduct(stack[stack.length - 2], stack.last, point) <= 0) {
        stack.removeLast(); // 弹出栈顶，剔除凹点
      }
      stack.add(point);
    }

    return stack;
  }

  void _computeHull() async {
    if (_isRunning) return;
    setState(() {
      _isRunning = true;
      _hull = [];
    });

    // 模拟计算延迟，展示过程
    await Future.delayed(const Duration(milliseconds: 500));

    List<Point> hull = _grahamScan();

    // 逐步显示凸包形成过程
    for (int i = 0; i <= hull.length; i++) {
      if (!_isRunning) break;
      setState(() {
        _hull = hull.sublist(0, i);
      });
      await Future.delayed(const Duration(milliseconds: 300));
    }

    setState(() {
      _isRunning = false;
    });
  }

  @override
  Widget build(BuildContext context) {
    return Scaffold(
      appBar: AppBar(
        title: const Text('凸包算法 - Graham Scan'),
      ),
      body: Column(
        children: [
          const Text('计算几何：寻找包围所有点的最小凸多边形'),
          Row(
            mainAxisAlignment: MainAxisAlignment.spaceEvenly,
            children: [
              ElevatedButton.icon(
                onPressed: _generateRandomPoints,
                icon: const Icon(Icons.refresh),
                label: const Text('随机点集'),
              ),
              ElevatedButton.icon(
                onPressed: _computeHull,
                icon: const Icon(Icons.polyline),
                label: Text(_isRunning ? '计算中...' : '计算凸包'),
              ),
            ],
          ),
          const SizedBox(height: 20),
          CustomPaint(
            size: const Size(400, 400),
            painter: ConvexHullPainter(_points, _hull),
          ),
          const Text('绿色点 = 数据点, 蓝色线条 = 凸包边界'),
        ],
      ),
    );
  }
}

class ConvexHullPainter extends CustomPainter {
  final List<Point> points;
  final List<Point> hull;

  ConvexHullPainter(this.points, this.hull);

  @override
  void paint(Canvas canvas, Size size) {
    final bgPaint = Paint()..color = Colors.black;
    canvas.drawRect(Rect.fromLTWH(0, 0, size.width, size.height), bgPaint);

    // 绘制坐标系背景 (可选)
    final axisPaint = Paint()
      ..color = Colors.grey[800]!
      ..strokeWidth = 1;
    canvas.drawLine(Offset(0, size.height / 2),
        Offset(size.width, size.height / 2), axisPaint);
    canvas.drawLine(Offset(size.width / 2, 0),
        Offset(size.width / 2, size.height), axisPaint);

    // 绘制所有数据点
    final pointPaint = Paint()
      ..color = Colors.green
      ..style = PaintingStyle.fill;
    for (var point in points) {
      canvas.drawCircle(Offset(point.x, point.y), 5, pointPaint);
    }

    // 绘制凸包连线
    if (hull.isNotEmpty) {
      final hullPaint = Paint()
        ..color = Colors.blue.withOpacity(0.5)
        ..style = PaintingStyle.stroke
        ..strokeWidth = 3
        ..strokeCap = StrokeCap.round;

      Path path = Path();
      path.moveTo(hull[0].x, hull[0].y);

      for (int i = 1; i < hull.length; i++) {
        path.lineTo(hull[i].x, hull[i].y);
      }

      // 如果凸包闭合，画回起点
      if (hull.length > 2) {
        path.close();
      }

      canvas.drawPath(path, hullPaint);
    }
  }

  @override
  bool shouldRepaint(covariant CustomPainter oldDelegate) => true;
}