模拟退火算法求解聚类问题python代码示例

一、模拟退火算法简介
- 1.1智能优化算法
- 1.2模拟退火算法原理
二、聚类问题
三、求解代码

一、模拟退火算法简介

1.1智能优化算法

模拟退火算法属于智能优化算法（Intelligent Optimization Algorithms）的一种，智能优化算法也被称为进化计算（Evolutionary Computation, EC）、群体智能算法（Swarm Intelligence Algorithms），属于优化算法大类，但不同于数学优化中的梯度下降、牛顿法，不是精确解法，不追求理论的严谨，而是模拟自然界的过程来寻找较优解。

禁忌搜索（Tabu Search或Taboo Search）、遗传算法（Genetic Algorithm, GA）、粒子群优化（Particle Swarm Optimization, PSO）都属于智能优化算法，常用于参数调优、组合优化（如旅行商问题 TSP）、工程设计优化、机器学习模型超参数搜索等。

1.2模拟退火算法原理

模拟退火（Simulated Annealing，SA）算法，源于对热力学中退火过程的模拟，随着温度的逐渐下降，以不同的概率接受邻域中的次优解，避免陷入局部最优，是对局部搜索算法的拓展。

模拟退火算法早在1953年就由Metropolis提出，但直到1983年，Kirkpatrick成功地将模拟退火算法应用到组合最优化问题中，才真正创建了现代的模拟退火算法。

二、聚类问题

2.1聚类算法

聚类是无监督学习中的一种常见算法，旨在将数据集分割成不同的类或簇，使得同一簇内的数据对象相似性尽可能大，而不同簇之间的差异性尽可能大。

聚类算法与分类算法的区别在于，分类算法通常需要使用带有标签的数据进行训练，而聚类算法只需要指定一些类别和相似度标准等超参数即可运行，一般无须训练。

2.2模糊C-均值聚类算法

模糊C-均值聚类（Fuzzy C-means，FCM）是目前比较流行的一种聚类方法。该方法使用了在欧几里得空间确

定数据点的几何贴近度的概念，它将数据分配到不同的类别，然后计算数据点对于各个类别的隶属度和到类中心的欧几里得距离，根据这两个值计算目标函数，以目标函数的值衡量聚类效果。

但FCM算法依赖于初始值的选择，对初值很敏感，如果初值选择不当则会收敛到局部最优值。

2.3问题描述

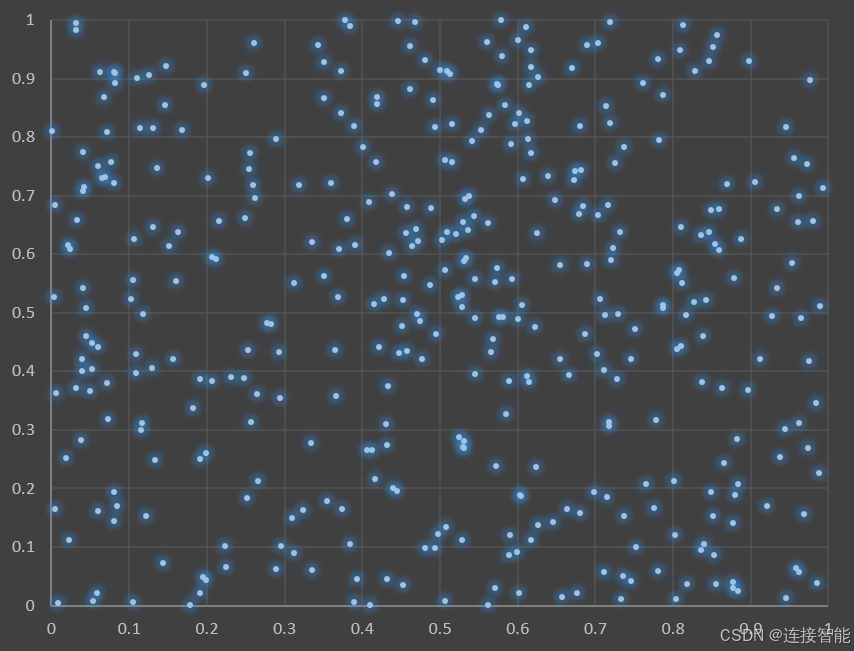
随机产生400个二维平面上的点，坐标取值区间为（0,1），假设这些点构成4个集合，点的分布如下图所示：

三、求解代码

3.1python实现代码

python 复制代码

import random
import sys
import numpy as np
from tqdm import tqdm
import matplotlib.pyplot as plt
import math
import random
import pandas as pd

def generate_inputData(inputData_num):
    inputData = np.random.random((inputData_num, 2))
    return inputData

def cluster_FCM(inputData, all_epoches, cluster_c, fcm_b):
    centers = inputData[np.random.choice(inputData.shape[0], cluster_c, replace = False)]
    min_goal = 1000
    min_center = np.zeros((cluster_c, 2))
    min_members = np.zeros((inputData.shape[0], cluster_c))
    for _ in range(all_epoches):
        distances = np.sum((inputData[:, np.newaxis] - centers) ** 2, axis = 2)
        distances[distances == 0] = 1e-6
        members = distances[:, :, np.newaxis] / distances[:, np.newaxis, :]
        members = 1 / np.sum(np.power(members, 1 / (fcm_b - 1)), axis = 2)
        goal_value = np.sum(distances * np.power(members, fcm_b))
        centers = np.sum((inputData[:, :, np.newaxis] * np.power(members, fcm_b)[:, np.newaxis, :]), axis = 0) / np.sum(np.power(members, fcm_b), axis = 0)
        centers = centers.T
        if goal_value < min_goal:
            min_goal = goal_value
            min_center = centers
            min_members = members
    
    return min_goal, min_center, min_members

def generate_originGroup(inputData, cluster_c, group_size):
    groups = np.zeros((group_size, cluster_c, 2))
    for i in range(group_size):
        groups[i] = inputData[np.random.choice(inputData.shape[0], cluster_c, replace = False)].copy()
    
    return groups

def calculate_goal_value(inputData, groups, fcm_b):
    distances = np.sum((inputData[np.newaxis, :, np.newaxis, :] - groups[:, np.newaxis, :, :]) ** 2, axis = 3)
    distances[distances == 0] = 1e-6
    
    members = distances[:, :, :, np.newaxis] / distances[:, :, np.newaxis, :]
    members = 1 / np.sum(np.power(members, 1 / (fcm_b - 1)), axis = 3)
    goal_value = np.sum(distances * np.power(members, fcm_b), axis = (1, 2))
    return goal_value, members, distances

def swap_random_bit_int(a, b):
    """随机交换两个整数的二进制位"""
    
    idx = random.randint(18, 23)  # 随机选择交换的二进制位索引
    # 获取对应的位
    bit_a = (a >> idx) & 1
    bit_b = (b >> idx) & 1
    # 如果两个位置不同，则交换
    if bit_a != bit_b:
        # 使用 XOR 交换两个位置的位
        a ^= (1 << idx)
        b ^= (1 << idx)
    
    return a, b

def flip_random_bit(a):
    """随机改变整数a的某一二进制位"""
    
    # 随机选择一个位索引
    idx = random.randint(18, 23)  # 随机选择一个索引
    
    # 通过 XOR 改变该位
    a ^= (1 << idx)  # 将a的第idx位翻转
    
    return a

def ga_cross_and_vary(groups, goal_value, ga_pc, ga_pm):
    new_groups = groups.copy()
    group_sort_index = np.argsort(goal_value)
    pc_num = int(new_groups.shape[0] * ga_pc)
    new_groups_int_rep = (new_groups * (2 ** 24)).astype(int)
    group_rand_num = new_groups.shape[1] * new_groups.shape[2]
    group_shape2 = new_groups.shape[2]
    for i in range(0, pc_num, 2):
        idx = np.random.randint(0, group_rand_num)
        shape1_idx, shape2_idx = divmod(idx, group_shape2)
        front_idx = group_sort_index[i]
        back_idx = group_sort_index[i + 1]
        tmp_a = new_groups_int_rep[front_idx, shape1_idx, shape2_idx]
        tmp_b = new_groups_int_rep[back_idx, shape1_idx, shape2_idx]
        new_groups_int_rep[front_idx, shape1_idx, shape2_idx], new_groups_int_rep[back_idx, shape1_idx, shape2_idx] = swap_random_bit_int(tmp_a, tmp_b)
    
    for i in range(pc_num, new_groups.shape[0]):
        idx = np.random.randint(0, group_rand_num)
        shape1_idx, shape2_idx = divmod(idx, group_shape2)
        front_idx = group_sort_index[i]
        tmp_a = new_groups_int_rep[front_idx, shape1_idx, shape2_idx]
        new_groups_int_rep[front_idx, shape1_idx, shape2_idx] = flip_random_bit(tmp_a)
    
    new_groups = new_groups_int_rep / (2 ** 24)
    return new_groups

def cluster_SAGA(inputData, ga_maxgen, cluster_c, fcm_b, group_size, ga_pc, ga_pm, sa_t0, sa_k, sa_tEnd):
    groups = generate_originGroup(inputData, cluster_c, group_size)
    min_goal = 1000
    min_center = np.zeros((cluster_c, 2))
    min_members = np.zeros((inputData.shape[0], cluster_c))
    sa_epoches = int(math.log(sa_tEnd / sa_t0, 10) / math.log(sa_k, 10)) + 1
    f = open('log_cluster.txt', 'w')
    for _ in tqdm(range(sa_epoches), position = 1):
        for _ in range(ga_maxgen):
            goal_value, members, _ = calculate_goal_value(inputData, groups, fcm_b)
            if goal_value.min() < min_goal:
                min_goal = goal_value.min()
                min_center = groups[goal_value.argmin()]
                min_members = members[goal_value.argmin()]
            
            new_groups = ga_cross_and_vary(groups, goal_value, ga_pc, ga_pm)
            
            new_goal_value, _, _ = calculate_goal_value(inputData, new_groups, fcm_b)
            probs = np.exp((goal_value - new_goal_value) / sa_t0)
            random_p = random.random()
            renew_groups = np.zeros(groups.shape)
            renew_groups[probs >= random_p] = new_groups[probs >= random_p].copy()
            renew_groups[probs < random_p] = groups[probs < random_p].copy()
            groups = renew_groups.copy()
        
        sa_t0 *= sa_k
        f.write(str(new_goal_value.min()))
        f.write('\n')
    
    f.close()
    return min_goal, min_center, min_members

def draw_points(inputData, centers, members):
    print(members[188])
    #print(members[202])
    tmp_dist = np.sum((inputData[188] - centers) ** 2, axis = 1)
    tmp_dist = tmp_dist.T
    tmp_mem = 1 / np.sum(np.power(tmp_dist[:, np.newaxis] / tmp_dist, 1 / 2), axis = 1)
    print(tmp_mem)
    members_max = np.argmax(members, axis = 1)
    data_group01 = inputData[members_max == 0]
    data_group02 = inputData[members_max == 1]
    data_group03 = inputData[members_max == 2]
    data_group04 = inputData[members_max == 3]
    plt.scatter(data_group01[:, 0], data_group01[:, 1], marker = 'o', color = 'blue', alpha = 0.7)
    plt.scatter(data_group02[:, 0], data_group02[:, 1], marker = 'o', color = 'lime', alpha = 0.7)
    plt.scatter(data_group03[:, 0], data_group03[:, 1], marker = 'o', color = 'yellow', alpha = 0.7)
    plt.scatter(data_group04[:, 0], data_group04[:, 1], marker = 'o', color = 'red', alpha = 0.7)
    plt.scatter(centers[0, 0], centers[0, 1], marker = 'D', color = 'black', alpha = 1)
    plt.scatter(centers[1, 0], centers[1, 1], marker = 'D', color = 'black', alpha = 1)
    plt.scatter(centers[2, 0], centers[2, 1], marker = 'D', color = 'black', alpha = 1)
    plt.scatter(centers[3, 0], centers[3, 1], marker = 'D', color = 'black', alpha = 1)
    plt.show()

if __name__ == '__main__':
    #inputData = generate_inputData(400)
    inputData = np.array(pd.read_excel('data_cluster.xlsx', header = None))
    #FCM算法
    all_epoches = 1000
    all_min_goal = 1000
    cluster_c = 4
    fcm_b = 3
    all_min_center = np.zeros((cluster_c, 2))
    all_min_members = np.zeros((inputData.shape[0], cluster_c))
    for _ in range(1):
        tmp_goal, tmp_min_center, tmp_min_members = cluster_FCM(inputData, all_epoches, cluster_c, fcm_b)
        if tmp_goal < all_min_goal:
            all_min_goal = tmp_goal
            all_min_center = tmp_min_center
            all_min_members = tmp_min_members
        
        print(tmp_goal)
    
    print(f"min goal is {all_min_goal}")
    np.save('min_fcm_center_cluster.npy', all_min_center)
    np.save('min_fcm_members_cluster.npy', all_min_members)
    sys.exit(0)
    
    #遗传加退火算法
    ga_maxgen = 20
    group_size = 200
    ga_pc = 0.8
    ga_pm = 0.2
    sa_t0 = 0.1
    sa_k = 0.9
    sa_tEnd = 1e-7
    for _ in tqdm(range(20), position = 5):
        tmp_goal, tmp_min_center, tmp_min_members = cluster_SAGA(inputData, ga_maxgen, cluster_c, fcm_b, group_size, ga_pc, ga_pm, sa_t0, sa_k, sa_tEnd)
        if tmp_goal < all_min_goal:
            all_min_goal = tmp_goal
            all_min_center = tmp_min_center
            all_min_members = tmp_min_members
    
    print(f"SAGA done with min goal value: {all_min_goal}, center is {all_min_center}")
    np.save('min_saga_center_cluster.npy', all_min_center)
    np.save('min_saga_members_cluster.npy', all_min_members)
    #draw_points(inputData, all_min_center, all_min_members)

3.2代码说明

上一节给出的代码实现了两种算法，分别为FCM算法和模拟退火算法与遗传算法结合优化FCM的算法，对两种算法的效果进行对比。

3.2.1FCM算法说明

FCM算法通过cluster_FCM函数实现，算法超参数为预设的类别数cluster_c，加权参数fcm_b以及总迭代次数all_epoches。

FCM算法目标函数计算公式如下：

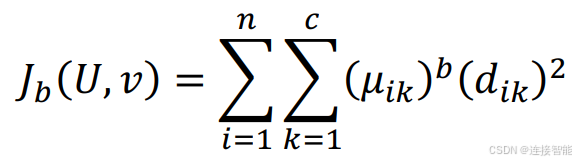
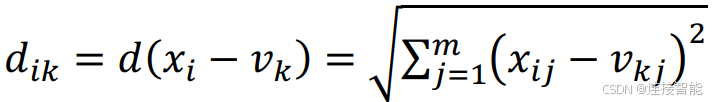
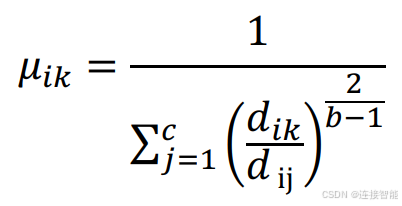
类中心的迭代计算公式为：

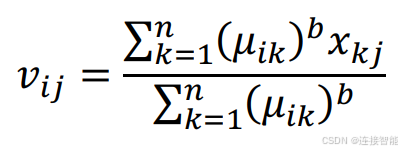
按照公式，函数逻辑如下

首先随机选择数据点中的4个点作为初始中心点，设置变量存储最小目标函数值等参数，进入循环；
按照上述公式计算每个点到4个中心点的距离，根据距离计算隶属度，根据距离和隶属度计算目标函数值；
按照公式根据隶属度值更新中心点坐标，然后进入下次循环，直至循环结束。

3.2.2模拟退火加遗传优化FCM算法说明

算法通过cluster_SAGA函数实现，由于单纯FCM算法受初始点选择的影响容易陷入局部最优，因此先使用遗传算法生成大量种群，每个个体就是一组FCM的初始中心点，种群进行选择交叉、变异等操作，对产生的子代计算目标函数值，函数值如果优于父代则替换掉父代，如果劣于父代，那么按照模拟退火算法的思想计算一个概率值，根据概论决定是否接受劣质子代替换掉父代。

算法超参数如下：

参数名称	参数值
遗传-种群数量	200
遗传-最大迭代次数	20
遗传-交叉概率	0.8
遗传-交叉方法	单点交叉
遗传-变异概率	0.2
退火-初始温度	0.1
退火-冷却系数	0.9
退火-终止温度	1e-7

函数逻辑如下：

首先通过函数generate_originGroup生成初始种群，然后进入双重循环；
对种群的每个个体都计算FCM的目标函数值，计算函数为calculate_goal_value；
对种群进行交叉和变异，ga_cross_and_vary函数生成新种群，计算新种群的目标函数值；
目标函数值如果变小则替换掉父代，否则按照概论决定是否替换；
重复2~4步，遗传若干代后，第二重循环结束，然后更新退火温度，继续第二重循环；
直到退火算法的迭代次数结束，第一重循环结束，整体算法结束。

3.3算法效果

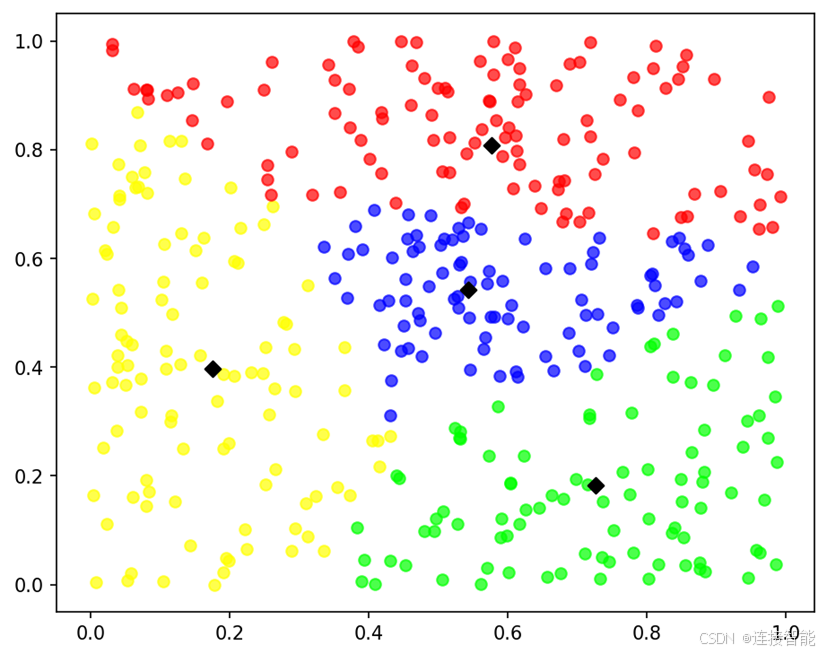
FCM算法目标函数值为3.4635，聚类结果图如下：

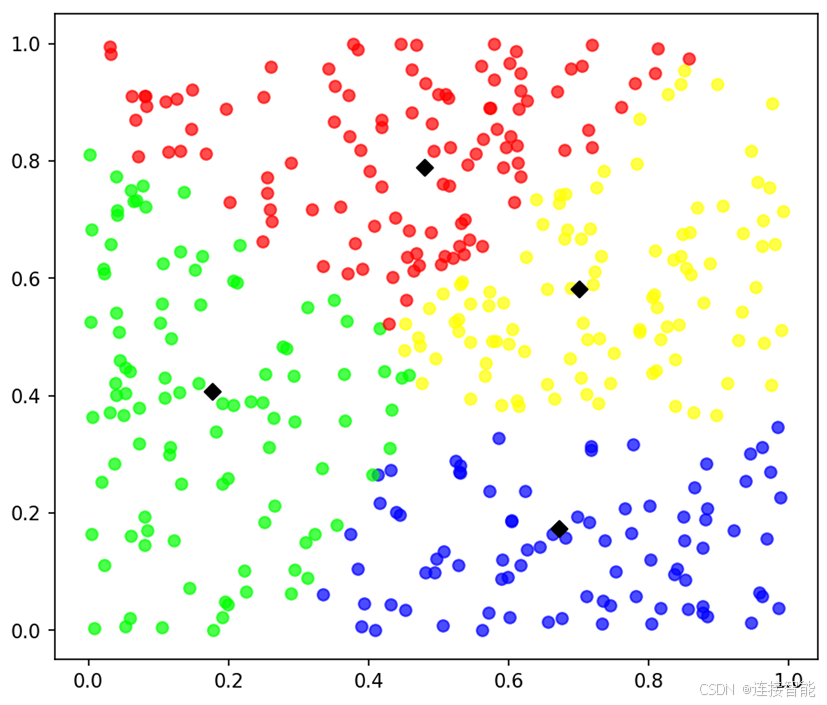
模拟退火加遗传优化FCM算法目标函数值为3.4585，聚类结果图如下：